RF Power Amplifers for Wireless Communications 第一章学习笔记

目录

• 章节导读与精读
• 本章相关公式推导
• 中文参考译文与笔记
• • [1.1 Introduction](#1.1 Introduction)
  • [1.2 Linear RF Amplifier Theory](#1.2 Linear RF Amplifier Theory)
  • [1.3 Weakly Nonlinear Effects: Power and Volterra Series](#1.3 Weakly Nonlinear Effects: Power and Volterra Series)
  • [1.4 Strongly Nonlinear Effects](#1.4 Strongly Nonlinear Effects)
  • [1.5 Nonlinear Device Models for CAD](#1.5 Nonlinear Device Models for CAD)
  • [1.6 Conjugate Match](#1.6 Conjugate Match)
  • [1.7 RF Power Device Technology](#1.7 RF Power Device Technology)
  • 参考文献

章节导读与精读

1.1小节引言部分介绍了功率放大器的定义 ，并提到了功放与一些其他的放大器的相似之处（如设计技术同样适用于接收机前端放大器设计）。随后讲到了功放设计时大多是基于线性放大器的简单拓展和修改，因此引出了线性与非线性的话题 。最后补充一点关于阻抗匹配的差异。

1.2小节是关于线性射频功率放大器理论，从阻抗匹配理论切入，介绍了为什么需要阻抗匹配（寄生电抗影响功率传输）和50Ω标准 。接着讲到晶体管并非理想的单向器件，因此s₁₁和s₂₂需要修正 ，得出新的共轭匹配的计算公式，从中化简出k因子 ，指出二者之间的等价性 。最后补充介绍了一些k因子的理论。

1.3和1.4小节分别是关于弱非线性和强非线性的介绍。其中1.3小节指出一般常用幂级数函数描述弱非线性 。最简单的幂级数没有考虑时间因素，因此提出了 Volterra 级数。当输入小信号，且未接近饱和时，幂级数是比较有效的描述弱非线性的方法 。而当输入信号较大，或者工作在压缩点附近等高驱动水平下时，晶体管表现出了强非线性。1.4小节给出了强非线性效应的定义，并用简单的模型指出了非线性程度。同时表明强弱非线性之间存在一定联系，但是用一个模型描述却存在一定难度。最后用一个简单的例子展示了可以用非线性的模型简单初步计算。

1.5小节介绍放大器晶体管的三种建模方法 ，并讲解不同晶体管更常用的建模思路及原因。随后补充介绍建模时存在的困难 与建模后验证准确性的困难。

1.6小节介绍了负载线匹配理论。指出常见的共轭匹配是基于理想情况的最佳匹配，并未考虑到电压、电流的限制，从而提出了负载线匹配 。随后指出了负载线匹配与VSWR、效率等的关系。

1.7小节介绍了功率放大器相关的发展历程。

本章相关公式推导

另起一篇文章

中文参考译文与笔记

1.1 Introduction

一本关于射频功率放大器（RF Power Amplifier, PA）设计的书，合乎逻辑的起点应该是定义什么是功率放大器。一个技术性的定义可能是：功率放大器是为特定有源器件设计，以实现最大输出功率的放大器。这样的定义很有用，因为它强调了本书中描述的许多技术同样会引起"小信号"放大器设计者的兴趣。例如，在接收机前端的放大器中，同时获得低噪声性能和最大动态范围的问题，也可以被视为 PA 的设计问题，第 2 章中描述的技术同样适用。

但在实际中，当我们说"PA"时，我们真正指的是能对某些东西造成伤害的放大器。我们谈论的是一个射频实验室里"异常刺激"的世界------衰减器和终端会发热，昂贵测试设备的寿命会大幅缩短。这意味着我们讨论的是射频输出从 1 瓦及以上的范围。超过这个水平，即使安全地耗散在衰减器中，我们也能够"感觉到"放大器的射频输出。PA 是那些其输出会直接或间接对人类感官系统产生影响的放大器。

尽管带有"烟火效果"，许多功率放大器设计实际上只是线性放大器设计的简单扩展或修改。因此，首先回顾一下放大器的一般情况，以及线性射频放大器理论中的一些经典结果是很有帮助的。然而，PA 通常工作在有源器件表现出一定程度（甚至是显著程度）的非线性行为下，这使我们立即面临非线性建模和表征的问题。这是一个庞大的主题，近年来已成为数百篇论文和多本书的研究焦点。本书的重点是开发有用、实用的先验设计方法，因此我们将聚焦于基于一些非常基础的模型来发展这些方法，并在全书中持续使用这些模型。这些模型将会在本章的 1.3 和 1.4 节中介绍，并将在那里定义弱非线性和强非线性行为之间的重要区别。

线性射频放大器设计与 PA 设计之间的主要差异之一是：为了获得最佳输出功率，器件的输出端不会呈现线性共轭匹配所要求的阻抗。这往往让人十分困扰，也引发了关于共轭匹配意义及其本质的长期争论。因此，有必要尽早接受这个看似"难以下咽"的结果（在 1.6 节），然后在第 2 章继续对其进行更深入的解释和分析。

1.2 Linear RF Amplifier Theory

关于匹配的双端口线性射频放大器的基本结果最早由 Mason^[1]和 Rollett^[2]推导出来，尽管大多数微波工程师第一次接触这些结果，是在 Bodway 撰写的一份著名应用笔记（"AN-95"）中，这是在早期惠普（Hewlett Packard）的品牌下发布的，目前仍可从 Agilent 获取^[3] 。也有许多介绍基础射频设计技术的书籍对这些内容进行了更详尽的说明^[4] 。

这些关键结果可以通过图 1.1 所示的电路图来说明。一个晶体管被表示为一个双端口 S 参数矩阵。通过概念上的调谐器，可以调节晶体管所看到的输入和输出阻抗（或反射系数）；由于这些调谐器是由无源电路 实现的（例如：传输线、并联电容短截线或 stub），因此在晶体管输入端和输出端参考平面上的反射系数 ΓS 和 ΓL 的幅度都被限制为0 < |ΓS|, |ΓL| < 1。

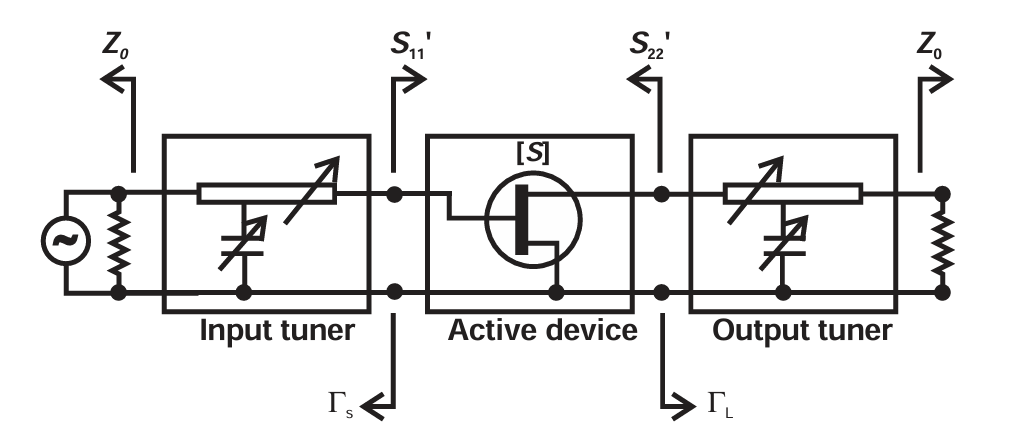
图1.1 Schematic for 2-port gain and stability analysis.

使用调谐器作为获得微波器件有效增益的必要手段，常常让那些在低频领域接受传统"模拟"电子设计训练的工程师感到困惑。同样，图 1.1 中强制假定使用 50Ω 端口这一点，也常成为模拟电路和微波电路之间"派系争论"的焦点。在微波频率下，有源器件通常由于寄生电抗的主导而提供很少有效放大。因此必须花大量精力对这些寄生参数进行谐振补偿，以便在器件的有源节点上建立足够的电压幅度。随着微波器件尺寸和功率能力的增加，这个问题会更加严重。

50Ω 标准的形成有其充分且经过验证的原因，主要与器件间连接导线的寄生效应相关，也与器件到测试仪器之间的寄生效应相关。在 GHz 频段，任何连接导线相对于工作频率的波长而言，其电长度都不可忽略，因此不再能假设连接导线两端的电压相同 。于是，连接导线必须被视为电路设计的一部分，并且必须引入某种形式的物理统一性。传输线以其多种物理形式正满足这种需求，而选择一个标准特征阻抗是必要的。基于我们宇宙中的基本物理常数------特征阻抗低于大约 20Ω 或高于大约 100Ω 的传输线难以制造。过低或过高的阻抗意味着导体间距非常宽或非常窄。因此，介于这些范围之间的任何阻抗都可以作为合理选择。在第二次世界大战前的微波工程开创时期，曾使用过 40Ω 和 80Ω。但真正确立 50Ω 标准的，是微波测试设备产业的发展------像 General Radio 和 Hewlett-Packard 这样的公司在这方面起了主导作用。无论好坏------微波世界围绕着 50Ω 标准运转，而且这种情况似乎不会改变。只需拿一只晶体管，把其输入和输出匹配到 50Ω，你就成为一名微波设计工程师。然而，这条道路上仍存在一些陷阱，主要来自于这样一个事实：晶体管并非完全单向器件，它不仅有正向传输，也存在反向传输。

回到图 1.1，这个系统行为的复杂性很大程度上由反向传输参数 𝑠₁₂ 的相对大小所决定 ；然而，经过较为深入的分析之后，会出现一个更简洁的参数，即 k，或 Rollett 稳定因子。关键方程相当直观，它们表示了由于输出端参考平面所呈现的负载反射系数 Γ𝐿 ，而导致输入反射系数由𝑠₁₁ 变为 𝑠₁₁′ 的变化：

输入匹配：
s 11 ′ = s 11 + s 12 ⋅ s 21 ⋅ Γ L 1 − s 22 ⋅ Γ L ( 1.1 ) s_{11}'=s_{11}+\frac{s_{12}\cdot s_{21}\cdot \Gamma_L}{1-s_{22}\cdot \Gamma_L}\quad(1.1) s11′=s11+1−s22⋅ΓLs12⋅s21⋅ΓL(1.1)

输出匹配：
s 22 ′ = s 22 + s 21 ⋅ s 12 ⋅ Γ S 1 − s 11 ⋅ Γ S ( 1.2 ) s_{22}'=s_{22}+\frac{s_{21}\cdot s_{12}\cdot \Gamma_S}{1-s_{11}\cdot \Gamma_S}\quad(1.2) s22′=s22+1−s11⋅ΓSs21⋅s12⋅ΓS(1.2)

因此，对于共轭匹配，可以设定
s 22 ′ = Γ L ∗ , s 11 ′ = Γ S ∗ s_{22}'=\Gamma_L^*,s_{11}'=\Gamma_S^* s22′=ΓL∗,s11′=ΓS∗

从而得到两个方程，原则上可以解出 Γ𝑆 和 Γ𝐿 。

现在应当注意，一般来说，这个方程组总是存在解的；然而，还存在一个附加约束，即为了使解能够通过外部无源电路实现，ΓS 和 ΓL 的幅度必须小于 1。这正是 k 因子 出现的地方。经过一系列冗长但非常精妙的复数代数推导之后，Rollett 等人证明了满足 0 < |ΓS|, |ΓL| < 1 的条件等价于 一个称为 k 因子的参数大于 1。其定义为
k = 1 − ∣ s 11 ∣ 2 − ∣ s 22 ∣ 2 + ∣ D ∣ 2 2 ⋅ ∣ s 21 ∣ ⋅ ∣ s 12 ∣ k=\frac{1-|s_{11}|^2-|s_{22}|^2+|D|^2}{2\cdot |s_{21}| \cdot |s_{12}|} k=2⋅∣s21∣⋅∣s12∣1−∣s11∣2−∣s22∣2+∣D∣2

以及
D = s 11 ⋅ s 22 − s 12 ⋅ s 21 D=s_{11}\cdot s_{22}-s_{12}\cdot s_{21} D=s11⋅s22−s12⋅s21

因此，从实际意义来看，如果 k > 1，则无论在器件输入或输出端接入怎样的无源匹配网络，该器件的输入或输出反射系数的幅度都不会超过 1。 因此，这个条件对器件的稳定性提出了更进一步的说明。然而，将问题建模为一个双端口网络会引入一些限制，这些限制对于某些应用来说并不够普适，因此文献中一直在追求一套"最终最佳"的绝对稳定性判据，适用于所有条件 ^{[5] [6]}。尽管如此，简单的 k > 1 条件无疑是一个非常好的工程实践指导原则。

不过，这个条件不应被过度延伸。在 PA（功率放大器）设计中，人们经常同时面临获得足够的信号增益和从器件中提取最佳功率这两个困难。这通常是成本驱动的设计趋势所导致的：大结型面积的晶体管通常增益较低，而设计中往往受到使用低成本工艺的限制。稍后我们会看到，当信号增益下降到 10 dB 以下时，为补偿增益而增加的额外射频驱动功率往往会抵消掉精心设计的效率优势。其结果是人们通常希望 k 因子大于 1，但不要过大 。具有较高 k 因子的器件往往增益较低，而通过允许器件内部存在一定正反馈（同时仍保持 k > 1），可以"取回"一些增益。这个技巧在微波 ECM 放大器和毫米波放大器社区中常被使用，有时甚至是无意中使用的；它也是二战前电子管无线电行业的主要技术之一，包括所谓的"再生"调节。

如果 k > 1，文献中给出了共轭匹配及对应的最大可用增益（MAG, maximum available gain）的表达式。这些表达式非常常见，此处不再重复^{[3] [4]}。但仍有一些值得注意的影响：

1. k 稍大于 1 的器件，其增益/匹配特性比理论上的单向器件更激进。特别地，最终的 MAG（在近似匹配条件下）可能比单纯根据 VSWR（电压驻波比）失配计算所得的要高得多。例如，一个器件的回波损耗为 10 dB 时，在更优匹配到 −20 dB 的回波损耗后，其增益可能增加超过简单计算得到的 0.7 dB。

2. 电路损耗会严重影响 k 因子，尤其影响其跨越 1 的频率点。在实际中，如果 k 因子是基于完全去嵌的 S 参数测量结果，则器件在 k < 1 的一定频率范围内仍然可以安全使用。

3. 晶体管所处的电路环境会显著改变其有效 S 参数，尤其是关键的反向传输参数 s₁₂。这可能是导致意外或模拟器无法复现的稳定性问题的主要原因。

4. 经典形式的 k 因子分析仅适用于单级放大器。在多级放大器中，中间级的输入端或输出端由有源网络终端，因此不再满足 0 < |ΓS|, |ΓL| < 1。

   因此，将整个多级放大器视为单一双端口并计算其 k 因子，只是稳定性的必要条件，但远非充分条件。在多级射频放大器设计中，人们通常通过在级间加入某种形式的隔离来绕过这个问题，尽管也已有文献提出多级稳定性分析和设计策略^[7]。

1.3 Weakly Nonlinear Effects: Power and Volterra Series

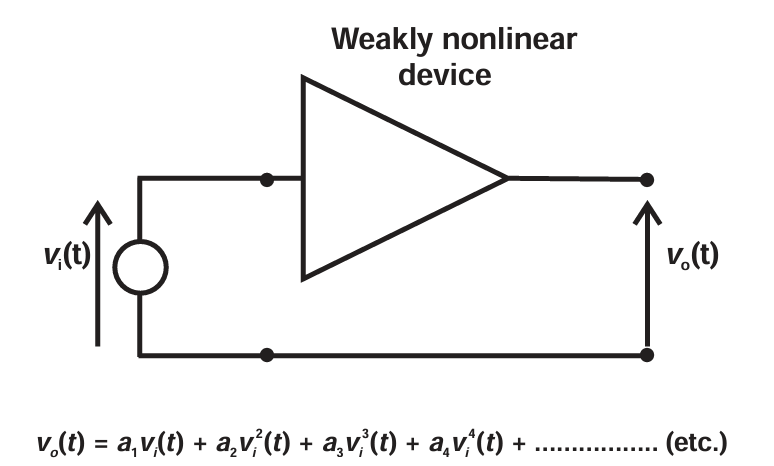
图1.2 Weakly nonlinear device, and power series.

在线性放大器中可能出现的非线性效应通常首先以幂级数表达式的形式引入，如图 1.2 所示。

图中的放大器符号代表晶体管及其相关的输入和输出匹配电路，而小写电压量表示晶体管工作点附近的射频小信号变化。放大器的输出包含一个无限项的非线性产物级数，这些项叠加在线性增益所代表的第一项之上：
v o = a 1 v i + a 2 v i 2 + a 3 v i 3 + a 4 v i 4 + ... ... ( 1.3 ) v_o=a_1v_i+a_2v_i^2+a_3v_i^3+a_4v_i^4+......\quad (1.3) vo=a1vi+a2vi2+a3vi3+a4vi4+......(1.3)

这种"幂级数"在许多基础教科书中被当作非线性行为的通用表达式；但它显然存在局限性。最显著的是，它（幂级数表达式）没有考虑输出各成分的时间因素 。我们知道，即使图 1.2 中的放大器图标内容只是一个无源 R--C 网络，输出电压也会相对于输入信号发生幅度和时间（相位）变化。一种更强大的幂级数形式称为 Volterra 级数，它能够包含相位效应。尽管如此，幂级数在描述晶体管直流工作点附近的小范围操作区内的非线性产物行为时仍然具有实用价值。进一步的局限性在于幂级数中的系数 a_n 对输入与输出调谐状态、以及输入与输出偏置电平高度敏感。

通过一定改进，这种表述可用于分析放大器或器件的"弱非线性"特性。例如，输入信号的互调失真低于 −30 dBc²。这些低电平非线性难以通过基于 I--V 曲线拟合的模型准确预测，因此直接测量幂级数参数，可作为预测弱非线性的途径。这种方法（在更强大的 Volterra 级数框架下）已被 Maas ^[8] 深入研究，对于接收机组件设计非常重要，因为系统规格对低至 −100 dBc 的非线性产物仍然敏感。

总体来说，PA 在 1 dB 压缩点附近或更高驱动水平下需要更加谨慎的处理，因为其非线性变得强，主要源自晶体管的截止与削波行为 。尤其要注意只截断到二阶或三阶项的幂级数分析方法。在小信号放大器中，三阶非线性无疑在压缩和饱和效应中非常关键；但在功率放大器中，当逼近 1 dB 压缩点时，五阶与七阶项开始变得显著，并在高驱动时占主导。

1.4 Strongly Nonlinear Effects

强非线性效应是指由于晶体管的极限工作状态而引起的信号波形失真 。这一点可以通过一个简单的、理想化的场效应晶体管（FET）转移特性（如图 1.3 所示）来说明。当栅源电压使沟道完全关闭时，漏极电流会出现截止；而当达到开沟道状态时，进一步增加栅源电压，对漏极电流的增加已经几乎没有作用。图 1.3 所示的特性是高度理想化的，无论是截止和饱和的突变程度，还是中间区域的完全线性化表现，都与实际情况差距甚大。我们将这种模型称为理想强非线性模型。尽管它明显非常理想化，但它在教材中被广泛用于推导功率放大器（PA）的输出功率和效率公式。

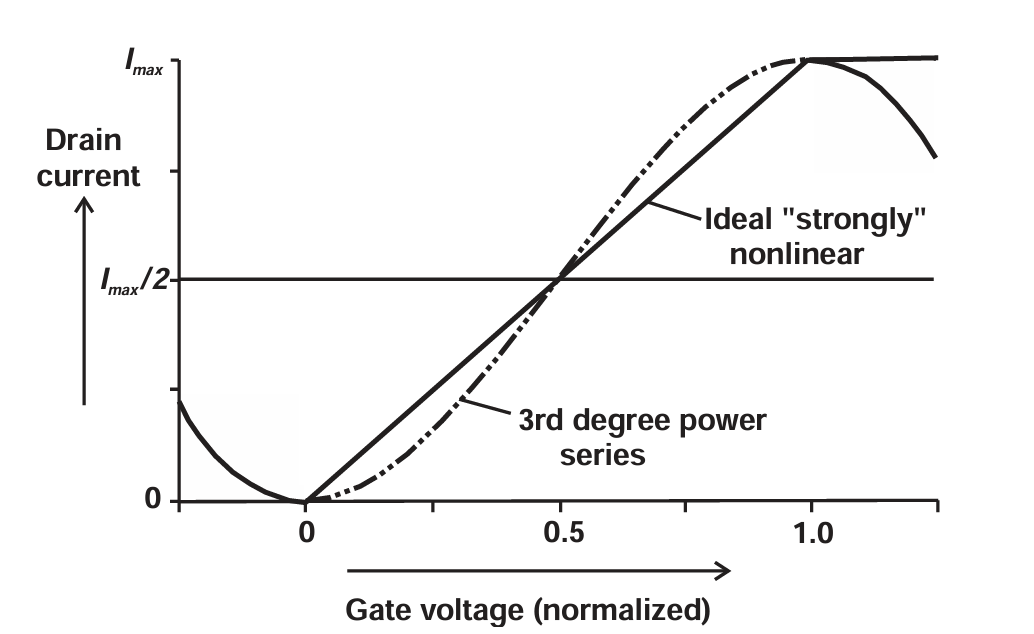
图1.3 FET transfer characteristic, showing attempts to model weakly nonlinear (dotted) and

strongly nonlinear (solid) effects.

图 1.3 中的虚线显示了一个更接近真实的 FET 转移特性。可以看到截止更为平滑，在接近最终截止点时跨导逐渐"衰减"；进入饱和区时，特性也同样平滑地接近开沟道状态。尝试用数学方式对这条曲线建模是很有意义的，因为这样可以迅速看出强非线性与弱非线性的区别，并体验到用同一个模型同时满足两者的困难。

跨导衰减在许多类型的 FET 中都非常典型，且通常近似呈平方律行为。而限制特性则可被视为三阶效应。因此，一个形式如下的方程：
I d = g 0 + g 1 ⋅ V g + g 2 ⋅ V g 2 + g 3 ⋅ V g 3 ( 1.4 ) I_d=g_0+g_1\cdot V_g+g_2\cdot V_g^2+g_3\cdot V_g^3\quad(1.4) Id=g0+g1⋅Vg+g2⋅Vg2+g3⋅Vg3(1.4)

将具有这些特性中的部分。如果我们把在截止与饱和之间的栅压归一化到 0 到 1 的范围，可以推导得到一个合适的表达式
I d = + 3 ⋅ V g 2 − 2 ⋅ V g 3 ( 1.5 ) I_d=+3\cdot V_g^2-2\cdot V_g^3\quad(1.5) Id=+3⋅Vg2−2⋅Vg3(1.5)

需要注意，这个方程并不是一个严格意义上的幂级数；它试图在整个工作区间上模拟晶体管的转移特性。表面上缺少线性项看起来有些奇怪，但稍后会对此进行解释。事实上，图 1.3 中虚线部分的曲线就是根据这个方程在截止与饱和之间绘出的。在该范围外，简单的三次方程无法表现硬饱和和完全截止的行为，因此仿真器需要另行处理。在这些强非线性区域，要建模其行为，必须在式（1.4）中加入更多高阶项。另一种方法，则是在弱非线性模型上加上硬饱和与硬截止的条件，通过合适的 if 判断实现。这种效果示于图 1.4。使用计算机绘制曲线和计算方程时这相当容易实现，但它已经偏离了简单的解析方法。尽管如此，本书将不时使用这种"强-弱混合"模型，以使模型比图 1.3 中的理想强非线性模型更贴近真实，又不会丢失解析可处理性。

图1.4 Combined weak and strong nonlinear model.

将这里的讨论与弱非线性效应联系起来也很有意义。我们可以取式（1.5）中的特性，并在某个选定偏置点展开幂级数，提取幂级数系数。

将V_g=V_b+v_s(t)代入(1.4)中，可得：
i D ( t ) = 3 ( V b + v s ( t ) ) 2 − 2 ( V b + v s ( t ) ) 3 = ( 3 V b 2 − 2 V b 3 ) + ( 6 V b − 6 V b 2 ) ⋅ v s ( t ) + ( 3 − 6 V b ) ⋅ v s 2 ( t ) + ( − 2 ) ⋅ v s 3 ( t ) ( 1.6 ) i_D(t)=3(V_b+v_s(t))^2-2(V_b+v_s(t))^3 =(3V_b^2-2V_b^3) +(6V_b-6V_b^2)\cdot v_s(t) +(3-6V_b)\cdot v_s^2(t) +(-2)\cdot v_s^3(t)\quad(1.6) iD(t)=3(Vb+vs(t))2−2(Vb+vs(t))3=(3Vb2−2Vb3)+(6Vb−6Vb2)⋅vs(t)+(3−6Vb)⋅vs2(t)+(−2)⋅vs3(t)(1.6)

因此，通过比较式（1.6）中 v_sⁿ(t) 的系数与式（1.3）中的幂级数表达，可以得到：
a 1 = ( 6 V b − 6 V b 2 ) a 2 = ( 3 − 6 V b ) a 3 = ( − 2 ) a_1=(6V_b-6V_b^2) \\a_2=(3-6V_b) \\a_3=(-2) a1=(6Vb−6Vb2)a2=(3−6Vb)a3=(−2)

从这些幂级数系数 a_n 中可以得出一些有用且更一般性的结论：

1. 小信号增益 a₁ 是直流偏置电压 V_b 的强函数。
2. 二阶非线性 a₂ 在 V_b = 0.5 时穿过零点并改变符号。这意味着在 V_b = 0.5 偏置点附近不会产生二次互调成分。在更高阶的系统（更符合真实器件）中，类似的"零点"可能出现在所有阶数的非线性系数中。这些零点或"甜点"在真实器件中非常常见，它们是曲线几何特性（如拐点）的自然结果，因此无需从器件物理进行解释。
3. 三阶非线性 a₃ 为常数（因为我们只取三阶幂级数）。在真实器件中，它应该随偏置变化，但其负号表明器件会出现限制行为，从而模拟器件在接近饱和区时的"压缩"效应。

1.5 Nonlinear Device Models for CAD

为了对器件建立一个全面的模型，显然必须同时刻画其弱非线性和强非线性行为。不幸的是，在具体器件中，这两类非线性源于完全不同的物理机制。这对器件建模者乃至最终使用者都构成挑战，因为至今仍难以获得完美的模型。更糟糕的是，功率放大器（PA）设计者对常用 CAD 模型缺陷的敏感程度，远高于许多其他 RF 器件的设计者。这一点在 RF 功率 BJT、MOSFET 以及近年的 MESFET 和 HBT 中都同样成立，尽管后两者在技术期刊和研讨会中获得了更多关注。

用于 CAD 的器件建模大致分为三类：

• 物理模型（Physical models）：从"自底向上"模拟器件物理和制造几何结构；

• 等效电路模型（Equivalent circuit models）：将器件物理行为转换为等效的电路元件；

• 行为模型（Behavioral models）：基于三端 DC 测量特性，拟合得到抽象数学方程。

一般而言，大多数 RF CAD 器件模型采用第二类（等效电路模型），并辅以第一类或第三类技术。BJT 建模历史上主要走物理模型路线，而现有 FET 模型更多体现"自顶向下"的方法。这可能源于两者工作原理的差异。即便在最简化的形式下，场效应器件中的电场分布与耗尽区形状的精确求解也是一个复杂的静电学问题；反之，BJT 和半导体结的量子力学虽然看似更复杂，却能推导出可处理的 I--V 数学表达式，并成为当今 CAD 软件中 BJT 模型的基础。商业 CAD 软件中使用的模型通常最终都表现为一个包含大量线性元件以及一些非线性元件的等效电路 。部分元件对应物理结构，但许多元素是经验加入的，以便更好地拟合测量结果。最大的问题之一在于：这些模型中的若干元件参数是耦合的（coupled），由于模型是经验而非物理驱动的，这会使得工艺波动和良率分析非常困难------任何设备参数的物理变化可能要求同时修改多项甚至全部等效参数。

近年来，第三类行为模型得到了更多关注。曾经有人认为，不可能仅用端口电压和电流构造一个能完整描述非线性器件的数学函数。然而，一些新的研究成果显示，行为建模在未来可能产生重大影响 ^[9]。

RF 功率器件建模的核心难题是缩放 。几乎所有情况下，详细建模是在一个尺寸远小于实际功率器件的"单元管"上完成的。单元模型可能非常准确。模拟 IC 和高频接收组件的设计者通常可以使用这些模型来获得与仿真几乎一致、表现优异的性能。但是对于功率放大器而言，设计者必须将这种小单元扩大几十倍甚至几百倍，以"组合"出一个功率晶体管。缩放过程并不是简单的电节点扩展，这在现代仿真器中并不困难，而是会引入许多单元模型中可以忽略但在大器件中非常显著的二次现象。例如，非均匀热效应会破坏"所有单元电流、电压一致"的假设。多个并联导致的极低阻抗会引发更多以前可忽略的行为，如焊线接触处的电流扩散、晶体中的电-声耦合、焊线之间的互耦等等。

也许大规模射频功率晶体管模型不充分的最隐蔽方面是，很难通过简单的对比测试来检验模型与器件 。即便是基本的 I--V 测量，对 RF 大功率晶体管来说也有极大困难。大多数实验室 I--V 曲线测试仪的速度比 RF 信号慢数个数量级，慢到会引入瞬态结温效应，而这些效应在真实 RF 周期内几乎不会出现 。这还假设测试仪能提供数安电流，并且电压、电流传感器已补偿引线压降。另一个常见问题是振荡。大尺寸 RF 器件在低频稳定性方面常出现问题，在 I--V 曲线上表现为"折点"，甚至混沌吸引子式的螺旋状轨迹 。本书后面将讨论抑制振荡的方法，但这些方法用于 I--V 测试时效果有限，因为测试夹具中不可避免的高值退耦电容会改变 I--V 曲线。有些 I--V "环形"曲线确实源于器件固有行为，但也可能由测试夹具的退耦造成。

对于射频功率晶体管来说，要获得准确的 I-V 曲线是很困难的 。因此，许多研究者搭建定制测试平台，通常采用脉冲测量方法 ^[10]。另一种方法是构建能以 RF 速度扫描 I--V 的曲线测试仪 ^[11]。这两种方式都面临快速、高精度电压与电流测量的挑战。通常，从这些装置获得的 I--V 曲线与普通低频曲线测试仪得到的曲线很不相同，这也对仅基于 DC 测量进行曲线拟合提出了重大质疑。DC 与 RF I--V 曲线不一致在微波 GaAs MESFET 中已有大量研究，但在较低频段的 Si BJT 与 MOSFET 中关注较少。虽然从物理角度看 BJT 可能较不敏感，但仍值得进一步研究。

测量问题不仅限于 I--V；S 参数的测量同样困难。RF 功率器件的阻抗通常非常低，与 50 Ω 参考相比低得多，使得简单的线性 S 参数测量也会遇到校准困难。常见（但不可靠）的方法是测量更小的单元并进行缩放。另一种方式是将预匹配网络紧贴大器件加上，使阻抗变换至可测范围，但随后 de-embedding 校准问题同样严峻。逐渐地，人们认识到：得到准确 RF 功率晶体管模型的最好方式是直接构建放大器------甚至是非优化的设计------并将电路与器件模型一起拟合至测量结果。

关于这些问题的文献很丰富，超出本书范围。参考文献 ^[12--16] 提供了一个起点，但研究仍在继续，相关论文在国际会议上仍占据多个分会场。显然，一些拥有充分时间与设备的团队已经能够解决特定产品的 PA 仿真所需的大部分模型问题，但他们的成果往往不会公开，也不会进入商业 CAD 模型库。虽然 GaAs RFIC 代工厂的客户可能获得较好的工艺模型，但封装 RF 功率晶体管在商业模型数据库中往往较差。因此，工程师常常只能尽可能使用可获得的模型，甚至基于通用模板自行构建。这种不理想的状况，使许多从业者不得不回到传统的反复试验设计方法。本书希望展示CAD 工具在 RF 功率放大器设计中具有重要价值，并鼓励将传统方法与现代技术结合使用。

1.6 Conjugate Match

共轭匹配的概念在 1.2 节已经使用过，似乎无需进一步解释。一个如图 1.5 所示的信号源，当外接负载电阻等于信号源阻抗的实部（并假设所有可调谐的无功部分都已谐振掉）时，将向外部负载传递最大功率。这个基本结果看似无需重复讨论，但当理想信号源被真实器件替代，尤其当信号源是晶体管的输出电流源时，会出现一个必须谨慎避免的陷阱。

图1.5 Conjugate match and loadline match.

简单证明中，信号源被证明在可变负载电阻上提供最大功率，但这个证明完全没有考虑信号源可能存在的物理限制，包括它能够提供的最大电流，以及（尤其是）其端口所能承受的最大电压 。例如，一个电流源的最大电流为 1 A，输出电阻为 100 Ω。根据共轭匹配定理，应选择 100 Ω 的负载以获得最大功率。但此时电流源端电压为 50 V。如果该电流源是晶体管的输出，这个电压很可能超过器件的额定耐压。此外，晶体管的电压摆幅也受限于可用的直流供电电压。

因此，对于只能观察到负载电阻中功率（但看不到电压或电流波形）的外部观察者来说，该器件会在远低于物理最大电流 I_max 的情况下出现限制行为 （见图 1.5）。这显然是不可取的，晶体管没有被充分利用，不能发挥其最大能力或"效用"。为了利用晶体管的最大电流和电压摆幅，需要选择更低的负载电阻；这个值通常称为"负载线匹配"，记作 R_opt，在最简单形式下等于
R o p t = V m a x / I m a x R_{opt}=V_{max}/I_{max} Ropt=Vmax/Imax

在假设 R_gen >> R_opt 的前提下成立；如果考虑 R_gen，则需要解方程：
R g e n ⋅ R o p t R g e n + R o p t = V m a x I m a x \frac{R_{gen}\cdot R_{opt}}{R_{gen}+R_{opt}}=\frac{V_{max}}{I_{max}} Rgen+RoptRgen⋅Ropt=ImaxVmax

本节讨论的两个结果------共轭匹配与负载线匹配------都是电子学中最基础的结果。然而，当它们在射频环境中同时出现时，许多人会认为它们互相矛盾。关于这种"矛盾"的讨论，以及可能的解决方法，是一些技术杂志与业余无线电期刊通信栏目中的热门话题。关键问题在于问题陈述方式。基本的共轭匹配定理仅适用于电流、电压无限制的理想情况；而负载线匹配是现实中的折衷，为了从射频晶体管中提取最大功率，同时确保射频电压摆幅不超过器件极限或可用直流供电电压。

尽管如此，争议仍然持续。例如常有人断言，使用负载线匹配而非共轭匹配的晶体管会在其连接的系统中引发反射和 VSWR问题。然而，这只是一半的真相，**只要 PA看到合适的负载，它本身就能正常工作，无论系统中负载环境是什么样。**另一面却是，PA 输出所连接的系统组件，很可能将面对一个不同于其规范要求的输入终端条件。于是问题出现，也许这就是问题的核心：PA 的输出阻抗到底是多少？如前所述，负载线匹配的原因是为了容纳晶体管的最大电流和电压摆幅。这与器件的阻抗无关，而器件阻抗在其线性范围内可认为大致恒定。

一个工作在 A 类的器件，没有进入截止或饱和区间，将向外呈现接近其小信号输出阻抗（S22 参数）的特性。在这种情况下，PA 基本遵循线性级联规则，可追溯到戴维宁（Thevenin）定理。但一旦器件开始工作在明显非线性区域，即使仅占 RF 周期的一小部分，输出阻抗的概念就开始失效，因为波形不再是正弦波 。例如，在第 3 章我们将介绍"降低导通角"的 AB 类放大器。在这种广泛使用的 PA 工作模式中，输入射频电压会使器件进入完全截止、无电流流动的区域。在这种状态下，根据定义，器件向外呈现开路。这样一台放大器，其瞬时输出阻抗呈现一种开关特性，如图 1.6 所示。戴维宁在提出他的定理时可没有考虑过这种器件。如果他知道电气工程专业学生被如此严苛地反复灌输他的定律，他一定会感到担忧。在实际电子系统中存在着大量戴维宁定理根本不适用的场景。

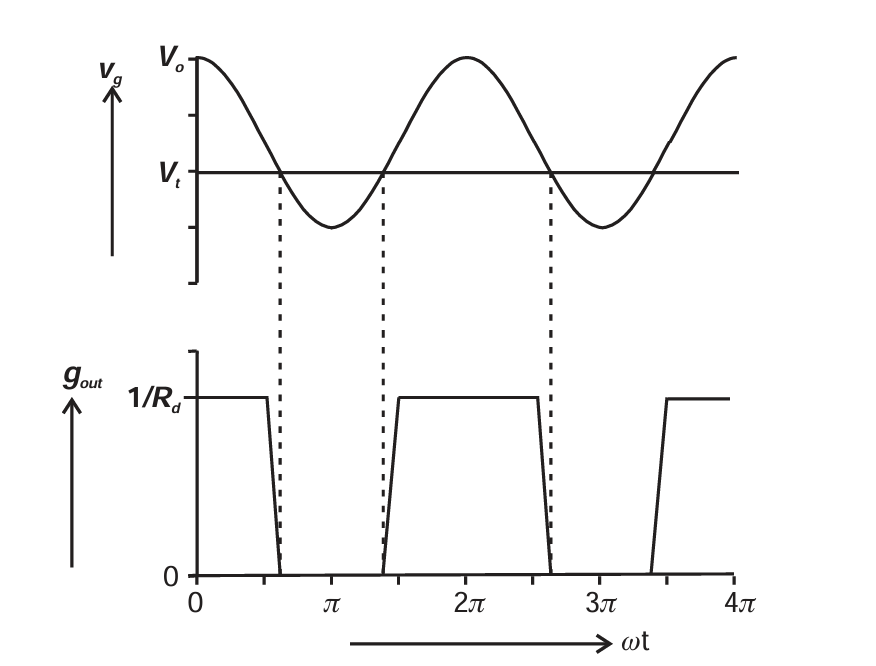
图1.6 Output conductance variation of device in Class AB (output parasitic reactances ignored).

这不禁让人想起诺贝尔奖得主、物理学家费曼关于电工学中复阻抗的评论：

（费曼引文略）

但费曼不满的，仅仅是将欧姆定律扩展到包含交流系统中的复阻抗。他若看到有人试图用戴维宁定理去表示如图 1.6 所示的明显非线性器件，恐怕会更加震惊。这类理想化的符号化处理，看起来确实带有一种"为了让方程形式看起来更像以前学的内容，而不顾适用范围"的味道。我们习惯将戴维宁导纳称为器件的"输出导纳"。尽管它是一个行为性的，而非物理性的参数，但随着时间推移，我们似乎把它从概念性的参数演变成了物理实体。然而，对于图 1.6 这样的器件，必须在其期望的外部环境下进行测量，然后可能才能确定一个更全局的行为模型，但这样的模型绝不会是一个简单的戴维宁等效模型。

工程师的时间和注意力都是有限的，无法过多纠结于哲学或语义问题。高度非线性的 PA 输出级通常通过隔离器或平衡结构（见第 13 章）与外部世界连接，这是简单有效的解决方案。

1.7 RF Power Device Technology

最初，只有硅（Si）；后来砷化镓（GaAs）出现了。硅便宜，GaAs昂贵，但在 2 GHz 以上的频率，GaAs 很快便占领了微波领域。其最初主要应用于低噪声接收器件。尽管 GaAs 存在一些严重的材料和可靠性问题（花了十几年才解决），但最终仍然实现了数十瓦级的高功率器件。进入新千年后，事情开始变得更复杂。无线通信领域对超大规模消费类产品提出了低成本要求，因此需要更便宜的半导体技术，硅技术重新开始回潮。高功率应用（尤其是 830 MHz 与 2 GHz 的蜂窝基站功放）成为了新型硅技术的理想目标------这种硅技术虽无法在高 GHz 的军事和卫星通信中与 GaAs 竞争，但在 2 GHz 附近能以更低成本提供相近性能。这种技术由摩托罗拉最初开发，是长期使用的射频 MOS（金属氧化物半导体）工艺的衍生技术，被称为 横向扩散金属氧化物半导体（LDMOS）。LDMOS 已成为 2 GHz 以下任何高功率功放的默认选择，并几乎彻底消灭了射频功率硅双极器件产业（除了仍为特殊应用或长期合同生产少量器件的厂家）。

与此同时，GaAs 技术则以一种意想不到的形式发展------异质结双极晶体管（HBT），并成为低功率手机功放的主流技术。这是 GaAs 技术的另一条令人意外的发展路径，建立在至少 20 年颇具可靠性问题的 HBT 研究基础上。手机应用青睐只需单电源并能完全关断的器件，而这使得 HBT 成为"必选"技术，尽管其在更高功率应用中的推广仍较缓慢。

当下 GHz 射频功率技术中最重要的发展，是宽禁带半导体的崛起，它们从研究实验室走向了商业。尽管碳化硅（SiC）曾长期被视为最具潜力的候选者，但它已被 2000 年代新的"神奇材料"------氮化镓（GaN） 所超越。这种技术带给射频功率领域的关键优势是：高电压操作能力。能够在 100 V 电压下运行的 GaN 器件已开始面市，其外围功率密度可达到 GaAs 的五倍，且阻抗水平高出一个数量级。虽然此类技术最直接的应用（也是多数开发资金来源）是宽带军事电子对抗系统（ECM），但第三代（3G）移动通信系统快速增长的功率需求也使得 GaN 的吸引力与日俱增。至少可以说，过去对"电子真空管技术复兴"的预测似乎有点偏离目标了。

参考文献

1\] Mason, S., "Power Gain in Feedback Amplifiers," IRE Trans. Circuit Theory, CT-1, June 1954, pp. 20--25. \[2\] Rollett, J. M., "Stability and Power-Gain Invariants of Linear Twoports," IRE Trans. on Circuit Theory, March 1962, pp. 29--32. \[3\] Bodway, G., "S-Parameters, Circuit Analysis and Design," Hewlett Packard Application Note AN95. \[4\] Vendelin, G., A. Pavio, and U. Rhode, Microwave Circuit Design, New York: Wiley, 1990. \[5\] Woods, D., "Reappraisal of the Unconditional Stability Criteria for Active 2-Port Networks in Terms of S-Parameters," IEEE Trans. Circuits Syst., CAS-23, February 1976, pp. 73--81. \[6\] Gupta, M.S., "Power Gain in Feedback Amplifiers, A Classic Revisited," IEEE Trans. Microwave Theory \& Tech., MTT-40, May 1992, pp. 864--879. \[7\] Macchiarella, G., et al., "Design Criteria for Multistage Microwave Amplifiers with Match Requirements at Input and Output," IEEE Trans. Microwave Theory \& Tech., MTT-41, August 1993, pp. 1294--1298. \[8\] Maas, S., Nonlinear Microwave Circuits, Norwood, MA: Artech House, 1988. \[9\] Wood, J., and D. E. Root, (eds.), Fundamentals of Nonlinear Behavioral Modeling for RF and Microwave Design, Norwood, MA: Artech House, 2005. \[10\] Barton, T., et al., "Narrow Pulse Measurement of Drain Characteristics of GaAs MESFETs," Elect. Lett., Vol. 23, No. 13, June 1987, pp. 686--687. \[11\] Smith, M., et al., "RF Nonlinear Device Characterization Yields Improved Modelling Accuracy," Proc. IEEE Intl. Microw. Symp., MTT-S, 1986, pp. 381--384. \[12\] Snowden, C., and R. Miles, (eds.), Compound Semiconductor Device Modelling, New York: Springer-Verlag, 1993. \[13\] Seitchik, J. A., C. Machala, and P. Yang, "The Determination of Spice Gummel-Poon Parameters by a Merged Optimization-Extraction Process," Bipolar and Circuits Technology Meeting, 1989, pp. 275--278. \[14\] Statz, H., et al., "GaAsFET Device and Circuit Simulation in Spice," IEEE Trans. Electron Devices, ED-34, February 1987, pp. 160--169. \[15\] McCamant, A., G. McCormack, and D. H. Smith, "An Improved GaAs MESFET Model for Spice," IEEE Trans. Microwave Theory \& Tech., MTT-38, June 1990, pp. 822--824. \[16\] Root, D., and B. Hughes, "Principles of Nonlinear Active Device Modelling for Circuit Simulation," Proc. IEEE MTT ARFTG Conf., Tempe, AZ, 1988, pp. 3--26.