【读论文】非线性交叉克尔准经典动力学

目录

摘要

[1. 引言](#1. 引言)

[2. 交叉克尔准经典演化](#2. 交叉克尔准经典演化)

[3. 模式关联动力学](#3. 模式关联动力学)

[4. 偏振压缩](#4. 偏振压缩)

[5. 动力学在球面上的映射](#5. 动力学在球面上的映射)

[6. 耗散效应](#6. 耗散效应)

[7. 结论](#7. 结论)

致谢

[附录 A. 双模维格纳函数](#附录 A. 双模维格纳函数)

[附录 B. 约化密度矩阵的纯度](#附录 B. 约化密度矩阵的纯度)

参考文献

摘要

本文研究了交叉克尔效应的准经典动力学特性。在该近似条件下，两种偏振模式之间退相干的典型周期性复苏现象消失，且模式保持纠缠状态 。通过将动力学过程映射到庞加莱空间，我们得到了偏振压缩的简单条件。当考虑耗散效应时，态在该空间中的形状未发生显著改变，但其尺寸有所减小。

1. 引言

光学克尔效应指的是光场在三阶非线性介质中传播时，所经历的强度相关相移 现象。这一效应会产生显著的非高斯操作，由于其在量子非破坏测量 [1-9]、量子叠加态产生 [10-19]、量子隐形传态 [20-22]、量子逻辑 [23-28] 以及单粒子探测器 [29-31] 等多个领域具有潜在应用价值，因而引发了广泛关注。

在电磁感应透明 [32-35]、玻色 - 爱因斯坦凝聚体 [36]、冷原子 [37] 以及约瑟夫森结 [38-40] 等体系中，已观测到增强的克尔非线性效应。其他相关实验装置还包括利用珀塞尔效应 [41]、里德伯原子 [42]、光致斯塔克位移 [43] 以及纳米机械谐振器 [44] 等。

值得特别关注的是，这种三阶非线性在压缩光产生过程中所发挥的重要作用。早期的相关方案包括采用非线性干涉仪 [45] 或简并四波混频 [46,47] 等。但不久之后，光纤便成为了产生压缩光的典型载体 [48-53]。然而，由于石英玻璃中的非线性效应通常较为微弱 [54]，基于克尔效应的光纤需要较长的传播距离和较高的功率，这也随之带来了其他一些不期望出现的效应 [55,56]。

本文将重点关注高强度极限情况 ，在这一情况下，经典描述有望适用。在合理的假设条件下，麦克斯韦方程组可推导出一组耦合非线性薛定谔方程，该方程长期以来一直是描述非线性色散介质中光场行为的有效工具。它已成功用于解释脉冲压缩、暗孤子形成以及超短脉冲自聚焦等多种不同现象 [57]。然而，仍有一些非经典特性无法通过这种经典方式来解释。换句话说，在最基本的层面上，光在克尔介质中的传播必然伴随着量子效应。

综上所述，我们所希望探索的这一体系处于经典世界与量子世界的边界。或许，利用相空间 方法 [58-60] 能够最好地研究这两个世界之间的过渡。这使得我们有可能通过准经典描述来获取一些关于非经典行为的信息，该描述主要采用经典轨迹，同时通过维格纳函数等工具 [61-63] 考虑正确的量子初始态 。尽管在解释方面存在一些问题，但维格纳函数已在物理学的多个领域受到了广泛关注 [64]，并且已经被应用于量子光学中的一些非线性问题 [65-69]。

折射率的强度依赖性是克尔效应的显著特征，其主要通过两种方式体现：自相位调制和交叉相位调制。自相位调制指的是光场在传播过程中所经历的自诱导相移，而交叉相位调制则是指由另一个具有不同波长、传播方向或偏振态的光场所引起的非线性相移。

本文聚焦于交叉克尔效应，因为它与实现偏振压缩密切相关，而偏振压缩 是我们实验室的一个主要研究目标 [70]。我们利用准经典 方法，以简洁的方式重新分析了该情况下的光传播过程：在忽略高阶涨落之后，我们得到了维格纳函数的演化方程，并能够将其积分为解析形式 。这使我们能够研究模式关联的动力学特性。由于得到的态是非高斯的 ，常用的纠缠判据 [71,72] 的应用变得较为困难，因此我们转而研究约化态的纯度，这一研究可以通过封闭形式进行。

双模维格纳函数可以根据相空间形式的斯托克斯参数 恰当地表示在庞加莱空间 中，从而提供直观的物理图像。最后，由于克尔动力学过程是光子数守恒的，基于将模式耦合到有损耗库的标准耗散模型 [73] 似乎并不适用。相反，我们考虑了通过纯退相过程实现的耗散，这一过程恰好是可解的。结果表明，维格纳函数的形状未发生显著改变，但其尺寸有所缩小。

2. 交叉克尔准经典演化

如第 1 节所述，交叉克尔构型对应的情况是：一束光（例如 a 光束）的折射率会受到另一束光（例如 b 光束）强度的调制 。这些光束在两个正交偏振模式中激发，在量子描述中，这两个模式由两个复振幅算子a^和b^表征。这些算子满足标准的玻色子对易关系：
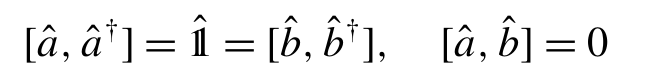中间的这个符号是 hat 1？

(2.1)

其中上标†表示伴随算子。

利用这些湮灭算子和产生算子，描述交叉克尔相互作用的哈密顿量为 [74]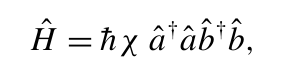：（2.2）

其中χ是与三阶非线性极化率相关的有效耦合常数。

对于由密度算子ρ^​描述的任意态，其演化满足：

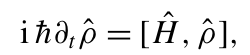（2.3）

其形式解可表示为：

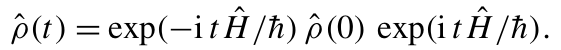(2.4)

通过在双模福克基矢∣na​,nb​⟩中展开该方程，原则上可以追踪态的演化过程。以初始纯双模相干态∣Ψ(0) ⟩=∣α0​,β0​⟩为例（此后下标 0 表示相应变量在t=0时的值），演化后的态为：

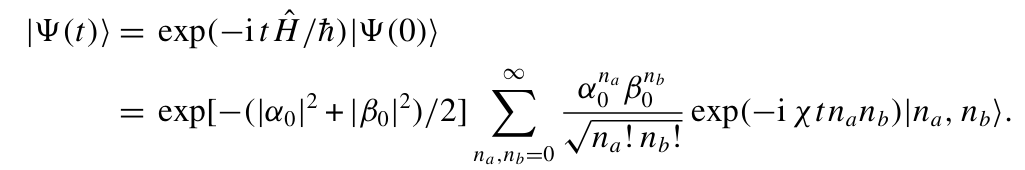(2.5)​

项exp(−iχtna​nb​)源于模式之间的耦合 ，导致该态无法分解为单模态，也就是说，如我们将在下一节中详细探讨的，该态会变得纠缠。

显然，方程 (2.5) 仅对少光子态具有实际应用价值。实际上，这种精确解无法以直观的形式提取出动力学的经典部分。为此，我们将模式算子a^和b^分解为：

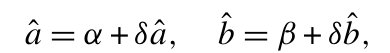(2.6)

即经典振幅 与量子噪声算子 之和。假设噪声算子的平均值远小于相应的相干振幅 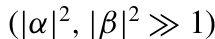，因此我们可以将分析限制在δa和δb的一阶项 。如果我们采用双模维格纳函数W(α,β) 以及附录 A 中概述的基本方法，结合这种线性化近似，方程 (2.4) 可以重新表示为：

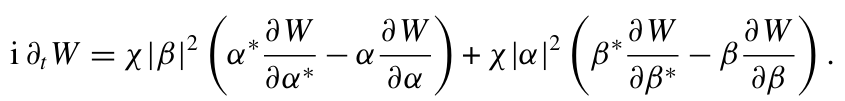(2.7)

在此需要说明两点。首先，由于我们忽略了噪声算子的高阶矩，因此也就忽略了量子涨落，对于高激发光场而言，这是一种合理的近似。其次，需要强调的是，演化过程仅由经典轨迹决定，这与准经典近似的核心思想高度一致。

为了阐明方程 (2.7) 所蕴含的物理意义，我们对每个模式采用"作用-角"变量(J,φ)[75]（action-angle variables）。在本文的研究背景下，这些变量可定义为：

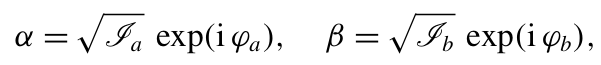(2.8)

因此，φ是相空间中的极角，而I与模式强度相关（见图 1）。

利用这些变量，方程 (2.7) 可以重写为简洁优美的形式：

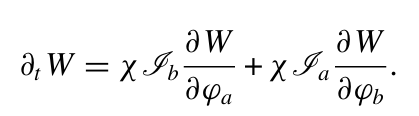(2.9)

由于∂/∂φ会产生相空间中的旋转，方程 (2.9) 表明，每个模式中的振幅会经历不同的旋转，其旋转角度与另一个模式的强度分量成正比 [76,77]。这一结果如图 1 所示：大致而言，阴影区域表示态在相空间中占据的区域。对于初始相干态，该区域为圆形；圆形的顶部对应较高的强度，因此比较底部产生更大的相移，最终形成椭圆型的噪声分布。
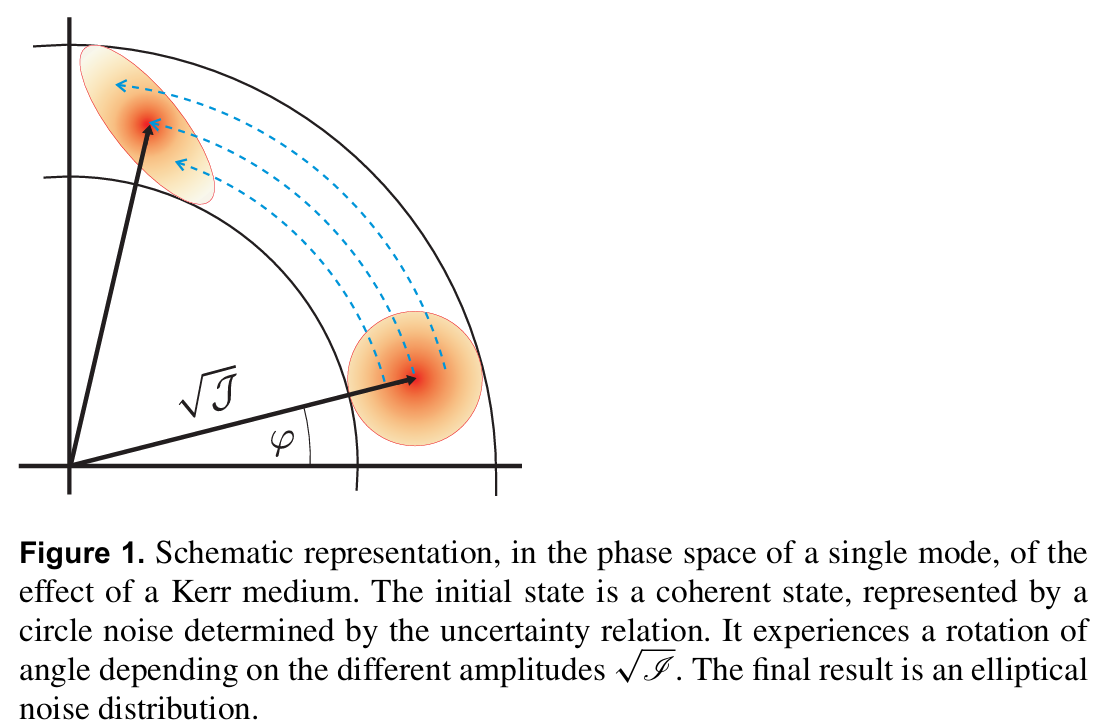初始态是相干态，由符合不确定关系的圆形噪声分布表示。它会发生一个角度旋转，旋转角度由不同的振幅决定。最终结果是一个椭圆形的噪声分布。

方程 (2.9) 可以很容易地求解：

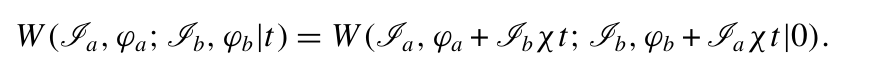(2.10)

如果我们再次假设初始态为双模相干态∣α0​,β0​⟩（其中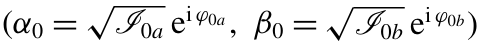），那么利用 (A.5)，方程 (2.10) 可简化为：

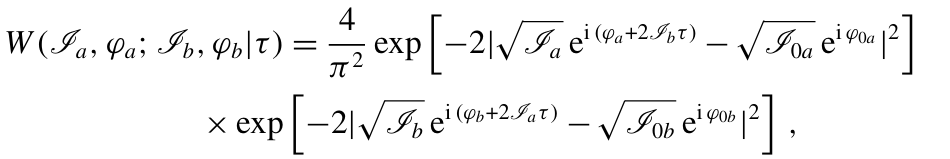（2.11）

其中我们引入了无量纲变量τ=χt/2。可以观察到，在τ=0时，维格纳函数由两个独立的高斯函数组成，而随着时间的推移，诱导产生的模式关联会导致形成非高斯态。

3. 模式关联动力学

双模高斯态是连续变量两体系统的最简单示例，也是量子信息领域的核心研究对象。因此，这些态的理论方面已得到了广泛深入的研究，并且已有多种定量表征方法可供使用 [78-82]。

这些高斯态的一个独特特征是，（除了局部位移之外）它们完全由协方差矩阵γ确定 ，其元素为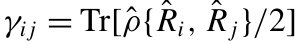，其中{ , }表示反对易子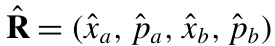，是相空间算子向量。该协方差矩阵可以表示为：

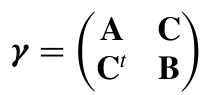(3.1)

其中，A和B分别是与模式a和b的约化态相关的协方差矩阵，而C则描述了这些模式之间的关联。γ的辛特征值为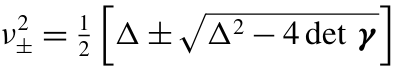：（3.2）

其中Δ=detA+detB+2detC。这些辛特征值包含了所有关键信息，并为表达基本特性提供了强大而简洁的方式。例如，一个高斯态是纠缠的，当且仅当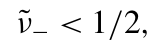：(3.3)其中，部分转置态的协方差矩阵的最小辛特征值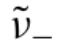是通过将detC替换为−detC（即对第二个系统进行时间反转，从而使其正则动量翻转）从​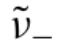得到的。

在图 2 中，我们绘制了态 (2.11) 的辛特征值​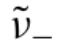的时间演化曲线，该曲线呈现出快速增长的趋势（在插图中，我们观察到一种波动行为，这种波动在更大的尺度上会变得平滑）。这种方法的主要局限性在于，如前所述，我们所研究的态会迅速变为非高斯态，因此判据 (3.3) 仅给出了一个充分条件。因此，我们只能在插图所示的短时间窗口内验证纠缠的存在。实际上，这一结论适用于所有现有的判据 [71,72]：如果一个态是纠缠的，某一特定的测试可能能够检测到其纠缠，也可能无法检测到；反之，如果某一特定测试未检测到纠缠，我们也不能得出该态是可分离的结论。
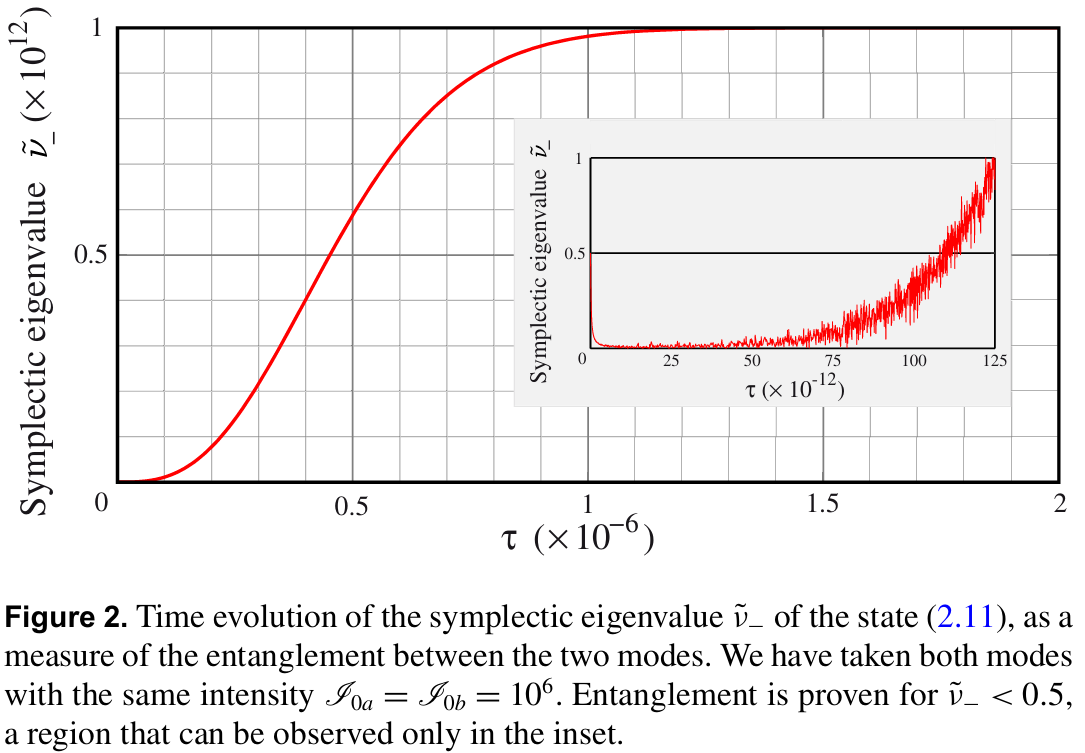图 2
态 (2.11) 的辛特征值ν~−的时间演化，该特征值用于衡量两个模式之间的纠缠程度。我们设定两个模式具有相同的强度I0a=I0b=106。当ν~−<0.5时，可证明存在纠缠，这一区域仅能在插图中观察到。

真正的非高斯纠缠只能通过涉及高阶矩的测量来揭示。在这方面，Shchukin 和 Vogel [83]（另见 [84,85]）提出了一套适用于任意态纠缠的必要和充分条件的通用层级结构。然而，将这种技术应用于我们的问题却非常困难，因为它需要验证非平凡的不等式，而这只能通过数值方法来实现。此外，该方法还涉及到确定具有极强振荡性和噪声特性的矩 [86]。

鉴于这些困难，我们转而评估两个模式的约化态的纯度。纯度与线性熵相关，并且与模间关联密切相关 [87]。这些局域纯度为：Pa​(τ)=Tra​[ρ^​a2​(τ)],Pb​(τ)=Trb​[ρ^​b2​(τ)](3.4)其中ρ^​a​(τ)=Trb​[ρ^​(τ)]和ρ^​b​(τ)=Tra​[ρ^​(τ)]分别是模式a和b的约化密度矩阵。如果我们采用双模维格纳函数 (2.11)，则纯度（例如Pa​(τ)）可以表示为：Pa​(τ)=8π​∫−ππ​dφa​∫0∞​dIa​[∫−ππ​dφb​∫0∞​dIb​W(Ia​,φa​;Ib​,φb​∣τ)]2(3.5)

对于两体系统，在纯态情况下，(3.4) 中的两个纯度相等 [88,89]。一般而言，对于混合态，这些量是不同的。在我们的研究中，经过冗长但直接的计算（为了完整性，附录 B 中概述了相关计算过程），Pa​(τ)可以表示为：Pa​(τ)=exp(−4I0b​−2I0a​)∑n=−∞∞​1+τ2n2In​(2I0a​)​exp(1+τ2n24I0b​​)=Pb​(τ)(3.6)其中In​(z)是第一类修正贝塞尔函数，最后的等式已通过数值实验仔细验证。这种令人惊讶的对称性可以归因于模式在克尔哈密顿量 (2.2) 中的参与方式。因此，我们在纯度的表示中省略了模式下标。

由于我们处理的是高激发光场（I0a​≫1），我们可以利用渐近展开式 [90]：In​(z)∼2πz​exp(z)​exp(−n2/(2z)),∣z∣≫1(3.7)

此外，由于τ≪1且 (3.6) 中的函数没有振荡，我们可以将求和替换为积分，最终结果为：P(τ)=4πI0a​​1​∫−∞∞​dx1+τ2x21​exp(−1+τ2x24I0b​τ2x2​−4I0a​x2​)

在图 3 中，我们以与图 2 相同的尺度绘制了该P(τ)的时间演化曲线。在τ=0时，约化纯度为 1，这与初始态由两个不相关的高斯函数组成的事实相符。随着时间的演化，纯度平稳下降（与辛特征值ν~−​的下降方式非常相似），这表明存在模式关联。以下对 (3.8) 的渐近估计支持了这一结论：P(τ)≃1+16I0a​I0b​τ2​1​(3.9)该式在I0b​τ≲1时成立。显然，这种形式的P(τ)在模式置换下是不变的。最后，P(τ)会趋向于其稳态值。

人们可能会好奇，到目前为止被忽略的量子涨落会如何改变这种准经典图像。对于我们此处处理的初始相干态这一特定情况，我们可以通过解析方法计算精确量子解的纯度。实际上，从 (2.5) 中我们可以很容易地推导出纯度的精确表达式：Pexact​(τ)=exp(−2I0a​−2I0b​)∑m,n=−∞∞​Im​(2I0a​)In​(2I0b​)exp(2imnτ)(3.12)

利用贝塞尔函数的性质，我们可以将其重新表示，这明确体现了上述对称性。实际上，考虑到 (3.7)，Pexact​(τ)表现为二维雅可比西塔函数 [90]，该函数具有周期性。然而，在我们所考虑的时间尺度上，这种周期性并不明显，我们可以再次将求和替换为积分，从而精确得到方程 (3.9)。

在图 3 的插图中，我们绘制了精确解 (3.12) 与准经典解 (3.8) 之间的差值。可以看出，在实际应用中，这两种解是一致的。这意味着前面所研究的关联具有量子性质，但高阶关联在此处并未发挥重要作用。

图 3 在与图 2 相同的条件下，纯度P(τ)的演化曲线，该纯度用于衡量两个模式之间的关联程度。

4. 偏振压缩

由于偏振模式a和b具有相同的频率且相互正交，它们的叠加会产生一般的椭圆偏振光。这意味着只需要三个独立的物理量即可描述：每个模式的振幅以及它们之间的相对相位。为了在量子层面上描述这一现象，采用斯托克斯算子 [91] 是非常有利的：S^x​=a^†b^+b^†a^,S^y​=i(a^b^†−a^†b^),S^z​=a^†a^−b^†b^再加上总光子数算子N^=a^†a^+b^†b^。根据 (2.1)，算子 (4.1) 满足角动量的对易关系：[S^k​,S^ℓ​]=2iεkℓm​S^m​,[N^,S^k​]=0(4.2)其中拉丁字母下标取值为{x,y,z}，εkℓm​是列维 - 奇维塔完全反对称张量。这种非对易性使得无法同时精确测量它们所表示的物理量，并直接导致了海森堡不等式 [92-95]：Δ2S^k​Δ2S^ℓ​≥εkℓm​∣⟨S^m​⟩∣2(4.3)其中Δ2A^=⟨A^2⟩−⟨A^⟩2表示方差。对于这一不确定关系，总能找到最大共轭算子对。这相当于建立一个基，在该基中，只有一个算子 (4.1) 具有非零的期望值，例如⟨S^k​⟩=⟨S^ℓ​⟩=0且⟨S^m​⟩=0。此时，唯一非平凡的海森堡不等式为：Δ2S^k​Δ2S^ℓ​≥∣⟨S^m​⟩∣2(4.4)

因此，偏振压缩可以合理地定义为以下条件 [96-100]：Δ2S^k​<∣⟨S^m​⟩∣<Δ2S^ℓ​(4.5)

需要注意的是，根据 (4.5) 定义的压缩态通常并非最小不确定态。

共轭算子对{S^k​,S^ℓ​}的选择绝不是唯一的：存在无穷多组算子{S^⊥​(ϑ),S^⊥​(ϑ+π/2)}，它们垂直于经典激发⟨S^m​⟩，并且对于所有的ϑ，都有⟨S^⊥​(ϑ)⟩=0。所有这些算子对都存在于Sk​−Sℓ​平面中，该平面被称为暗平面。一般的S^⊥​(ϑ)可以表示为：S^⊥​(ϑ)=S^k​cosϑ+S^ℓ​sinϑ(4.6)其中ϑ是相对于S^k​定义的角度。此时，条件 (4.5) 等价于：Δ2S^⊥​(ϑsq​)<∣⟨N^⟩∣<Δ2S^⊥​(ϑsq​+π/2)(4.7)其中S^⊥​(ϑsq​)是最大压缩算子，而S^⊥​(ϑsq​+π/2)是反压缩算子。

在许多实验中，两个模式具有相同的振幅，但相位差为π/2：⟨a^⟩=i⟨b^⟩。这种光为圆偏振光，满足⟨S^x​⟩=⟨S^z​⟩=0，⟨S^y​⟩=0，因此 (4.7) 可直接应用。

可以利用维格纳分布方法来评估这些定义中所涉及变量的时间演化：⟨S^⊥​(ϑ,τ)⟩=π2Re[eiϑ∫d2αd2βWS^⊥​(ϑ)​(α,β)W(α,β∣τ)]其中WS^⊥​(ϑ)​(α,β)是对应于算子S^⊥​(ϑ)的相空间函数（通常称为其符号）。从 (4.1) 和 (4.6) 可以清楚地看出，S^⊥​(ϑ)的符号可以直接根据基本模式振幅a^和b^的符号构建，

根据附录 A，我们知道这些符号分别为Wa^​(α)=α/π和Wb^​(β)=β/π。因此，我们得到：⟨S^y​(τ)⟩=(1+τ2)2I0​​exp(−1+τ22I0​τ2​),⟨S^x​(τ)⟩=⟨S^z​(τ)⟩=0其中I0​=Tr[ρ^​(0)N^]是态的初始平均光子数。二阶矩的计算方式类似，最终结果为：Δ2S^⊥​(ϑ,τ)​=I0​[1+(I0​/2)sin2ϑ]−sin2(ϑ/2)(1+4τ2)32I02​​exp(−1+4τ28I0​τ2​)−sin(2ϑ)(1+τ2)32I0​τ​(1+1+τ2I0​​)exp(−1+τ22I0​τ2​)​

这种形式体系的一个主要优点是，我们可以明确偏振压缩的时间演化规律。特别是对于足够短的时间τ≪1，我们可以将方程 (4.9) 和 (4.10) 展开到二阶，得到：⟨S^y​(τ)⟩≃I0​(1−I0​τ2),Δ2S^⊥​(ϑ,τ)≃I0​[1+4I02​sin2(ϑ)τ2]−2I02​sin(2ϑ)τ(4.11)因此，最优压缩角大致为：ϑsq​≃21​arccot(I0​τ)(4.12)即它起始于ϑsq​=π/4，并随着τ的增大缓慢趋向于 0。

5. 动力学在球面上的映射

可以将上一节中讨论的斯托克斯算子的作用转化为非常简单的相空间图像。为此，我们引入参数化表示 [101]：α=I​exp(iφa​)cos(θ/2),β=I​exp(iφa​)exp(−iϕ)sin(θ/2)其中φa​现在作为全局相位出现，相关的相对相位为ϕ=φa​−φb​。径向变量：I=Ia​+Ib​(5.2)表示总强度。参数θ和ϕ可以分别解释为庞加莱球面上的极角和方位角：θ描述了每个模式所携带的相对强度，而ϕ是模式之间的相对相位。利用这些新变量，方程 (2.9) 变为：∂t​W=χIb​∂φa​∂W​+χ(Ib​−Ia​)∂ϕ∂W​(5.3)

在 (5.1) 中，φa​作为无关的全局相位，我们可以对其进行积分而不会丢失相关信息，结果为：∂t​W(I,θ,ϕ)=−χIcosθ∂ϕ∂W(I,θ,ϕ)​(5.4)其用无量纲变量τ表示的解为：W(I,θ,ϕ∣τ)=W(I,θ,ϕ−2τIcosθ∣0)(5.5)

三个量(I,θ,ϕ)是庞加莱空间中的球坐标：Sx​=Isinθcosϕ,Sy​=Isinθsinϕ,Sz​=Icosθ(5.6)

利用笛卡尔坐标表示，方程 (5.5) 可以紧凑地表示为：W(Sx​,Sy​,Sz​∣τ)=π8​exp(−2I−2I0​)I0​(2σ(θ,ϕ,τ)​)其中：σ(θ,ϕ,τ)=2[II0​+Sz​S0z​+cos(2Sz​τ)(Sx​S0x​+Sy​S0y​)+sin(2Sz​τ)(Sy​S0x​−Sx​S0y​)](5.8)

对于前面提到的圆偏振光情况（S0x​=S0z​=0，S0y​=I0​），上式简化为：σ(θ,ϕ,τ)=2I0​[I+Sy​cos(2Sz​τ)−Sx​sin(2Sz​τ)]

在x−p正交相空间中，表示态的常用方法是通过不确定区域，该区域恰好是该态的维格纳函数W(x,p)的等值线。类似地，在每个固定的时间点，方程W(Sx​,Sy​,Sz​∣τ)=常数定义了在(Sx​,Sy​,Sz​)轴组成的庞加莱空间中的等值面，该等值面提供了关于态涨落的完整信息。在本文的补充材料中（可从stacks.iop.org/NJP/15/043038/mmedia获取），我们提供了一个动画，描绘了 (5.9) 中特定情况下维格纳函数 (5.7) 的时间演化。可以看出，态沿着最大压缩方向伸长。在图 4 中，我们展示了该动画在不同时间点的三个快照。

6. 耗散效应

当光在克尔介质中传播时，两种基本偏振模式之间的相对相位会发生退相干。处理这种退相干的一种合理方法是利用退相干的概念，我们大致将其理解为当系统与其环境相互作用时，出现不可逆且不可控的量子关联 [102]。

通常，退相干会伴随着耗散，即与环境之间的净能量交换。然而，考虑到克尔非线性的特性，我们关注的是纯退相干（也称为相移退相干）情况，在这种情况下，能量耗散过程可以忽略不计。目前已有一些模型 [103-107]，其中光子数保持不变，而相干性则显著衰减。然而，令人惊讶的是，这些模型尚未应用于保相 - 数的克尔动力学中。因此，我们通过主方程来模拟这种相移退相干：∂t​ρ^​=−i[H^,ρ^​]+γa​La^​[ρ^​]+γb​Lb^​[ρ^​](6.1)其中La^​[ρ^​]是林德布拉德超算子：La^​[ρ^​]=2a^†a^ρ^​a^†a^−(a^†a^)2ρ^​−ρ^​(a^†a^)2(6.2)γa​是相移退相干常数。模式b的表达式类似。此时，维格纳函数的方程 (2.9) 修改为：∂t​W=χIb​∂φa​∂W​+χIa​∂φb​∂W​+4γa​​∂φa2​∂2W​+4γb​​∂φb2​∂2W​(6.3)

再次利用变量 (5.6) 并对无关的整体相位φa​进行积分，该方程变为：∂t​W(I,θ,ϕ)=−χIcosθ∂ϕ∂W(I,θ,ϕ)​+4γ​∂ϕ2∂2W(I,θ,ϕ)​其中γ=γa​+γb​。其通解可以表示为：W(I,θ,ϕ∣t)=2π1​∫dϕ′Θ(ϕ−ϕ′−χtIcosθ∣tγ/4)W(I,θ,ϕ′∣0)(6.5)其中Θ(ϕ∣t)=∑k​exp(ikϕ−tk2)。在I0​≫1的极限下，这一精确结果简化为：W(I,θ,ϕ∣t)=π2II0​sinθsinθ0​​2exp(−2I−2I0​+4II0​​)​Θ(ϕ−ϕ0​−χtIcosθ∣4γt​+2II0​​sinθsinθ0​cos[(θ−θ0​)/2]​)

该维格纳函数演化的快照再次显示在图 4 中，其中γ=2γa​=2γb​=0.5χ。虽然在初始阶段，与无耗散情况相比，差异非常微小，但随着时间的推移，这种差异会变得越来越明显。

图 4 在时间τ=1.5×10−7、3.0×10−7和4.5×10−7（从左到右）时，维格纳函数W(Sx​,Sy​,Sz​∣τ)在水平10−4（相对于最大值）处的等值面（W=常数）。上图为无移相退相干情况，下图为移相退相干系数γ=0.5χ的情况。正交轴为Sx​、Sy​和Sz​，方框中心位于Sx​=Sz​=0、Sy​=106，轴刻度以τ=0时的（球面）等值线为单位，对应散粒噪声极限。

耗散演化过程中维格纳函数等值线的收缩意味着，由于相移退相干，态在相空间中变得 "弥散"。需要注意的是，椭球的形状和方向并未改变，仅其尺寸发生了变化，这表明偏振度有所降低。

我们还可以研究相移退相干对压缩的影响。为此，我们需要像方程 (4.9) 和 (4.10) 那样计算相应的物理量。最终得到：⟨S^y​(t)⟩=(1+τ2)2I0​​exp(−1+τ22I0​τ2​−4γt​)(6.7)Δ2S^⊥​(ϑ,t)​=I0​[1+(I0​/2)sin2ϑ]−sin2(ϑ/2)(1+4τ2)3I02​​exp(−1+4τ28I0​τ2​−γt)−sin(2ϑ)(1+τ2)32I0​τ​(1+1+τ2I0​​)exp(−1+τ22I0​τ2​−4γt​)​

对于短时间τ≪1，可以证明最优压缩角近似为：ϑsq​≃21​arccot(I0​τ+4χγ​)

需要注意的是，与方程 (4.12) 不同，在存在相移退相干的情况下，对于给定的时间τ，最优压缩角更接近 0。在某种意义上，相移退相干使得等值面椭球旋转得更快（同时也使其尺寸变小）。最后，最优压缩量为：Δ2S^⊥opt​(ϑ,t)−∣⟨S^y​(t)⟩∣≃2I02​τ[I0​τ+4χγ​−1+(I0​τ+4χγ​)2​](6.10)

在图 5 中，我们绘制了不同γ/χ比值下的最优压缩量。可以清楚地观察到，随着γ/χ的增大，该量逐渐减小。

图 5 最优压缩量Δ2S^ϑopt​(t)−∣⟨S^y​(t)⟩∣。图中γ/χ的值分别为 0（黑色实线）、0.2（绿色虚线）、1（红色点线）、5（蓝色点划线）和 20（橙色虚线）。

7. 结论

总之，我们提出了一种准经典近似方法来描述光在交叉克尔介质中的传播过程。即使所考虑的态是强场且忽略了量子关联，我们仍然观测到了纠缠和压缩等非经典效应。有趣的是，在准经典极限下，一旦产生关联，它们就会在系统中保持下去，这与精确演化中观察到的周期性退相干现象不同。我们还构建了这些介质中相移退相干过程的模型，结果表明，耗散会显著影响偏振度，但对其矢量方向的影响则相对较小。

致谢

本文得到了欧盟第七框架计划（Q-ESSENCE 项目资助）、西班牙科学与创新部（资助编号 FIS2008-04356 和 FIS2011-26786）、马德里康普顿斯大学 - BSCH 项目（资助编号 GR-920992）以及墨西哥国家科学技术委员会（资助编号 106525）的资金支持。

附录 A. 双模维格纳函数

本附录简要回顾了与本文研究问题相关的维格纳分布。对于单模a，由密度矩阵ρ^​描述的态的维格纳函数定义为：W(α)=Tr[ρ^​a​w^(α)](A.1)其中核w^(α)为：w^(α)=π21​∫dλexp(αλ∗−α∗λ)D^(α)(A.2)因此，它是位移算子D^(α)的傅里叶变换，其中：D^(α)=exp(αa^†−α∗a^)(A.3)

需要注意的是，标准相干态∣α⟩是通过位移算子D^(α)作用于真空态产生的，即：∣α⟩=D^(α)∣0⟩(A.4)

对于相干态∣α0​⟩，其维格纳函数为：W(α)=π2​exp(−2∣α−α0​∣2)(A.5)

在更一般的情况下，维格纳函数可以解释为密度矩阵ρ^​的相空间符号。这一概念可以推广到任意算子O^，使其符号为：WO^​(α)=Tr[O^w^(α)](A.6)

特别是对于基本模式算子a^，我们有：Wa^​=πα​(A.7)

利用W(α)，我们可以通过以下规则将任意算子演化映射为微分方程 [105]：a^ρ^​ρ^​a^​↦(α+21​∂α∗∂​)W(α),a^†ρ^​↦(α∗−21​∂α∂​)W(α),↦(α−21​∂α∗∂​)W(α),ρ^​a^†↦(α∗+21​∂α∂​)W(α)​经过分解 (2.6) 后，上式变为：δa^ρ^​ρ^​δa^​↦21​∂α∗∂​W,δa^†ρ^​↦−21​∂α∂​W,↦−21​∂α∗∂​W,ρ^​δa^†↦21​∂α∂​W​(A.9)模式b的表达式类似。

双模维格纳函数是方程 (A.1) 的直接推广，即：W(α,β)=Tr[ρ^​w^(α)w^(β)](A.10)

本文所需的其他性质可以直接推广到这种双模情况。

附录 B. 约化密度矩阵的纯度

为了完整性，此处给出了获得约化纯度Pa​(τ)的表达式 (3.6) 的一些中间步骤，其定义为：Pa​(τ)=8π​∫−ππ​dφa​∫0∞​dIa​[∫−ππ​dφb​∫0∞​dIb​W(Ia​,φa​;Ib​,φb​∣τ)]2(B.1)

利用维格纳函数 (2.11) 的显式形式，我们有：Pa​(τ)=π32​​∫−ππ​dφa​dφ1​dφ2​∫0∞​dIa​dI1​dI2​exp(−4Ia​−4I0a​−2I1​−2I2​−4I0b​)×exp[2Ia​I0a​​(exp(iφa​+2iI1​τ)+exp(iφa​+2iI2​τ)+exp(−iφa​−2iI1​τ)+exp(−iφa​−2iI2​τ))]×exp(4I1​I0b​​cosφ1​+4I2​I0b​​cosφ2​)​

在第二行中，我们可以将指数函数按exp(iφa​)和exp(−iφa​)的幂级数展开，将其余变量视为固定系数。然后，可以显式地对φa​进行积分，结果为：2π∑k=0∞​(k!)2(4Ia​)k(2I0a​)k​{1+cos[2(I1​−I2​)τ]}k(B.3)

结合项exp(−4Ia​)，可以立即对Ia​进行积分，得到：4π​exp{2I0a​[1+cos(2(I1​−I2​)τ)]}(B.4)该式替换了方程 (B.2) 中的第二行。对φj​的积分将 (B.2) 的最后一行转化为：(2π)2I0​(4I1​I0b​​)I0​(4I2​I0b​​)(B.5)

最后，为了对I1​和I2​进行积分，我们将贝塞尔函数展开为幂级数，即：I0​(4Ij​I0b​​)=∑k=0∞​(k!)2(2Ij​)k(2I0b​)k​(B.6)以及 (B.4) 中的指数函数：exp[2I0a​cos(2(I1​−I2​)τ)]=∑n=−∞∞​In​(2I0a​)exp[2i(I1​−I2​)τ](B.7)

所有这些都使得可以直接对I1​和I2​进行积分，得到：P(τ)=4exp(−4I0b​−2I0a​)∫0∞​dI1​dI2​exp(−2I1​−2I2​)×k,m=0∑∞​(k!)2(m!)2(2I1​)k(2I2​)m(2I0b​)k+m​n=−∞∑∞​In​(2I0a​)exp(2i(I1​−I2​)τ)​

从这个表达式中，可以直接得到纯度的结果 (3.6)。

参考文献

1. Braginsky V B 1968 Sov. Phys.-JETP 26 831--4
2. Unruh W G 1979 Phys. Rev. D 19 2888--96
3. Milburn G J and Walls D F 1983 Phys. Rev. A 28 2065--70
4. Imoto N, Haus H A and Yamamoto Y 1985 Phys. Rev. A 32 2287--92
5. Alsing P, Milburn G J and Walls D F 1988 Phys. Rev. A 37 2970--8
6. Grangier P, Levenson J A and Poizat J P 1998 Nature 396 537--42
7. Sanders B C and Milburn G J 1989 Phys. Rev. A 39 694--702
8. König F, Büchler B, Rechtenwald T, Leuchs G and Sizmann A 2002 Phys. Rev. A 66 043810
9. Xiao Y F, Özdemir S K, Gaddam V, Dong C H, Imoto N and Yang L 2008 Opt. Express 16 21462--75
10. Milburn G J and Holmes C A 1986 Phys. Rev. Lett. 56 2237--40
11. Yurke B and Stoler D 1986 Phys. Rev. Lett. 57 13--6
12. Tombesi P and Mecozzi A 1987 J. Opt. Soc. Am. B 4 1700--9
13. Gantsog T and Tanás R 1991 J. Mod. Opt. 38 1537--58
14. Wilson-Gordon A D, Bužek V and Knight P L 1991 Phys. Rev. A 44 7647--56
15. Tara K, Agarwal G S and Chaturvedi S 1993 Phys. Rev. A 47 5024--9
16. Luis A, Sánchez-Soto L L and Tanás R 1995 Phys. Rev. A 51 1634--43
17. Szabo S, Adam P, Janszky J and Domokos P 1996 Phys. Rev. A 53 2698--710
18. Chumakov S M, Frank A and Wolf K B 1999 Phys. Rev. A 60 1817--23
19. Korolkova N, Loudon R, Gardavsky G, Hamilton M W and Leuchs G 2001 J. Mod. Opt. 48 1339--55
20. Vitali D, Fortunato M and Tombesi P 2000 Phys. Rev. Lett. 85 445--8
21. Jian Z, Ming Y, Yan L and Zhuo-Liang C 2009 Chin. Phys. Lett. 26 100301
22. Zhu M, Yin X and Yuan G 2011 Opt. Commun. 284 3483--7
23. Turchette Q A, Hood C J, Lange W, Mabuchi H and Kimble H J 1995 Phys. Rev. Lett. 75 4710--3
24. Semião F L and Vidiella-Barranco A 2005 Phys. Rev. A 72 064305
25. Matsuda N, Mitsumori Y, Kosaka H, Edamatsu K and Shimizu R 2007 Appl. Phys. Lett. 91 171119
26. Azuma H 2008 J. Phys. D: Appl. Phys. 41 025102
27. You H and Franson J 2012 Quantum Inf. Process. 11 1627--51
28. Xia Y, Song J, Lu P M and Song H S 2011 J. Phys. B: At. Mol. Opt. Phys. 44 025503
29. Kok P, Lee H and Dowling J P 2002 Phys. Rev. A 66 063814
30. Munro W J, Nemoto K, Beausoleil R G and Spiller T P 2005 Phys. Rev. A 71 033819
31. Greentree A D, Beausoleil R G, Hollenberg L C L, Munro W J, Nemoto K, Prawer S and Spiller T P 2009 New J. Phys. 11 093005
32. Schmidt H and Imamoğlu A 1996 Opt. Lett. 21 1936--8
33. Imamoğlu A, Schmidt H, Woods G and Deutsch M 1997 Phys. Rev. Lett. 79 1467--70
34. Werner M J and Imamoğlu A 1999 Phys. Rev. A 61 011801
35. Dey T N and Agarwal G S 2007 Phys. Rev. A 76 015802
36. Hau L, Harris S, Dutton Z and Behroozi C 1999 Nature 397 594--8
37. Kang H and Zhu Y 2003 Phys. Rev. Lett. 91 093601
38. Castellanos-Beltran M A and Lehnert K W 2007 Appl. Phys. Lett. 91 083509
39. Mallet F, Ong F R, Palacios-Laloy A, Nguyen F, Bertet P, Vion D and Esteve D 2009 Nature Phys. 5 791--5
40. Bergeal N, Schackert F, Metcalfe M, Vijay R, Manucharyan V E, Frunzio L, Prober D E, Schoelkopf R J, Girvin S M and Devoret M H 2010 Nature 465 64--8
41. Bermel P, Rodriguez A, Joannopoulos J D and Soljačić M 2007 Phys. Rev. Lett. 99 053601
42. Mohapatra A K, Bason M G, Butscher B, Weatherill K J and Adams C S 2008 Nature Phys. 4 890--4
43. Brandão F G S L, Hartmann M J and Plenio M B 2008 New J. Phys. 10 043010
44. Babourina-Brooks E, Doherty A and Milburn G J 2008 New J. Phys. 10 105020
45. Ritze H H and Bandilla A 1979 Opt. Commun. 29 126--30
46. Heiman D, Hellwarth R W, Levenson M D and Martin G 1976 Phys. Rev. Lett. 36 189--92
47. Yuen H P and Shapiro J H 1979 Opt. Lett. 4 334--6
48. Levenson M D, Shelby R M and Perlmutter S H 1985 Opt. Lett. 10 514--6
49. Levenson M D, Shelby R M, Aspect A, Reid M and Walls D F 1985 Phys. Rev. A 32 1550--62
50. Kitagawa M and Yamamoto Y 1986 Phys. Rev. A 34 3974--88
51. Joneckis L G and Shapiro J H 1993 J. Opt. Soc. Am. B 10 1102--20
52. Sundar K 1996 Phys. Rev. A 53 1096--111
53. Schmitt S, Ficker J, Wolff M, König F, Sizmann A and Leuchs G 1998 Phys. Rev. Lett. 81 2446--9
54. Boyd R W 1999 J. Mod. Opt. 46 367--78
55. Shelby R M, Levenson M D and Bayer P W 1985 Phys. Rev. B 31 5244--52
56. Elser D, Andersen U L, Korn A, Glöckl O, Lorenz S, Marquardt C and Leuchs G 2006 Phys. Rev. Lett. 97 133901
57. Agrawal G P 2007 Nonlinear Fiber Optics 4th edn (New York: Academic)
58. Lee H W 1995 Phys. Rep. 259 147--211
59. Schroek F E 1996 Quantum Mechanics on Phase Space (Dordrecht: Kluwer)
60. Schleich W P 2001 Quantum Optics in Phase Space (Berlin: Wiley-VCH)
61. Heller E J 1976 J. Chem. Phys. 65 1289--98
62. Lee H W and Scully M O 1980 J. Chem. Phys. 73 2238--42
63. Balzer B, Dilthey S, Stock G and Thos M 2003 J. Chem. Phys. 119 5795--804
64. Hillery M, O'Connell R F, Scully M O and Wigner E P 1984 Phys. Rep. 106 121--67
65. Drobný G, Bandilla A and Jex I 1997 Phys. Rev. A 55 78--93
66. Banaszek K and Knight P L 1997 Phys. Rev. A 55 2368--75
67. Bandilla A, Drobný G and Jex I 2000 J. Opt. B: Quantum Semiclass. Opt. 2 265--70
68. Stobińska M, Milburn G J and Wódkiewicz K 2008 Phys. Rev. A 78 013810
69. Corney J F, Heersink J, Dong R, Josse V, Drummond P D, Leuchs G and Andersen U L 2008 Phys. Rev. A 78 023831
70. Sizmann A and Leuchs G 1999 The optical Kerr effect and quantum optics in fibers Progress in Optics vol 39 ed E Wolf (Amsterdam: Elsevier) pp 373--469
71. Duan L M, Giedke G, Cirac J I and Zoller P 2000 Phys. Rev. Lett. 84 2722--5
72. Simon R 2000 Phys. Rev. Lett. 84 2726--9
73. Weiss U 1999 Quantum Dissipative Systems (Singapore: World Scientific)
74. Scully M O and Zubairy M S 2001 Quantum Optics (Cambridge: Cambridge University Press)
75. Goldstein H 1980 Classical Mechanics (New York: Addison-Wesley)
76. Heersink J, Gaber T, Lorenz S, Glöckl O, Korolkova N and Leuchs G 2003 Phys. Rev. A 68 013815
77. Heersink J, Josse V, Leuchs G and Andersen U L 2005 Opt. Lett. 30 1192--4
78. Braunstein S L and van Loock P 2005 Rev. Mod. Phys. 77 513--77
79. Ferraro A, Olivares S and Paris M G A 2005 Gaussian States in Quantum Information (Naples: Bibliopolis)
80. Wanga X B, Hiroshima T, Tomita A and Hayashi M 2007 Phys. Rep. 448 1--111
81. Adesso G and Illuminati F 2007 J. Phys. A: Math. Theor. 40 7821--80
82. Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H and Lloyd S 2012 Rev. Mod. Phys. 84 621--69
83. Shchukin E and Vogel W 2005 Phys. Rev. Lett. 95 230502
84. Agarwal G S and Biswas A 2005 New J. Phys. 7 211
85. Hillery M and Zubairy M S 2006 Phys. Rev. Lett. 96 050503
86. Gomes R M, Salles A, Toscano F, Souto Ribeiro P H and Walborn S P 2009 Proc. Natl Acad. Sci. USA 106 21517--20
87. Mazzola L, Bellomo B, Lo Franco R and Compagno G 2010 Phys. Rev. A 81 052116
88. De Pasquale A, Facchi P, Parisi G, Pascazio S and Scardicchio A 2010 Phys. Rev. A 81 052324
89. Pasquale A D, Facchi P, Giovannetti V, Parisi G, Pascazio S and Scardicchio A 2012 J. Phys. A: Math. Theor. 45 015308
90. Abramowitz M and Stegun I A (ed) 1984 Handbook of Mathematical Functions (New York: Dover)
91. Luis A and Sánchez-Soto L L 2000 Quantum phase difference, phase measurements and Stokes operators Progress in Optics vol 41 ed E Wolf (Amsterdam: Elsevier) pp 421--81
92. Sehat A, Söderholm J, Björk G, Espinoza P, Klimov A B and Sánchez-Soto L L 2005 Phys. Rev. A 71 033818
93. Marquardt C, Heersink J, Dong R, Chekhova M V, Klimov A B, Sánchez-Soto L L, Andersen U L and Leuchs G 2007 Phys. Rev. Lett. 99 220401
94. Björk G, Söderholm J, Sánchez-Soto L L, Klimov A B, Ghiu I, Marian P and Marian T A 2010 Opt. Commun. 283 4440--7
95. Müller C R, Stoklasa B, Peuntinger C, Gabriel C, Řeháček J, Hradil Z, Klimov A B, Leuchs G, Marquardt C and Sánchez-Soto L L 2012 New J. Phys. 14 085002
96. Chirkin A S, Orlov A A and Parashchuk D Y 1993 Quantum Electron. 23 870--4
97. Korolkova N, Leuchs G, Loudon R, Ralph T C and Silberhorn C 2002 Phys. Rev. A 65 052306
98. Luis A and Korolkova N 2006 Phys. Rev. A 74 043817
99. Mahler D, Joanis P, Vilim R and de Guise H 2010 New J. Phys. 12 033037
100. Ma J, Wang X, Sun C P and Nori F 2011 Phys. Rep. 509 89--165
101. Klimov A B, Delgado J and Sánchez-Soto L L 2006 Opt. Commun. 258 210--8
102. Zurek W H 2003 Rev. Mod. Phys. 75 715--75
103. Shao J, Ge M L and Cheng H 1996 Phys. Rev. E 53 1243--5
104. Mozyrsky D and Privman V 1998 J. Stat. Phys. 91 787--99
105. Gardiner C W and Zoller P 2004 Quantum Noise 2nd edn (Berlin: Springer)
106. Breuer H P and Petruccione F 2002 The Theory of Open Quantum Systems (Oxford: Oxford University Press)
107. Klimov A B, Romero J L, Sánchez-Soto L L, Messina A and Napoli A 2008 Phys. Rev. A 77 033853

文章pdf