前缀和算法
对于一个数组,我们求数组中某个区间的和,如果通过遍历相加的话,时间复杂度为n。若分别求m个区间的和,则所需时间复杂度为m*n。因此我们可以使用前缀和算法优化它的时间复杂度。

我们可以利用一个数组,存储上面数组中0到每个位置区间的和。
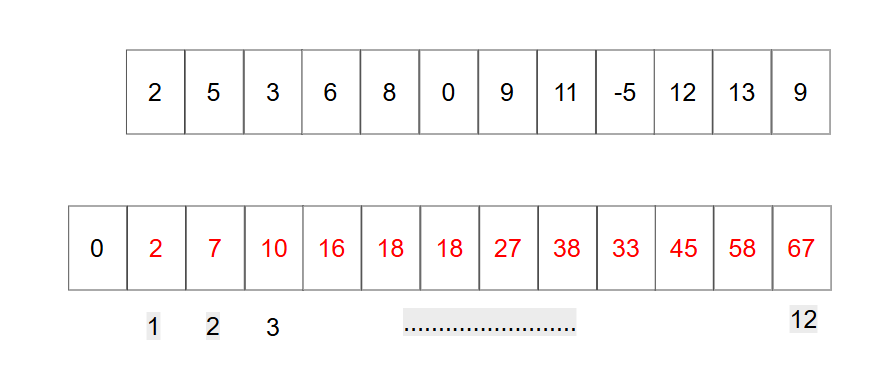
如上图,下面的前缀和数组存储,上面区间和时是从数组1位置开始的,而不是数组0位置开始的。1位置存储的就是上面数组第一个数字到第一个数字区间的和,第2个位置存放的是上面数组第一个数字到第二个数组区间的和。这里前缀和数字从1开始存放,而不是从0开始存放,是为了后面处理边界的问题。
这里我们求前缀和数组中的值时,可以使用前缀和数组该位置对应的上面数组的值加上,前缀和数组该位置上一个位置里面的值,从而优化计算。如,求前缀和数组6下标的值,可以用上面数组第6个数加上前缀和下标5的值。
现在我们知道了从第1个数,到第n个数区间的和,那么我们要求如4到8之间的和,该怎么求呢?
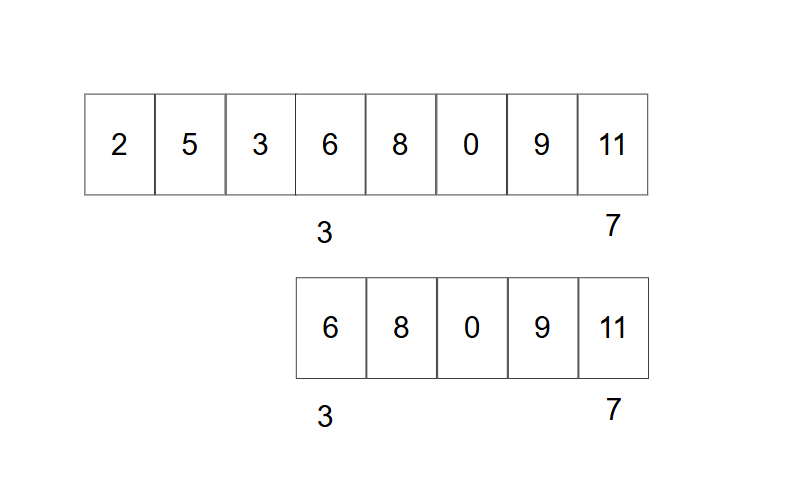
第4个数和第8个数,在上面数组对应坐标为3和7,我们发现,该区间的和,就等于第1个数到第8个数的和减去第一个数的到第3个数的和。
因此转化为公式就是:
如求第n个数,到第m个数这个区间的和。
前缀和数组[m] - 前缀和数组[n-1]。
这里我们可以看出,为什么前缀和数组要从下标1开始存,比如求第1个数到第4个数区间和,带入公式为前缀和数组[4] - 前缀和数组[0]。