【音视频开发】镜头畸变矫正 (LDC) 技术指南

镜头畸变矫正 (LDC) 技术指南

文章目录

镜头畸变矫正 (LDC) 技术指南
- 1. 技术原理
- - 1.1 镜头畸变的主要类型
  - - 1.1.1 桶形畸变 (Barrel Distortion)
    - 1.1.2 枕形畸变 (Pincushion Distortion)
    - 1.1.3 须状畸变 (Mustache Distortion)
  - 1.2 数学建模
  - - 1.2.1 Brown-Conrady 模型 (普通镜头)
    - 1.2.2 Kannala-Brandt 模型 (鱼眼镜头)
- 1. 实现方法
- - 2.1 标定流程详解
  - 2.2 核心代码实现
  - 2.3 获取相机内参和畸变系数
- 1. 矫正效果展示
- 1. 常见问题与注意事项
- 1. 总结

1. 技术原理

镜头畸变（Lens Distortion）是光学成像系统中常见的几何失真现象，主要由透镜表面的曲率和光线通过透镜时的折射不均匀引起。在计算机视觉和摄影测量中，准确的畸变模型是实现高精度测量和图像还原的基础。

1.1 镜头畸变的主要类型

镜头畸变主要分为径向畸变（Radial Distortion）和切向畸变（Tangential Distortion）。其中径向畸变最为常见，表现为图像点沿着径向方向发生偏移。

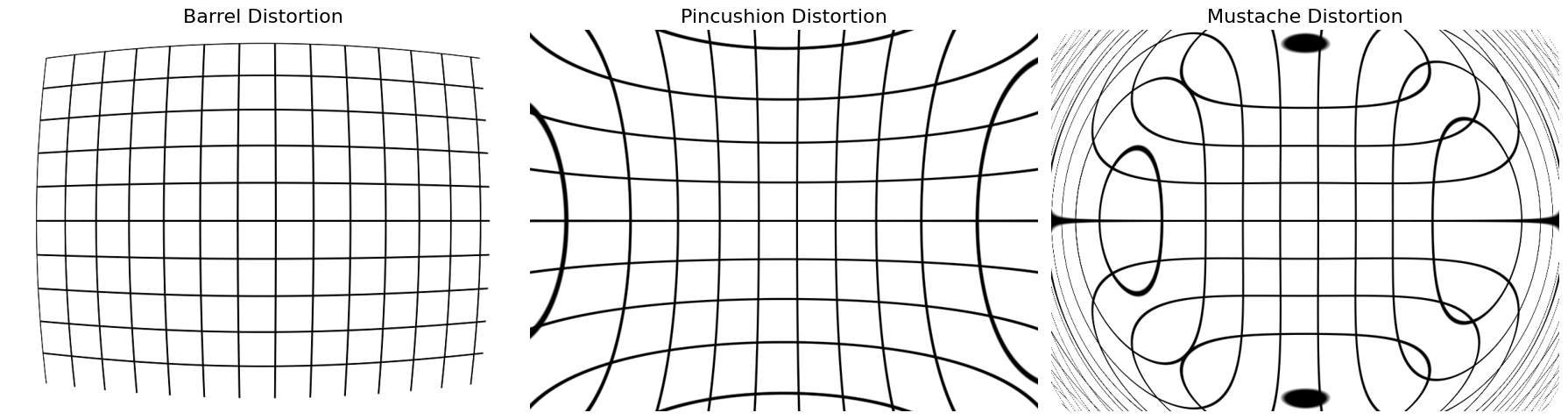
1.1.1 桶形畸变 (Barrel Distortion)

特征：图像放大率随着与光轴距离的增加而减小。
表现：正方形物体成像后呈现出边线向外弯曲的"桶状"。
成因：常见于广角镜头，视场角越大，畸变越明显。
数学描述 ：畸变系数 k1<0k_1 < 0k1<0。

1.1.2 枕形畸变 (Pincushion Distortion)

特征：图像放大率随着与光轴距离的增加而增加。
表现：正方形物体成像后呈现出边线向内凹陷的"枕状"。
成因：常见于长焦镜头。
数学描述 ：畸变系数 k1>0k_1 > 0k1>0。

1.1.3 须状畸变 (Mustache Distortion)

特征：桶形畸变和枕形畸变的混合体。
表现：图像中心表现为桶形畸变，而边缘表现为枕形畸变（或反之），线条呈现波浪状。
成因：复杂的光学透镜组设计中可能出现。

1.2 数学建模

在计算机视觉库（如 OpenCV）中，通常使用 Brown-Conrady 模型 来描述普通镜头的畸变，而对于超广角或鱼眼镜头，则使用 Kannala-Brandt 模型。

1.2.1 Brown-Conrady 模型 (普通镜头)

该模型结合了径向畸变和切向畸变。

假设未畸变的理想归一化图像坐标为 (x,y)(x, y)(x,y)，距离光轴中心的半径 r=x2+y2r = \sqrt{x^2 + y^2}r=x2+y2 。

径向畸变公式：
xdistorted=x(1+k1r2+k2r4+k3r6) x_{distorted} = x (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) xdistorted=x(1+k1r2+k2r4+k3r6)
ydistorted=y(1+k1r2+k2r4+k3r6) y_{distorted} = y (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) ydistorted=y(1+k1r2+k2r4+k3r6)

切向畸变公式：

（由透镜与成像平面不平行引起）
xtangential=x+[2p1xy+p2(r2+2x2)] x_{tangential} = x + [2p_1xy + p_2(r^2 + 2x^2)] xtangential=x+[2p1xy+p2(r2+2x2)]
ytangential=y+[p1(r2+2y2)+2p2xy] y_{tangential} = y + [p_1(r^2 + 2y^2) + 2p_2xy] ytangential=y+[p1(r2+2y2)+2p2xy]

综合畸变模型：

最终的畸变坐标 (x′,y′)(x', y')(x′,y′) 为两者之和。

k1,k2,k3k_1, k_2, k_3k1,k2,k3 ：径向畸变系数。k1k_1k1 起主导作用，正负决定了畸变方向（桶形或枕形）。
p1,p2p_1, p_2p1,p2：切向畸变系数。通常数值很小，但在高精度装配误差分析中不可忽略。

1.2.2 Kannala-Brandt 模型 (鱼眼镜头)

对于鱼眼镜头，传统的 Brown 模型不再适用，因为它假设 rrr 较小时成立，而鱼眼镜头的入射角 θ\thetaθ 很大。Kannala-Brandt 模型基于入射角 θ\thetaθ 进行建模。

假设入射角为 θ\thetaθ，畸变后的径向距离 rdr_drd 为：
rd(θ)=k1θ+k2θ3+k3θ5+k4θ7 r_d(\theta) = k_1 \theta + k_2 \theta^3 + k_3 \theta^5 + k_4 \theta^7 rd(θ)=k1θ+k2θ3+k3θ5+k4θ7

OpenCV 的 cv2.fisheye 模块即采用了此模型。

2. 实现方法

基于 OpenCV 的畸变矫正流程通常包含三个步骤：标定数据采集 、相机内参计算 、图像矫正。

2.1 标定流程详解

准备标定板：通常使用棋盘格（Chessboard），因为角点特征明显，易于检测。
多角度拍摄：采集 15-20 张不同角度、距离、方位的标定板图片。
提取角点 ：使用 cv2.findChessboardCorners 自动查找内角点。
相机标定 ：使用 cv2.calibrateCamera 计算内参矩阵和畸变系数。

2.2 核心代码实现

以下是一个完整的 Python 示例，演示如何从标定到矫正的全过程。

python 复制代码

import numpy as np
import cv2
import glob

def calibrate_and_undistort(image_folder, pattern_size=(9, 6), square_size=1.0):
    """
    相机标定与畸变矫正函数
    :param image_folder: 标定图片文件夹路径
    :param pattern_size: 棋盘格内角点数目 (columns, rows)
    :param square_size: 棋盘格方块的物理尺寸 (例如 20mm)
    """
    # 1. 准备物体坐标 (0,0,0), (1,0,0), (2,0,0) ....,(8,5,0)
    objp = np.zeros((pattern_size[0] * pattern_size[1], 3), np.float32)
    objp[:, :2] = np.mgrid[0:pattern_size[0], 0:pattern_size[1]].T.reshape(-1, 2)
    objp = objp * square_size

    # 存储所有图像的物体点和图像点
    objpoints = [] # 3D points in real world space
    imgpoints = [] # 2D points in image plane

    images = glob.glob(f'{image_folder}/*.jpg')
    
    if not images:
        print("未找到标定图片，请检查路径。")
        return

    img_shape = None

    # 2. 检测角点
    for fname in images:
        img = cv2.imread(fname)
        gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        img_shape = gray.shape[::-1]

        # 寻找棋盘格角点
        ret, corners = cv2.findChessboardCorners(gray, pattern_size, None)

        if ret:
            objpoints.append(objp)
            # 亚像素级角点优化
            corners2 = cv2.cornerSubPix(gray, corners, (11,11), (-1,-1), 
                                        (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001))
            imgpoints.append(corners2)
            
            # 可视化（可选）
            # cv2.drawChessboardCorners(img, pattern_size, corners2, ret)
            # cv2.imshow('img', img)
            # cv2.waitKey(100)

    cv2.destroyAllWindows()

    # 3. 相机标定
    # ret: 重投影误差
    # mtx: 相机内参矩阵
    # dist: 畸变系数 (k1, k2, p1, p2, k3)
    ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, img_shape, None, None)

    print(f"标定完成！重投影误差: {ret:.4f}")
    print("相机内参矩阵:\n", mtx)
    print("畸变系数:\n", dist)

    # 4. 畸变矫正测试
    img = cv2.imread(images[0])
    h, w = img.shape[:2]
    
    # 优化新的相机内参矩阵（保留更多图像信息）
    newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))

    # 方法一：使用 undistort
    dst = cv2.undistort(img, mtx, dist, None, newcameramtx)

    # 裁剪掉黑色边框（可选）
    x, y, w, h = roi
    dst = dst[y:y+h, x:x+w]
    
    cv2.imwrite('calibresult.png', dst)
    print("矫正图像已保存为 calibresult.png")
    
    return mtx, dist

# 使用示例 (假设当前目录下有 calibration_images 文件夹)
# mtx, dist = calibrate_and_undistort('./calibration_images')

2.3 获取相机内参和畸变系数

通过上述 cv2.calibrateCamera 函数，我们可以得到两个核心结果：

相机矩阵 (mtx) ：
A=[fx0cx0fycy001] A = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} A=⎣⎡fx000fy0cxcy1⎦⎤

其中 fx,fyf_x, f_yfx,fy 为焦距（像素单位），cx,cyc_x, c_ycx,cy 为主点坐标（光心在图像上的投影）。
畸变系数 (dist) ：

返回一个 1x5 的向量 (k1, k2, p1, p2, k3)。
- 如果使用的是 fisheye 模块，返回的是 1x4 的向量 (k1, k2, k3, k4)。

3. 矫正效果展示

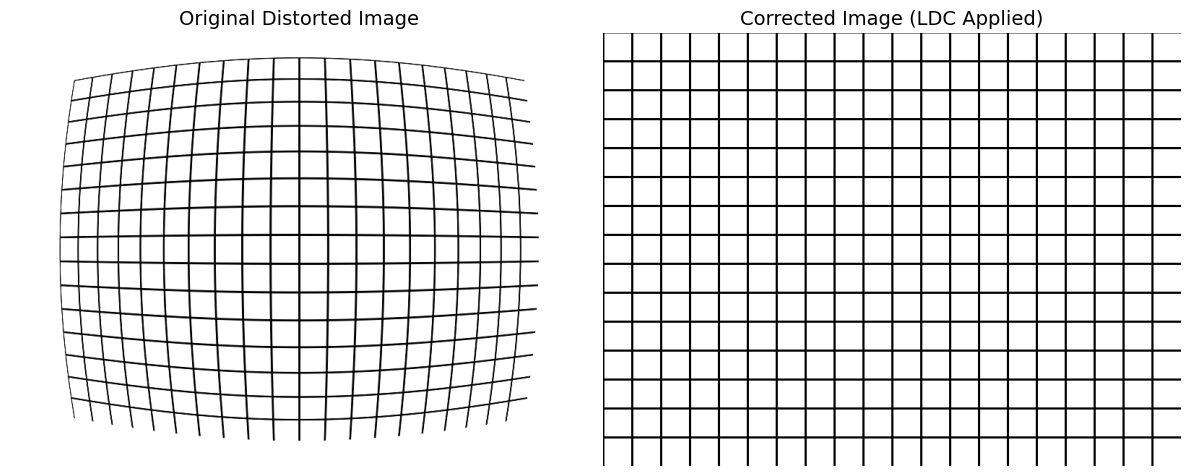
下图展示了强畸变图像经过标定参数矫正后的效果。可以看到，原本弯曲的网格线被拉直，恢复了真实的几何结构。

4. 常见问题与注意事项

标定板质量：标定板必须保持平整，打印精度直接影响标定结果。建议将打印纸粘贴在硬纸板或亚克力板上。
光照条件：拍摄时避免反光和过暗，保证角点清晰可见。
角点覆盖：拍摄时应让标定板覆盖画面的各个角落（边缘、中心、远近），以准确计算全图的畸变参数。
鱼眼矫正 ：对于视场角超过 160 度的鱼眼镜头，务必使用 cv2.fisheye 模块，普通模型无法收敛。

5. 总结

镜头畸变矫正（LDC）是机器视觉系统中的重要预处理步骤。通过理解畸变产生的物理原理（径向与切向），利用数学模型（Brown-Conrady 或 Kannala-Brandt）进行参数化描述，并借助 OpenCV 强大的标定工具，我们可以高效地消除图像失真，为后续的目标检测、SLAM 或 3D 重建提供准确的几何输入。