视频讲解:Mujoco 蒙特卡洛采样统计机械臂可达工作空间(非Matlab)_哔哩哔哩_bilibili
代码仓库:https://github.com/LitchiCheng/mujoco-learning
前面总是提到机械臂的可达空间,那怎么计算,有什么公式吗?
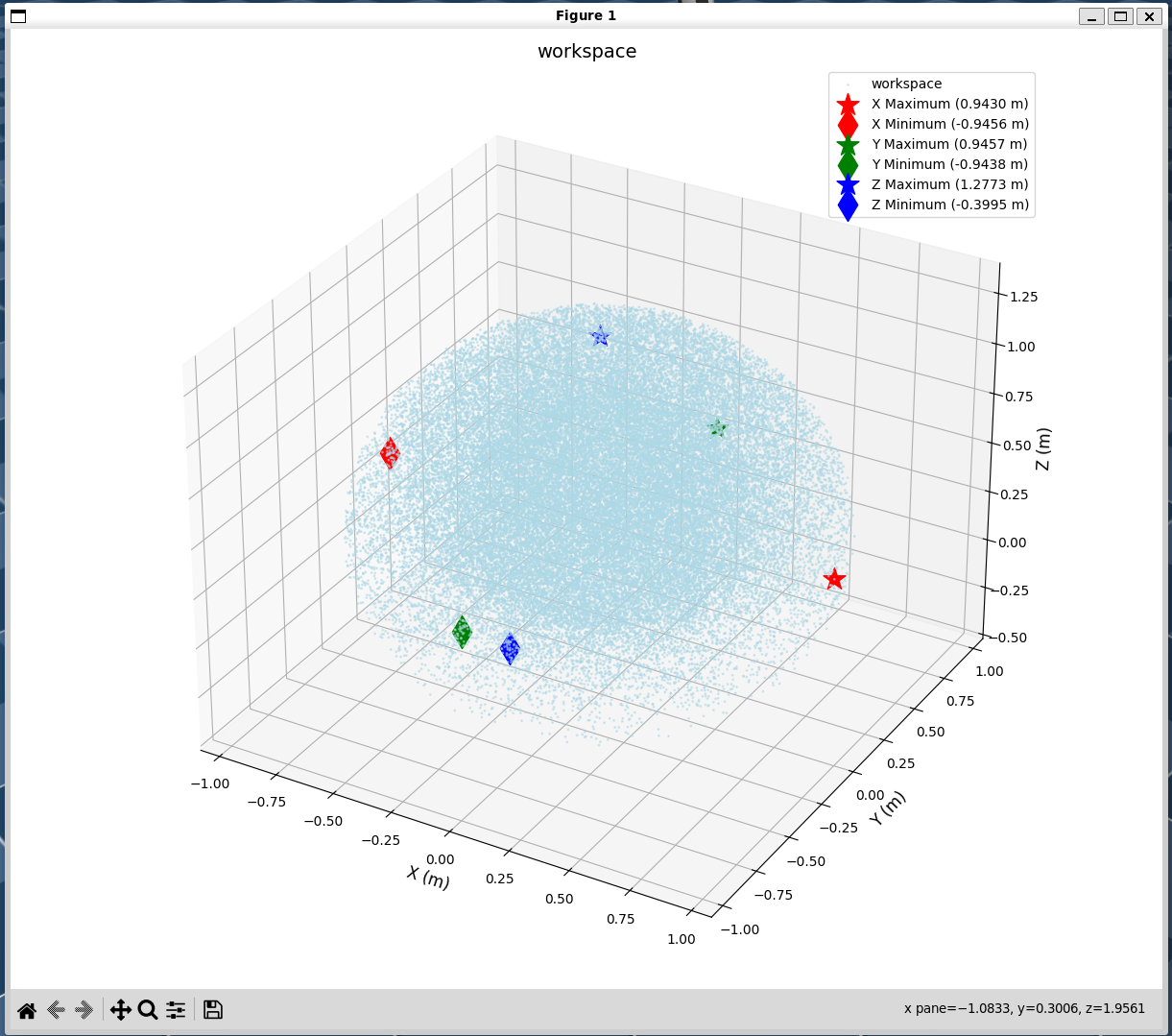
使用蒙特卡洛采样,通过大样本概率统计替代精确推导,生成随机分布的关节空间(限制关节范围),再进行正运动学 fk 即可求得机械臂末端的可达空间
self.ee_body_name = "ee_center_body"
self.kine = kdl_ik.Kinematics(self.ee_body_name)
self.kine.buildFromURDF(self.urdf_path, "link0")
workspace = []
for _ in range(self.sample_num):
q = PyKDL.JntArray(self.model.nq)
for i in range(self.model.nq):
q[i] = np.random.uniform(self.model.jnt_range[i][0], self.model.jnt_range[i][1])
# fk
mat = self.kine.fk(q)
x, y, z, _, _, _ = utils.mat2transform(mat)
workspace.append([x, y, z])最后将x,y,z的集合通过散点图画出来,同时打印下分别的最大最小值,但这个值通常也不是无脑使用,除非只关心某一个维度,不然还是要一起考虑,一般控制前可以通过ik是否可以得到解来判断是否最终控制是有效的。
完整代码如下:
import src.kdl_kinematic as kdl_kinematic
import PyKDL
import numpy as np
import os
import mujoco_viewer
import mujoco
import utils
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class GetWorkspace(mujoco_viewer.CustomViewer):
def __init__(self, scene_path, urdf_path, sample_num = int(10e4)):
super().__init__(scene_path, 3, azimuth=-45, elevation=-30)
self.path = scene_path
self.urdf_path = urdf_path
self.sample_num = sample_num
def runBefore(self):
self.ee_body_name = "ee_center_body"
self.kine = kdl_kinematic.Kinematics(self.ee_body_name)
self.kine.buildFromURDF(self.urdf_path, "link0")
workspace = []
for _ in range(self.sample_num):
q = PyKDL.JntArray(self.model.nq)
for i in range(self.model.nq):
q[i] = np.random.uniform(self.model.jnt_range[i][0], self.model.jnt_range[i][1])
# fk
mat = self.kine.fk(q)
x, y, z, _, _, _ = utils.mat2transform(mat)
workspace.append([x, y, z])
self.plotWorkspace(np.array(workspace))
def plotWorkspace(self, workspace):
# X轴
x_max = workspace[:, 0].max()
x_min = workspace[:, 0].min()
x_max_idx = np.argmax(workspace[:, 0])
x_min_idx = np.argmin(workspace[:, 0])
x_max_point = workspace[x_max_idx]
x_min_point = workspace[x_min_idx]
# Y轴
y_max = workspace[:, 1].max()
y_min = workspace[:, 1].min()
y_max_idx = np.argmax(workspace[:, 1])
y_min_idx = np.argmin(workspace[:, 1])
y_max_point = workspace[y_max_idx]
y_min_point = workspace[y_min_idx]
# Z轴
z_max = workspace[:, 2].max()
z_min = workspace[:, 2].min()
z_max_idx = np.argmax(workspace[:, 2])
z_min_idx = np.argmin(workspace[:, 2])
z_max_point = workspace[z_max_idx]
z_min_point = workspace[z_min_idx]
print(f"X轴:最大值 {x_max:.4f} m | 最小值 {x_min:.4f} m")
print(f"Y轴:最大值 {y_max:.4f} m | 最小值 {y_min:.4f} m")
print(f"Z轴:最大值 {z_max:.4f} m | 最小值 {z_min:.4f} m")
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(workspace[:,0], workspace[:,1], workspace[:,2], s=1, alpha=0.5, c='lightblue', label='workspace')
ax.scatter(x_max_point[0], x_max_point[1], x_max_point[2],
s=300, c='red', marker='*', label=f'X Maximum ({x_max:.4f} m)')
ax.scatter(x_min_point[0], x_min_point[1], x_min_point[2],
s=300, c='red', marker='d', label=f'X Minimum ({x_min:.4f} m)')
ax.scatter(y_max_point[0], y_max_point[1], y_max_point[2],
s=300, c='green', marker='*', label=f'Y Maximum ({y_max:.4f} m)')
ax.scatter(y_min_point[0], y_min_point[1], y_min_point[2],
s=300, c='green', marker='d', label=f'Y Minimum ({y_min:.4f} m)')
ax.scatter(z_max_point[0], z_max_point[1], z_max_point[2],
s=300, c='blue', marker='*', label=f'Z Maximum ({z_max:.4f} m)')
ax.scatter(z_min_point[0], z_min_point[1], z_min_point[2],
s=300, c='blue', marker='d', label=f'Z Minimum ({z_min:.4f} m)')
ax.set_xlabel('X (m)', fontsize=12)
ax.set_ylabel('Y (m)', fontsize=12)
ax.set_zlabel('Z (m)', fontsize=12)
ax.set_title('workspace', fontsize=14)
ax.legend(fontsize=10)
# plt.tight_layout()
# plt.show()
def runFunc(self):
plt.tight_layout()
plt.show(block=False)
plt.pause(0.001)
if __name__ == "__main__":
urdf_file = "model/franka_panda_urdf/robots/panda_arm.urdf"
SCENE_XML_PATH = 'model/franka_emika_panda/scene_pos.xml'
robot = GetWorkspace(SCENE_XML_PATH, urdf_file, sample_num=int(5e4))
robot.run_loop()