目录
[1 最优传输基础](#1 最优传输基础)
[2 Grover算法](#2 Grover算法)
[2.1 定义与问题描述](#2.1 定义与问题描述)
[2.2 算法步骤](#2.2 算法步骤)
[2.3 代码示例](#2.3 代码示例)
[3 总结](#3 总结)
摘要
本周首先学习了最优传输的核心思想与部分应用,了解了蒙日问题与康托洛维奇松弛的思想与数学表示;其次学习了Grover算法,了解了其定义、算法步骤与几何表示,还利用代码进行了实现;同时还拓展了无结构搜索问题、Oracle黑盒与单位算子等概念。
Abstract
This week, I first studied the core ideas and some applications of optimal transport, learning about the concepts and mathematical formulations of the Monge problem and Kantorovich relaxation. Secondly, I studied Grover's algorithm, understanding its definition, algorithmic steps, and geometric representation, and also implemented it in code. Additionally, I explored concepts such as the unstructured search problem, the Oracle black box, and unitary operators.
1 最优传输基础
最优传输研究的是如何用最小的成本,把一堆东西从一个地方搬到另一个地方,并变成指定的新形状。它总是涉及两个分布,一个初始,一个目标,它的强大之处在于能知道两个分布有多不同,以及如何以最小的代价从初始分布变为目标分布,而传统的方法无法做到,比如单纯比较均值会完全忽略分布形状。
为了直观理解最优传输,蒙日在1781年提出了沙堆问题,即:
假设有两堆沙土,分别由两个区域(或分布)表示。我们想要将第一堆沙土(源分布)移动到第二堆沙土(目标分布)的位置,并且重新排列成目标分布的形状。每次移动沙土都需要成本,且成本与移动的距离还有沙土的质量有关,问题是如何以最小的总成本完成这个搬运和重塑任务。
这一比喻将抽象的分布转换问题可视化,从而揭示了最优传输的本质,即在质量守恒的约束下,最小化整体转换成本。它的数学表示为:
即寻找一个传输映射 T,能够将分布 转化为分布
,并且使得在这个过程中产生的总成本最小。
蒙日问题是第一个最优传输问题,提供了分布变换的基本范式,其局限性在于要求每个源点映射到唯一目标点(即T,确定性传输),不允许质量拆分,解可能不存在。
在1942年,列昂尼德·康托洛维奇(Leonid Kantorovich)提出了该问题的松弛形式。他通过引入一个耦合测度 ,不再要求质量必须由一个映射 T 运输,而是允许将一个源点的质量拆分并运送到多个目标点。耦合测度
是
上的联合概率分布,其边缘分布分别为
和
,故该问题的数学表示为:
康托洛维奇问题是线性规划问题(在离散情况下)或无限维线性规划问题(在连续情况下),因此更容易处理。而且它的解总是存在的,并且当存在一个最优的确定性映射时,可以退化为蒙日问题的解。
最优传输的经典应用包括但不限于如下几个:
在图像处理上,把一张彩色图片(分布A)的风格变成另一张油画(分布B)的风格,最优传输可以找到颜色之间的最佳匹配,在改变风格的同时,保持图片结构;
在自然语言领域,可以比较两篇文章的词频分布。传统方法只能看出"都有这些词",但最优传输能看出,第一篇文章的"快乐"一词在含义上更对应第二篇文章的"喜悦"一词;
在机器学习领域,比如让计算机生成人脸,可以把生成的人脸分布,向真实人脸分布进行"最优传输"来优化模型。又比如Wasserstein距离(推土机距离)就是基于最优传输理论定义的,它比传统指标(如KL散度)更平滑、更能反映分布形状的差异。
另外关于最优传输,在后续的学习中可能会有一些误区或者混淆,在此提前说明:
首先最优传输不是简单的最近邻匹配,而是全局优化,需要考虑所有点的协调,有时可能需要舍近求远以达到全局最优;
其次最优传输不是只适用于离散点集,还适用于连续分布(前面的康托洛维奇问题)、图像、文本等任何可以表示为质量分布的东西;
最后,虽然经典的最优传输问题的计算复杂度较高(如线性规划方法),存在不实用的问题,但现代算法如Sinkhorn算法(熵正则化)大大降低了计算复杂度,使其能够应用于大规模实际问题。因此,最优传输近年来得到了广泛应用。
2 Grover算法
2.1 定义与问题描述
Grover算法也被称为量子搜索算法,专门用于处理无结构的搜索问题。
p.s. 无结构搜索问题,即在一个没有任何辅助结构(如排序)的数据库中搜索一个特定的元素。
面对这类问题,由于没有结构可利用,任何未检查的元素都可能是目标元素,因此不管使用何种经典算法,平均情况下都需要检查一半的元素,而最坏情况下需要检查所有元素();但使用Grover算法则可实现平方加速(
)。
它要解决的问题可被描述为:给定一个包含 个元素的无序数据库与一个 Oracle 函数 f(x),当 x 为目标项时,函数值为1,否则为0。问题的目标就是使用最少的查询次数找到使函数值为1的 x 。
p.s. 在计算复杂性理论中,Oracle(预言机)是一个黑盒,它可以在一步计算中回答某个问题。在经典计算中,Oracle函数通常是一个不知道其内部结构,但可以询问其函数值的布尔函数;在量子计算中,Oracle是一个量子黑盒。
2.2 算法步骤
Grover算法由以下步骤组成:
首先,根据问题确定判断条件或布尔表达式(Oracle),确保它对合法组合返回 True,对不合法组合返回 False;
其次,创建并初始化 n 个量子比特,并逐个应用 Hadamard 变换(H门)以得到所有可能的均匀叠加态;
接着,通过 Oracle 筛选出符合条件的组合,并进行扩散变换,即计算此时的系数平均值,将其乘以2,再减去相应量子态前的系数得到对应的新系数(此时合法的量子态系数会增大,而不合法的会减小);
最后,对量子态进行测量,此时能够以较高的概率得到目标元素。
其中,第三步通过迭代来实现,每次迭代都会包括筛选与扩散变换两个操作。
筛选操作的基本作用是识别、标记目标态,并对其相位进行翻转,用酉算子 表示,其具体数学描述如下:
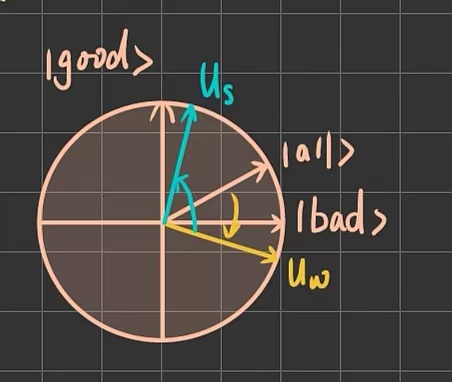
在几何上,可以想象一个二维平面,横轴代表所有非目标态的均匀叠加,纵轴代表目标态,该操作就是将状态向量关于横轴进行反射。它只是识别与标记,不改变幅度,同时采用的相位翻转能为后续的干涉创造条件。

扩散变换的基本作用则在于以所有态的振幅平均值为轴线进行反射,将高于平均的振幅变得更高,低于平均的变得更低,用酉算子 表示,其具体数学描述如下:
其中 是初始的均匀叠加态,I 是单位算子。
p.s. 单位算子(Identity Operator)在量子力学和量子计算中是一个基本概念。它是一个线性算子,作用在任何量子态上都保持该态不变。
扩散变换相当于关于 的反射,即在二维平面上,将状态向量关于
方向进行反射。
它可以通过以下步骤实现(扩散算子):
首先,将所有量子比特进行 Hadamard 变换;
其次,进行条件相位翻转,即将除全零态以外的所有态乘以-1,其算子为:,可以通过先对所有量子比特应用X门,再应用多控制Z门,最后再次应用X门实现;
最后,将所有量子比特进行 Hadamard 变换以恢复原基。
2.3 代码示例
Grover算法的代码示例如下:
python
from qiskit import QuantumCircuit, transpile
from qiskit.providers.basic_provider import BasicSimulator
from qiskit.visualization import plot_histogram
import math
def grover_search(n, oracle_circuit, iterations=None):
#n: 量子比特数
#oracle_circuit: 实现Oracle的量子电路
#iterations: 迭代次数,默认为最优值
N = 2 ** n
# 计算最优迭代次数
if iterations is None:
theta = math.asin(1 / math.sqrt(N))
iterations = int(round(math.pi / (4 * theta) - 0.5))
# 创建量子电路
qc = QuantumCircuit(n, n)
# 初始化:应用Hadamard变换
qc.h(range(n))
# Grover迭代
for _ in range(iterations):
# 应用Oracle
qc.compose(oracle_circuit, inplace=True)
# 应用扩散算子
qc.h(range(n))
qc.x(range(n))
qc.h(n - 1)
qc.mcx(list(range(n - 1)), n - 1) #当前n-1个比特均为1时,对索引为n-1的比特应用翻转
qc.h(n - 1) # 往上三步为多控制Z门的实现
qc.x(range(n))
qc.h(range(n))
# 测量
qc.measure(range(n), range(n))
return qc, iterations
# 示例:在4个元素中搜索|11⟩
n = 2
oracle = QuantumCircuit(n)
# 受控Z门,应用在量子比特0和1之间,只涉及两个量子比特
oracle.cz(0, 1)
# 执行Grover搜索
qc, iterations = grover_search(n, oracle)
print(f"最优迭代次数: {iterations}")
# 模拟
simulator = BasicSimulator()
compiled_circuit = transpile(qc, simulator)
job = simulator.run(compiled_circuit, shots=1024)
result = job.result()
counts = result.get_counts(compiled_circuit)
print("测量结果:", counts)
print("量子电路:")
print(qc)关于代码中的最优迭代次数:
初始均匀叠加态可被表示为:
其中, 为目标态,
为所有非目标态的均匀叠加,
,
。由此,当N很大时,
。
同时,假设经过k次迭代,那么状态会变为:
为了使目标态概率最大化,则希望 ,即
,进而可得:
这也就是最优的迭代次数。如果迭代次数超过该值,状态会旋转过头,目标态概率会下降。这也是Grover算法的特性,即概率随迭代次数呈周期性变化。
上述代码打印得到:
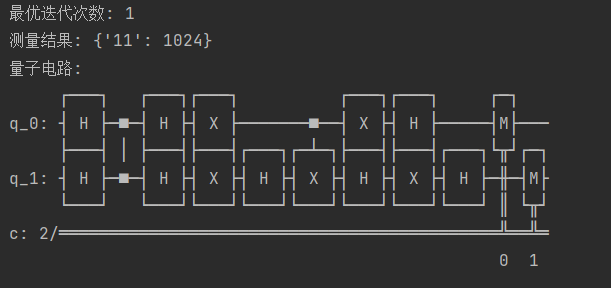
3 总结
本周首先学习了最优传输的基础知识,包括其核心思想及应用,其次学习了Grover算法,了解了其步骤并进行了代码实现。后续学习重心可能在论文的阅读复现、实际调参和画图,量子计算的学习会稍微放一放,只偶尔回顾,最优传输的部分本周初次接触感觉有理解难度,学习速度会比较慢。