目录
- 章节导读与精读
- 本章相关公式推导
- 中文参考译文
-
- Introduction
- [2.1 Class A Amplifiers and Linear Amplifiers](#2.1 Class A Amplifiers and Linear Amplifiers)
- [2.2 Gain Match and Power Match](#2.2 Gain Match and Power Match)
- [2.3 Introduction to Load-Pull Measurements](#2.3 Introduction to Load-Pull Measurements)
- [2.4 Loadline Theory](#2.4 Loadline Theory)
- [2.5 Package Effects and Refinements to Load-Pull Theory](#2.5 Package Effects and Refinements to Load-Pull Theory)
- [2.6 Drawing the Load-Pull Contours on CAD Programs](#2.6 Drawing the Load-Pull Contours on CAD Programs)
- [2.7 Class A Design Example](#2.7 Class A Design Example)
- [2.8 Conclusions](#2.8 Conclusions)
- 参考文献
章节导读与精读
本章主要围绕负载线匹配和负载牵引这一话题,介绍其必要性、理论分析模型与实际的修正,并通过一个实例讲解使用方法。
2.1小节指出了A类放大器与线性放大器的关系,仅在理想情况下A类放大器才是线性放大器,在实际中A类放大器包含一定的非线性分量,依靠了滤波才使得输出中基本只含有基波分量。
2.2小节通过一组测量得到的数据,从功率角度讲解了PA设计时相比共轭匹配,负载线匹配的优势。
2.3小节讲到了从2.2小节的数据可以看出负载与功率输出存在一定的函数关系 ,需要通过负载牵引测试获取,介绍了负载牵引测试的一些基础知识。
2.4小节延续2.3小节的话题,深入介绍负载牵引中的负载线理论,提出等功率轮廓非理想的圆形 ,并以理想的晶体管和电路模型演示如何绘制获取等功率轮廓 。最后指出分析是基于晶体管输出端端口为参考面。
2.5小节延续2.4小节最后提到的,负载线理论是基于晶体管输出端口来分析的,但实际封装中存在一些寄生参数,需要进行映射 ;并分析了寄生参数导致等功率轮廓发生偏转的合理性 。最后讲到了2.4小节的分析是基于理想情况,在实际使用中需要对一些参数进行修正。
2.6小节介绍了在CAD仿真软件中如何用简单的程序实现负载牵引,即使用串联电感与并联电容。
2.7小节使用一个A类放大器的设计实例 ,介绍通过负载牵引和负载线理论,如何将非线性的设计过程变为线性的设计过程。
本章相关公式推导
2.4小节-负载线理论公式推导,另起一篇文章
中文参考译文
Introduction
本章将展示如何将第 1 章中的一些概念进一步发展,形成一种简单但完整的线性射频功率放大器设计策略。基本上,一个线性功率放大器可以使用与小信号设计相同的基本匹配原理来设计,但其输出端采用的是功率匹配,这通常看起来并不是共轭匹配。
在某些方面,功率放大器的设计与低噪声放大器的设计具有相似性:为了获得器件最佳的噪声性能,其输入端必须呈现一个反射系数,而这个反射系数通常与输入阻抗的共轭匹配有显著偏离。在线性功率放大器的情况下,为了从器件中提取最大功率,必须在输出端对器件呈现一个功率匹配阻抗。
在过去,射频与微波频率下的功率匹配阻抗的准确值被认为只能通过实验测量获得。像噪声匹配数据一样,设计者要么亲自测量,要么(更理想地)由器件制造商提供。因此,"负载牵引"的科学与艺术便应运而生,并一直沿用至今,发展为昂贵但功能强大的计算机控制测量系统。
本章将介绍负载牵引技术及其在线性功率放大器设计中的应用。实际的负载牵引系统以及更高级的谐波负载牵引技术将在第 12 章中进一步讨论。本章的核心思想在于展示:对于下一节定义的 Class A 类型放大器,存在一个简单的理论框架,可以相当准确地预测实验生成的负载牵引数据。
2.1 Class A Amplifiers and Linear Amplifiers
通常人们认为"A 类"与"线性"这两个术语几乎是同义的,至少在 RF 功率放大器领域里是这样。然而事实上,A 类放大器往往并不线性,而高度线性的放大器也不一定,甚至很少采用 A 类结构。
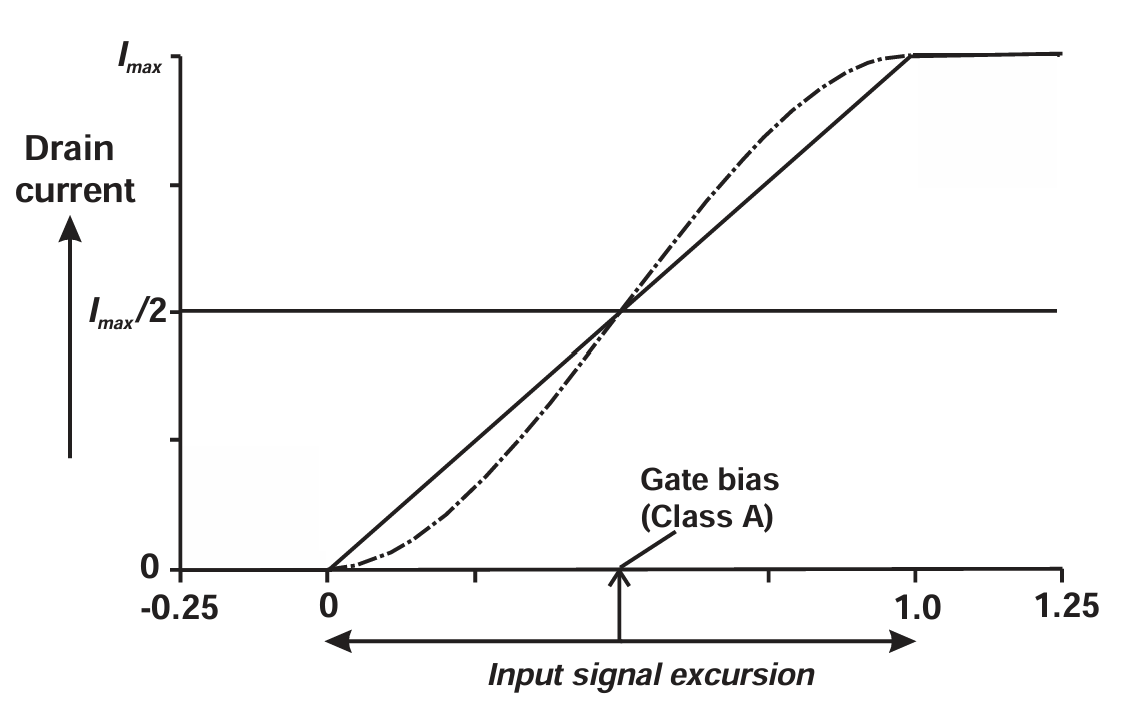
图2.1 FET Class A bias point (see also Figure 1.3). The solid line represents an ideal strongly nonlinear response, used for simplified analysis; the dotted line shows the more realistic weakly nonlinear response, with low-level harmonic generation even at low signal levels.
A 类放大器在传统定义上非常容易描述。图 2.1 回顾了第 1 章图 1.3 中的理想"强非线性"器件传输特性。这样的器件在截止与饱和之间被假设为完全线性的。如果将器件线性区域的正中央作为偏置点构建放大器,只要射频驱动信号不超过该线性区域的边界,就可以得到完全线性的工作。如果驱动信号是完美正弦波,则输出电流同样会是无谐波的正弦波。这就是最经典的 A 类放大器。
图 2.1 中的放大器在驱动信号不超过规定范围时显然也是线性的。因此,在这个理想情况下,A 类放大器在一定的输入范围内是线性的。然而在实际中,线性区域总会存在一些弱非线性,这一点在第 1.3 节讨论过,并在图 2.1 中有所体现。随着驱动电平增加,这些非线性会变得越来越明显。为了构建 A 类功率放大器,必须让器件在更大摆幅下工作,这会使其经过传输特性中越来越强的非线性区域,最终达到硬限幅的边界。在这种情况下,输出电流中将含有显著的谐波成分。通常,输出电流源会接一个有反应性的匹配网络,用于将 50Ω 环境变换成所需的负载阻抗。这些网络通常为低通结构,因此由跨导非线性产生的谐波会被大幅衰减。这让 A 类放大器具有一种看似"非常干净"的输出形象。但当输入改换为调制信号时,这种干净的形象就不再成立,往往可以看到明显的频谱扩展或互调失真。正如第 9 章将更详细讨论的,产生谐波的失真机制同样会对幅度调制信号造成频谱失真。总体而言,A 类放大器确实比第 3 章介绍的 A B 类放大器"干净";而 A B 类放大器为了更高效率,会主动利用器件特性中强非线性区域。
- A类的完全线性仅表现在理想情况中,因为此时晶体管的行为被描述为线性放大;但实际上晶体管存在弱非线性(在小信号时)或是强非线性(器件在更大摆幅下工作),因此A类放大器的输出中不可避免地含有谐波,因而不是线性放大器。
2.2 Gain Match and Power Match
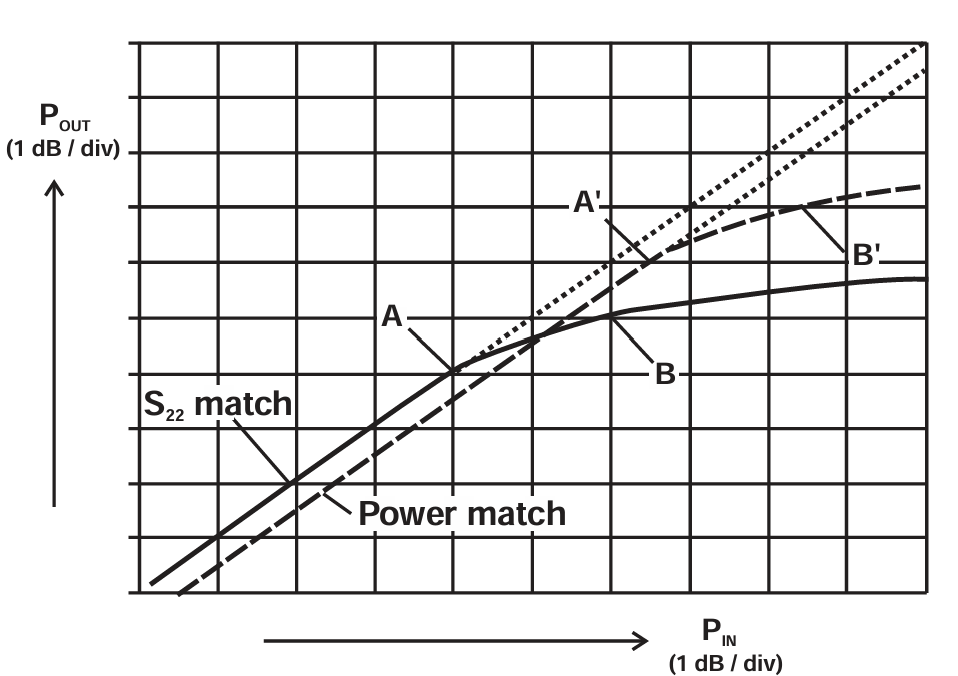
图2.2 Compression characteristics for conjugate (S22) match (solid curve) and power match (dashed curve). The 1 dB compression points (B, B') and maximum linear power points (A, A') show improvements under power-matched conditions.
图 2.2 展示了一个 A 类放大器在两种不同输出匹配条件下的功率传输特性。实线对应的是在较低驱动电平下实现共轭匹配时的响应。图中点 A 和 B 分别表示最大线性功率点和1 dB 压缩点。在 RF 放大器领域中,1 dB 压缩点 已经成为一个标准,用来描述放大器或晶体管的输出能力。它也是实际能够维持"线性"工作的一个限制点 。我们将在后面看到,1 dB 压缩点实际上代表的是一个中等非线性的位置,而不是弱非线性。因此,本章我们将主要关注点 A,也就是增益压缩开始出现的初始点。
- 1 dB 压缩点处输出功率比输入功率与增益之和小 1 dB,属于较明显的非线性,即中等非线性,不能通过简单的幂级数描述。但从其是线性增益 1 dB 的压缩点的角度,经常被用来描述器件的线性度。
在典型工作条件下,共轭匹配会导致可实现的 1 dB 压缩功率明显低于正确功率调谐的情况。图 2.2 中的虚线表示经过输出功率最佳化的调谐匹配。在 A 和 B 这两个点上,共轭匹配下的输出功率都比功率调谐后的情况低 2 dB。对于昂贵的功率晶体管来说,这 2 dB 的损失是不能忽视的,因为它会转换为更高的系统成本。因此,功率匹配必须被重视,即使在低信号电平(图 2.2 左下角)下,它的增益可能比共轭匹配少 1 dB 左右。图 2.2 的这两条曲线可以与第 1.5 图中的两条线进行比较,其本质原因相同,只是在 RF 世界里我们通常无法直接观测电流与电压,而只能依赖最终的 RF 输出功率。
需要注意的一点是无论我们以哪一种方式定义 RF 输出功率,功率匹配通常都能带来约 2 dB 的提升。也就是说,最大线性功率(A → A′)提升约 2 dB,1 dB 压缩功率(B → B′)提升约 2 dB。这是非常典型的现象,尽管只能算定性描述。不同器件和工艺技术之间,这个差值可能从 0.5 dB 到 3--4 dB 不等,但总的来说,功率匹配带来的功率提升,在不同增益压缩水平下相对是稳定的。
- 功率匹配在低输入时输出功率会低于共轭匹配,但是当输入升高、甚至达到或超过 1 dB增益压缩点时,功率匹配的输出功率一定会大于共轭匹配。这是定性的,具体高出多少取决于器件和工艺。
2.3 Introduction to Load-Pull Measurements
图 2.2 中的两条功率扫描曲线表明,输出功率与输出匹配之间存在某种函数关系。逻辑上的下一步,就是测量两个以上的数据点。这种测量被称为 负载牵引测量,这个名称可能源于对 RF 振荡器进行的类似测量。在最简单的形式中,负载牵引测试系统由被测器件和其输出端的一种带校准的可调谐网络构成。输入端通常也会是可调谐的,但主要目的是为了提高器件的功率增益,因此输入匹配一般会在每个频率点都被固定为接近良好匹配的状态。某些类型的 RF 晶体管(尤其是双极型晶体管)会表现出输出功率对输入负载的显著依赖性。在实际测试中,要区分真正的 "源牵引" 效应与输入匹配变化导致的增益变化,并不容易。那些表现出最显著源牵引效应的器件,通常工作在接近其最大可用频率的状态下,而这种情况最好通过采用更高频率的工艺技术来避免。
- 负载牵引时一般尽量保持源端处于匹配状态,减少对负载端的干扰,且保持系统尽可能处于最优状态。
硬件本身会在第 12 章中进一步讨论。图 2.3 展示了一个典型的负载牵引数据集。根据测试的复杂程度、设备的昂贵程度以及投入的时间不同,获取这样一组数据可能需要几天、几小时,甚至几分钟。测试结果呈现为封闭的"等值轮廓线",这些轮廓线标记了满足特定输出功率水平的边界。对于大多数实际应用的 PA 设计者而言,最重要的是 1 dB 与 2 dB 轮廓线,它们表示相对于该频率下器件最大(或最佳)输出功率的水平。
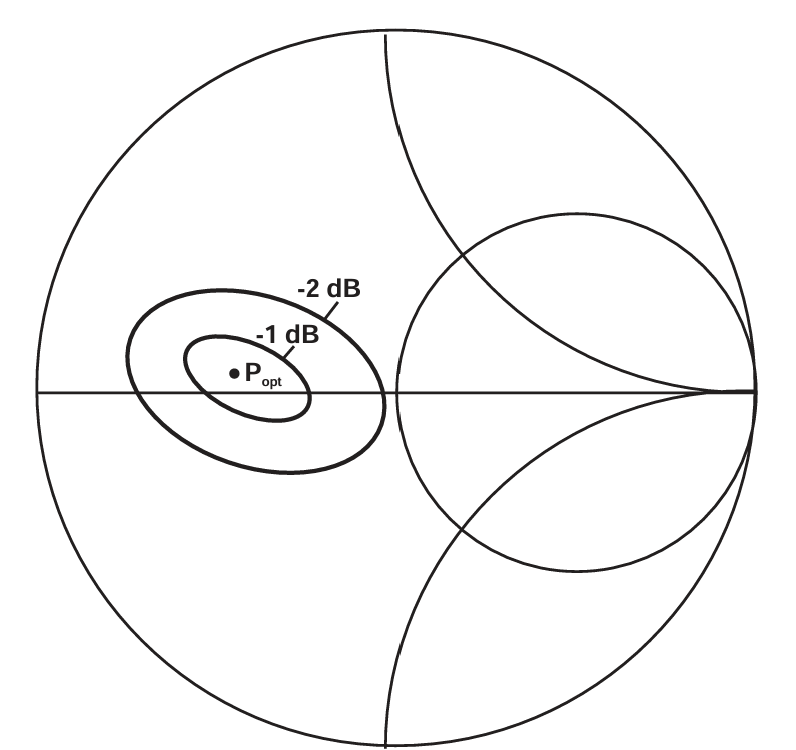
图2.3 Typical load-pull data.
观察图 2.3 中的数据,可以得出最明显的结论是绘制在史密斯圆图上的等功率轮廓线并不是圆形的。与噪声圆或线性失配(增益)圆不同,它们无论设备如何精心校准,都不呈现圆形。多年来,人们把它们比作鸡蛋、土豆、橄榄球......但绝不是橙子或足球。过去一般认为这是非线性行为的表现,但有一个细节长期未被注意:即便将功率衡量标准换成最大线性功率(例如图 2.2 中的 A、A′ 点),这些轮廓的形状仍然大体保持一致。这暗示其非圆形的原因有更直接的解释,将在 2.5 节详细讨论。
负载牵引数据长期以来一直是 RF(尤其是微波)功率放大器设计的基础。它为设计者提供了一个明确的 目标阻抗,用来指导匹配网络的设计策略。它看似将一个难以处理的非线性问题,转换为可以使用线性技术,甚至线性仿真器来解决的问题。随着高性能、快速的非线性仿真器以及逐步改进的大信号模型的出现,人们合理推测:负载牵引设备可能会逐渐像计算尺或干线波导一样被淘汰。但目前来看,这还远未成为现实。事实上,对任何仿真器最严格的验证,就是执行一次 "虚拟负载牵引"。而这种比较(通常需要本不愿合作的双方大量协作)得到的结果顶多算是"还可以"。因此,负载牵引测试在未来仍可能是获取数据、建立并优化 RF 功率器件非线性模型的核心手段。
2.4 Loadline Theory
早在 1983 年,也就是非线性仿真 CAD 工具普及之前,人们就已经展示过,最基本、最初级的 负载线原理可以推广,用于预测在微波频率下、器件保持在线性范围内时的 负载牵引轮廓[1]。这种新颖且极其简化的观点对 GHz 功率放大器的设计产生了重大影响。最大惊喜在于,当把这些理论结果绘制在史密斯圆图上时,得到的轮廓竟然恰好是等电阻圆与等电导圆的交叠区域,呈现出一种"尖角"的外形,与实际 load-pull 测量中常见的那种扁平的轮廓非常相似 。图 2.4 给出了典型结果,直接比较了理论预测与真实测量。在之后的多年里,许多学者尝试改进该理论,去掉原始分析中的一些理想化假设[2]。然而,总体来看,原始方法的简单性依然保留下来,并仍然是 PA 设计时非常有价值的先验设计手段,可用作设计迭代的起点。
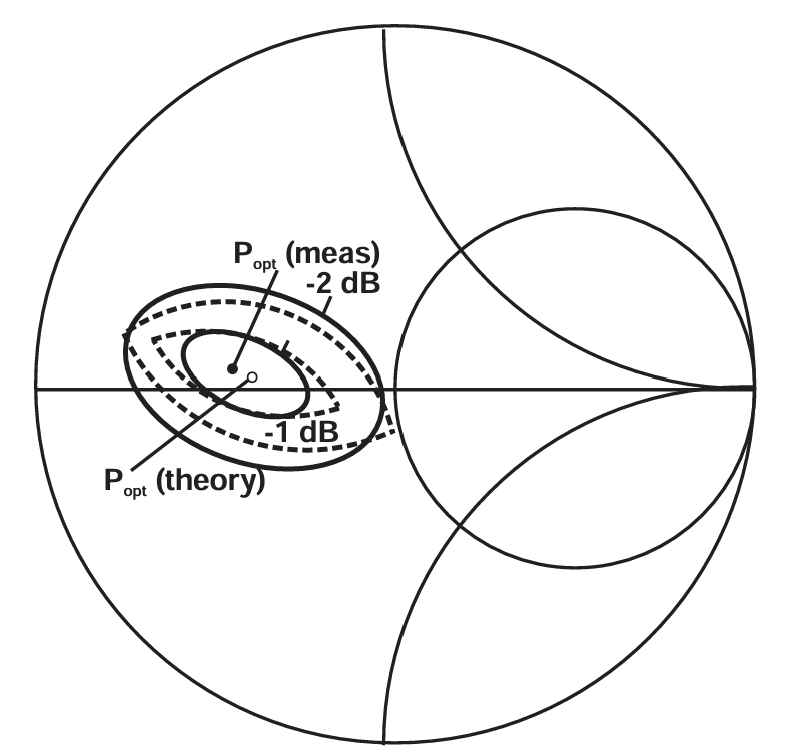
图2.4 Direct comparison of experimental (solid lines) and theoretically generated power contours (dotted), using the loadline analysis and equations in this section [1].
对 RF 功率放大器的分析,始于一个高度理想化的元件模型,如图 2.5 所示。这是一个强非线性的理想跨导器件,用"电压控制电流源"表示,且具有零输出电导和零开启电压。跨导在输入阈值以下出现截断非线性以及电流在 Imax 处出现硬饱和,除了截断与饱和,这个器件在其他范围内被视为线性。该分析的关键是器件始终不允许突破其线性工作极限。换句话说,本分析只适用于增益压缩开始出现之前的区域。
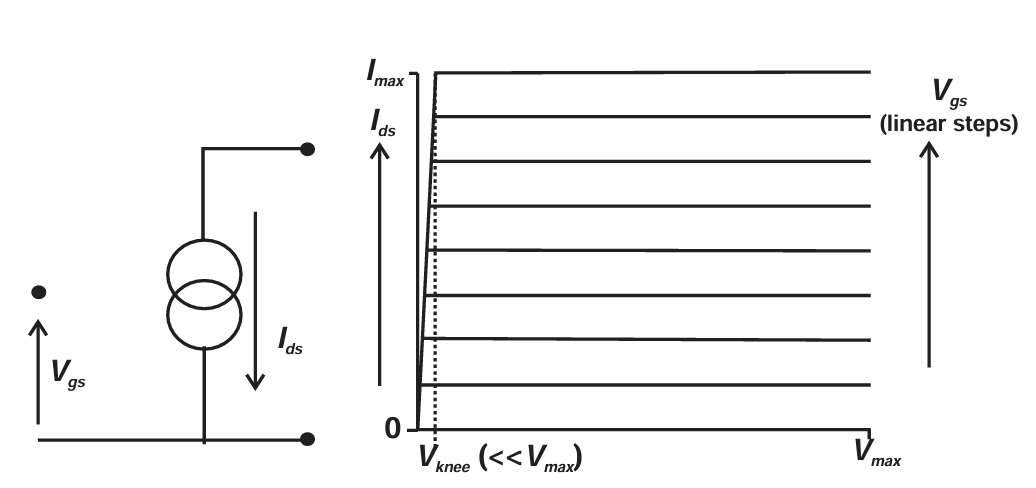
图2.5 Ideal strongly nonlinear device model. The "knee" turn-on region is neglected, and between 0 and Imax, the output current generator is linearly controlled by the input generator.
图 2.6 进一步展示了用于分析该理想器件的 RF 电路。输出(漏极)通过 交流耦合连接至 RF 负载。直流偏置通过一个 RFC(射频扼流圈) 提供,且 RFC 在工作频率处的阻抗非常高。一个重要的细节是尽管晶体管被视为一个理想的压控电流源,射频负载会含有一定的无功分量,而晶体管的输出寄生参数被视为负载的一部分。
假设读者对负载线匹配概念已足够熟悉,我们可以直接观察图 2.6 的 RF 波形,其中的设备工作于正弦激励和最佳负载的条件下。电流在其最大线性范围内摆动,从 0 到 Imax,摆幅为 Imax/2。电压在其最大范围内摆动,从 0 到 2Vdc,摆幅为 Vdc。显然,在这个最佳功率匹配的条件下,负载线对应的电阻值为
R o p t = V d c / ( I m a x / 2 ) = V d c / I d c R_{opt}=V_{dc}/(I_{max}/2)=V_{dc}/I_{dc} Ropt=Vdc/(Imax/2)=Vdc/Idc
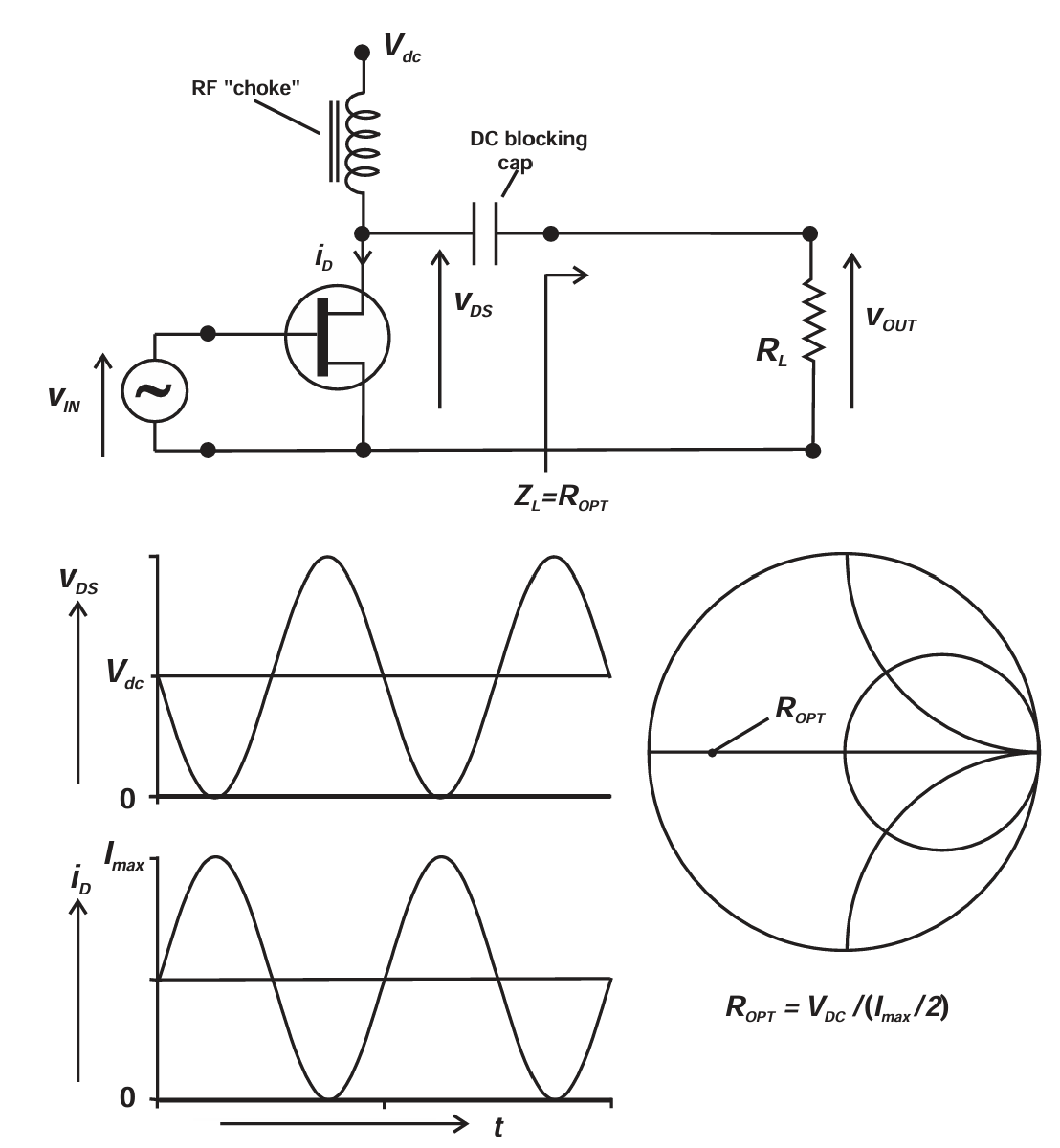
图2.6 Class A linear power amplifier, with optimum loadline match.
这是电子学中最基本、最初级的结果之一,这里并没有试图"重新发明"什么。然而,我们在此做了一个重要假设,即RF 频率下的电流和电压轨迹,与在直流曲线示波仪上观察到的轨迹一致。这个问题长期以来一直存在争论[3],并且已经被半导体设备制造商广泛研究与讨论[4]。但在此处,我们仍然将这一 准静态假设与之前其他理想化条件一并采用。此外值得注意的是,峰值 RF 电压 2Vdc 主要源自我们假设的正弦波形的对称性。一个以其平均值为对称中心的 RF 正弦波,为了在波形下半周期仍保持在零电压以上,其峰值电压必须达到2倍 DC 电源电压。我们将在后面看到,当波形因谐波成分而变得不对称时,峰值电压可以大于或小于 2Vdc。
图 2.6 显示了器件在最佳匹配条件下的工作情况,此时它将输出 RF 功率
P o p t = ( 1 / 2 ) ⋅ V d c ⋅ I d c P_{opt}=(1/2)\cdot V_{dc}\cdot I_{dc} Popt=(1/2)⋅Vdc⋅Idc
这对应于一个传统的 Class A 线性放大器,其漏极效率为 50%。
现在,我们可以利用这一简单的模型与电路,通过偏离最佳电阻负载 Ropt+j0 来改变 RF 负载的电阻和电抗分量,以描绘一个负载牵引轮廓。特别地,我们将确定一组负载,使其输出功率为 Popt/p 。其中,p = 2 用于初步的清晰说明。
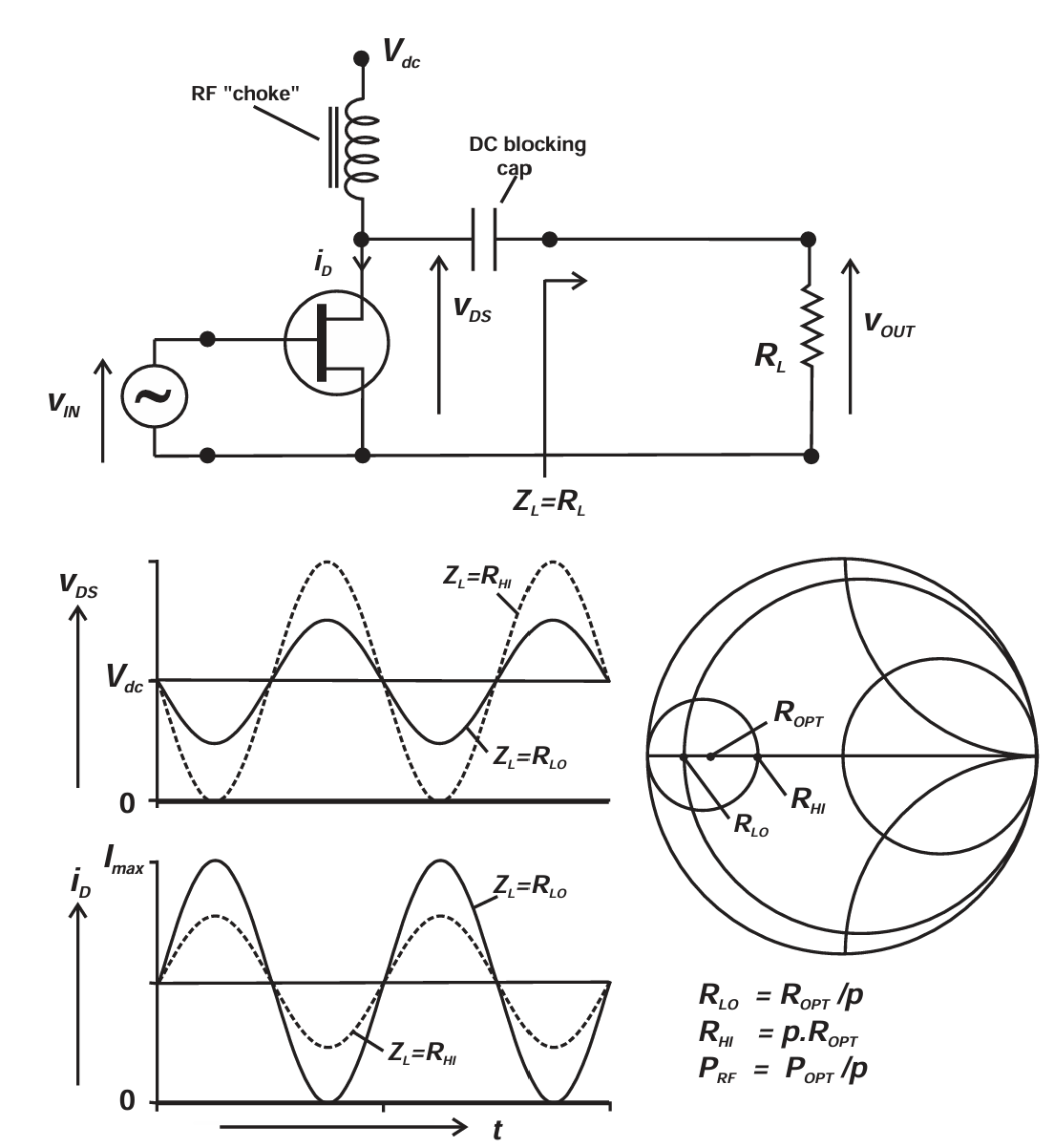
图2.7 Class A linear power amplifier case 1: resistive output loads for RL<ROPT; RF power output is POPT/p (Ipk=Imax). For RL>ROPT, RF power output is POPT/p (Ipk=Imax/p).
图 2.7 显示存在两种纯电阻负载会使最大线性输出功率变为 Popt/p ,即 Ropt/p 和 pRopt 。对于较小电阻负载 Ropt/p ,器件可以在完整电流范围内摆动(0 到 Imax),但电压摆幅仅为 2Vdc/p ,所以输出功率为 Popt/p 。对于较大电阻负载 pRopt ,为避免电压摆幅超过最大线性范围 2Vdc ,驱动必须减少。电流幅度必须按比例减小为原来的 1/p ,因此输出功率同样变为 Popt/p 。
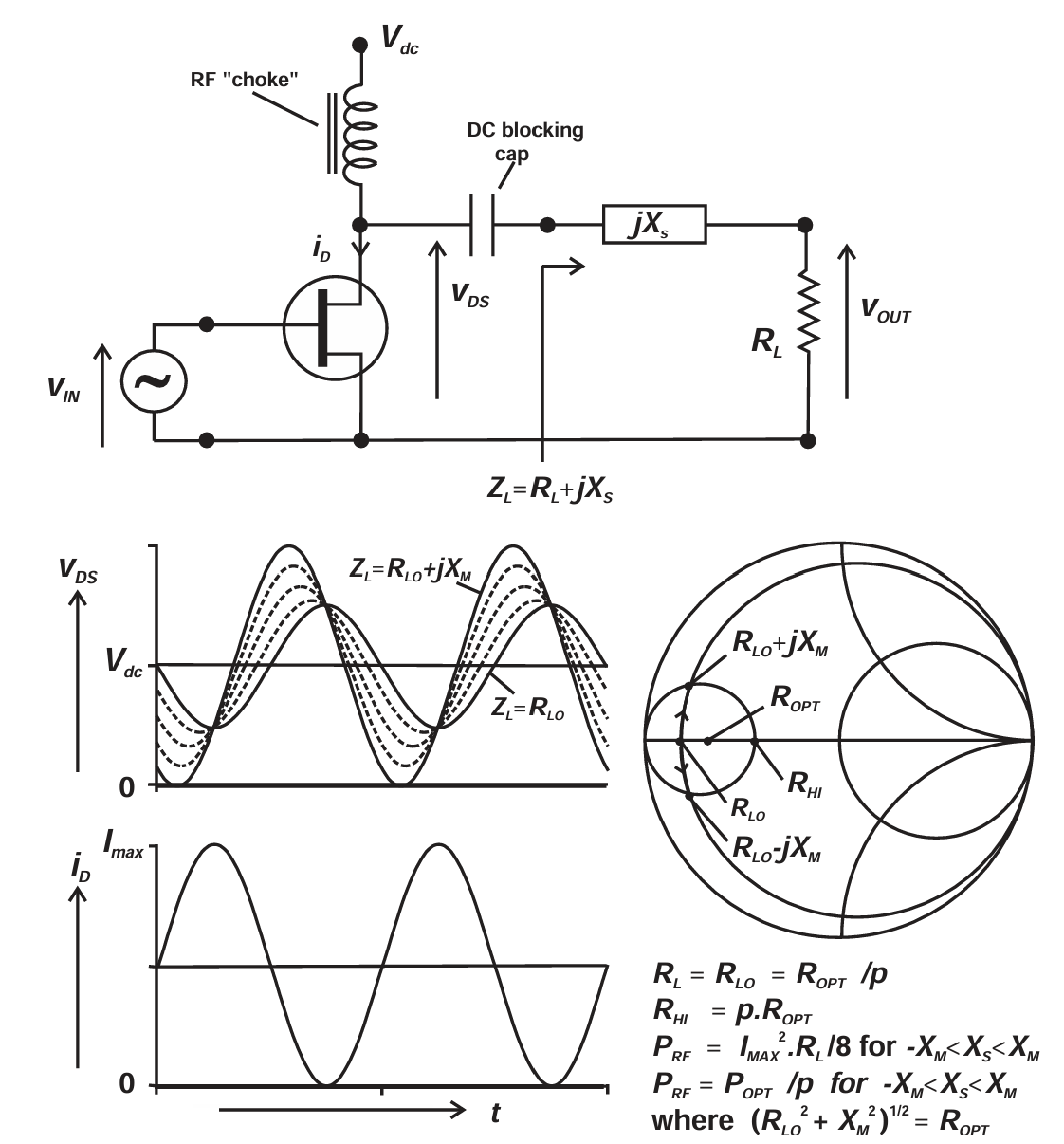
图2.8 Class A linear power amplifier case 2: output load resistive component lower than ROPT. For RL=ROPT/p, RF power output is POPT/p, over a range of series reactance---XM<0<XM.
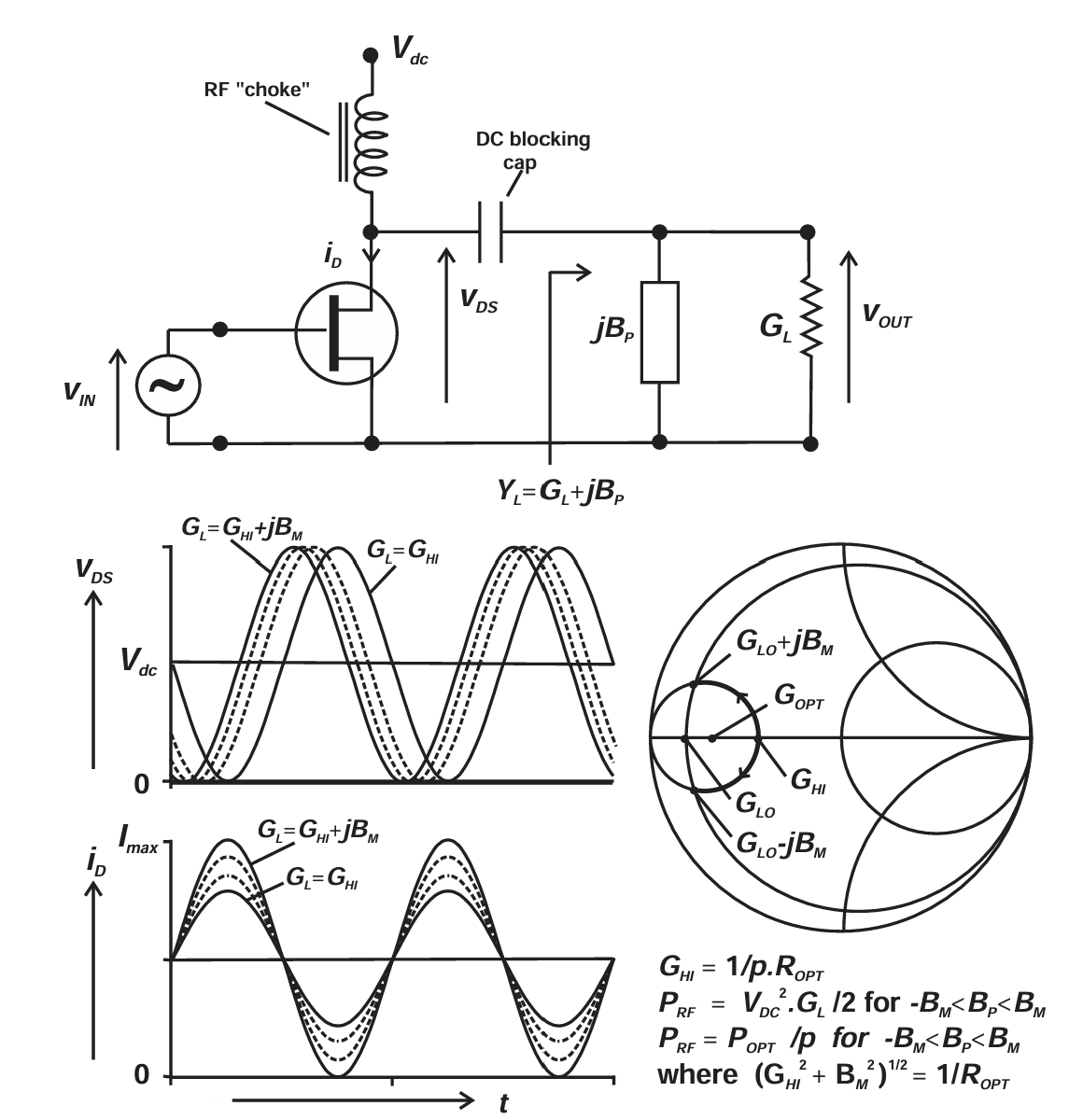
图2.9 Class A linear amplifier case 3: output load resistive component higher than ROPT. For RL=pROPT, RF power output is POPT/p, over a range of shunt susceptance---BM<0<BM.
因此,对于输出功率水平为 Popt/p 的负载牵引轮廓,我们已经得到两个点。图 2.8 展示了若在负载电阻上串联一定量的电抗,则可以将 Ropt/p 这一点扩展成一段连续的等功率弧线。关键在于当电流摆幅保持在其最大允许值时,通过加入串联电抗可以提高本来较低的电压摆幅,而不改变功率输出 。这种串联电抗具有一个最大值 ±Xm ,该值可以使串联组合 Ropt/p ± jXm 的复阻抗幅值等于 Ropt 。类似地,图 2.9 显示若在负载电导上并联一定量的电纳,则可以将 pRopt 扩展为另一段等功率弧线。在这种情况下电压摆幅保持在最大允许值 2Vdc,而电流摆幅则可增加,通过对应地增加一个并联电纳 。其极限情况是该负载的复导纳幅值等于 1/Ropt (= Gopt)。
这两段等功率弧线恰好分别沿着印刷式 Smith 圆图上的等电阻圆(R = Ropt / p)和等电导圆(G = 1/(pRopt))继续前进。剩下要证明的是,整个轮廓确实是封闭的,并且这两条弧线的终点在其交汇处重合。所需做的仅是证明 阻抗Ropt/p + jXm 与导纳 1/(pRopt) + jBm 表示的是同一个阻抗,其中
X m 2 = R o p t 2 ( 1 − 1 / p 2 ) B m 2 = G o p t 2 ( 1 − 1 / p 2 ) X^2_m=R_{opt}^2(1-1/p^2) \\B_m^2=G_{opt}^2(1-1/p^2) Xm2=Ropt2(1−1/p2)Bm2=Gopt2(1−1/p2)
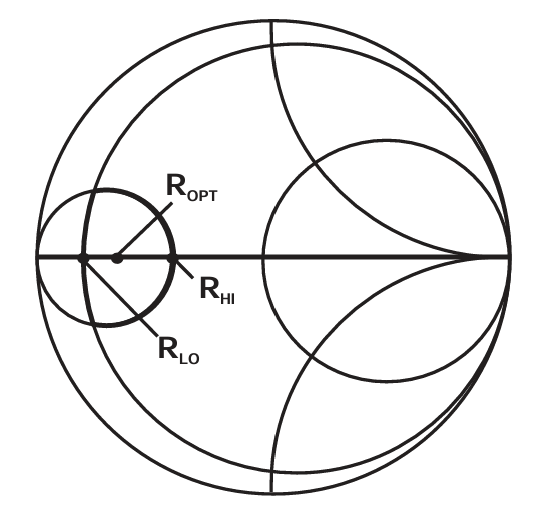
图2.10 Constant power contour for p = 2 (--3 dB). Closed contour is formed by intersecting circles of constant resistance (R = RLO = ROPT/p) and constant conductance (G = 1/RHI = 1/pROPT).
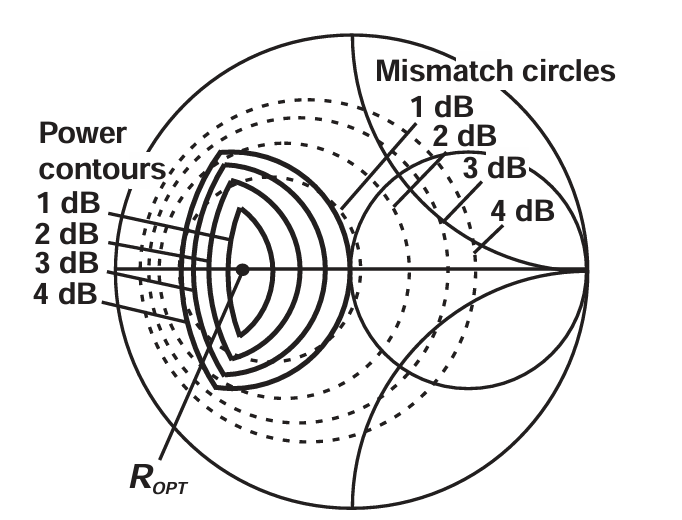
图2.11 Power-match contours (solid, 1 dB to 4 dB contours shown), compared with gain mismatch circles (dotted) based on a source impedance equal to the optimum power match (ROPT = 20Ω).
对于 p = 2(即 3 dB 功率轮廓)的最终结果如图 2.10 所示。等功率轮廓明显呈非圆形 。图 2.11 展示了一组等功率轮廓,它们可以用上述方法轻松构建,对应不同的 p 值(每个 p 间隔代表约 1 dB)。特别值得注意的是,1 dB 等功率轮廓所覆盖的目标区域非常小,而传统的、以 Ropt 为中心的 1 dB 失配圆(图 2.13 虚线部分)则大得多 。这说明功率匹配并不是 s22 在大信号条件下发生简单移动的结果。
- 等功率轮廓是等电阻圆与等电导圆的交汇部分,呈现明显的非圆形,尺寸面积也比较小。
- 等功率圆与失配圆不一致也说明了在PA设计时,可以将s22作为一个参考,但不适合以s22为检验标准,即使相同的失配情况,输出的功率不一定会相等。
这些如图 2.10 和 2.11 所示的等功率轮廓适用于任何频率。这对那些习惯于看到测量轮廓随频率显著变化的负载牵引从业者来说,多少会有些出乎意料。关键在于阻抗测量参考面的选择。本节中,参考面设定为晶体管输出电流源的端口,而实际中最接近的可测量物理点位于芯片和封装寄生电抗之外 。从另一角度来看,这可以理解为此处分析的轮廓所代表的阻抗是以绝对的电阻和电抗(单位为欧姆)来测量的。因此,只要外部电路在任意频率下被分析,其结果都可以与这些负载牵引轮廓一起绘制在同一张图上。如果参考面被移动到某个点,使得电流源与参考点之间包含了具有特定数值的寄生电抗,那么轮廓将变得依赖于频率,因为电容、电感和传输线都具有随频率变化的电抗。为了将本节推导的理论结果与实际测量数据进行比较,就有必要执行这种"去嵌入"操作。尽管如此,通过选择合适的参考面位置以消除负载牵引轮廓的频率依赖性,仍然是一项非常有用的特性。第 2.6 节将说明这一点在宽带设计中尤为有价值。
- 上述负载线操作的参考面设置在晶体管输出端口,因此不存在寄生分量(也基于前面的理想化模型和假设),使得结果可以适用于任何频率;但是实际测试中由于封装等原因,寄生电抗会导致不同频率下有不同的负载线,甚至不同输入功率下也会有不同结果。
2.5 Package Effects and Refinements to Load-Pull Theory
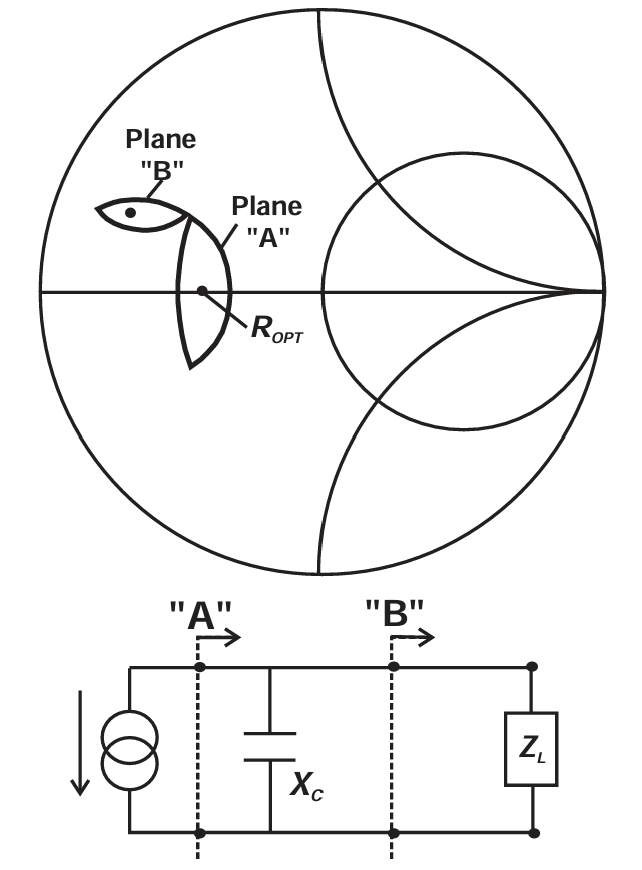
图2.12 Power contour measured at reference plane A (transistor current generator) and plane B, showing the appropriate compensation (de-embedding) required at B due to the shunt capacitance. Contours plotted for ROPT = 20Ω, XC = 35Ω (5 pF at 2 GHz).
上一节中建立的基本负载牵引理论需要进行扩展,以便能够与测量数据直接比较。图 2.12 展示了典型情况下的问题。负载牵引轮廓是在 A 面(晶体管电流源端口)推导的,我们需要将该结果转换到 B 面,即封装芯片的输出焊盘处。为了在 B 面呈现一个能够映射回 A 面原始轮廓的阻抗,需要考虑器件输出电容、键合线电感以及封装寄生参数 。这对于线性电路仿真器而言是简单的任务,但需要谨慎应用这些变换。例如,图 2.12 显示了在 B 面的变换,其中唯一显著的寄生元件是并联电容。在从 A 面转换到 B 面的过程中,轮廓似乎绕着并联电导圈旋转或滑动。但方向与阻抗变换相反,因为这里我们是在补偿或去嵌入该并联元件。如果电容值固定,那么这种变换显然是随频率变化的。图 2.13 显示了在典型晶体管及封装结构中,随频率应用必要变换后的效果。
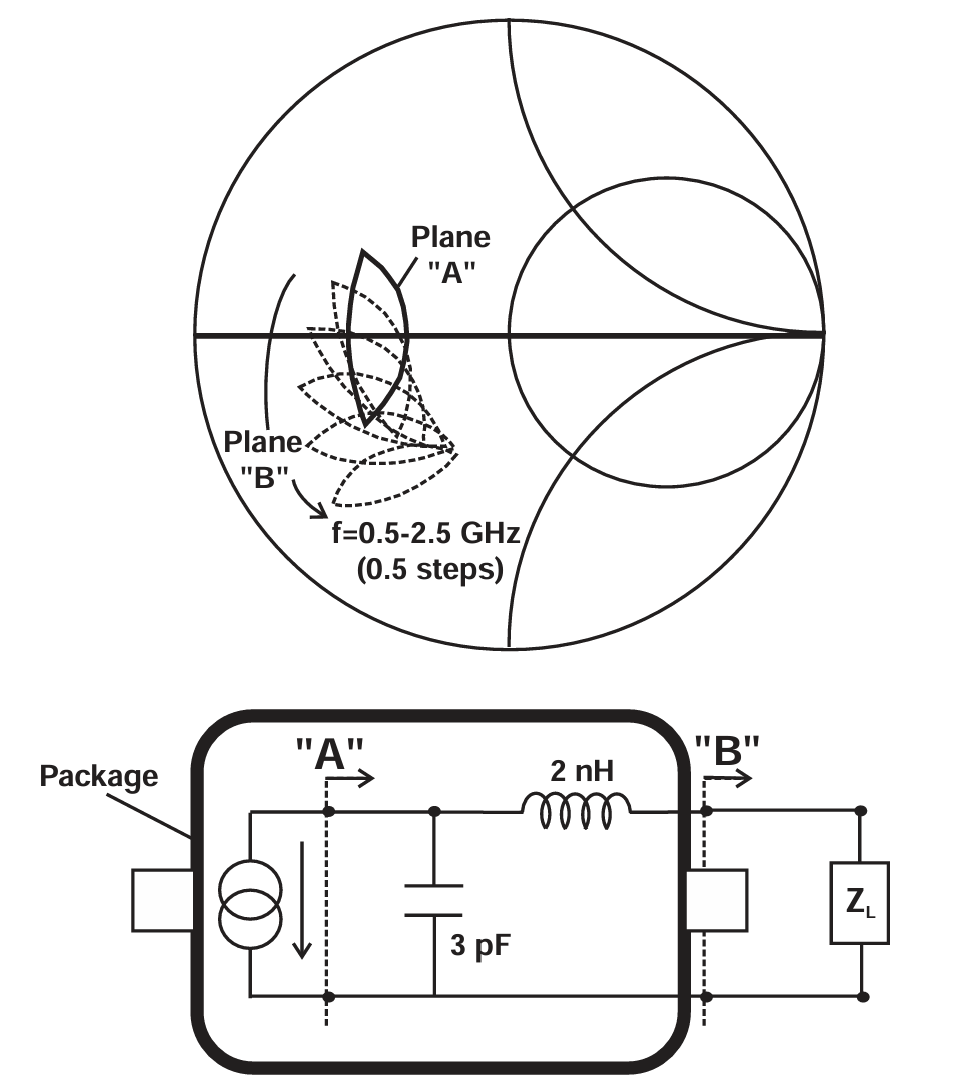
图2.13 Power contour measured at reference plane A (transistor current generator) and plane B for a typical set of package parasitic reactances.
- A面并联一个电容到B,因此从B面映射回A面需要去除并联电容,即沿着等电导圆逆时针旋转。映射时需要注意旋转方向。
回到图 2.4 可以看到,理论轮廓(虚线)按上述方法经过串联键合线电感和输出电容的补偿,因此从原本直立的位置向后倾斜。图 2.4 中理论与测量结果吻合良好,一般经验也表明负载线理论往往会给出稍微更严格的设计目标区域,这对实际设计来说是可以接受的。
- 等电阻圆与等电导圆重叠处是垂直于实轴的,因为通过串联键合线电感和输出电容的补偿,才会使得发生角度偏移。
有人认为,通过将设计阻抗参考面转换到 A 面以消除频率依赖性是多此一举,因为器件与封装寄生参数可能并不准确。这在无线通信频段常见的窄带设计中特别适用。从原则上讲,单一频率的测量负载牵引数据集可以完成设计,但无法分析不同匹配网络随频率变化的性能,即便对窄带设计来说,这也是严重的限制。第 2.7 节的设计例子还将展示,理论负载牵引轮廓方法能进行一些有用的容差分析,而单一数据集无法做到。基于多种原因,了解封装寄生参数是良好的射频设计实践。可靠的器件厂商应能提供封装模型;在极端情况下,对于 2 GHz 以下的频率,简单封装模型也不难推导。一种方法是使用裸片的 S 参数(如果可作为独立产品提供),并将简单的封装模型拟合到封装器件的数据上。
尽管图 2.4 中理论与实测数据的总体一致性很好,但在将该方法用于实际功放设计时,仍有一些改进是建议采用的。最明显的是需要重新审视 Ropt 的计算。回到图 2.6,可见在器件 RF 电流达到峰值 Imax 的瞬间,漏极电压为零。这显然直接来源于图 2.5 所示的理想导通特性。为了维持栅极控制的电流,有必要降低负载电阻值,使漏极(或集电极)电压始终高于所用器件的相应拐点电压。对于 BJTs、HBTs 和 GaAs FETs,一个合适的电压修正值 Vk 为 1 V。LDMOS 器件则需要更大的修正量,但它们也会在更高的电源电压下工作。
对峰值电流 Imax 也需要做一些更正,它并不是数据手册中常见的参数。事实证明,Imax 并不是一个容易直接测量的参数。估算其值的最佳方法是搭建一个优化的 A 类放大器并观察直流电源电流。如果假设射频电流为正弦波,那么 Idc 的值将等于 Imax / 2。大多数数据手册会给出典型的 A 类工作条件,包括射频输入、输出功率以及直流偏置,因此可以得到一个代表性的 Imax 值。该方法对双极型晶体管特别有用,因为相比 FET,它们没有明显的电流饱和特性。因此,修正后的 Ropt 为:
R o p t = ( V d c − V k ) / I d c R_{opt}=(V_{dc}-V_k)/I_{dc} Ropt=(Vdc−Vk)/Idc
某些 FET,尤其是 MESFET,在 I--V 特性上呈现显著的斜率,对应于直流输出电导。因此,可能会倾向于将其视为一个与外部负载电阻并联的物理电导。然而在实际中(并且可以通过运行非线性时域仿真进行验证),随着器件在负载线上的电流和电压范围内摆动,直流特性的斜率往往会被抵消,而假设交流输出电导为零通常比简单的直流电导修正能给出更好的近似。
这种处理方法是一种近似,也是一个有用的起点。使用对完整 I-V 特性做了精确拟合的非线性仿真器,是获得 Ropt 精确最优值的唯一途径。而精确值与近似值之间的差异往往落在晶体管电流/阈值规格的全局变化范围之内。
2.6 Drawing the Load-Pull Contours on CAD Programs
尽管负载线(方法在功放设计中因其简洁性而在微波放大器领域广受欢迎,但 CAD 软件开发者并未如此迅速地接受这一概念。如果在任意线性 RF 或微波电路分析程序中加入一个简单的功能,使其能够根据少量器件参数输入绘制负载牵引等高线,就像通常提供噪声圆那样,那将是非常有用的。幸运的是,要"欺骗"一个简单的电路分析程序,使其绘制出这些等高线,其实非常容易。
在图 2.10 中,很明显负载牵引等高线的两个弧段可以用串联和并联 LCR 电路来建模 。可以选择这些组件的取值,使得在针对特定设计所使用的频率扫描范围内,这些"虚拟"电路的阻抗正好覆盖目标区域,从而定义每个等高线的实际边界。图 2.14 显示了构建这些电路的方法,并给出了元件值与所需等高线(以 dB 表示)以及频率扫描范围之间关系的公式。显然,当扫描范围改变时,这些元件的取值也必须随之改变,但大多数 CAD 软件都允许将元件的值定义为依赖于频率范围或电路内其他元件值的表达式,因此这使得绘制等高线基本上可以独立于频率扫描设置。
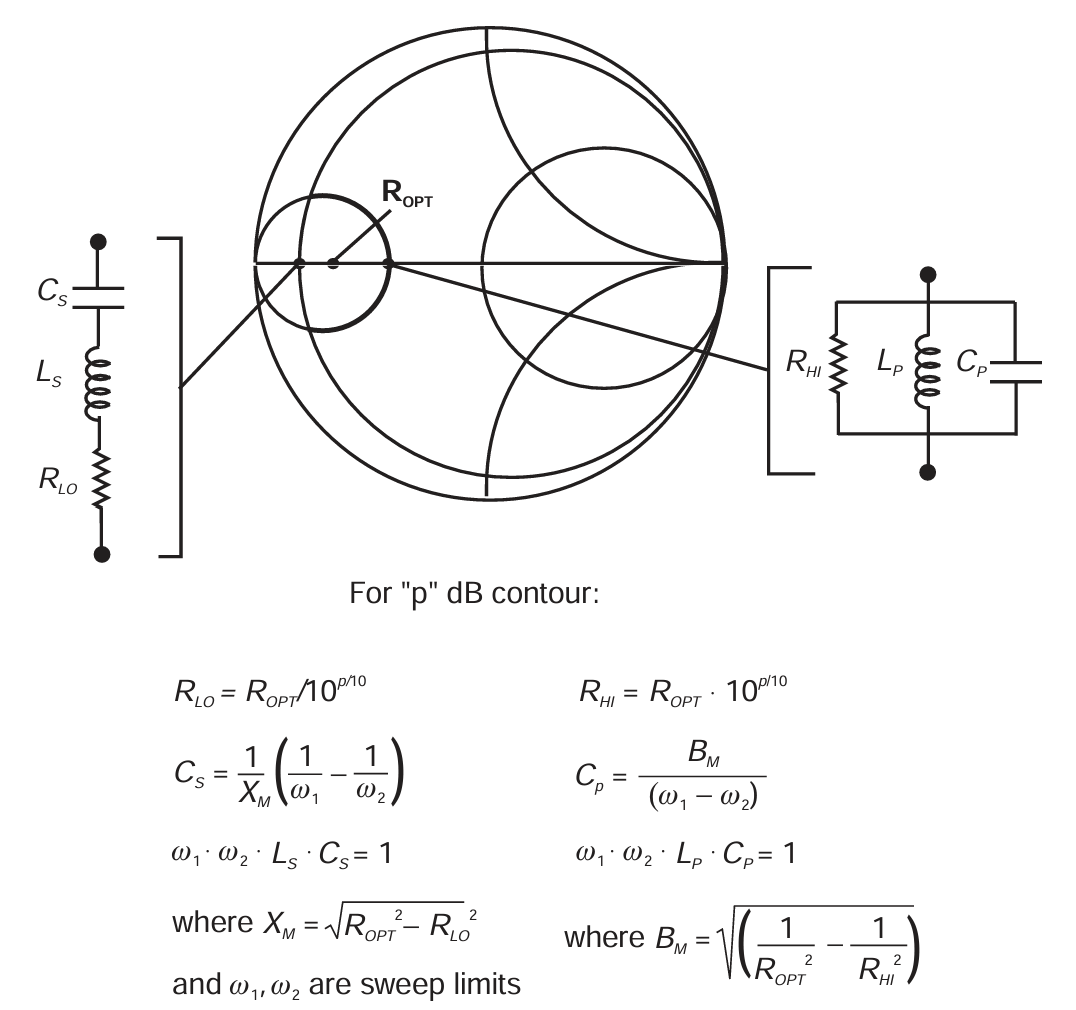
图2.14 Construction of load-pull contours on linear circuit analysis programs by use of dummy series and parallel resonant circuits for series and shunt arcs.
2.7 Class A Design Example
现在将通过一个设计示例来展示使用前几节所发展的技术来设计 A 类放大器的基本步骤。如本章开头所述,这里的目标是将一个具有挑战性的非线性设计问题,转化为一个可以使用最基本设计工具解决的问题。该过程类似于经典的低噪声放大器设计,其中输入阻抗变换基于对最佳噪声匹配点以及噪声圆族的了解。而在这里,输出匹配网络完全基于负载线方法,以及由此得到的 Smith 圆图中 1 dB 负载牵引等高线的构建。输入匹配使用线性 S 参数来完成;设计基于一个接近但未超过可测得增益压缩点的功率水平,在该点 S 参数仍然接近低功率水平下的测量值。前面已经指出,在这一点获得的良好功率匹配很可能也接近于更高压缩程度下的最佳匹配,且无论如何,对于具有包络变化的信号来说,这代表了线性性能的良好折中。
该设计基于一个典型的 1 瓦 GaAs MESFET,工作频率为 1.9 GHz。这是一个 A 类设计;因此最终设计无法满足蜂窝手机功放的效率要求,但用于说明目前已讨论的设计原理非常合适。
步骤1:确定目标规格、选择器件、计算 Ropt
在本例中,选择了一颗在其 1 dB 压缩点可提供典型 29 dBm 输出功率的晶体管。厂商数据表显示,该功率是在 4.8 V 的 A 类直流偏置和 375 mA 的电流下获得的。设计频率范围为 1.75--1.85 GHz。
考虑到典型 GaAs MESFET 的导通电压约为 1 V,由式 (2.2) 可得:
R o p t = ( 4.8 − 1 ) / 0.375 = 10.1 Ω R_{opt} = (4.8-1)/0.375=10.1Ω Ropt=(4.8−1)/0.375=10.1Ω
步骤2:搭建电路图并确定输出匹配拓扑,使在 A 面呈现 Ropt
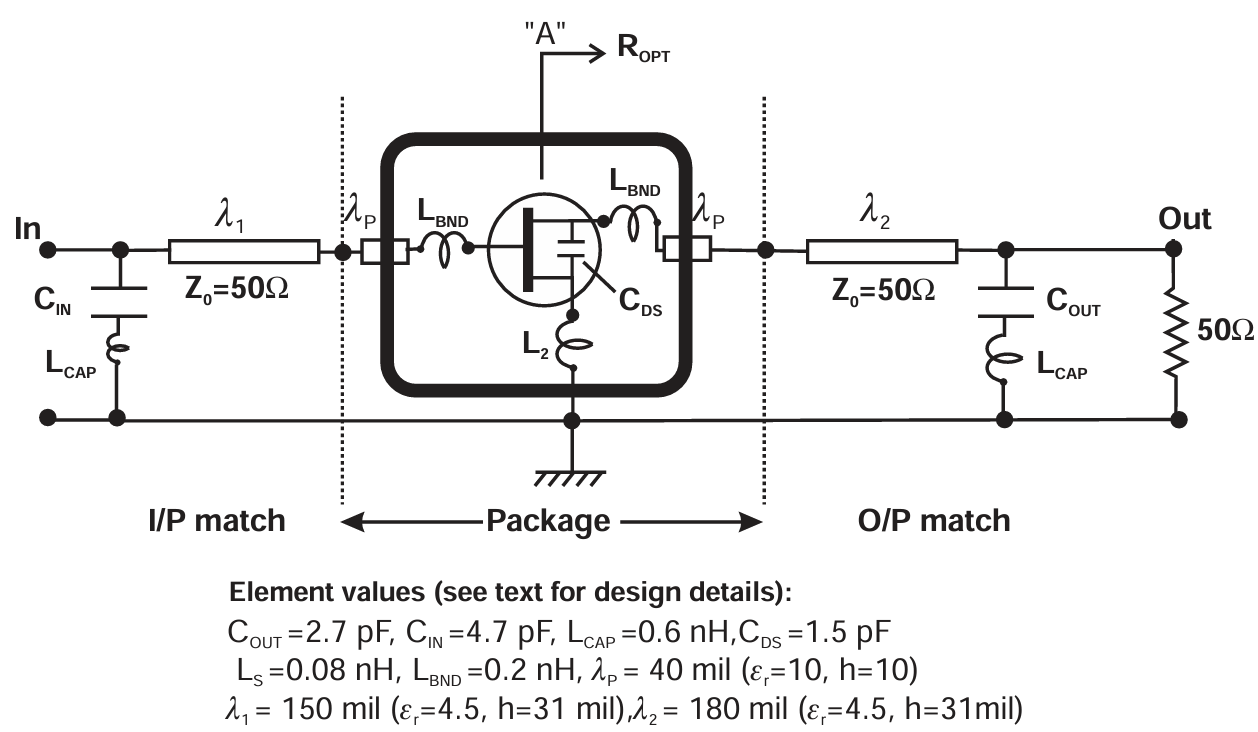
图2.15 Schematic of 1.9 GHz 1-watt linear PA design.
参考图 2.15,我们假设晶体管输出电容及封装寄生参数已知。因此匹配问题就是要在 A 面(位于封装内部、并包含器件输出电容的参考面)呈现 10.1 Ω 的阻抗。初始匹配策略是在中频点呈现最佳阻抗,然后执行扫频分析以确定满足规范的工作带宽。示例中采用了一个简单的低通结构,由一段 50 Ω 微带线和一个并联电容组成。这些元件的数值可以调整以在中频获得合适的匹配,如图 2.16 所示。注意,1 dB 功率轮廓是按照第 2.6 节所述方法绘制的,使用串联和并联谐振的虚拟电路元件在仿真文件中实现。
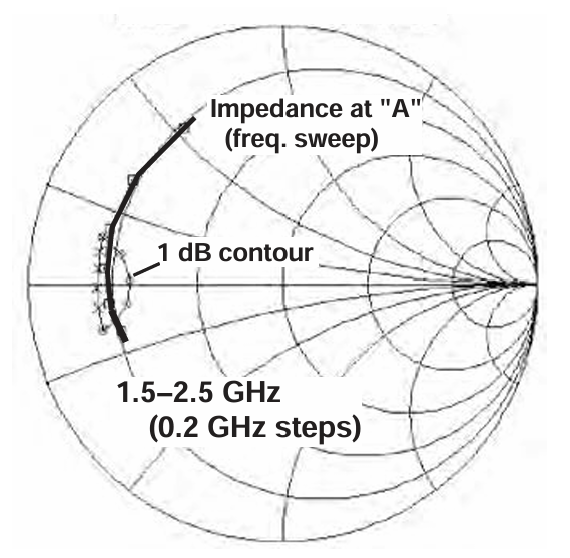
图2.16 Plane A impedance sweep, with 1 dB power contour (single-section matching network).
观察宽带扫频结果可以看到,尽管该匹配拓扑本质上是窄带型的,但对于本应用而言,其小百分比带宽仍然是足够的。图 2.17 显示,如果需要,通过使用双节匹配网络可以获得更大的带宽;整个 1.5 到 2.5 GHz 的频段都表现出良好的功率匹配,且落在 1 dB 等高线之内。此类匹配使用了额外的元件,对于典型的无线通信带宽可能属于过度设计。然而,它清楚地展示了双节网络在带宽上的改善,同时也显示了"Plane-A"负载牵引参考平面技术的实用价值。这些匹配网络将在第 5 章进一步讨论。
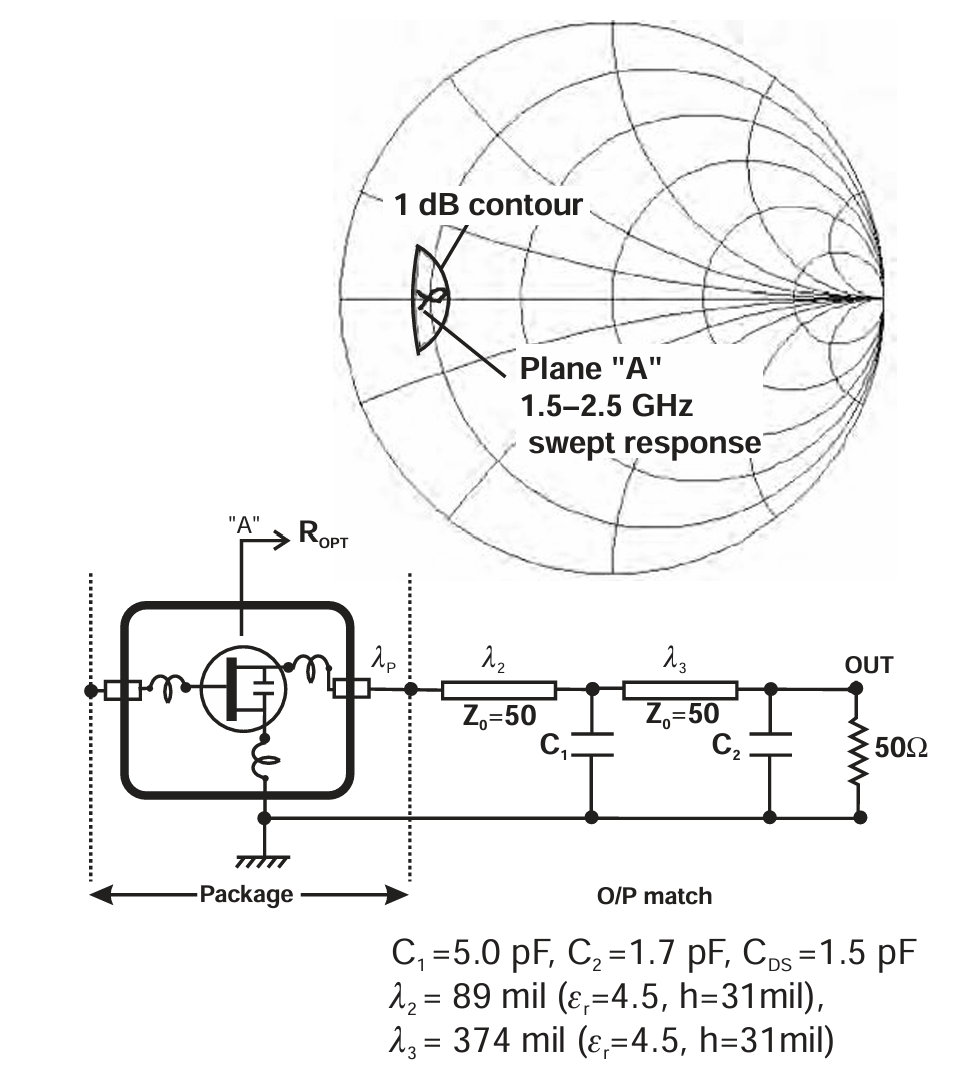
图2.17 Broadband power match (matching capacitor parasitics not included).
单节匹配网络可以用一段微带线和一个贴片电容来实现。典型的表面贴装(SMT)电容器,即使是 0402、0201 这样的微型封装,在 2 GHz 也会具有显著寄生效应,必须在电路仿真中体现出来。在本例中,加入了 0.6 nH 的串联寄生电感。对于这种窄带设计,该寄生的作用仅仅是将原本设计的电容值从 4 pF 降低为 2.7 pF 的等效值。然而,在宽带设计中,这种简单处理将不再适用,可能需要选择寄生更低的元件。在此阶段,值得对器件和制造公差进行初步检查。
由于这是功率放大器,最重要的问题之一是:在输出端的两个关键匹配元件(电容和微带线)存在制造公差的情况下,输出功率会变化多少 。假设微带线宽度和基板介电常数能够严格控制,则电容值和微带线长度(即其具体定位)可能会变化达 ±10%。显然,公差越大,成本越低,产率越高。图 2.18 显示了当输出匹配电容 Cout 和微带线节长 λ/2 发生 ±10% 浮动时,A 面的阻抗变化。尽管该范围(阴影区域)在本例中仍然落在 1 dB 等高线内,但也能看出仍存在更好的设计中心点。能够同时观察频率和元件公差下的输出功率变化,是这种简单设计技术的一个强大且未被广泛认识的优点。
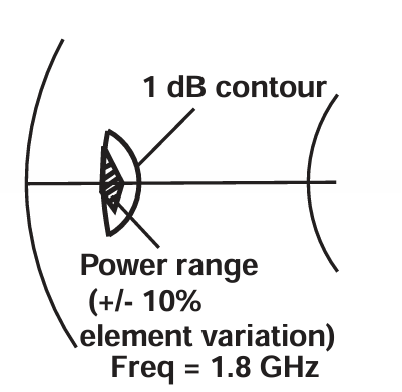
图2.18 Power variation due to manufacturing tolerances on output matching elements.
步骤 3:使用线性(S 参数)方法设计输入匹配
在已经完成输出侧的最佳功率匹配设计后,现在可以使用标准的线性技术完成输入匹配的设计 。由此得到一个类似的单节低通输入匹配网络,如图 2.15 所示。整个放大器的线性响应可以绘制出来,包括输入和输出 VSWR,如图 2.19 所示。注意,用整体的 s22 来测量的输出 VSWR 较差,回波损耗约为 3 dB。部分原因是输入匹配中存在电抗成分(k 接近 1),但主要原因是输出侧的功率匹配。即使使用有损元件降低输入网络的 Q 值,输出端仍然无法与 50 欧匹配。这实际上就是当前设计与简单线性共轭匹配设计之间的主要区别:后者能提供良好的输出 VSWR,但其最大输出功率可能会低 2--3 dB。
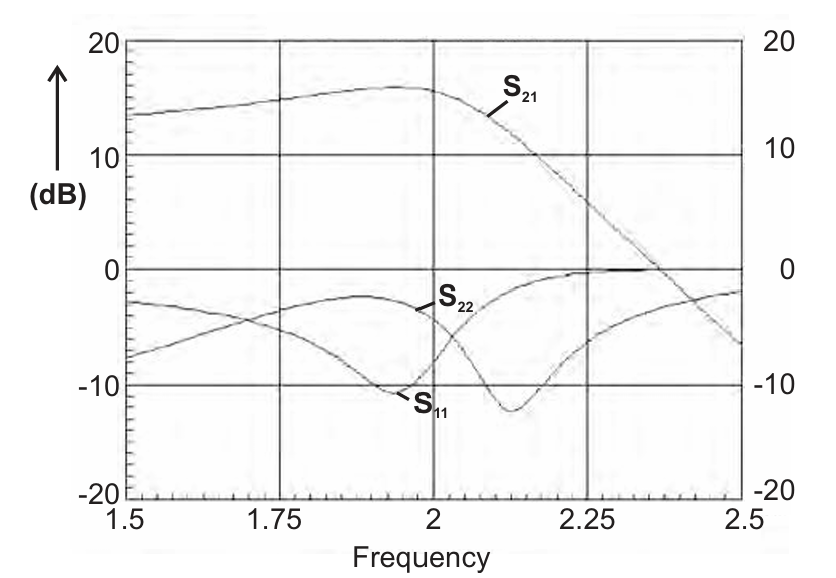
图2.19 Gain and return loss of 1W Class A amplifier.
步骤 4:实际搭建
线性仿真器当然无法给出功率性能的扫描。通常,这时需要使用非线性仿真器对整个设计进行分析,以去除理想化假设,并在实际 PCB 布局之前对设计参数进行微调,这是设计流程的最后一步 。图 2.20 展示了基于上述设计的放大器的一些实测数据。所用的 GaAs MESFET 器件是市场上常见的低成本封装器件。1.8 GHz 和 1.9 GHz 的功率扫描显示其 1 dB 压缩点至少为 29 dBm。在 1.9 GHz 下的功率性能似乎比设计频率 1.8 GHz 略好一些,但整体性能仍在预期范围内。
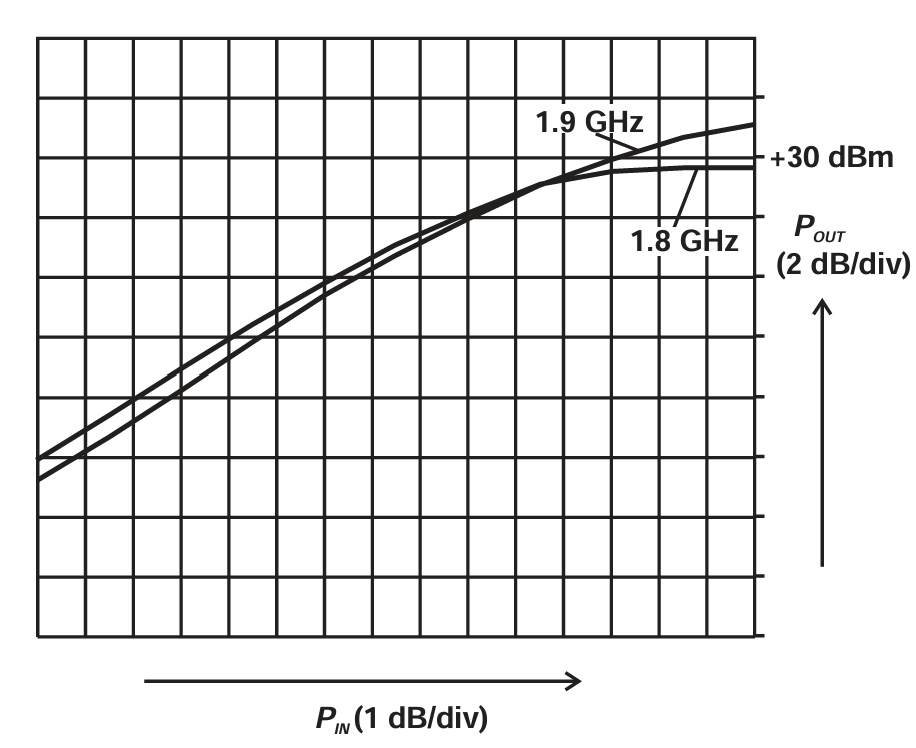
图2.20 Measured swept power data on Class A amplifier design.
2.8 Conclusions
本章表明,通过使用负载线技术来确定最佳功率匹配,Class A 功率放大器的设计可以被简化为一个线性设计问题。尽管本章的内容在某些人看来可能比较基础、近似,但其中描述的基本方法已被用于设计各种射频与微波放大器------从窄带到宽带、从几十毫瓦到几百瓦、从低频直到 100 GHz 以上。对于希望应用这些方法的人来说,建议大胆尝试,不必被第 3 章及之后介绍的更高级概念所吓倒。
参考文献
1\] Cripps, S., "A Method for the Prediction of Load-Pull Power Contours in GaAs MESFETs," Proc. IEEE Intl. Microw Symp., MTT-S, 1983, pp. 221--223. \[2\] Kondoh, H., "FET Power Performance Prediction Using a Linearized Device Model," Proc. IEEE Intl. Microw Symp., MTT-S, 1989, pp. 569--572. \[3\] Barton, T., et al., "Narrow Pulse Measurement of Drain Characteristics of GaAs MESFETs," Elect. Lett., Vol. 23, No. 13, June 1987, pp. 686--687. \[4\] Ladbrooke, P., "Pulsed IV Measurement of Semiconductor Devices," available from Accent Inc., sales@accentopto.com.