LC106 从中序与后序遍历序列构造二叉树

一.任务描述：

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

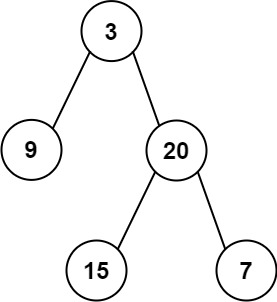
**输入：**inorder = $9,3,15,20,7$ , postorder = $9,15,7,20,3$

输出： $3,9,20,null,null,15,7$

示例 2:

**输入：**inorder = $-1$ , postorder = $-1$

输出： $-1$

二.解题思路:

1. 后序遍历的特点： 最后一个元素是根节点
2. 中序遍历的特点： 根节点左侧是左子树，右侧是右子树
3. 递归构建：

从后序确定根节点

在中序中找到根节点位置

划分左右子树区间

递归构建左右子树

三.代码实现:

复制代码

int post_idx;

typedef struct {
    int key;
    int val;
    UT_hash_handle hh;
} hashTable;

hashTable* idx_map;

void insertHashTable(int x, int y) {
    hashTable* rec = malloc(sizeof(hashTable));
    rec->key = x;
    rec->val = y;
    HASH_ADD_INT(idx_map, key, rec);
}

int queryHashTable(int x) {
    hashTable* rec;
    HASH_FIND_INT(idx_map, &x, rec);
    return rec->val;
}

struct TreeNode* helper(int in_left, int in_right, int* inorder, int* postorder) {
    // 如果这里没有节点构造二叉树了，就结束
    if (in_left > in_right) {
        return NULL;
    }

    // 选择 post_idx 位置的元素作为当前子树根节点
    int root_val = postorder[post_idx];
    struct TreeNode* root = malloc(sizeof(struct TreeNode));
    root->val = root_val;

    // 根据 root 所在位置分成左右两棵子树
    int index = queryHashTable(root_val);

    // 下标减一
    post_idx--;
    // 构造右子树
    root->right = helper(index + 1, in_right, inorder, postorder);
    // 构造左子树
    root->left = helper(in_left, index - 1, inorder, postorder);
    return root;
}

struct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize) {
    // 从后序遍历的最后一个元素开始
    post_idx = postorderSize - 1;

    // 建立（元素，下标）键值对的哈希表
    idx_map = NULL;
    int idx = 0;
    for (int i = 0; i < inorderSize; i++) {
        insertHashTable(inorder[i], idx++);
    }

    return helper(0, inorderSize - 1, inorder, postorder);
}

四.总结:

核心技巧：

（1）后序确定根，中序分左右

（2）使用哈希表加速查找