该学习笔记是观看下列视频所作,猛推,笔记有什么不对还请海涵指出https://www.bilibili.com/video/BV1M2UVBuEri?spm_id_from=333.788.videopod.episodes&vd_source=647b973f96e83d98bab38b26a3afe26c&p=2
从目的出发,为的是做什么呢,我输出一个东西,他能输出我想要的结果即可。则可以理解为,实际工作是为了预测下一次的输出结果,那怎么预测呢,是不是得寻找里输入和输出之间的关系,咋一看,这不就是函数吗,这也就回顾到人工智能最初的一个思想,符号主义,一切皆可用函数来实现。现在的问题就转化为,如何寻找一个这样准确的函数,可以精准的反馈这里的转化关系
向量化(Embedding)
在讨论函数之前,先提及函数数据处理转化过程,首先,我们先明确一个目标,大白话来讲,就是为了讲不同数据包括他所代表的含义转化统一性,标准的可计算数据。那么向量化具体是什么呢?
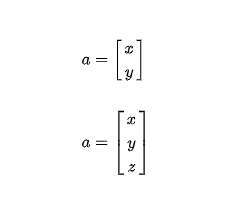
那向量长什么样子呢,如图,下面的就是对向量的矩阵化表达式
弄清了向量是什么样子之后,那这个东西是怎么处理成出来?以文字为案例,"我" -> 向量 ??? 有一个很简单粗暴的方式,直接一个数字代表一个文字,例如: 我:123 ,是:456,你:789..
但是,弊端也随之出现,文字和向量之间没有具体的关联性,单一维度不能表达过多的含义。维度不够那就加维度,使用Word2Vec可以将输入的文本转化成具体的向量,具体可以先查看这块相关视频了解一下。
函数 -> 神经网络

从一个简单的例子入手,我们所要寻找的函数就是如同上述图片的一类同属,输入a和m,经过牛顿第二定律转化,得到结果F。等比,输入一张图片,比如一张狗的图片,经过函数,得到结果,这个是狗的图片。这两个例子思想上是相似的。那,函数里面的具体怎么得出来呢?
如果给你下面这样一组数据,让你求出里面的函数关系:f(x) = y
x:[1,2,3,4,5]
y:[1,2,3,4,5]
是的,肉眼可以直观看出,这就是一条直接经过原点的直线 y = x,当然,也可以通过绘制xy坐标轴来求解答案,同理,我们最初的一个问题,也可以利用这个思想去解决。y = x ----> y = 1 * x + b
这样就可以收缩成一个线性问题,从原本的求解f(x) = y的f() 转化为求线性方程的y = xw + b 中的w 和 b ,给你一组数据,调节w和b可以快速定位到符合规律的方程。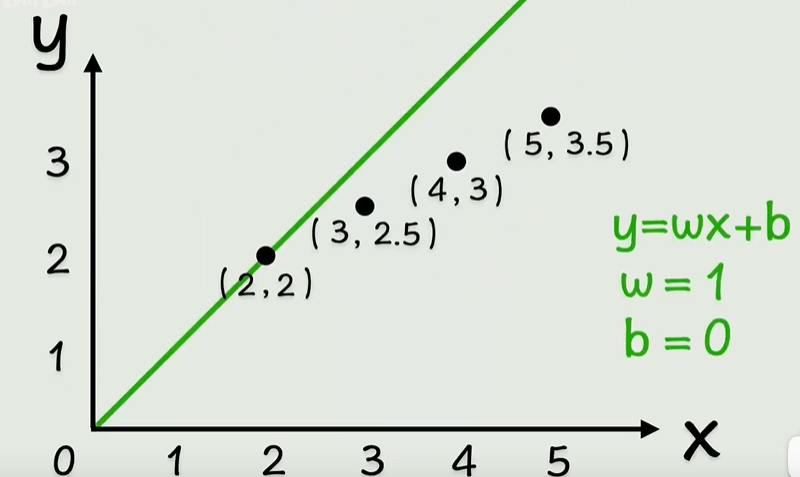
但是,数据分布并不是这么好呢,如同下面这个,怎么都涵盖不到具体的数据!!!!
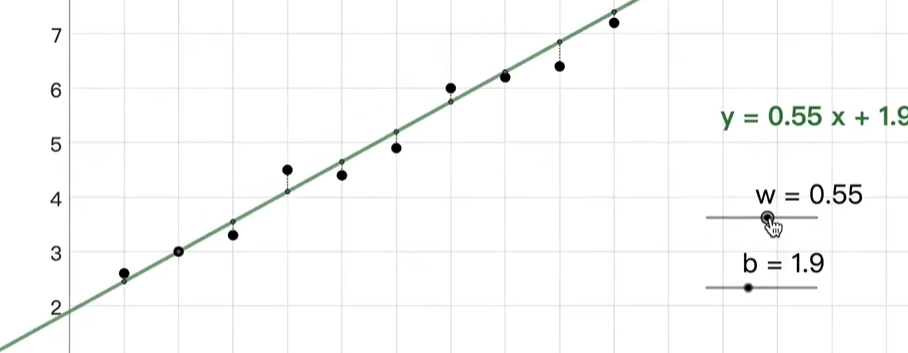
既然做不到完全精致,那就妥协吧,数据差不多在周边就行了,
这也就是人工智能从符号主义 -> 联结主义
继续回到寻找函数的问题,普通的线性函数实际上是很难满足到复杂的数据分布,例如下面的图表
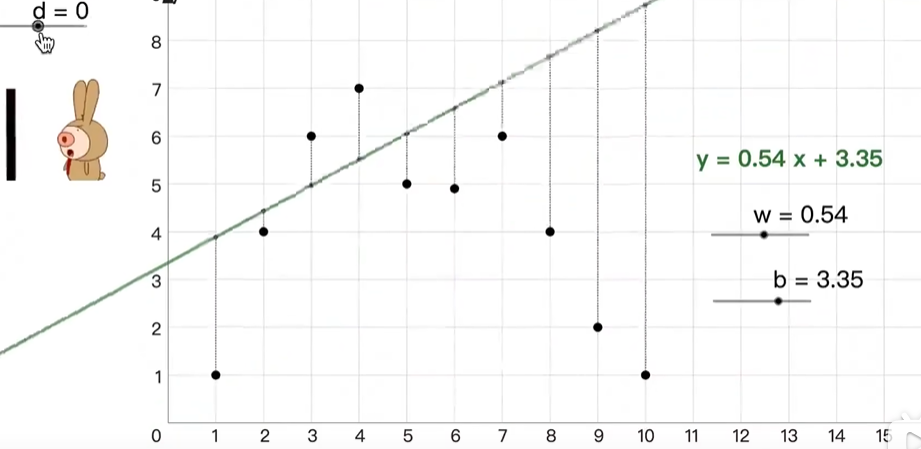
这就得将原本的线性方程转成为非线性方程,例如sin,cos, e,平方等等....这种在原本的线性函数上再套一层函数,这一层函数称激活函数g() =====> f(x) = g(wx + b) 。 有了激活函数,理论上,可以涵盖到如何一个数据关系,一个激活不行,就再套一个激活函数,无线套娃,一直写下去
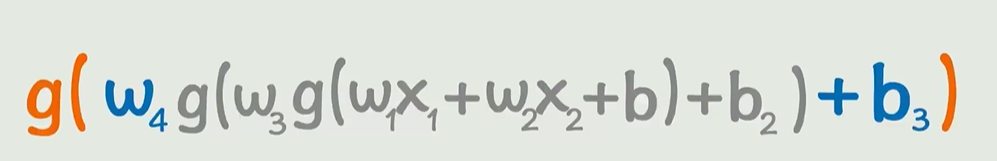
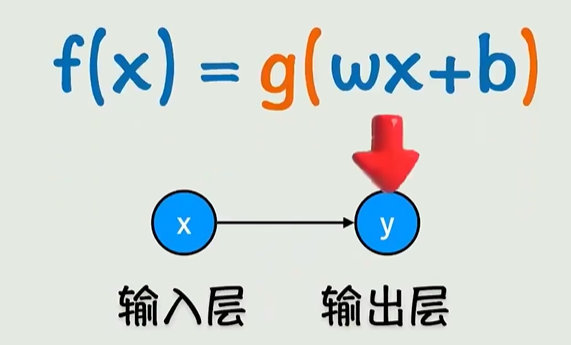
但是一直这么写,还挺麻烦,所以,可以统称为f(x):输入层, g(wx+b) 为输出层,这样可以描述为一个神经元(不等同现实神经元)
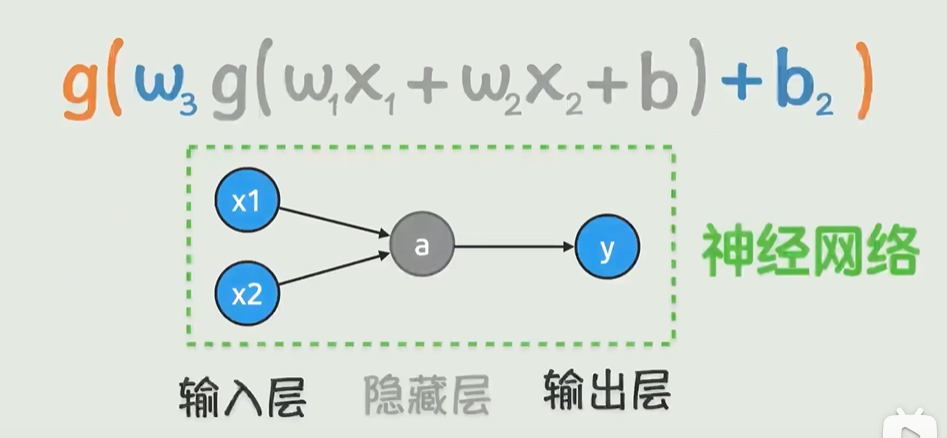
从上图来看,输入变量只有一个,输出转化也只有一层,套娃的机制不会停止,一个个神经元也就是构成了神经网络,理论上,每一层都可以无线添加。
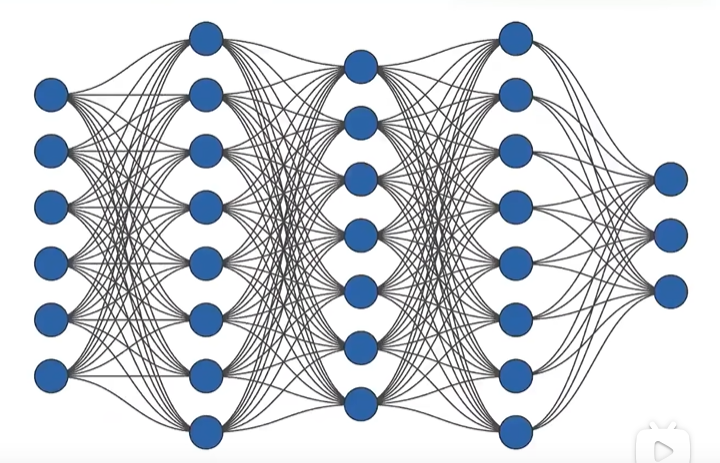
上述便是函数和神经网络之间的关系
还在写。。。。