周志华《机器学习—西瓜书》四

周志华《机器学习---西瓜书》四

四、决策树

4-1、决策树基本流程

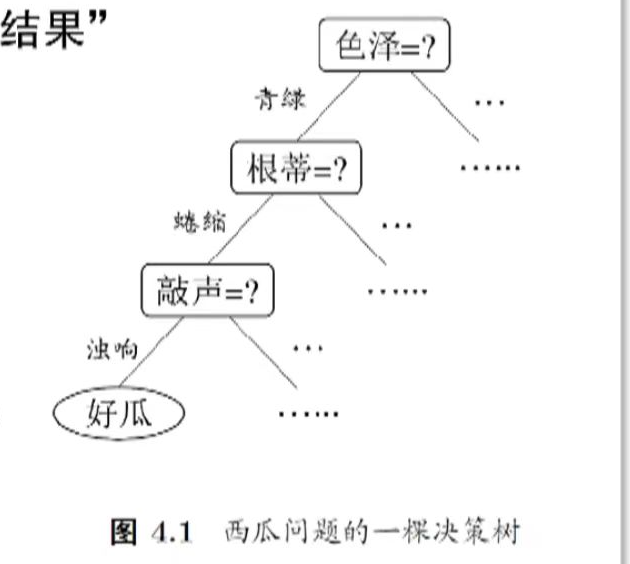
决策树基于"树"结构进行决策

每个"内部结点"对应于某个属性上的"测试"(test)
每个分支对应于该测试的一种可能结果（即该属性的某个取值）
每个"叶结点"对应于一个"预测结果"

学习过程

通过对训练样本的分析来确定"划分属性"（即内部结点所对应的属性）

预测过程

将测试示例从根结点开始，沿着划分属性所构成的"判定测试序列"下行，直到叶结点

策略： " 分而治之 " (divide-and-conquer)

自根至叶的递归过程，在每个中间结点寻找一个"划分"(split or test)属性

三种停止条件：

当前结点包含的样本全属于同一类别，无需划分；
当前属性集为空，或是所有样本在所有属性上取值相同，无法划分；
当前结点包含的样本集合为空，不能划分

基本算法

说明：

步骤 2-4 为递归返回情形 (1) ：样本全属于同一类别，直接标记为叶结点。
步骤 5-7 为递归返回情形 (2) ：无属性可分或样本在剩余属性上取值相同，标记为叶结点（类别取样本数最多的类）。
步骤 11-14 为递归返回情形 (3) ：若某分支无样本，标记为叶结点（类别取父结点样本最多的类）。
步骤 8 是决策树算法的核心：选择最优划分属性，决定了树的生长质量。

‍

4-2、信息增益(Information Gain)

信息熵 (entropy) 是度量样本集合"纯度"最常用的一种指标。
假定当前样本集合 ( D ) ( D ) (D) 中第 ( k ) ( k ) (k) 类样本所占的比例为 ( p k ) ( p_k ) (pk)，则 ( D ) 的信息熵定义为：

Ent ( D ) = − ∑ k = 1 ∣ Y ∣ p k log ⁡ 2 p k \text{Ent}(D) = -\sum_{k=1}^{|\mathcal{Y}|} p_k \log_2 p_k Ent(D)=−k=1∑∣Y∣pklog2pk
- 计算信息熵时必须约定：若 ( p = 0 ) ( p = 0 ) (p=0)，则 ( p log ⁡ 2 p = 0 ) ( p\log_2 p = 0 ) (plog2p=0)。
- ( Ent ( D ) ) ( \text{Ent}(D) ) (Ent(D))的最小值为 0 0 0，最大值为 log ⁡ 2 ∣ Y ∣ \log_2 |\mathcal{Y}| log2∣Y∣。
- ( Ent ( D ) ) ( \text{Ent}(D) ) (Ent(D)) 的值越小，则 D D D 的纯度越高。
信息增益直接以信息熵为基础，计算当前划分对信息熵所造成的变化。
离散属性 a 的取值： { a 1 , a 2 , ... , a V } \{a^1, a^2, \dots, a^V\} {a1,a2,...,aV}
D v D^v Dv ：D 中在 a 上取值 = a v = a^v =av 的样本集合
以属性 a 对数据集 D 进行划分所获得的信息增益为：

Gain ( D , a ) = Ent ( D ) ⏟ 划分前的信息熵 − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ ⏟ 第 v 个分支的权重，样本越多越重要 Ent ( D v ) ⏟ 划分后的信息熵 \text{Gain}(D, a) = \underbrace{\text{Ent}(D)}{\text{划分前的信息熵}} - \sum{v=1}^{V} \underbrace{\frac{|D^v|}{|D|}}{\text{第 } v \text{ 个分支的权重，样本越多越重要}} \underbrace{\text{Ent}(D^v)}{\text{划分后的信息熵}} Gain(D,a)=划分前的信息熵 Ent(D)−v=1∑V第 v 个分支的权重，样本越多越重要 ∣D∣∣Dv∣划分后的信息熵 Ent(Dv)
该方法在 " ID3算法 "中使用

举例：

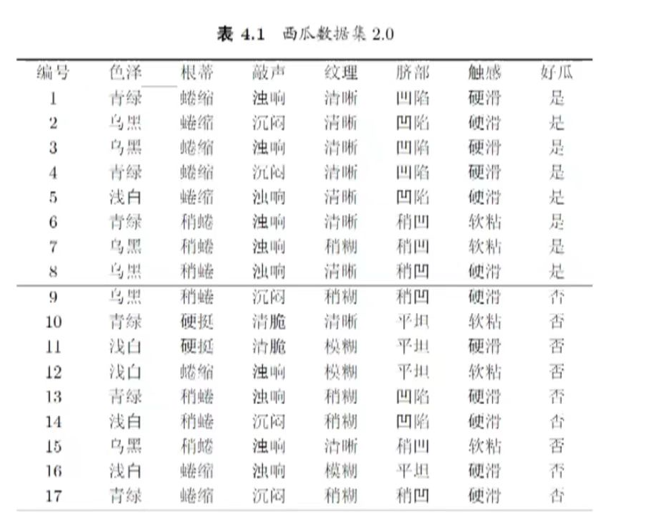
步骤1：计算根结点的信息熵

已知数据集 ( D ) 包含17个样本，正例（好瓜=是）有8个，反例（好瓜=否）有9个。

根据信息熵公式：

Ent ( D ) = − ∑ k = 1 2 p k log ⁡ 2 p k \text{Ent}(D) = -\sum_{k=1}^{2} p_k \log_2 p_k Ent(D)=−k=1∑2pklog2pk

其中 ( p 1 = 8 17 ) ， ( p 2 = 9 17 ) ( p_1 = \frac{8}{17} )，( p_2 = \frac{9}{17} ) (p1=178)，(p2=179)，代入得：

Ent ( D ) = − ( 8 17 log ⁡ 2 8 17 + 9 17 log ⁡ 2 9 17 ) ≈ 0.998 \text{Ent}(D) = -\left( \frac{8}{17} \log_2 \frac{8}{17} + \frac{9}{17} \log_2 \frac{9}{17} \right) \approx 0.998 Ent(D)=−(178log2178+179log2179)≈0.998

步骤2：计算属性"色泽"的信息增益

"色泽"有3个取值：青绿、乌黑、浅白，对应子集 D 1 , D 2 , D 3 D^1, D^2, D^3 D1,D2,D3

子集 ( D^1 )（色泽=青绿） ：共6个样本，正例3个，反例3个。

信息熵：

Ent ( D 1 ) = − ( 3 6 log ⁡ 2 3 6 + 3 6 log ⁡ 2 3 6 ) = 1.000 \text{Ent}(D^1) = -\left( \frac{3}{6} \log_2 \frac{3}{6} + \frac{3}{6} \log_2 \frac{3}{6} \right) = 1.000 Ent(D1)=−(63log263+63log263)=1.000
子集 ( D^2 )（色泽=乌黑） ：共6个样本，正例4个，反例2个。

信息熵：

Ent ( D 2 ) = − ( 4 6 log ⁡ 2 4 6 + 2 6 log ⁡ 2 2 6 ) ≈ 0.918 \text{Ent}(D^2) = -\left( \frac{4}{6} \log_2 \frac{4}{6} + \frac{2}{6} \log_2 \frac{2}{6} \right) \approx 0.918 Ent(D2)=−(64log264+62log262)≈0.918
子集 ( D^3 )（色泽=浅白） ：共5个样本，正例1个，反例4个。

信息熵：

Ent ( D 3 ) = − ( 1 5 log ⁡ 2 1 5 + 4 5 log ⁡ 2 4 5 ) ≈ 0.722 \text{Ent}(D^3) = -\left( \frac{1}{5} \log_2 \frac{1}{5} + \frac{4}{5} \log_2 \frac{4}{5} \right) \approx 0.722 Ent(D3)=−(51log251+54log254)≈0.722

根据信息增益公式：

Gain ( D , 色泽 ) = Ent ( D ) − ∑ v = 1 3 ∣ D v ∣ ∣ D ∣ Ent ( D v ) ] 代入 ( ∣ D 1 ∣ = 6 ) ， ( ∣ D 2 ∣ = 6 ) ， ( ∣ D 3 ∣ = 5 ) ， ( ∣ D ∣ = 17 ) \text{Gain}(D, \text{色泽}) = \text{Ent}(D) - \sum_{v=1}{3} \frac{|Dv|}{|D|} \text{Ent}(Dv)]代入 ( |D1|=6 )，( |D^2|=6 )，( |D^3|=5 )，( |D|=17 ) Gain(D,色泽)=Ent(D)−v=1∑3∣D∣∣Dv∣Ent(Dv)]代入(∣D1∣=6)，(∣D2∣=6)，(∣D3∣=5)，(∣D∣=17)

得：

Gain ( D , 色泽 ) = 0.998 − ( 6 17 × 1.000 + 6 17 × 0.918 + 5 17 × 0.722 ) ≈ 0.109 \text{Gain}(D, \text{色泽}) = 0.998 - \left( \frac{6}{17} \times 1.000 + \frac{6}{17} \times 0.918 + \frac{5}{17} \times 0.722 \right) \approx 0.109 Gain(D,色泽)=0.998−(176×1.000+176×0.918+175×0.722)≈0.109

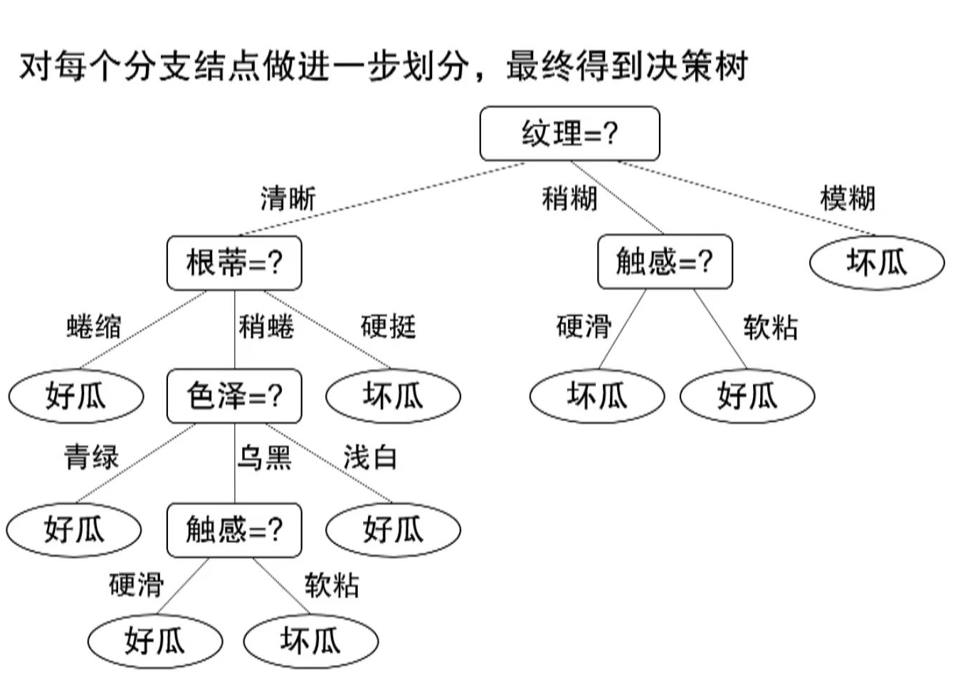
步骤3：计算其他属性的信息增益（以"纹理"为例，最终选择信息增益最大的属性）

类似地，计算"根蒂""敲声""纹理""脐部""触感"的信息增益：

( Gain ( D , 根蒂 ) ≈ 0.143 ) ( \text{Gain}(D, \text{根蒂}) \approx 0.143 ) (Gain(D,根蒂)≈0.143)
( Gain ( D , 敲声 ) ≈ 0.141 ) ( \text{Gain}(D, \text{敲声}) \approx 0.141 ) (Gain(D,敲声)≈0.141)
( Gain ( D , 纹理 ) ≈ 0.381 ) ( \text{Gain}(D, \text{纹理}) \approx 0.381 ) (Gain(D,纹理)≈0.381)（最大，选为划分属性）
( Gain ( D , 脐部 ) ≈ 0.289 ) ( \text{Gain}(D, \text{脐部}) \approx 0.289 ) (Gain(D,脐部)≈0.289)
( Gain ( D , 触感 ) ≈ 0.006 ) ( \text{Gain}(D, \text{触感}) \approx 0.006 ) (Gain(D,触感)≈0.006)

综上，通过计算各属性的信息增益，选择"纹理"作为最优划分属性，后续可继续对其子集递归划分。

‍

4-3、其他属性划分准则

增益率 (Gain Ratio)

信息增益对可取值数目较多的属性存在偏好，有明显的弱点（例如"编号"这类属性会因取值过多而获得高信息增益，但无实际分类意义）。

增益率是为解决这一问题提出的指标，用于C4.5算法中选择最优划分属性。

公式与解释

增益率公式：

Gain_ratio ( D , a ) = Gain ( D , a ) IV ( a ) \text{Gain\_ratio}(D, a) = \frac{\text{Gain}(D, a)}{\text{IV}(a)} Gain_ratio(D,a)=IV(a)Gain(D,a)
其中， IV ( a ) \text{IV}(a) IV(a) 是属性 a a a 的固有值 (Intrinsic Value) ，计算公式为：

IV ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ log ⁡ 2 ∣ D v ∣ ∣ D ∣ \text{IV}(a) = -\sum_{v=1}^{V} \frac{|D^v|}{|D|} \log_2 \frac{|D^v|}{|D|} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣

固有值的特点：属性 a a a 的可能取值数目越多（即 V V V 越大）， IV ( a ) \text{IV}(a) IV(a) 通常越大，从而抵消多取值属性在信息增益上的"优势"。

选择策略

采用**++启发式方法++**：先从候选划分属性中找出信息增益高于平均水平的，再从中选取增益率最高的属性。

‍

基尼指数 (Gini Index)

基尼指数用于度量数据集的"纯度"，公式为：

Gini ( D ) = ∑ k = 1 ∣ Y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ Y ∣ p k 2 \begin{align*} \text{Gini}(D) &= \sum_{k=1}^{|\mathcal{Y}|} \sum_{k'\neq k} p_k p_{k'} \\ &= 1 - \sum_{k=1}^{|\mathcal{Y}|} p_k^2 \end{align*} Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=1−k=1∑∣Y∣pk2

其物理意义是：从数据集 ( D ) 中随机抽取两个样例，类别标记不一致的概率。
性质： Gini ( D ) \text{Gini}(D) Gini(D) 越小，数据集 D D D 的纯度越高。

属性的基尼指数

对于属性 ( a )，其基尼指数计算公式为：

Gini_index ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Gini ( D v ) \text{Gini\index}(D, a) = \sum{v=1}^{V} \frac{|D^v|}{|D|} \text{Gini}(D^v) Gini_index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)

中 D v D^v Dv 是数据集 D 中属性 a 取值为 a v a^v av 的样本子集。

应用与选择策略

在候选属性集合中，选取使划分后基尼指数 最小****的属性，该方法用于CART算法中。

‍

4-4、划分和剪枝

研究表明：划分选择的各种准则虽然对决策树的尺寸有较大影响，但对泛化性能的影响很有限

例如信息增益与基尼指数产生的结果，仅在约2%的情况下不同

剪枝方法和程度对决策树泛化性能的影响更为显著

在数据带噪时甚至可能将泛化性能提升25%

Why? 剪枝 (pruning) 是决策树对付" 过拟合 " 的主要手段！

剪枝：

为了尽可能正确分类训练样本，有可能造成分支过多 ------> 过拟合

可通过主动去掉一些分支来降低过拟合的风险

基本策略：

预剪枝(pre-pruning):提前终止某些分支的生长
后剪枝（post-pruning):生成一棵完全树，再"回头"剪枝

剪枝过程中需评估剪枝前后决策树的优劣 -------> 第二章模型性能评估

4-5、缺失值的处理

缺失值：

现实应用中经常遇到属性值 "缺失"(missing) 的现象。如果仅使用无缺失的样例 ------------> 会造成对数据的极大浪费。
使用带缺失值的样例时，需解决两个问题:
- Q1：如何进行划分属性选择？
- Q2：给定划分属性，若样本在该属性上的值缺失，如何进行划分？
基本思路：样本赋权，权重划分
举例：

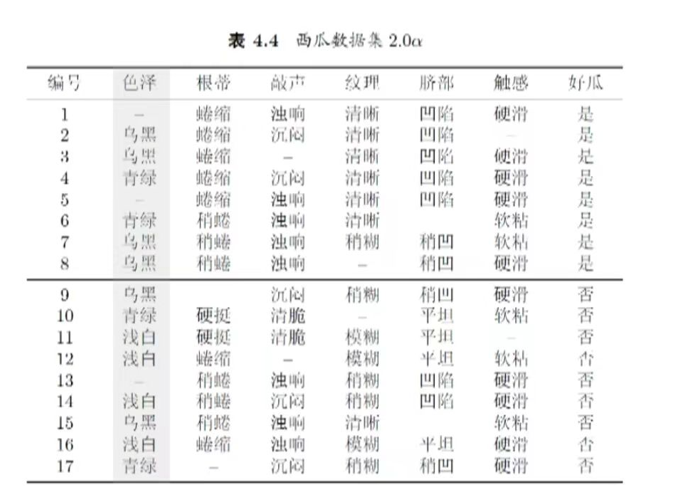
仅通过无缺失值的样例来判断划分属性的优劣

这例子，展示了含缺失值时决策树划分属性选择（信息增益计算） 和缺失值样本划分（权重划分） 的过程，具体计算内容如下：

一、划分属性选择：信息增益计算

以"色泽"属性为例，步骤如下：
1. 计算无缺失值子集 ** D ~ \tilde{D} D~ 的信息熵**
  
  无缺失值的样例数为14，其中"好瓜=是"有6个，"好瓜=否"有8个。
  
  信息熵公式： Ent ( D ~ ) = − ∑ k = 1 2 p ~ k log ⁡ 2 p ~ k \text{Ent}(\tilde{D}) = -\sum_{k=1}^{2} \tilde{p}_k \log_2 \tilde{p}_k Ent(D~)=−∑k=12p~klog2p~k
  
  代入计算：
  Ent ( D ~ ) = − ( 6 14 log ⁡ 2 6 14 + 8 14 log ⁡ 2 8 14 ) ≈ 0.985 \text{Ent}(\tilde{D}) = -\left( \frac{6}{14}\log_2\frac{6}{14} + \frac{8}{14}\log_2\frac{8}{14} \right) \approx 0.985 Ent(D~)=−(146log2146+148log2148)≈0.985
2. 计算各取值分支的信息熵
  
  令 D ~ 1 \tilde{D}^1 D~1（青绿）、 D ~ 2 \tilde{D}^2 D~2（乌黑）、 D ~ 3 \tilde{D}^3 D~3（浅白）为"色泽"取值的子集：
  - D ~ 1 \tilde{D}^1 D~1（4个样例，2是2否）： Ent ( D ~ 1 ) = − ( 2 4 log ⁡ 2 2 4 + 2 4 log ⁡ 2 2 4 ) = 1.000 \text{Ent}(\tilde{D}^1) = -\left( \frac{2}{4}\log_2\frac{2}{4} + \frac{2}{4}\log_2\frac{2}{4} \right) = 1.000 Ent(D~1)=−(42log242+42log242)=1.000
  - D ~ 2 \tilde{D}^2 D~2（6个样例，4是2否）： Ent ( D ~ 2 ) = − ( 4 6 log ⁡ 2 4 6 + 2 6 log ⁡ 2 2 6 ) ≈ 0.918 \text{Ent}(\tilde{D}^2) = -\left( \frac{4}{6}\log_2\frac{4}{6} + \frac{2}{6}\log_2\frac{2}{6} \right) \approx 0.918 Ent(D~2)=−(64log264+62log262)≈0.918
  - D ~ 3 \tilde{D}^3 D~3（4个样例，0是4否）： Ent ( D ~ 3 ) = − ( 0 4 log ⁡ 2 0 4 + 4 4 log ⁡ 2 4 4 ) = 0.000 \text{Ent}(\tilde{D}^3) = -\left( \frac{0}{4}\log_2\frac{0}{4} + \frac{4}{4}\log_2\frac{4}{4} \right) = 0.000 Ent(D~3)=−(40log240+44log244)=0.000
3. 计算 ** D ~ \tilde{D} D~ 上"色泽"的信息增益**
  
  信息增益公式： Gain ( D ~ , 色泽 ) = Ent ( D ~ ) − ∑ v = 1 3 r ~ v Ent ( D ~ v ) \text{Gain}(\tilde{D}, \text{色泽}) = \text{Ent}(\tilde{D}) - \sum_{v=1}^{3} \tilde{r}_v \text{Ent}(\tilde{D}^v) Gain(D~,色泽)=Ent(D~)−∑v=13r~vEnt(D~v)
  
  其中 r ~ v \tilde{r}_v r~v是无缺失值样例中属性取 v v v的占比（ r ~ 1 = 4 14 , r ~ 2 = 6 14 , r ~ 3 = 4 14 \tilde{r}_1=\frac{4}{14}, \tilde{r}_2=\frac{6}{14}, \tilde{r}_3=\frac{4}{14} r~1=144,r~2=146,r~3=144）。
  
  代入计算：
  Gain ( D ~ , 色泽 ) = 0.985 − ( 4 14 × 1.000 + 6 14 × 0.918 + 4 14 × 0.000 ) ≈ 0.306 \text{Gain}(\tilde{D}, \text{色泽}) = 0.985 - \left( \frac{4}{14} \times 1.000 + \frac{6}{14} \times 0.918 + \frac{4}{14} \times 0.000 \right) \approx 0.306 Gain(D~,色泽)=0.985−(144×1.000+146×0.918+144×0.000)≈0.306
4. 计算整个样本集 ** D D D 上"色泽"的信息增益**
  
  公式： Gain ( D , 色泽 ) = ρ × Gain ( D ~ , 色泽 ) \text{Gain}(D, \text{色泽}) = \rho \times \text{Gain}(\tilde{D}, \text{色泽}) Gain(D,色泽)=ρ×Gain(D~,色泽)
  
  其中 ρ \rho ρ是无缺失值样例占比（ ρ = 14 17 \rho = \frac{14}{17} ρ=1714）。
  
  代入计算：
  Gain ( D , 色泽 ) = 14 17 × 0.306 ≈ 0.252 \text{Gain}(D, \text{色泽}) = \frac{14}{17} \times 0.306 \approx 0.252 Gain(D,色泽)=1714×0.306≈0.252
二、所有属性的信息增益对比

类似计算其他属性后，得到：
- Gain ( D , 色泽 ) = 0.252 \text{Gain}(D, \text{色泽}) = 0.252 Gain(D,色泽)=0.252
- Gain ( D , 根蒂 ) = 0.171 \text{Gain}(D, \text{根蒂}) = 0.171 Gain(D,根蒂)=0.171
- Gain ( D , 敲声 ) = 0.145 \text{Gain}(D, \text{敲声}) = 0.145 Gain(D,敲声)=0.145
- Gain ( D , 纹理 ) = 0.424 \text{Gain}(D, \text{纹理}) = 0.424 Gain(D,纹理)=0.424（最大，因此选"纹理"作为划分属性）
- Gain ( D , 脐部 ) = 0.289 \text{Gain}(D, \text{脐部}) = 0.289 Gain(D,脐部)=0.289
- Gain ( D , 触感 ) = 0.006 \text{Gain}(D, \text{触感}) = 0.006 Gain(D,触感)=0.006
三、缺失值样本的划分：权重划分

以"纹理"属性（信息增益最大）为例，对缺失值样本（如样本8、10）的处理：
- 样本8、10在"纹理"上缺失，需按权重划分到所有分支。
- 权重分配：根据"纹理=清晰""稍糊""模糊"的样本占比，分别为 7 15 \frac{7}{15} 157、 5 15 \frac{5}{15} 155、 3 15 \frac{3}{15} 153，即样本8、10同时进入三个分支，权重按此比例分配。

‍