周志华《机器学习---西瓜书》三

三、线性回归

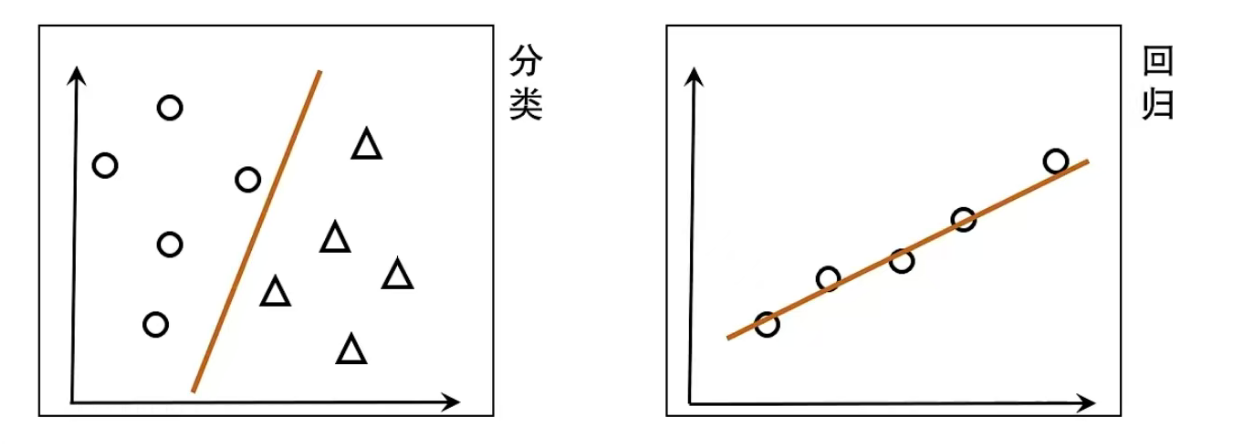
3-1、基本线性回归：

线性模型试图学的一个通过属性的线性组合来进行预测的函数式为 f(x)=w1x1+w2x2+⋯+wdxd+bf(\boldsymbol{x}) = w_1x_1 + w_2x_2 + \dots + w_dx_d + bf(x)=w1x1+w2x2+⋯+wdxd+b

向量形式：f(x)=wTx+bf(\boldsymbol{x}) = \boldsymbol{w}^\text{T}\boldsymbol{x} + bf(x)=wTx+b 其中 w=(w1,w2,...,wd)T\boldsymbol{w} = (w_1, w_2, \dots, w_d)^\text{T}w=(w1,w2,...,wd)T 是权重向量，bbb 是偏置

优点：简单、基本、可理解性好

可以分为：离散变量和连续变量

目标： f(xi)=wxi+bf(x_i) = wx_i + bf(xi)=wxi+b 目标是让 f(xi)≈yif(x_i) \approx y_if(xi)≈yi

离散属性的处理：若有 " 序 " （order），则连续化；否则，转化为k维向量

最小二乘法求解过程：

令均方误差最小化有：

(w∗,b∗)=arg⁡min⁡(w,b)∑i=1m(f(xi)−yi)2=arg⁡min⁡(w,b)∑i=1m(yi−wxi−b)2 \begin{align*} (w^*, b^*) &= \arg\min_{(w,b)} \sum_{i=1}^m \left(f\left(x_i\right) - y_i\right)^2 \\ &= \arg\min_{(w,b)} \sum_{i=1}^m \left(y_i - wx_i - b\right)^2 \end{align*} (w∗,b∗)=arg(w,b)mini=1∑m(f(xi)−yi)2=arg(w,b)mini=1∑m(yi−wxi−b)2

然后对 E(w,b)=∑i=1m(yi−wxi−b)2E_{(w,b)} = \sum_{i=1}^m (y_i - wx_i - b)^2E(w,b)=∑i=1m(yi−wxi−b)2 进行最小二乘参数估计。其中m 是样本数量

损失函数： E(w,b)=∑i=1m(yi−wxi−b)2E_{(w,b)} = \sum_{i=1}^m (y_i - wx_i - b)^2E(w,b)=∑i=1m(yi−wxi−b)2

对www求偏导： ∂E(w,b)∂w=2(w∑i=1mxi2−∑i=1m(yi−b)xi)\frac{\partial E_{(w,b)}}{\partial w} = 2\left( w\sum_{i=1}^{m} x_i^2 - \sum_{i=1}^{m} (y_i - b)x_i \right)∂w∂E(w,b)=2(w∑i=1mxi2−∑i=1m(yi−b)xi)

对bbb求偏导： ∂E(w,b)∂b=2(mb−∑i=1m(yi−wxi))\frac{\partial E_{(w,b)}}{\partial b} = 2\left( mb - \sum_{i=1}^{m} (y_i - wx_i) \right)∂b∂E(w,b)=2(mb−∑i=1m(yi−wxi))

闭式解（令导数为0求解）：

权重( w )： w=∑i=1myi(xi−xˉ)∑i=1mxi2−1m(∑i=1mxi)2w = \frac{\sum_{i=1}^{m} y_i (x_i - \bar{x})}{\sum_{i=1}^{m} x_i^2 - \frac{1}{m}\left( \sum_{i=1}^{m} x_i \right)^2}w=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−xˉ)

偏置( b )： b=1m∑i=1m(yi−wxi)b = \frac{1}{m}\sum_{i=1}^{m} (y_i - wx_i)b=m1∑i=1m(yi−wxi)

3-2、多元线性回归

模型： f(xi)=wTxi+b使得f(xi)≃yif \left( \boxed{x}_i \right) = \boxed{w}^\mathrm{T} \boxed{x}_i + b \quad \text{使得} \quad f \left( \boxed{x}_i \right) \simeq y_if(xi)=wTxi+b使得f(xi)≃yi

变量定义：样本特征向量：xi=(xi1;xi2;... ;xid)\boxed{x}i = (x{i1}; x_{i2}; \dots; x_{id})xi=(xi1;xi2;...;xid)

样本标签：yi∈Ry_i \in \mathbb{R}yi∈R

向量形式与数据集表示：

将权重 w\boxed{w}w 和偏置 bbb 吸收为向量w^=(w;b)\hat{\boxed{w}} = (\boxed{w}; b)w^=(w;b) ，数据集表示为：

特征矩阵 X\mathbf{X}X：
X=(x11x12⋯x1d1x21x22⋯x2d1⋮⋮⋱⋮⋮xm1xm2⋯xmd1)=(x1T1x2T1⋮⋮xmT1)\mathbf{X} = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{md} & 1 \\ \end{pmatrix} = \begin{pmatrix} \boxed{x}_1^\mathrm{T} & 1 \\ \boxed{x}_2^\mathrm{T} & 1 \\ \vdots & \vdots \\ \boxed{x}_m^\mathrm{T} & 1 \\ \end{pmatrix}X= x11x21⋮xm1x12x22⋮xm2⋯⋯⋱⋯x1dx2d⋮xmd11⋮1 = x1Tx2T⋮xmT11⋮1
标签向量 y\boxed{y}y ：

y=(y1;y2;... ;ym)\boxed{y} = (y_1; y_2; \dots; y_m)y=(y1;y2;...;ym)

同样采用最小二乘法求解：

多元线性回归的最小二乘求解

优化目标： w^∗=arg⁡min⁡w^(y−Xw^)T(y−Xw^)\hat{w}^* = \arg\min_{\hat{w}} \left( y - \mathbf{X}\hat{w} \right)^\mathrm{T} \left( y - \mathbf{X}\hat{w} \right)w^∗=argminw^(y−Xw^)T(y−Xw^)

损失函数定义： Ew^=(y−Xw^)T(y−Xw^)E_{\hat{w}} = \left( y - \mathbf{X}\hat{w} \right)^\mathrm{T} \left( y - \mathbf{X}\hat{w} \right)Ew^=(y−Xw^)T(y−Xw^)

对 w^\hat{w}w^求偏导： ∂Ew^∂w^=2XT(Xw^−y)\frac{\partial E_{\hat{w}}}{\partial \hat{w}} = 2\mathbf{X}^\mathrm{T} \left( \mathbf{X}\hat{w} - y \right)∂w^∂Ew^=2XT(Xw^−y)

令偏导为 0，求解 w^\hat{w}w^ ，闭式解（矩阵满秩 / 正定情况）： w^∗=(XTX)−1XTy\hat{w}^* = \left( \mathbf{X}^\mathrm{T}\mathbf{X} \right)^{-1} \mathbf{X}^\mathrm{T}yw^∗=(XTX)−1XTy

说明：若 XTX\mathbf{X}^\mathrm{T}\mathbf{X}XTX 不满秩，会存在多个解，此时需引入正则化

3-3、线性模型变化

令预测值逼近y的衍生物?

对于样例 (x,y)（y∈R）(x, y) （y \in \mathbb{R}）(x,y)（y∈R），希望线性模型的预测值逼近真实标记，得到线性回归模型 y=wTx+by = w^\mathrm{T}x + by=wTx+b

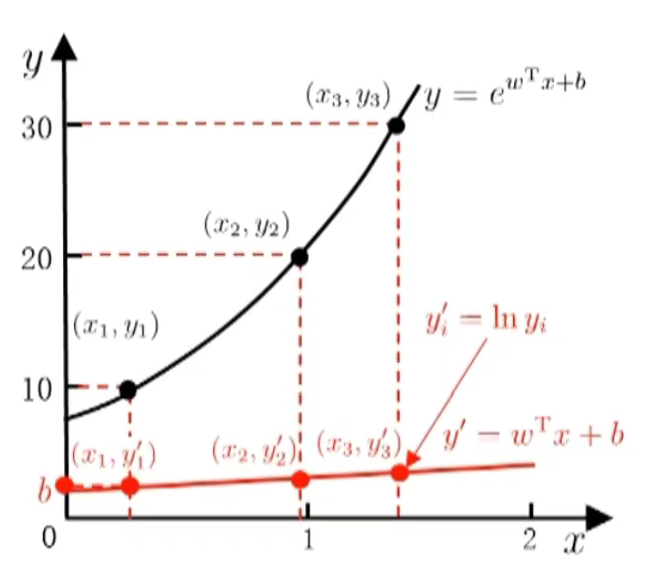
若令预测值逼近 y 的衍生物 ，例如令：ln⁡y=wTx+b\ln y = w^\mathrm{T}x + blny=wTx+b 则得到对数线性回归（log-linear regression） 。

其本质是用 ewTx+be^{w^\mathrm{T}x + b}ewTx+b 逼近 y，即模型实际形式为： y≈ewTx+by \approx e^{w^\mathrm{T}x + b}y≈ewTx+b

右侧图表直观展示了这一过程：对原始标签 yiy_iyi 取对数 yi′=ln⁡yiy_i' = \ln y_iyi′=lnyi 后， y′y'y′ 与线性模型 wTx+bw^\mathrm{T}x + bwTx+b 拟合，而原始 y 则由指数形式 ewTx+be^{w^\mathrm{T}x + b}ewTx+b 逼近。

‍

3-4、广义线性模型

一般形式： y=g−1(wTx+b)y = g^{-1} \left( w^\mathrm{T}x + b \right)y=g−1(wTx+b)

其中，(g−1)( g^{-1} )(g−1)是 单调可微的联系函数（link function） 。

示例（对数线性回归）：

令 (g(⋅)=ln⁡(⋅))( g(\cdot) = \ln(\cdot) )(g(⋅)=ln(⋅)) ，则模型形式为： ln⁡y=wTx+b\ln y = w^\mathrm{T}x + blny=wTx+b

‍

3-5、二分类任务

线性回归模型的实值输出：(z=wTx+b)( z = {w}^\mathrm{T}{x} + b )(z=wTx+b)
二分类的期望输出：y∈（0,1）y \in （{ 0, 1 } ）y∈（0,1）
核心问题：找 ( z ) 和 ( y ) 的联系函数

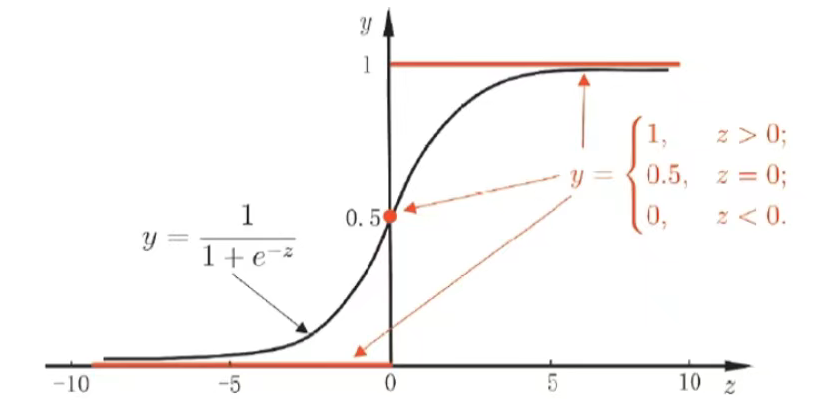
理想的"单位阶跃函数"（unit-step function）

y={0,z<0;0.5,z=0;1,z>0, y = \begin{cases} 0, & z < 0; \\ 0.5, & z = 0; \\ 1, & z > 0, \end{cases} y=⎩ ⎨ ⎧0,0.5,1,z<0;z=0;z>0,

该函数性质不好（不连续、不可微），需找替代函数 （surrogate function） 。

常用替代：对数几率函数（logistic function，简称"对率函数"）

y=11+e−zy = \frac{1}{1 + e^{-z}}y=1+e−z1

它具有单调可微、任意阶可导的性质，可作为单位阶跃函数的光滑近似。

注意事项

Logistic 与"逻辑"无直接关系：

其词源是 Logit，而非 Logic；
输出是实数值（概率意义），并非"非0即1"的逻辑值。

3-6、对率回归

以对率函数为联系函数，将 y=11+e−zy = \frac{1}{1 + e^{-z}}y=1+e−z1 中的 z 替换为 wTx+b{w}^\mathrm{T}{x} + bwTx+b，得到：

变形可得：
ln⁡(y1−y)=wTx+b\ln\left( \frac{y}{1 - y} \right) = \boxed{w}^\mathrm{T}\boxed{x} + bln(1−yy)=wTx+b

其中，y1−y\frac{y}{1 - y}1−yy 是几率（odds） ，反映了 ( x ) 作为正例的相对可能性； ln⁡(y1−y)\ln\left( \frac{y}{1 - y} \right)ln(1−yy) 是对数几率（log odds，亦称 logit） 。

该模型称为对数几率回归（logistic regression） ，简称对率回归。

对率回归的特点

无需事先假设数据分布；
可得到"类别"的近似概率预测；
可直接应用现有数值优化算法求取最优解

注意：它是分类学习算法！

求解思路

变量简化：令 β=(w;b)，x^=(x;1)\beta = (w; b)，\hat{x} = (x; 1)β=(w;b)，x^=(x;1)，则 wTx+bw^\mathrm{T}x + bwTx+b 可简写为 βTx^\beta^\mathrm{T}\hat{x}βTx^。
概率定义：
定义正例概率 : p1(x^i;β)=p(y=1∣x^;β)=ewTx+b1+ewTx+bp_1(\hat{x}_i; \beta) = p(y=1 \mid \hat{x}; \beta) = \frac{e^{w^\mathrm{T}x+b}}{1 + e^{w^\mathrm{T}x+b}}p1(x^i;β)=p(y=1∣x^;β)=1+ewTx+bewTx+b；
负例概率 p0(x^i;β)=p(y=0∣x^;β)=1−p1(x^i;β)=11+ewTx+bp_0(\hat{x}_i; \beta) = p(y=0 \mid \hat{x}; \beta) = 1 - p_1(\hat{x}_i; \beta) = \frac{1}{1 + e^{w^\mathrm{T}x+b}}p0(x^i;β)=p(y=0∣x^;β)=1−p1(x^i;β)=1+ewTx+b1。
似然项重写： p(yi∣xi;w,b)=yip1(x^i;β)+(1−yi)p0(x^i;β)p(y_i \mid x_i; w, b) = y_i p_1(\hat{x}_i; \beta) + (1 - y_i) p_0(\hat{x}_i; \beta)p(yi∣xi;w,b)=yip1(x^i;β)+(1−yi)p0(x^i;β)。
最大化似然函数：
似然函数 ℓ(w,b)=∑i=1mln⁡p(yi∣xi;w,b)\ell(w, b) = \sum_{i=1}^{m} \ln p(y_i \mid x_i; w, b)ℓ(w,b)=∑i=1mlnp(yi∣xi;w,b) ，
等价于最小化 ℓ(β)=∑i=1m(−yiβTx^i+ln⁡(1+eβTx^i))\ell(\beta) = \sum_{i=1}^{m} \left( -y_i \beta^\mathrm{T}\hat{x}_i + \ln\left( 1 + e^{\beta^\mathrm{T}\hat{x}_i} \right) \right)ℓ(β)=∑i=1m(−yiβTx^i+ln(1+eβTx^i))。
优化特性：
该目标函数是高阶可导的连续凸函数，可通过经典数值优化方法（如梯度下降法、牛顿法）求解。

手推：

最大化联合概率：
max⁡(P(真是+)P(预测为+)+P(真是−)P(预测为−))\max \left( P(\text{真是}+)P(\text{预测为}+) + P(\text{真是}-)P(\text{预测为}-) \right)max(P(真是+)P(预测为+)+P(真是−)P(预测为−))
取对数后（似然函数的对数形式）： max⁡（ln⁡(y⋅eβTx1+eβTx+(1−y)⋅11+eβTx)）\max （ \ln \left( y \cdot \frac{e^{\beta^\mathrm{T}x}}{1 + e^{\beta^\mathrm{T}x}} + (1 - y) \cdot \frac{1}{1 + e^{\beta^\mathrm{T}x}} \right) ）max（ln(y⋅1+eβTxeβTx+(1−y)⋅1+eβTx1)）

说明：其中，yyy 为真实标签 y=1y=1y=1 表示正例， y=0y=0y=0 表示负例）， βTx\beta^\mathrm{T}xβTx 是线性组合项，eβTx1+eβTx\frac{e^{\beta^\mathrm{T}x}}{1 + e^{\beta^\mathrm{T}x}}1+eβTxeβTx 是对率回归中预测为正例的概率，11+eβTx\frac{1}{1 + e^{\beta^\mathrm{T}x}}1+eβTx1 是预测为负例的概率。
括号内容合并，原式可写为：max⁡（ln⁡(yeβTx+(1−y)1+eβTx)）\max （ \ln \left( \frac{y e^{\beta^\mathrm{T}x} + (1 - y)}{1 + e^{\beta^\mathrm{T}x}} \right) ）max（ln(1+eβTxyeβTx+(1−y))）

括号里边分情况讨论：单样本对数似然项={βTx−ln⁡(1+eβTx=ln⁡eβTx−ln⁡(1+eβTx)=ln⁡eβTx1+eβTx), y=1−ln⁡(1+eβTx=ln⁡1−ln⁡(1+eβTx)=ln⁡11+eβTx), y=0\text{单样本对数似然项} = \begin{cases} \beta^\mathrm{T}x - \ln(1 + e^{\beta^\mathrm{T}x} = \ln e^{\beta^\mathrm{T}x} - \ln(1 + e^{\beta^\mathrm{T}x}) = \ln \frac{e^{\beta^\mathrm{T}x}}{1 + e^{\beta^\mathrm{T}x}} ) & ,\ y = 1 \\ -\ln(1 + e^{\beta^\mathrm{T}x} = \ln 1 - \ln(1 + e^{\beta^\mathrm{T}x}) = \ln \frac{1}{1 + e^{\beta^\mathrm{T}x}}) & ,\ y = 0 \end{cases}单样本对数似然项=⎩ ⎨ ⎧βTx−ln(1+eβTx=lneβTx−ln(1+eβTx)=ln1+eβTxeβTx)−ln(1+eβTx=ln1−ln(1+eβTx)=ln1+eβTx1), y=1, y=0

观察两种情况的结果，可通过 y 来统一表示分子：
- 当 y=1y=1y=1 时，分子为 eβTxe^{\beta^\mathrm{T}x}eβTx；
- 当 y=0y=0y=0 时，分子为 1。
因此，两种情况可统一写成： ln⁡y⋅eβTx+(1−y)⋅11+eβTx\ln \frac{y \cdot e^{\beta^\mathrm{T}x} + (1 - y) \cdot 1}{1 + e^{\beta^\mathrm{T}x}}ln1+eβTxy⋅eβTx+(1−y)⋅1

进一步，利用指数运算的基本性质（如 e0=1e^0 = 1e0=1）和对数的倒数性质（ln⁡ab=−ln⁡ba\ln \frac{a}{b} = -\ln \frac{b}{a}lnba=−lnab ），还可以变成形式： ln⁡1+eβTxeyβTx\ln \frac{1 + e^{\beta^\mathrm{T}x}}{e^{y\beta^\mathrm{T}x}}lneyβTx1+eβTx

3-7、LDA 线性判别分析（Linear Discriminant Analysis）

核心思想：将样例投影到一条直线 （低维空间），使得同类样本的投影尽可能 "近" ，不同类样本的投影尽可能 "远" 。

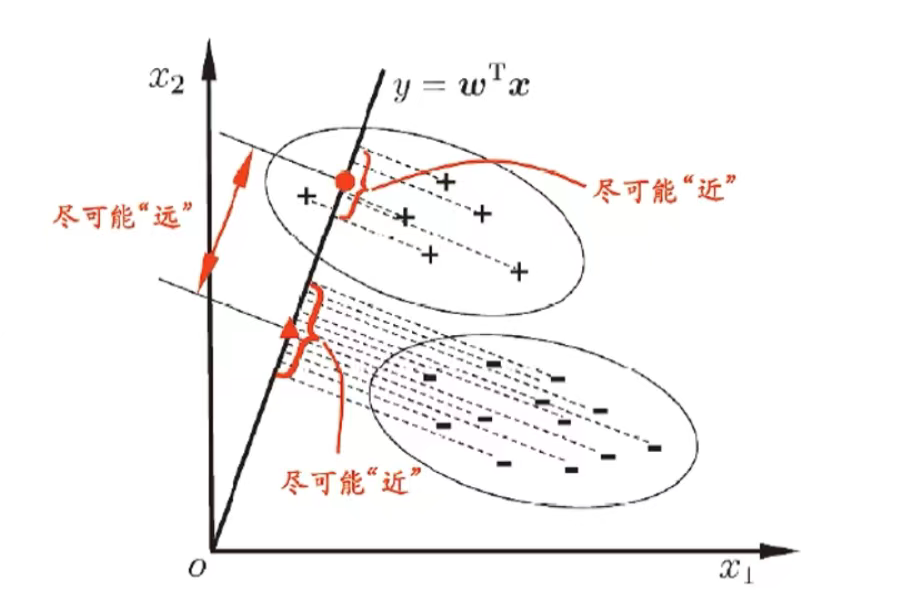
LDA 目标：

给定数据集 (xi,yi)i=1m{(x_i, y_i)}_{i=1}^m(xi,yi)i=1m：

第 iii 类示例的集合 XiX_iXi；
第 iii 类示例的均值向量 μi\mu_iμi；
第 iii 类示例的协方差矩阵 Σi\Sigma_iΣi；
两类样本的中心在直线上的投影：wTμ0w^\mathrm{T}\mu_0wTμ0 和 wTμ1w^\mathrm{T}\mu_1wTμ1 ；
两类样本的协方差：wTΣ0ww^\mathrm{T}\Sigma_0 wwTΣ0w 和 wTΣ1ww^\mathrm{T}\Sigma_1 wwTΣ1w。

LDA的核心目标是：

同类样例的投影点尽可能接近 → wTΣ0w+wTΣ1ww^\mathrm{T}\Sigma_0 w + w^\mathrm{T}\Sigma_1 wwTΣ0w+wTΣ1w 尽可能小；
异类样例的投影点尽可能远离 → ∥wTμ0−wTμ1∥22\|w^\mathrm{T}\mu_0 - w^\mathrm{T}\mu_1\|_2^2∥wTμ0−wTμ1∥22 尽可能大。

因此，需最大化目标函数：求解 www 使目标函数JJJ 最大

J=∥wTμ0−wTμ1∥22wTΣ0w+wTΣ1w=wT(μ0−μ1)(μ0−μ1)TwwT(Σ0+Σ1)w J = \frac{\|w^\mathrm{T}\mu_0 - w^\mathrm{T}\mu_1\|_2^2}{w^\mathrm{T}\Sigma_0 w + w^\mathrm{T}\Sigma_1 w} = \frac{w^\mathrm{T}(\mu_0 - \mu_1)(\mu_0 - \mu_1)^\mathrm{T} w}{w^\mathrm{T}(\Sigma_0 + \Sigma_1) w} J=wTΣ0w+wTΣ1w∥wTμ0−wTμ1∥22=wT(Σ0+Σ1)wwT(μ0−μ1)(μ0−μ1)Tw

LDA的散度矩阵定义：

类内散度矩阵 (within-class scatter matrix)

Sw=Σ0+Σ1=∑x∈X0(x−μ0)(x−μ0)T+∑x∈X1(x−μ1)(x−μ1)T \begin{align*} \mathbf{S}w &= \Sigma_0 + \Sigma_1 \\ &= \sum{x \in X_0} (x - \mu_0)(x - \mu_0)^\mathrm{T} + \sum_{x \in X_1} (x - \mu_1)(x - \mu_1)^\mathrm{T} \end{align*} Sw=Σ0+Σ1=x∈X0∑(x−μ0)(x−μ0)T+x∈X1∑(x−μ1)(x−μ1)T
类间散度矩阵 (between-class scatter matrix)

‍

Sb=(μ0−μ1)(μ0−μ1)T \mathbf{S}_b = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^\mathrm{T} Sb=(μ0−μ1)(μ0−μ1)T
LDA的目标：最大化广义瑞利商 (generalized Rayleigh quotient) 将目标函数用散度矩阵形式替换

J=wTSbwwTSww J = \frac{w^\mathrm{T}\mathbf{S}_b w}{w^\mathrm{T}\mathbf{S}_w w} J=wTSwwwTSbw

最大化目标函数求解思路：

令 wTSww=1\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_w\boldsymbol{w} = 1wTSww=1，最大化广义瑞利商等价形式为：

{min⁡w−wTSbws.t. wTSww=1 \begin{cases} \min\limits_{\boldsymbol{w}} -\boldsymbol{w}^{\mathrm{T}}\mathbf{S}_b\boldsymbol{w} \\ \text{s.t. } \boldsymbol{w}^{\mathrm{T}}\mathbf{S}_w\boldsymbol{w} = 1 \end{cases} {wmin−wTSbws.t. wTSww=1
运用拉格朗日乘子法，有：Sbw=λSww\mathbf{S}_b\boldsymbol{w} = \lambda\mathbf{S}_w\boldsymbol{w}Sbw=λSww
由 Sb\mathbf{S}_bSb 定义，有：Sbw=(μ0−μ1)(μ0−μ1)Tw\mathbf{S}_b\boldsymbol{w} = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^{\mathrm{T}} \boldsymbol{w}Sbw=(μ0−μ1)(μ0−μ1)Tw
注意到 (μ0−μ1)Tw(\mu_0 - \mu_1)^{\mathrm{T}}\boldsymbol{w}(μ0−μ1)Tw 是标量，令其等于 λ\lambdaλ，于是求解结果为： w=Sw−1(μ0−μ1)\boxed{\boldsymbol{w} = \mathbf{S}_w^{-1}(\mu_0 - \mu_1)}w=Sw−1(μ0−μ1) ，标量是大小，但是更加重要的是 " 方向 "
实践中通常进行奇异值分解： Sw=UΣVT\mathbf{S}_w = \mathbf{U}{\Sigma}\mathbf{V}^{\mathrm{T}}Sw=UΣVT，然后：Sw−1=VΣ−1UT\mathbf{S}_w^{-1} = \mathbf{V}{\Sigma}^{-1}\mathbf{U}^{\mathrm{T}}Sw−1=VΣ−1UT

‍

3-8、LDA推广

散度矩阵定义：

全局散度矩阵：St=Sb+Sw=∑i=1m(xi−μ)(xi−μ)T\mathbf{S}_t = \mathbf{S}_b + \mathbf{S}w = \sum{i=1}^{m} (\boldsymbol{x}_i - {\mu})(\boldsymbol{x}_i - {\mu})^TSt=Sb+Sw=∑i=1m(xi−μ)(xi−μ)T
类内散度矩阵：Sw=∑i=1NSwi\mathbf{S}w = \sum{i=1}^{N} \mathbf{S}{w_i}Sw=∑i=1NSwi，其中 Swi=∑x∈Xi(x−μi)(x−μi)T\mathbf{S}{w_i} = \sum_{\boldsymbol{x} \in X_i} (\boldsymbol{x} - {\mu}_i)(\boldsymbol{x} - {\mu}_i)^TSwi=∑x∈Xi(x−μi)(x−μi)T
类间散度矩阵：Sb=St−Sw=∑i=1Nmi(μi−μ)(μi−μ)T\mathbf{S}_b = \mathbf{S}_t - \mathbf{S}w = \sum{i=1}^{N} m_i ({\mu}_i - {\mu})({\mu}_i - {\mu})^TSb=St−Sw=∑i=1Nmi(μi−μ)(μi−μ)T

++多分类LDA有多种实现方法：采用++ ++Sb、St、Sw{S}_b、{S}_t、{S}_wSb、St、Sw++ ++中的任何两个++
多分类LDA优化问题及推导：tr（）表示矩阵的 " 迹 "：方阵 A\mathbf{A}A，它的迹定义为主对角线（从左上角到右下角的对角线）上所有元素的和

max⁡Wtr(WTSbW)tr(WTSwW) ⟹ SbW=λSwW \max_{\mathbf{W}} \frac{\mathrm{tr}\left( \mathbf{W}^{\mathrm{T}}\mathbf{S}_b\mathbf{W} \right)}{\mathrm{tr}\left( \mathbf{W}^{\mathrm{T}}\mathbf{S}_w\mathbf{W} \right)} \implies \mathbf{S}_b\mathbf{W} = \lambda\mathbf{S}_w\mathbf{W} Wmaxtr(WTSwW)tr(WTSbW)⟹SbW=λSwW
广义特征值方程 SbW=λSwW\mathbf{S}_b\mathbf{W} = \lambda \mathbf{S}_w\mathbf{W}SbW=λSwW 可变形为 (Sw−1Sb)W=λW=(Sw−1Sb−λ)W(\mathbf{S}_w^{-1}\mathbf{S}_b)\mathbf{W} = \lambda \mathbf{W} = (\mathbf{S}_w^{-1}\mathbf{S}_b - \lambda )\mathbf{W}(Sw−1Sb)W=λW=(Sw−1Sb−λ)W ，即 λ\lambdaλ 是 Sw−1Sb\mathbf{S}_w^{-1}\mathbf{S}_bSw−1Sb 的特征值， W\mathbf{W}W 的列向量是其特征向量。

其中 W∈Rd×(N−1)\mathbf{W} \in \mathbb{R}^{d \times (N-1)}W∈Rd×(N−1)，W\mathbf{W}W 的闭式解是 Sw−1Sb\mathbf{S}_w^{-1}\mathbf{S}_bSw−1Sb 的 d′d'd′（d′≤N−1d' \leq N-1d′≤N−1）个最大非零广义特征值对应的特征向量组成的矩阵。

（闭式解（Closed-form Solution） 指的是可以通过有限次基本数学运算（如加、减、乘、除、幂、指数、对数、三角函数等） 直接表达出来的解析解。）

‍

3-9、多分类学习基本思路

拆解法：将一个多分类任务拆分为若干个二分类任务求解

OvO（One vs. One）

训练(N(N-1)/2)个分类器，存储开销和测试时间大
训练只用两个类的样例，训练时间短
示例（以4类(C1,C2,C3,C4)(C_1,C_2,C_3,C_4)(C1,C2,C3,C4)为例）：
- ((C1,C2)⇒f1→C1)((C_1, C_2) \Rightarrow f_1 \to C_1)((C1,C2)⇒f1→C1)
- ((C1,C3)⇒f2→C3)((C_1, C_3) \Rightarrow f_2 \to C_3)((C1,C3)⇒f2→C3)
- ((C1,C4)⇒f3→C1)((C_1, C_4) \Rightarrow f_3 \to C_1)((C1,C4)⇒f3→C1)
- ((C2,C3)⇒f4→C3)((C_2, C_3) \Rightarrow f_4 \to C_3)((C2,C3)⇒f4→C3)
- ((C2,C4)⇒f5→C2)((C_2, C_4) \Rightarrow f_5 \to C_2)((C2,C4)⇒f5→C2)
- ((C3,C4)⇒f6→C3)((C_3, C_4) \Rightarrow f_6 \to C_3)((C3,C4)⇒f6→C3)
- 最终结果：通过多个二分类器的投票（如上述示例最终结果为(C3)）(C_3)）(C3)）

OvR（One vs. Rest）

训练(N)个分类器，存储开销和测试时间小
训练用到全部训练样例，训练时间长
示例（以4类(C1,C2,C3,C4)(C_1,C_2,C_3,C_4)(C1,C2,C3,C4)为例）：
- ((C1,C2∪C3∪C4)⇒f1→"−")((C_1, C_2\cup C_3\cup C_4) \Rightarrow f_1 \to "-" )((C1,C2∪C3∪C4)⇒f1→"−")
- ((C2,C1∪C3∪C4)⇒f2→"−")((C_2, C_1\cup C_3\cup C_4) \Rightarrow f_2 \to "-" )((C2,C1∪C3∪C4)⇒f2→"−")
- ((C3,C1∪C2∪C4)⇒f3→"+ ")((C_3, C_1\cup C_2\cup C_4) \Rightarrow f_3 \to "+\ " )((C3,C1∪C2∪C4)⇒f3→"+ ")
- ((C4,C1∪C2∪C3)⇒f4→"−")((C_4, C_1\cup C_2\cup C_3) \Rightarrow f_4 \to "-" )((C4,C1∪C2∪C3)⇒f4→"−")
- 最终结果：选择输出"(+)"的分类器对应的类别（如上述示例最终结果为(C3)）(C_3)）(C3)）

性能对比

预测性能取决于具体数据分布，多数情况下两者差不多

3-10、类别不平衡问题衡 (class--imbalance)

不同类别的样本比例相差很大；"小类"往往更重要

基本思路

原判定逻辑：若 (y1−y>1)(\frac{y}{1-y} > 1)(1−yy>1) 则预测为正例. 此做法默认是取50%，就是大于0.5的部分
类别不平衡下的判定逻辑：若 y1−y>m+m−\frac{y}{1-y} > \frac{m^+}{m^-}1−yy>m−m+ 则预测为正例.

基本策略------"再缩放"(rescaling)

y′1−y′=y1−y×m−m+\frac{y'}{1 - y'} = \frac{y}{1 - y} \times \frac{m^-}{m^+}1−y′y′=1−yy×m+m− 然而，精确估计 m−/m+m^-/m^+m−/m+ 通常很困难！

常见类别不平衡学习方法

过采样 (oversampling) 将类别数目少扩充
例如：SMOTE
欠采样 (undersampling) 将类别数目多的减少
例如：EasyEnsemble
阈值移动 (threshold--moving) 将0.5 移动

‍