二次多项式RSM响应面模型+NSGA-II算法多目标优化，高端绘图（拟合效果图、单因素影响图、交互作用图、三维曲面图）！

MATLAB代码实现了 "基于RSM（响应面分析法）+NSGA-II多目标优化算法的工艺过程定量关系研究"，以下是其简要概述：

---

一、主要功能

1. 数据预处理与建模：基于实验数据建立烧结原料成分（MgO、Al₂O₃、R₂）与SFCA矿物含量之间的定量模型。
2. RSM模型建立：构建二次多项式响应面模型，分析各因素对SFCA含量的影响。
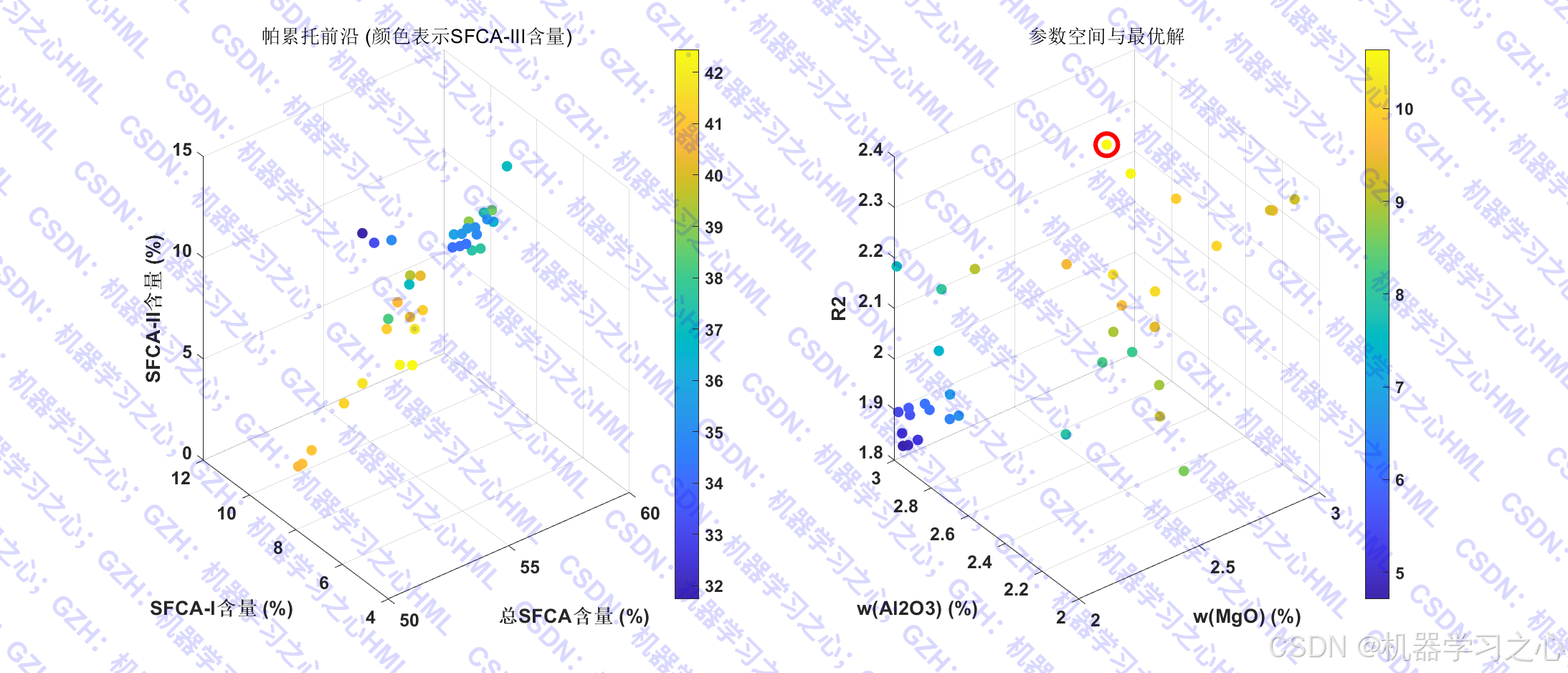
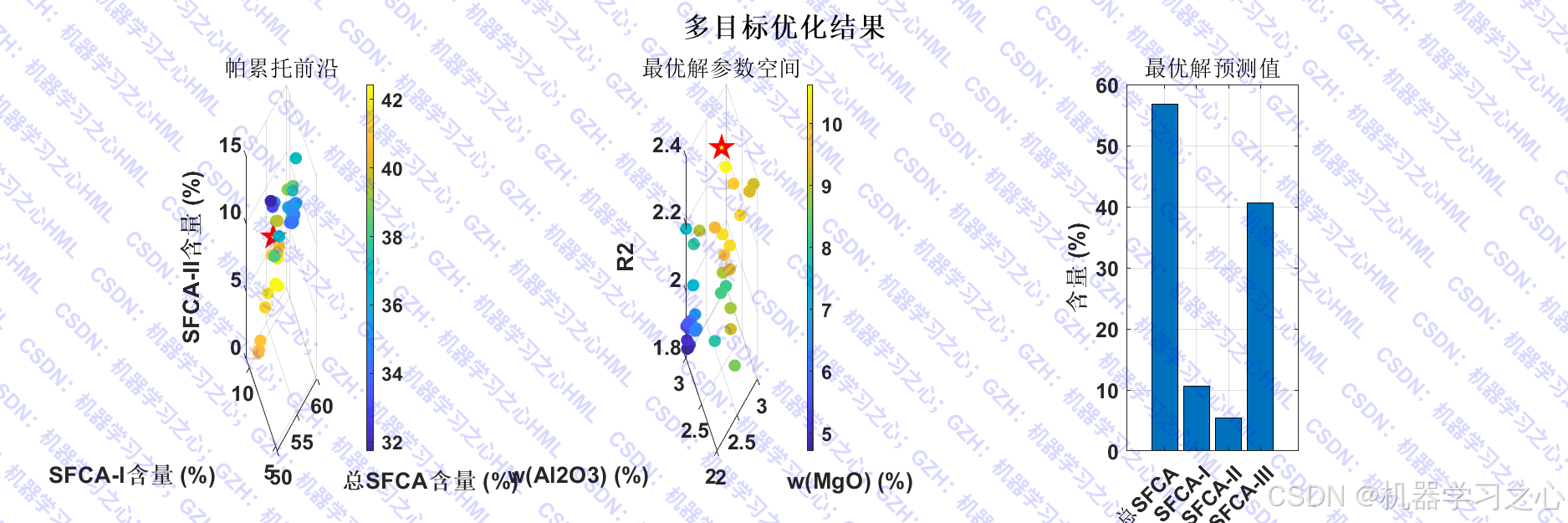
3. 多目标优化：使用NSGA-II算法寻找最优原料配比，最大化总SFCA和SFCA-I，最小化SFCA-II和SFCA-III。
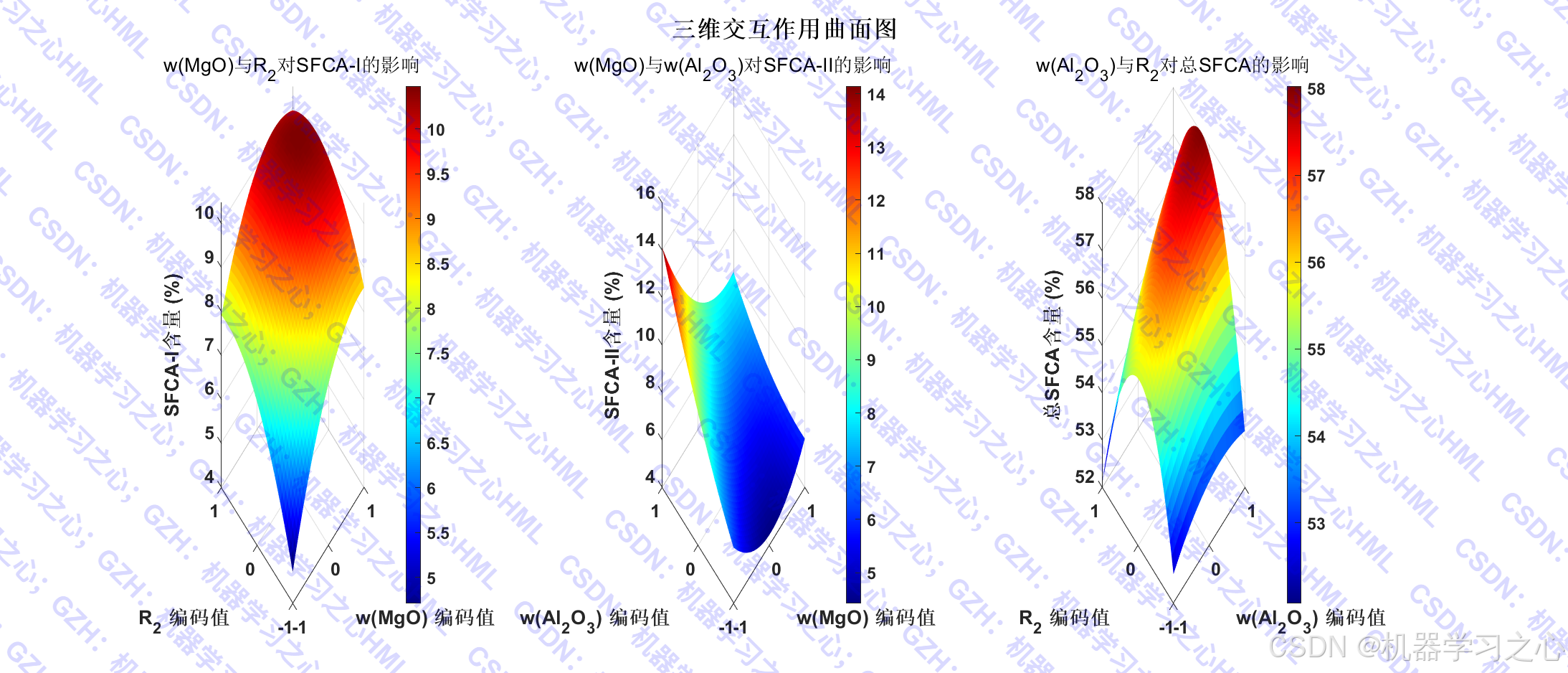
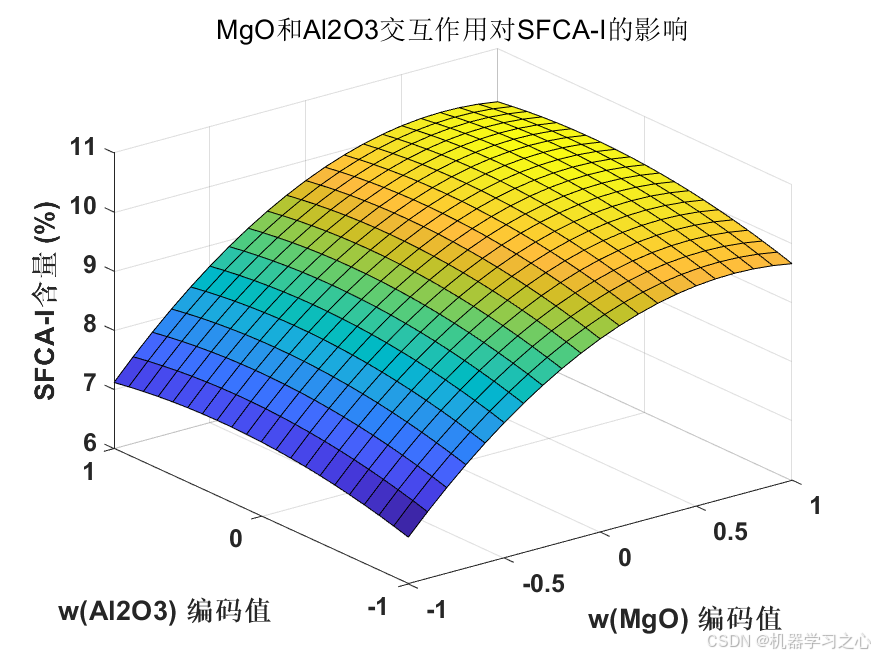
4. 可视化分析：绘制拟合效果图、单因素影响图、交互作用图、三维曲面图等。
5. 模型验证与结果导出：验证模型预测能力，输出优化结果和图形。

---

二、算法步骤

1. 数据导入与编码转换 ：
   • 导入原始配矿方案和矿物组成数据。
   • 将自变量（MgO、Al₂O₃、R₂）转换为编码值（-1, 0, 1）。
2. RSM模型拟合 ：
   • 使用多元线性回归拟合二次多项式模型。
   • 分别建立总SFCA、SFCA-I、SFCA-II、SFCA-III的响应模型。
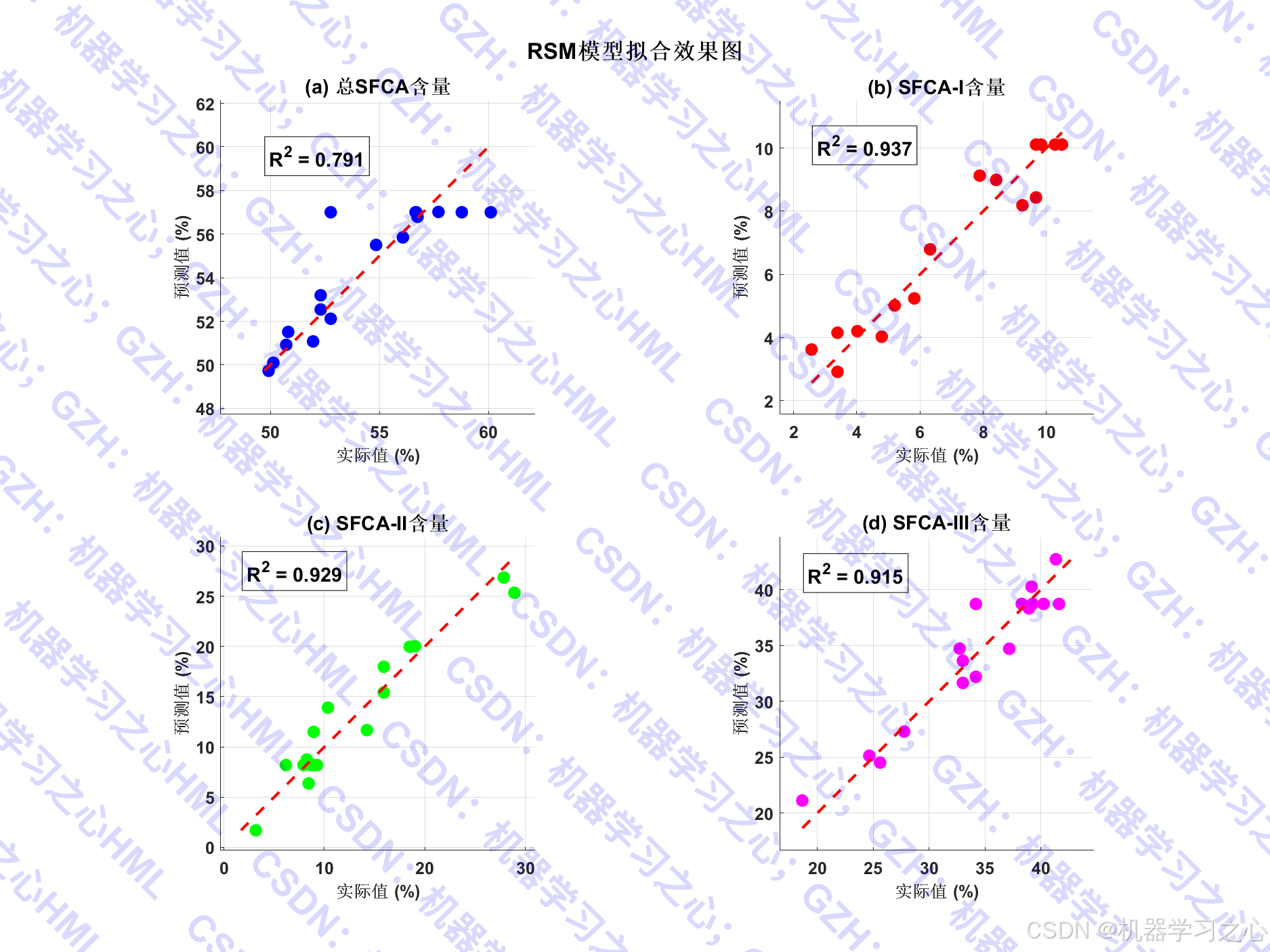
3. 模型评估与可视化 ：
   • 绘制实际值 vs 预测值图。
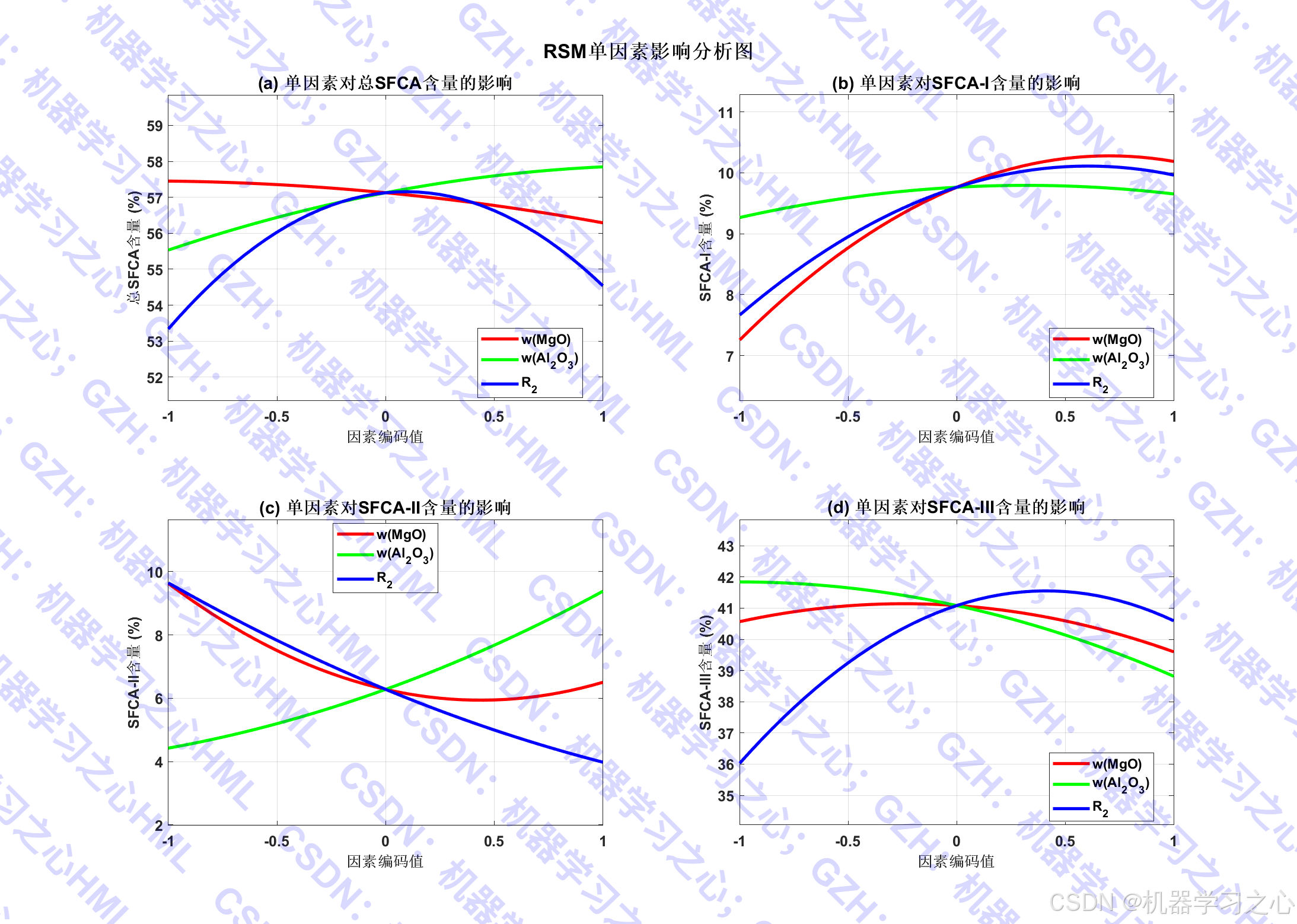
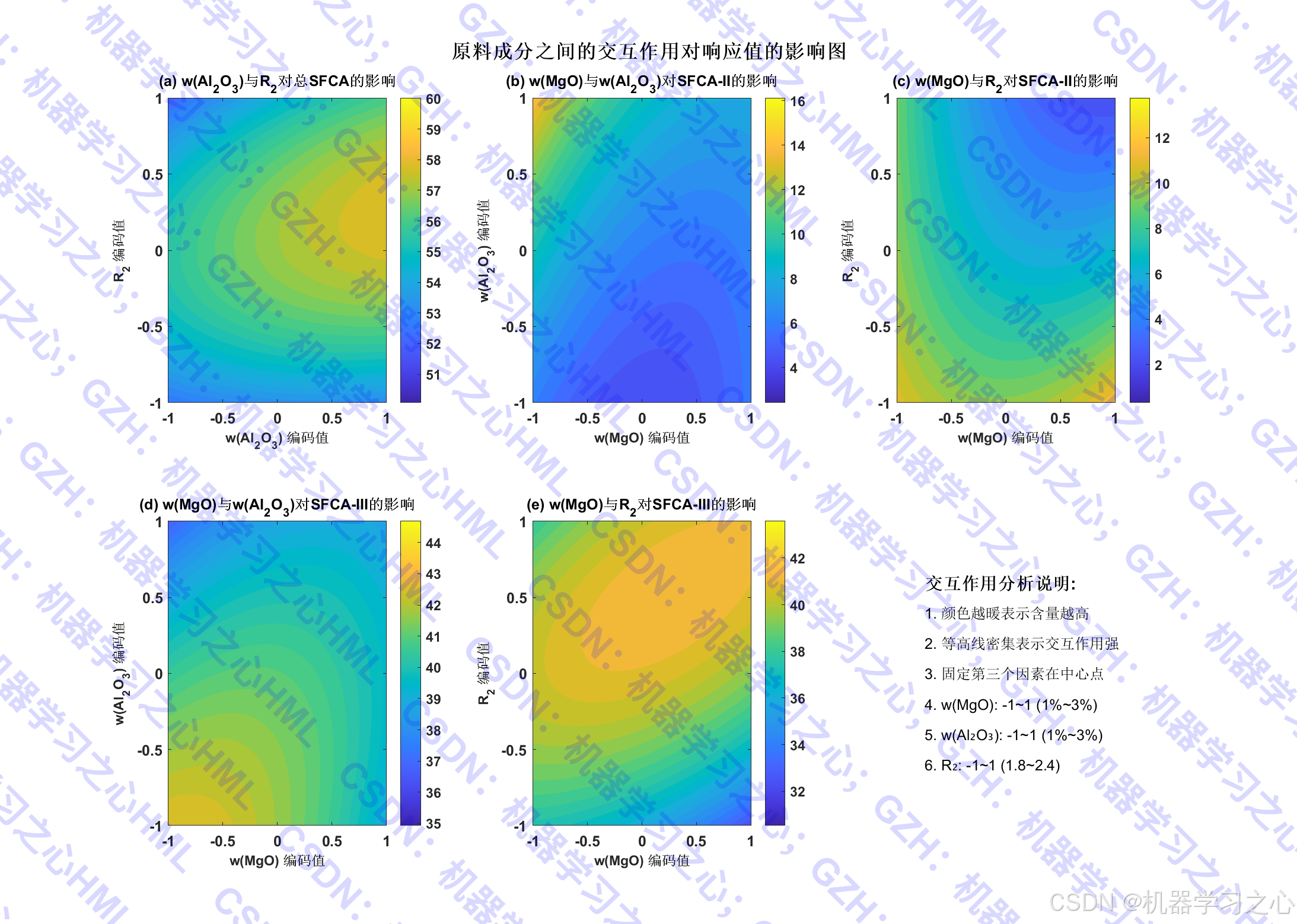
   • 分析单因素影响、交互作用、三维响应面。
4. 灵敏度分析 ：
   • 计算各因素在中心点的灵敏度。
5. 多目标优化（NSGA-II） ：
   • 使用 gamultiobj 函数进行多目标遗传算法优化。
   • 输出帕累托前沿和最优解集。
6. 结果验证与导出 ：
   • 验证论文中给出的最优配比。
   • 导出优化结果表格和所有图形。

---

三、技术路线

数据准备 → RSM建模 → 模型评估 → 单因素与交互分析 → 多目标优化 → 结果验证与输出

---

四、公式原理

1. RSM模型 （二次多项式）：
   Y=β0+∑βiXi+∑βijXiXj+∑βiiXi2+ϵ Y = \beta_0 + \sum \beta_i X_i + \sum \beta_{ij} X_i X_j + \sum \beta_{ii} X_i^2 + \epsilon Y=β0+∑βiXi+∑βijXiXj+∑βiiXi2+ϵ

2. 编码公式 ：

   • MgO、Al₂O₃：Xcoded=2×(Xactual−2)+1X_{\text{coded}} = 2 \times (X_{\text{actual}} - 2) + 1Xcoded=2×(Xactual−2)+1

   • R₂：Xcoded=(Xactual−2.1)/0.3X_{\text{coded}} = (X_{\text{actual}} - 2.1) / 0.3Xcoded=(Xactual−2.1)/0.3

3. 多目标函数 ：
   min⁡−Y1,−Y2,Y3,Y4 \min \left -Y_1, -Y_2, Y_3, Y_4 \\right min−Y1,−Y2,Y3,Y4

---

五、参数设定

参数	说明	取值范围
MgO	质量分数	1%~3%
Al₂O₃	质量分数	1%~3%
R₂	碱度	1.8~2.4
NSGA-II种群大小	100
最大迭代代数	200
帕累托解比例	0.35

---

六、运行环境

• 软件：MATLAB2020+（需安装 Statistics and Machine Learning Toolbox, Global Optimization Toolbox）

---

七、应用场景

1. 冶金工程：烧结工艺优化、配矿方案设计。
2. 材料科学：矿物相组成调控、材料性能预测。
3. 工业优化：多目标配方优化、工艺参数调优。
4. 科研教学：响应面分析、多目标优化算法教学案例。

完整代码私信回复二次多项式RSM响应面模型+NSGA-II算法多目标优化，高端绘图（拟合效果图、单因素影响图、交互作用图、三维曲面图）！