目录
- 前言
- 一、前缀和
-
- [1.1 一维前缀和](#1.1 一维前缀和)
- [1.2 最大子段和](#1.2 最大子段和)
- [1.3 二维前缀和](#1.3 二维前缀和)
- [1.4 激光炸弹](#1.4 激光炸弹)
- 二、差分
-
- [2.1 一维差分](#2.1 一维差分)
- [2.2 海底高铁](#2.2 海底高铁)
- [2.3 二维差分](#2.3 二维差分)
- [2.4 地毯](#2.4 地毯)
- 结语


🎬 云泽Q :个人主页
🔥 专栏传送入口 : 《C语言》《数据结构》《C++》《Linux》《蓝桥杯系列》
⛺️遇见安然遇见你,不负代码不负卿~
前言
大家好啊,我是云泽Q,欢迎阅读我的文章,一名热爱计算机技术的在校大学生,喜欢在课余时间做一些计算机技术的总结性文章,希望我的文章能为你解答困惑~
一、前缀和
前缀和与差分的核心思想是预处理 ,可以在暴力枚举的过程中,快速给出查询的结果,从而优化时间复杂度。由于前缀和和差分在预处理的时候一般需要定义额外的数组来存储预处理的结果,所以前缀和也是经典的用空间替换时间的做法
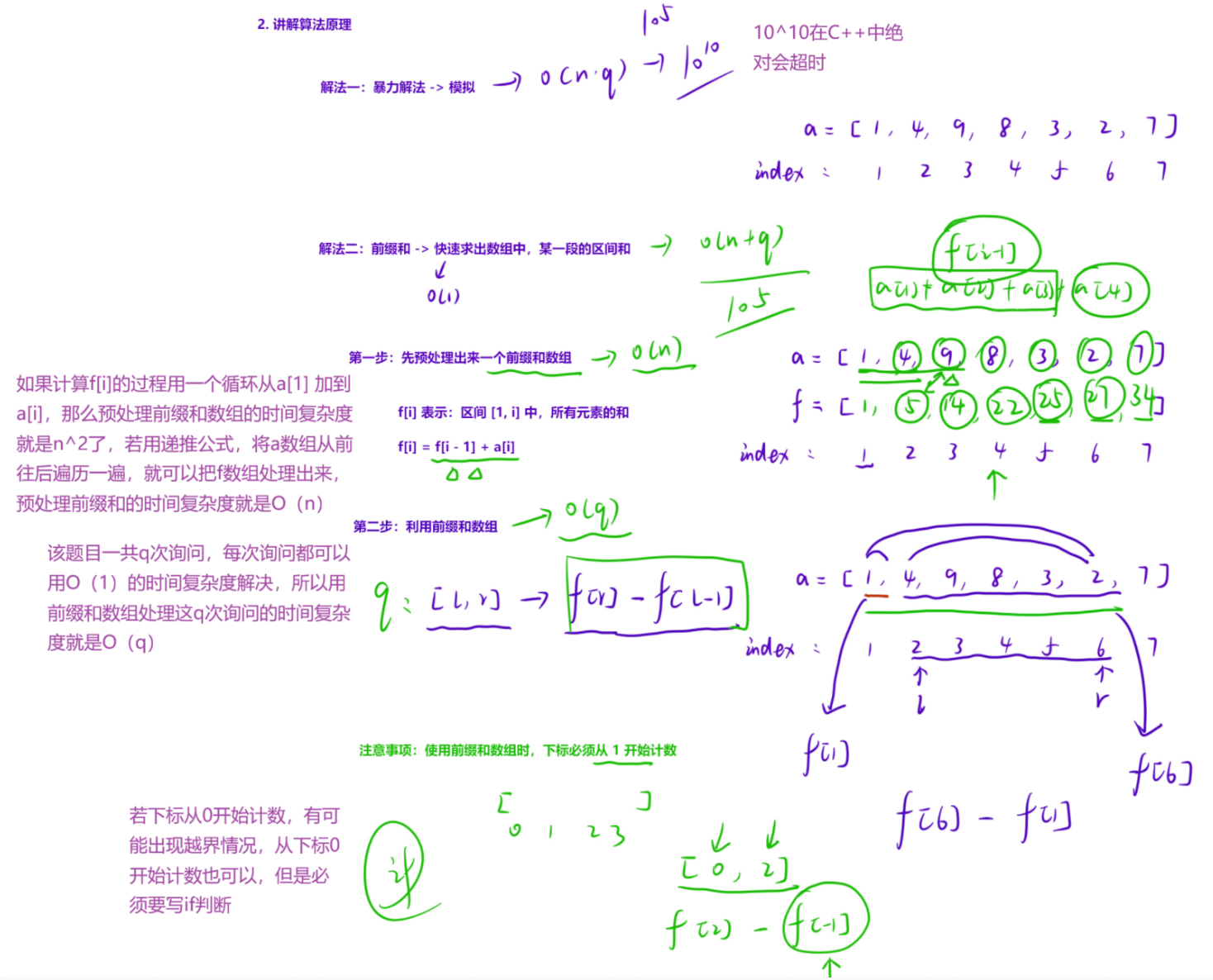
1.1 一维前缀和
cpp
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL a[N], f[N];
int n, m;
int main()
{
cin >> n >> m;
//向初始数组存入数据
for(int i = 1; i <= n; i++) cin >> a[i];
//创建前缀和数组
for(int i = 1; i <= n; i++) f[i] = f[i - 1] + a[i];
//处理m次询问
while(m--)
{
int l, r; cin >> l >> r;
cout << f[r] - f[l - 1] << endl;
}
return 0;
}1.2 最大子段和
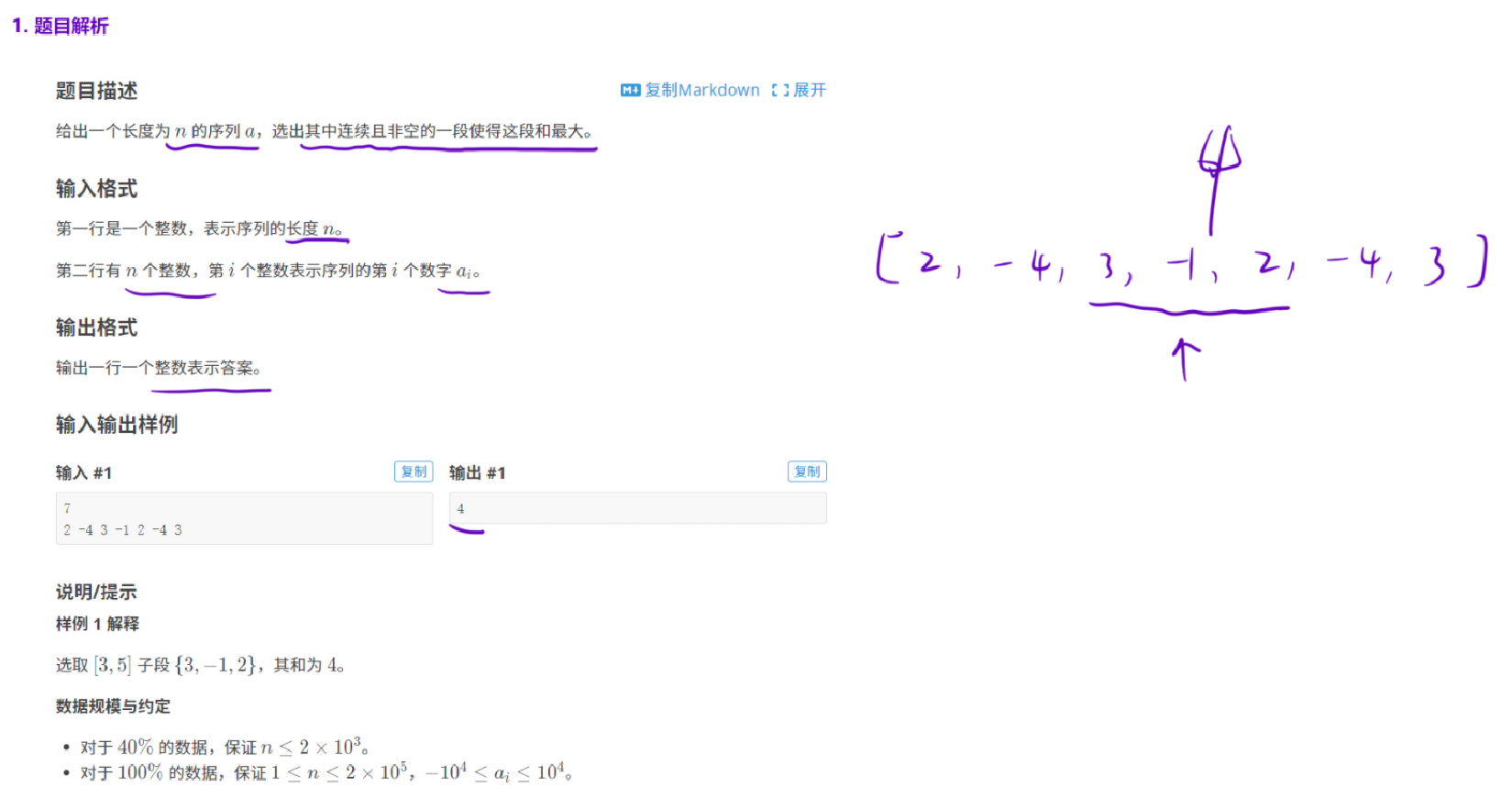
最大子段和
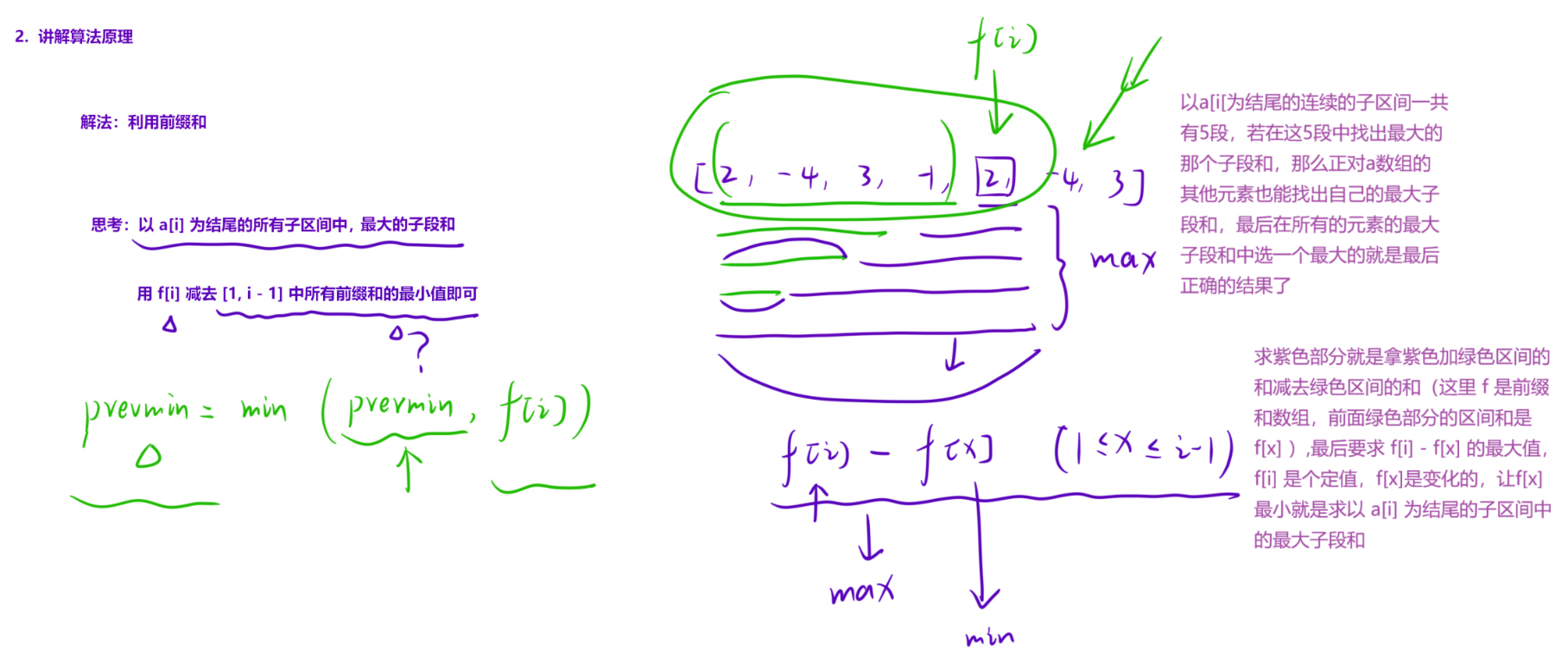
解法
这道题解法有多种,这里介绍前缀和 解法。
考虑以 i 位置的元素 a[i] 为结尾的最大子段和:
- 在求区间和时,相当于是用 f[i] 减去 i 位置前面的某一个 f[x]
- 如果想要最大子段和 ,也就是最大区间和 ,那么用 f[i] 减掉一个前驱最小值即可
因此可以创建 a 数组的 前缀和 数组,然后在遍历前缀和数组的过程中,一边更新前驱最小值 ,一边更新当前位置为结尾的最大子段和
cpp
#include <iostream>
using namespace std;
typedef long long LL; // 避免溢出
const int N = 2e5 + 10; // 数组大小
int n;
LL f[N]; // f[i]:前i个数的前缀和
int main()
{
cin >> n;
// 第一步:计算前缀和数组f
for(int i = 1; i <= n; i++)
{
LL x; cin >> x; // 读入序列的第i个数a[i]
f[i] = f[i - 1] + x; // 前缀和递推:f[i] = 前i-1项和 + 当前项
}
LL ret = -1e20; // 存储最终答案,初始化为极小值(避免全负数的情况)
LL prevmin = 0; // 维护前k项前缀和的最小值(初始为f[0]=0)
// 第二步:遍历每个元素,计算最大子段和
for(int i = 1; i <= n; i++)
{
// 以i结尾的最大子段和 = f[i] - 前i-1项中最小的f[k]
ret = max(ret, f[i] - prevmin);
// 更新前缀最小值:把当前f[i]加入候选,取更小值
prevmin = min(prevmin, f[i]);
}
cout << ret << endl;
return 0;
}样例模拟(以题目样例为例)
样例输入:
cpp
7
2 -4 3 -1 2 -4 3步骤 1:计算前缀和数组 f
规定 f[0] = 0,则:
- f[1] = f[0] + 2 = 2
- f[2] = f[1] + (-4) = -2
- f[3] = f[2] + 3 = 1
- f[4] = f[3] + (-1) = 0
- f[5] = f[4] + 2 = 2
- f[6] = f[5] + (-4) = -2
- f[7] = f[6] + 3 = 1
步骤 2:遍历计算最大子段和
初始化 ret = -1e20,prevmin = 0(即 f[0]):
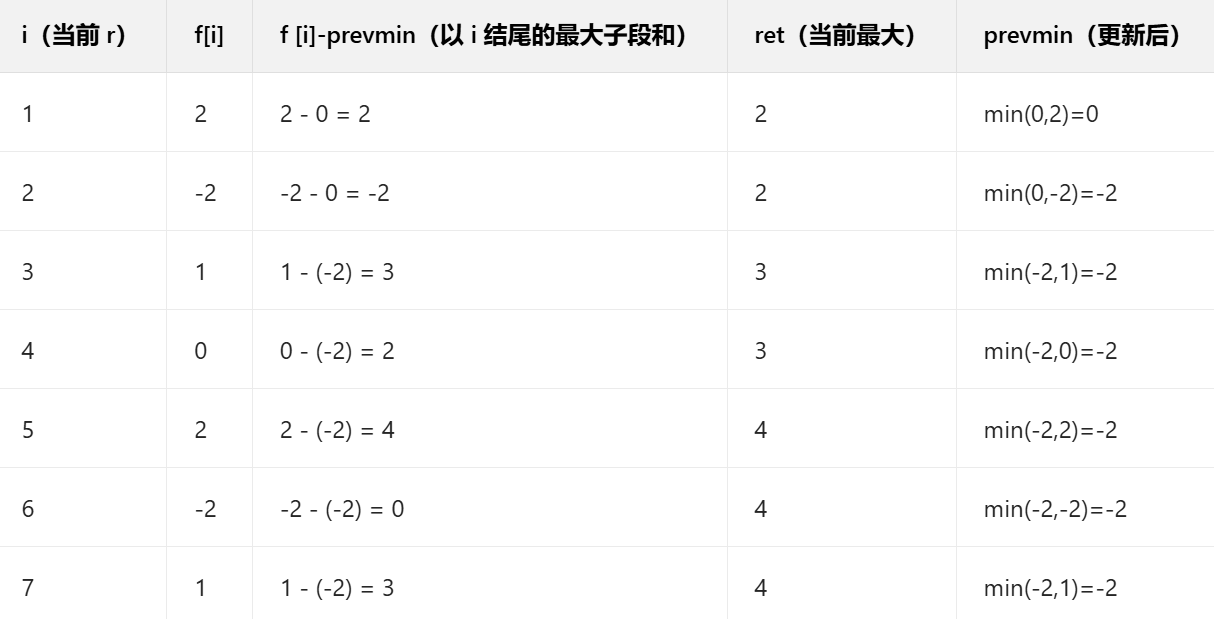
补充几点
- 数据类型必须用 long long:序列中每个数的范围是 -1e4 ~ 1e4,n=2e5 时,最大可能和为 2e5 × 1e4 = 2e9,超过了 int 的范围(int 最大为 231-1=2147483647≈2e9,刚好卡边界,实际会溢出),因此必须用 long long 存储前缀和与结果。
下面是最大和为2e9的场景
整个序列的所有元素都是最大值 1e4,且我们选择的子段是 "整个序列"(因为全是正数,越长和越大)。
此时子段和 = 元素个数 × 单个元素最大值,代入最大值计算:
- 元素个数取最大:2×10⁵(2e5);
- 单个元素取最大:1×10⁴(1e4);
- 相乘得:2×10⁵ × 1×10⁴ = 2×10⁹(2e9,也就是 2000000000)。
-
ret用于统计所有情况下的最大值,初始情况下初始化为无穷小,切记不能初始化为0,因为数组中的有些数是小于0的,若数组中的所有数都小于0,也就是说最小子段和是个负数,取max最终结果就会是0
-
在计算数组中第一个元素的最小子段和时,其前面是没有前缀和的,默认这个前缀和为0
1.3 二维前缀和
【模板】二维前缀和
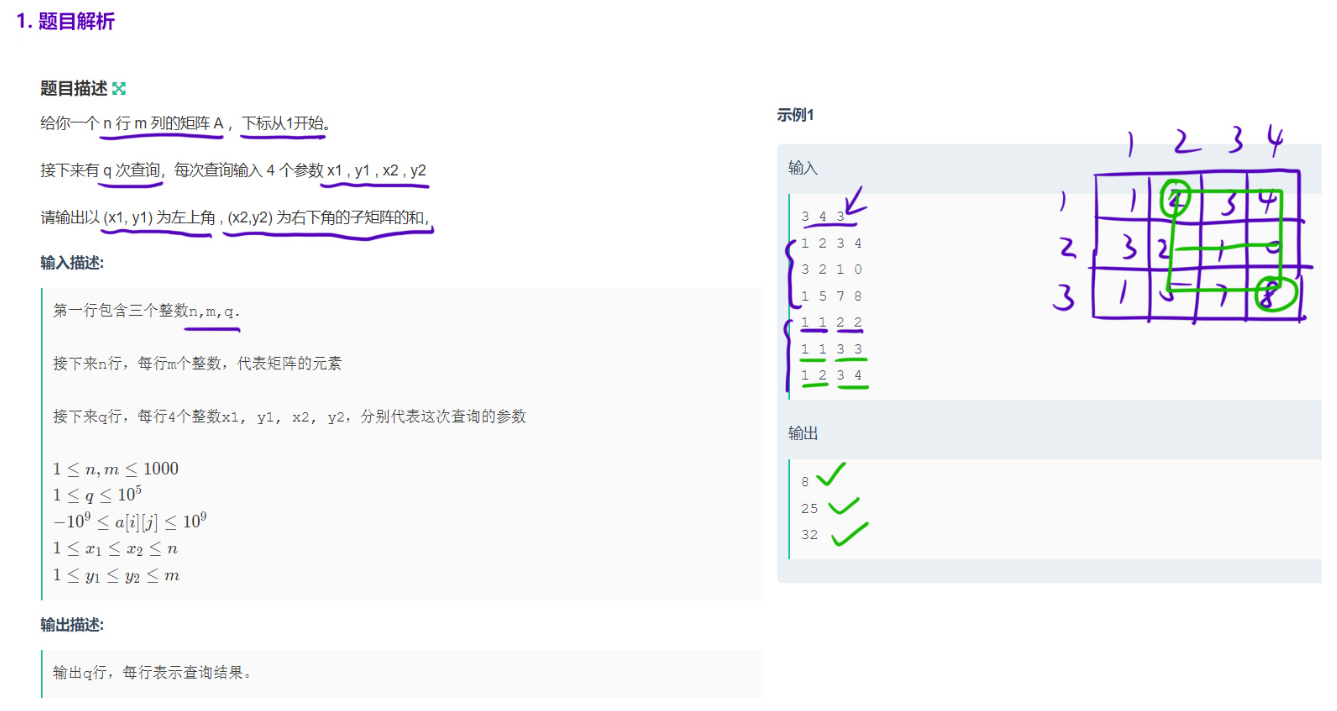
解法
二维前缀和模板题,直接套用公式 创建前缀和矩阵,然后利用前缀和矩阵的性质处理q次访问
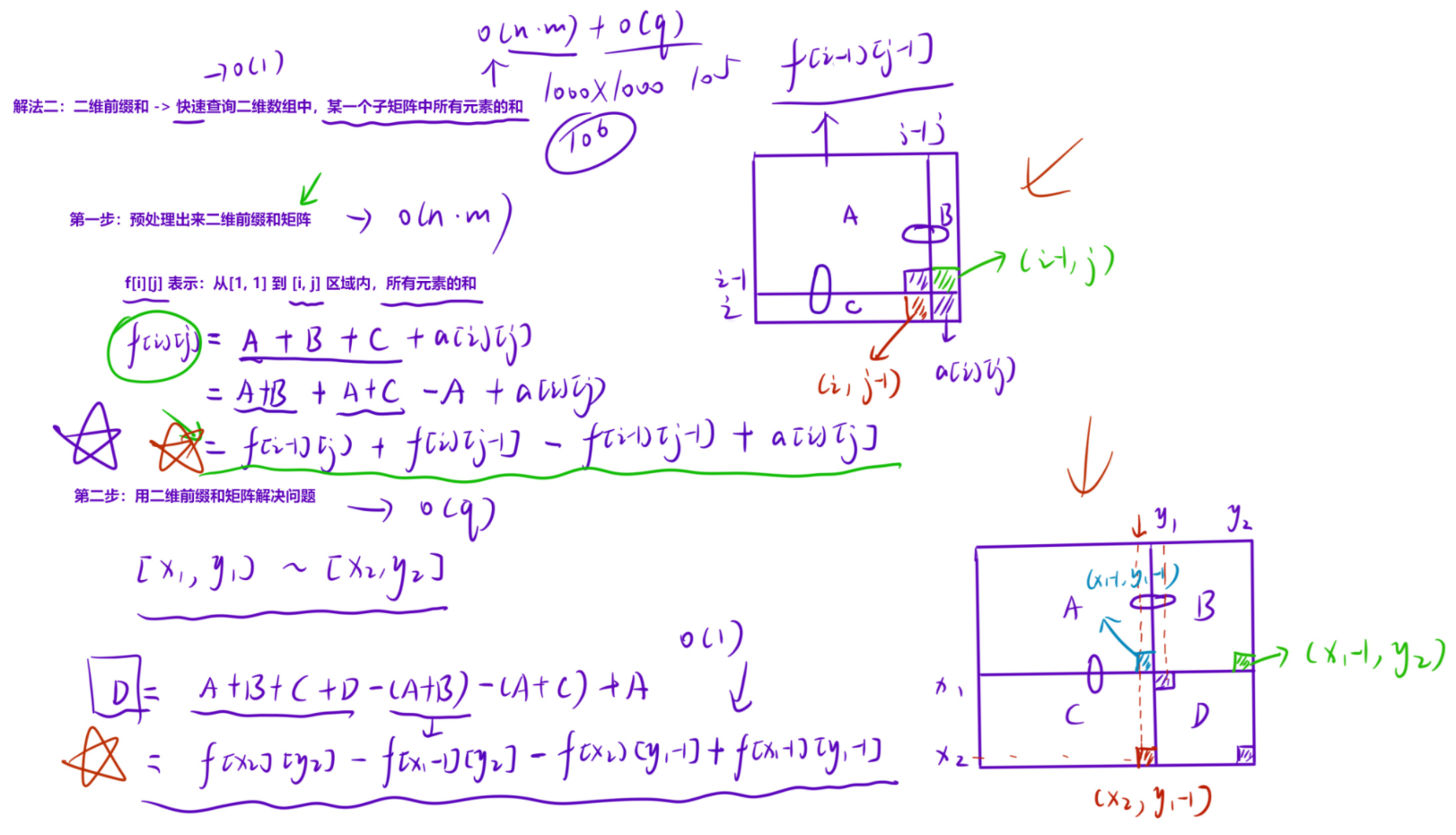
-
创建前缀和矩阵:f[i][j] = f[i - 1][j] + f[i][j - 1] -f[i - 1][j - 1] + a[i][j]

-
查询以(x1, y1)为左上角,(x2,y2)为右下角的子矩阵的和
cpp
#include<iostream>
using namespace std;
const int N = 1010;
typedef long long LL;
int n, m, q;
LL f[N][N];
int main()
{
cin >> n >> m >> q;
//预处理前缀和矩阵
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
LL x; cin >> x;
f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + x;
}
}
//处理q次查询
while(q--)
{
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1] << endl;
}
return 0;
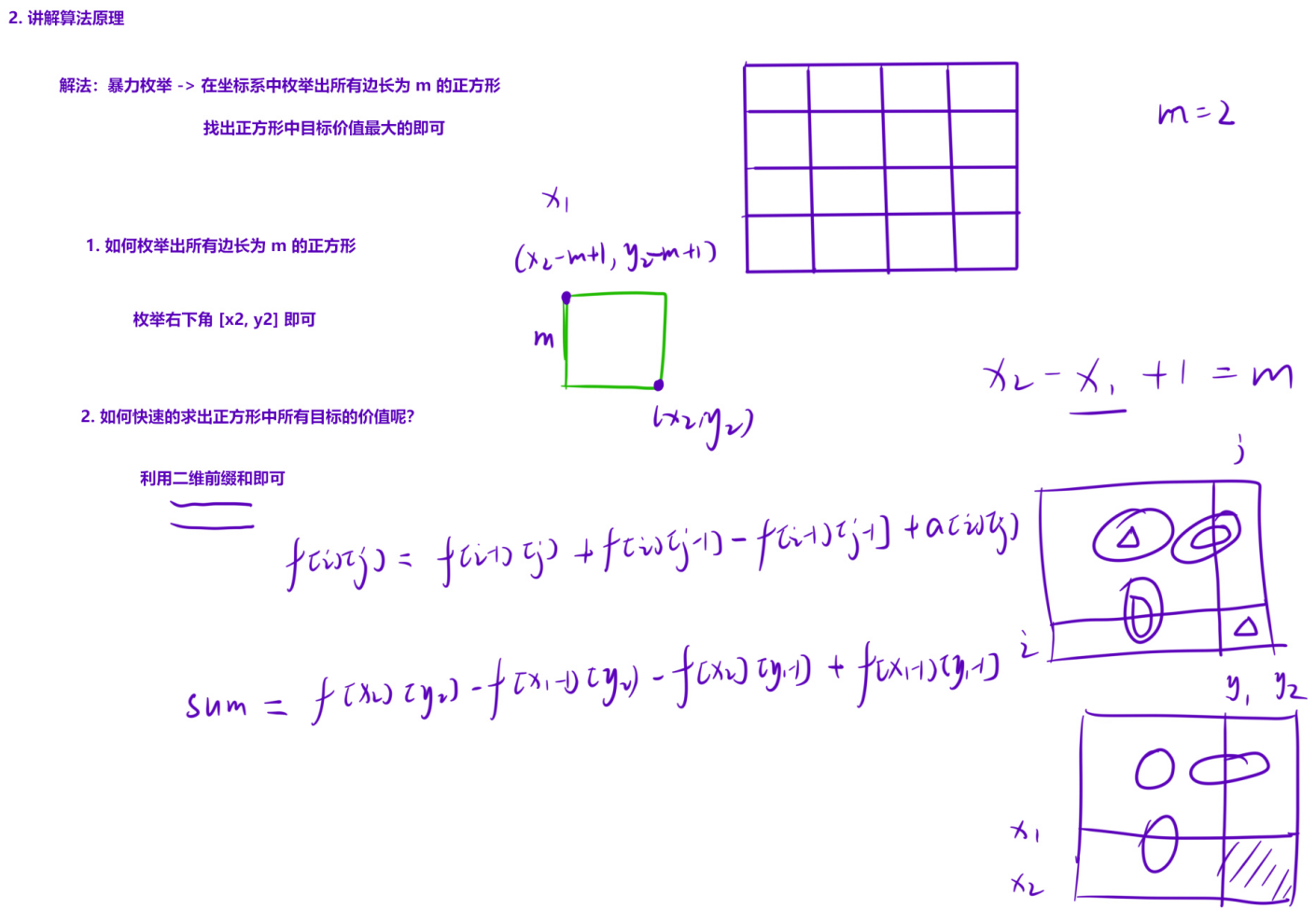
}1.4 激光炸弹
cpp
#include<iostream>
using namespace std;
// 数组最大尺寸
const int N = 5010;
// n:初始表示目标点的数量,后续复用为前缀和矩阵的最大有效下标;m:爆破正方形的边长
int n, m;
int a[N][N];// 存储每个坐标点的目标总价值(同一坐标可能有多个目标,价值累加)
int f[N][N];// 二维前缀和矩阵,用于快速计算任意矩形区域的总价值
int main()
{
cin >> n >> m;
// 循环读取每个目标点的信息
while(n--)
{
int x, y, v; // x/y:目标原始坐标,v:该目标的价值
cin >> x >> y >> v;
// 坐标转为1-based(避免前缀和计算时i-1/j-1越界)
x++; y++;
a[x][y] += v; // 同一坐标多个目标,价值累加
}
// 前缀和矩阵的有效范围:原始坐标0~5000 → 1-based后1~5001
n = 5001;
// 构建二维前缀和矩阵
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
}
}
int ret = 0; // 记录爆破正方形能覆盖的最大目标总价值
m = min(n, m); // 防止正方形边长超过矩阵有效范围
// 暴力枚举所有边长为m的正方形(枚举右下角坐标(x2,y2))
for(int x2 = m; x2 <= n; x2++)
{
for(int y2 = m; y2 <= n; y2++)
{
// 由右下角坐标推导左上角坐标
int x1 = x2 - m + 1, y1 = y2 - m + 1;
ret = max(ret, f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1]);
}
}
// 输出最大可爆破的目标总价值
cout << ret << endl;
return 0;
}这里说一下:为什么知道正方形的右下角下标若等于(x2,y2),其左上角下标为(x2 - m + 1,y2 - m + 1)

二、差分
2.1 一维差分
2.2 海底高铁
2.3 二维差分
2.4 地毯
结语