92.基于matlab的KPCA的TE过程的故障监测，利用核主元分析法(KPCA)来进行故障检...

92.基于matlab的KPCA的TE过程的故障监测，利用核主元分析法(KPCA)来进行故障检测的思想,将输入空间中复杂的非线性问题转化为特征空间中的线性问题，计算步骤：（1）选择监控变量，收集正常工况下的各变量的样本；(2)特征分解,求得特征值;（3）确定主元个数;（4）计算T2统计量控制限和SPE统计量控制限。程序已调通，可直接运行。

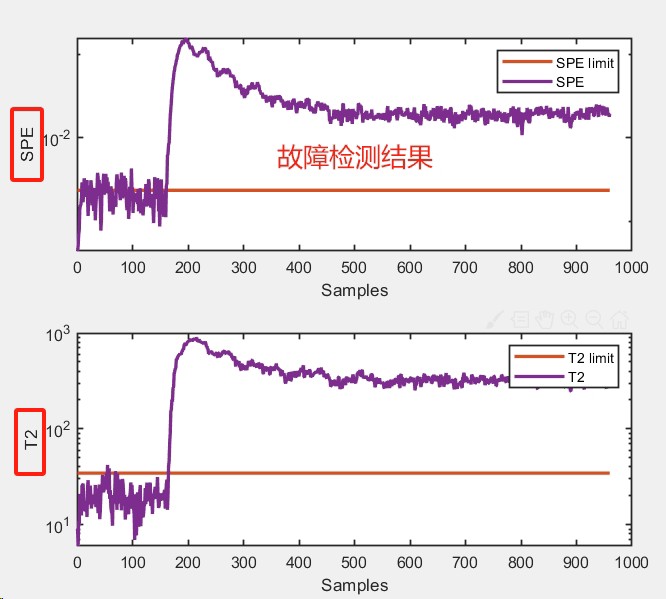
今天我们来聊聊基于Matlab的KPCA（核主元分析法）在TE过程故障监测中的应用。KPCA是一种强大的工具，它能够将复杂的非线性问题转化为特征空间中的线性问题，从而简化故障检测的过程。

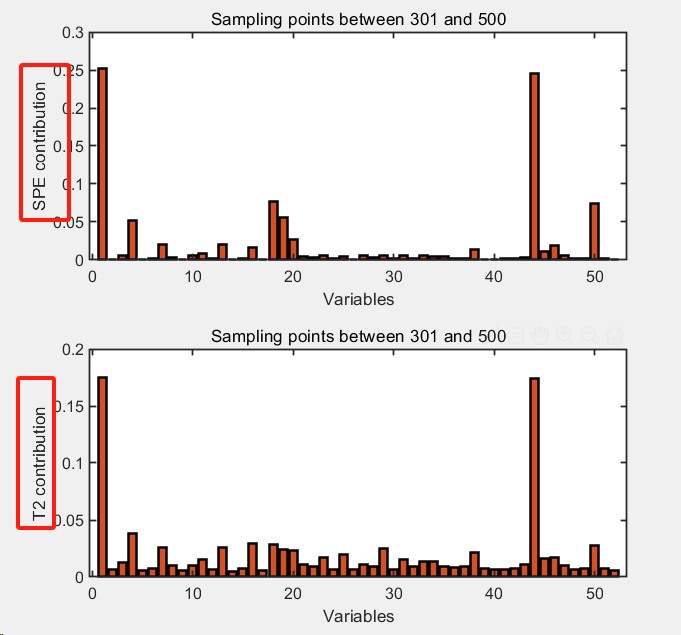
首先，我们需要选择监控变量，并收集正常工况下的各变量样本。这一步是基础，确保我们有足够的数据来训练模型。接下来，我们进行特征分解，求得特征值。这一步是KPCA的核心，它帮助我们理解数据的内在结构。

matlab 复制代码

% 假设我们有一个数据矩阵X，每一行是一个样本，每一列是一个变量
X = load('normal_operation_data.mat'); % 加载正常工况数据
K = kernel(X, 'gaussian', 1); % 使用高斯核函数计算核矩阵
[V, D] = eig(K); % 特征分解，V是特征向量，D是特征值

在特征分解之后，我们需要确定主元个数。这一步有点像是挑选出最重要的特征，帮助我们减少数据的维度，同时保留最重要的信息。

matlab 复制代码

% 确定主元个数
eigenvalues = diag(D);
cumulative_variance = cumsum(eigenvalues) / sum(eigenvalues);
num_components = find(cumulative_variance >= 0.95, 1); % 保留95%的方差

最后，我们计算T2统计量控制限和SPE统计量控制限。这两个统计量帮助我们判断新的数据是否偏离了正常工况，从而检测出潜在的故障。

matlab 复制代码

% 计算T2统计量控制限
T2_limit = num_components * (size(X, 1) - 1) / (size(X, 1) - num_components) * finv(0.95, num_components, size(X, 1) - num_components);

% 计算SPE统计量控制限
SPE_limit = chi2inv(0.95, size(X, 2) - num_components);

通过以上步骤，我们就可以利用KPCA进行TE过程的故障监测了。这个程序已经调通，可以直接运行，希望对大家有所帮助。如果你有任何问题或想法，欢迎在评论区留言讨论！