算法学习入门---stack（C++）

目录

1.stack介绍

2.洛谷---【模板】栈

3.leetcode---有效的括号

4.洛谷---【深基15.习9】验证栈序列

5.洛谷---后缀表达式

6.洛谷---括号序列

---

1.stack介绍

#include<iostream>
#include<stack>
using namespace std;

int main()
{
	stack<int> st;
	
	//先将 1~10 进栈
	for(int i=1;i<=10;i++)
		st.push(i);	
	while(!st.empty())//也可以写成st.size()
	{
		cout<<st.top()<<" ";
		st.pop();	
	} 
	return 0;
}

stack是c++ stl 库当中的一种模板，是实现了栈的功能。

以下是stack模板的一些常用函数：

• 初始化：stack<size> stack_name
• push：入栈
• pop：出栈
• top：返回栈顶元素
• empty：为空栈返回true，非空返回false
• size：返回栈内元素个数

2.洛谷---【模板】栈

因为有多组测试数据，所以每组数据输入完以后需要清空；因为stack模板没有现成的clear函数，所以可以自定义一个clear函数

代码：

#include<iostream>
#include<stack>
using namespace std;
#define int unsigned long long int

void clear(stack<int>& st)//清空st栈 
{
	while(!st.empty()) st.pop();
}

signed main()
{
	int T;cin>>T;
	stack<int> st;
	while(T--)
	{
		clear(st);
		int n;
		cin>>n;
		while(n--)
		{
			string in;cin>>in;
			if(in == "push")
			{
				int num;cin>>num;
				st.push(num);
			}
			if(in == "pop")
			{
				if(st.empty()) cout<<"Empty"<<endl;
				else st.pop();
			}
			if(in == "query")
			{
				if(st.empty()) cout<<"Anguei!"<<endl;
				else cout<<st.top()<<endl;	
			} 
			if(in == "size") cout<<st.size()<<endl;
		}
	}
	return 0;
}

代码易错点：因为数据最大的情况下能达到 2^ 64，所以 long long 类型也存不下，必须使用 unsigned long long 类型来存储

3.leetcode---有效的括号

栈的经典模板题，提问括号与括号之间是否能够相互匹配，需要注意的是：{ ( ) } 这种也算是有效的括号

---

比如 { ( ) } 这个例子，根据stack先进后出的特点，放在栈顶的永远是最后一个进入的元素，同时出栈的也永远是栈顶元素；那么，( 在栈顶的时候，) 入栈就能与其抵消，这两个同时出栈以后，栈顶元素就变为了 { ，然后 } 又与 { 抵消，成功模拟了这种情况

最后需要判断栈是否为空，如果为空才是全部匹配完毕了

如果能够相互匹配，返回true；如果不能相互匹配，返回false

代码：

class Solution {
public:
    bool isValid(string s) {
        stack<char> st;
        for(auto ch:s)
        {
            //判断是否为左符号
            if(ch=='('||ch=='['||ch=='{') st.push(ch);
            else
            {
                if(st.empty())return false;//右符号为字符串中的第一个
                char flag = st.top();
                if(ch==')'&&flag!='(') return false;
                if(ch==']'&&flag!='[') return false;
                if(ch=='}'&&flag!='{') return false;
                st.pop();
            }
        }
        if(st.empty()) return true;
        return false;
    }
};

4.洛谷---【深基15.习9】验证栈序列

判断入栈序列pushed与出栈序列poped是否能匹配上

每次入栈都与出栈序列进行一次比对，如果全部入栈完并一一出栈以后，栈不为空说明无法匹对，返回false

#include<iostream>
#include<stack>
#include<string.h>
using namespace std;

const int N = 1e5 + 10;
int pushed[N],poped[N];

bool isValid(int n)
{
	stack<int> st;
	int cur=0;//统计当前位于出栈队列的什么位置 
	for(int i=0;i<n;i++)
	{
			while(!st.empty())//判断当前栈中是否有元素能够出栈 
			{
				int ele_1 = st.top();
				int ele_2 = poped[cur];
				if(ele_1==ele_2) //说明有东西能够出栈
				{
					st.pop();
					cur++;	
				} 
				else break;
			}
			st.push(pushed[i]);
	}//进栈完毕，判断是否可以和出栈序列匹配 
	for(int i=cur;i<n;i++)
	{
		int right = poped[i];
		int left = st.top();
		if(left!=right) return false;
		else st.pop();
	}
	return true;
}

int main()
{
	int q;cin>>q;
	while(q--)
	{
		memset(pushed,0,sizeof(pushed));
		memset(poped,0,sizeof(poped));
		int n;cin>>n;
		for(int i=0;i<n;i++)
			cin>>pushed[i];
		for(int i=0;i<n;i++)
			cin>>poped[i];
		if(isValid(n)) cout<<"Yes"<<endl;
		else cout<<"No"<<endl;
	}
	return 0;
}

代码易错点：每次进完栈应该要对整个栈进行一次出栈入栈序列的匹对操作，要不然会有元素应该可以出栈的，当前没有出栈，从而导致了结果的错误

5.洛谷---后缀表达式

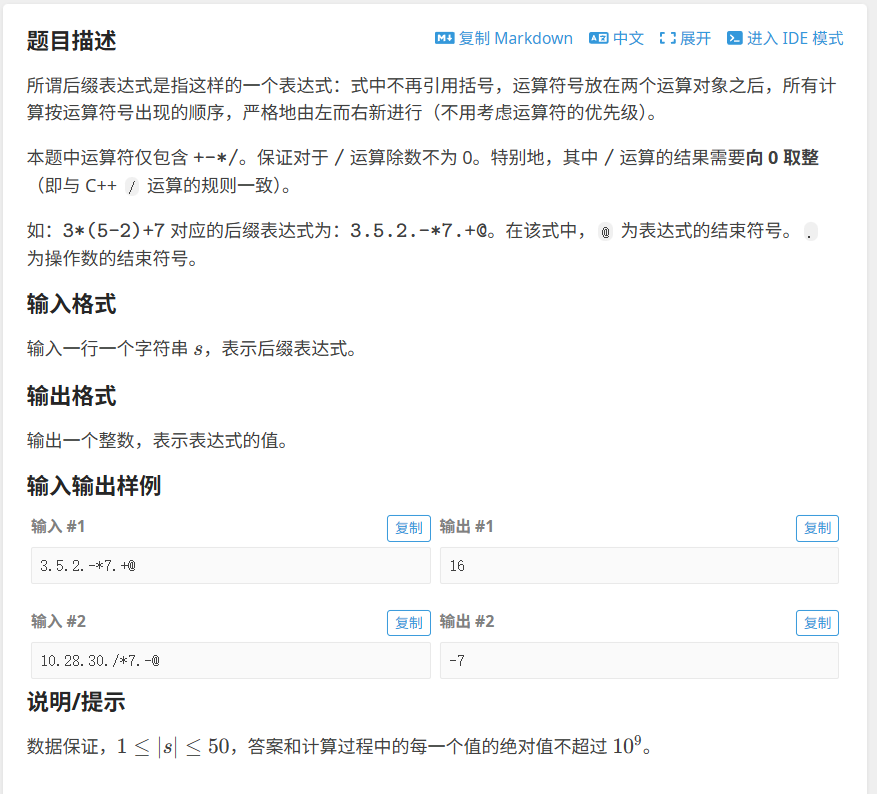
什么是后缀表达式？

后缀表达式又被叫做逆波兰表达式，在计算机中先把表达式转换为后缀表达式，然后对后缀表达式求值就可以丢掉所有的括号了，所以编译系统在编译的时候都会进行这一步操作

---

(5-2) -> 5,2,-

3 × (5-2) -> 3,5,2,-,×

3 × (5-2) + 7 -> 3,5,2,-,×,7,+

通过上述规律，不难发现可以把一个表达式或者一个单一的数看作一个操作数，操作符左边的操作数放在后缀表达式的左边，操作符右边的操作数放在后缀表达式的右边，最后在后缀表达式跟上一个操作符即可（图解如下图所示）

---

利用栈来模拟计算流程：

1. 遇到数，直接进栈
2. 遇到操作符，弹出两个栈顶元素，第一个弹出的为right（最新放入的数，所以在操作符右边），第二个弹出的为left

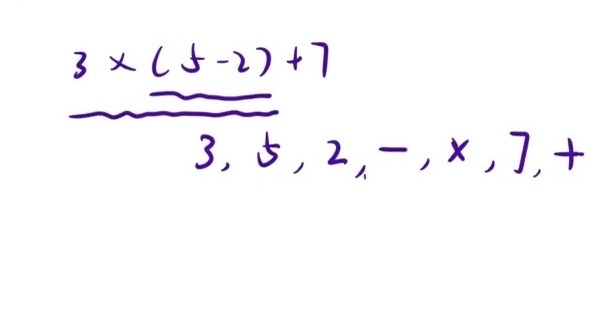
代码：

#include<iostream>
#include<stack>
#include<string>
using namespace std;


int main()
{
	char ch;
	stack<int> st;
	int num = 0;
	while(cin>>ch)
	{
		if(ch == '@')break;
		if(ch == '.')//存放数据 
		{
			if(num)st.push(num);
			num = 0;	
		}
		else if(ch>='0'&&ch<='9')//统计数据 
		{
			num = num*10 + (ch-'0');
		}
		else//开始运算 
		{
			int right = st.top();st.pop();
			int left = st.top();st.pop();
			int ret;
			if(ch=='-')ret = left - right;
			else if(ch=='*')ret = left*right;
			else if(ch=='/')ret = left/right;
			else ret = left+right;
			st.push(ret);
		}
	}
	cout<<st.top();
	return 0;
}

6.洛谷---括号序列

对于当前的字符，如果它是一个右括号，考察它与它左侧离它最近 的未匹配 的的左括号。这也就是为什么示例二的输出是( ) [ ] ( )，而不是( [ ] )

与第三题括号匹配大同小异，定义一个bool数组来判断是否需要在最后结果补括号（匹配为1，不匹配为0） ，为了确定是字符串的哪一个位置字符不匹配，所以在栈中存放左括号的下标

---

通过本题，我们可以看到一个解题技巧：当需要判断数组中某一数据是否需要进行某种操作时，可以通过一个下标与之对应的bool数组来判断

代码：

#include<iostream>
#include<stack>
#include<string>
using namespace std;

const int N = 110;

bool flag[N];

int main()
{
	string s;cin>>s;
	stack<int> st;
	for(int i=0;i<s.size();i++)
	{
		char ch = s[i];
		if(ch=='('||ch=='[') st.push(i);
		else
		{
			//右括号
			if(st.empty()) continue;
			int index = st.top();
			char left = s[index];
			if((left=='('&&ch==')')||(left=='['&&ch==']'))//匹配成功，出栈+bool数组
			{
				st.pop();
				flag[index] = flag[i] = true;	
			} 
		}
	}
	//还原数组
	string ret; 
	for(int i=0;i<s.size();i++)
	{
		char ch = s[i];
		//可以匹配
		if(flag[i]) ret+=ch;
		else
		{
			if(ch=='(') 
			{
				ret+=ch;
				ret+=')';
			}
			else if(ch==')')
			{
				ret+='(';
				ret+=ch;
			}
			else if(ch=='[')
			{
				ret+=ch;
				ret+=']';
			}
			else
			{
				ret+='[';
				ret+=ch;
			}
		}
	}
	cout<<ret;
	return 0;
}