此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本周为第四课的第一周内容,这一课所有内容的中心只有一个:计算机视觉 。应用在深度学习里,就是专门用来进行图学习的模型和技术,是在之前全连接基础上的"特化",也是相关专业里的一个重要研究大类。
这一整节课都存在大量需要反复理解的内容和机器学习、数学基础。 因此我会尽可能的补足基础,用比喻和实例来演示每个部分,从而帮助理解。
本篇的内容关于卷积参数,就像全连接层有很多参数一样,卷积也有很多可以调整的地方。
1. Padding
Padding 的中文可以翻译为"填充",但实际在学术和技术讨论中,大部分人更习惯于使用英文原词,尤其是在编程和文献中,"Padding"已经成为一个标准术语。
在正式介绍 Padding 前,我们先对卷积中的一些基本参数进行符号说明,好方便之后使用。
1.1 卷积的基本符号表示
来看一下卷积中的一些基本表示:
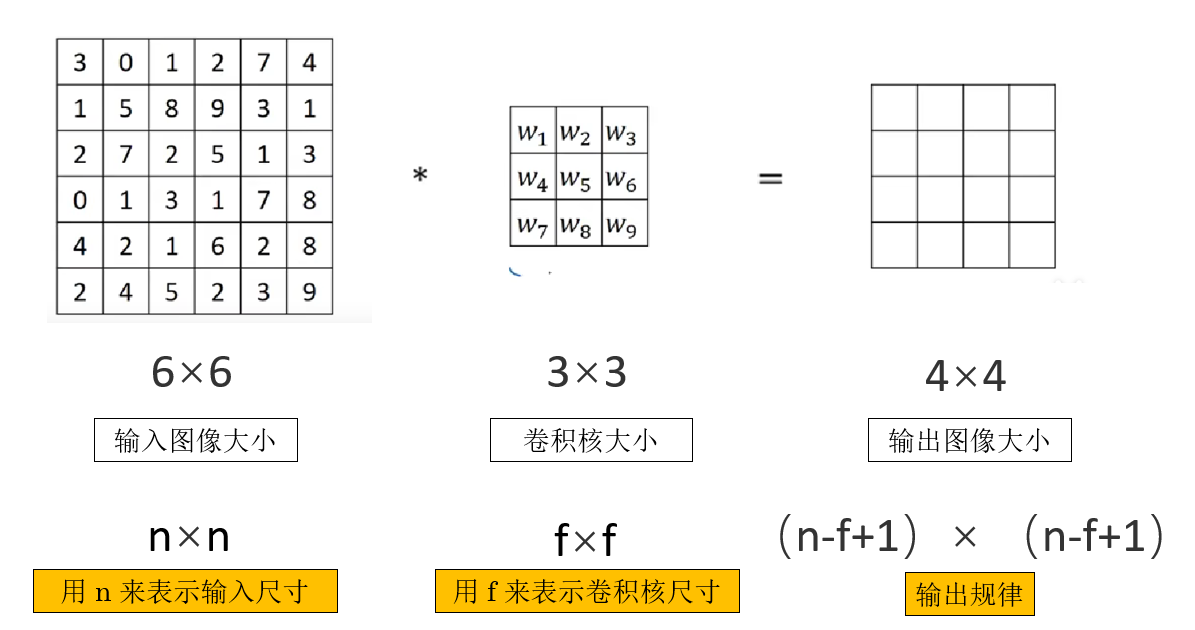
如图所示,再简单列举一下:
- \(n\) 表示输入特征图的空间尺寸(通常指宽或高)。
- \(f\) 表示卷积核的尺寸(同样指宽或高)。
而经过一层最基本的卷积操作,我们可以发现输出图像的尺寸可以表示为:
\[n-f+1 \]
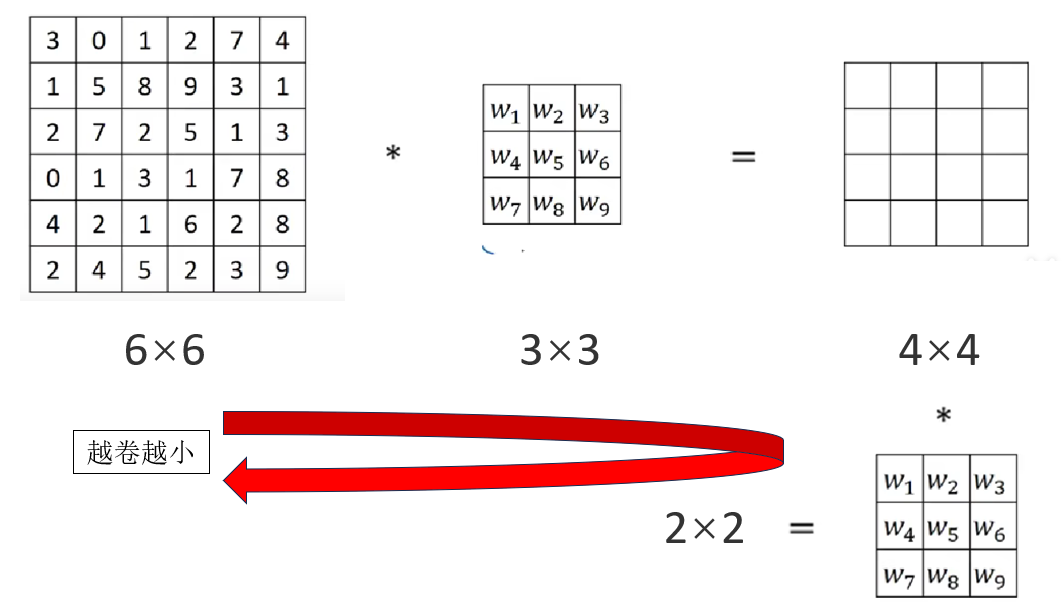
但是这样就会出现一个问题:我们通过卷积核来提取特征,会让图片变小。
就像对一篇文章进行概括,概括一次让 100 个字变成 20 个字,再概括一次就成 5 个字,再概括就只剩下 1 个字了。
一个"好"或者"坏",真的能展示一整篇文章的内容吗?
卷积也是同样的道理,如果不进行处理,那么卷积就会让图片不断变小,信息丢失 。
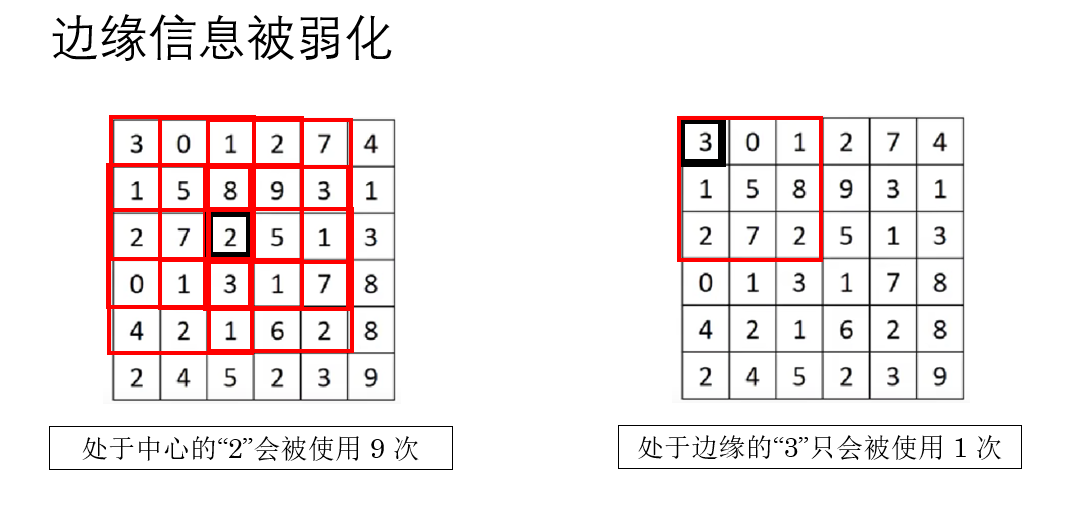
此外,还有一个问题:每个像素的使用不平均,边缘信息被更少的扫描了。
卷积核在滑动时,只能完全覆盖在图像内部的位置 ,边缘那一圈天然"吃亏",被卷积核扫过的次数更少。
如何解决这些问题?答案就是 Padding 。
1.2 什么是 Padding ?
用英文听起来可能有些高大上,但 Padding 的逻辑很简单:既然边缘不够大,那就在四周"垫一点东西"进去。
简单来说:就是围着输入图像再加上一圈或几圈像素。
现在便在引入一个新的符号规范:
我们用 \(p\) 表示 Padding 的大小,用于说明在图像四周填充了多少像素。
而对于用什么填充,也有一些相应的方法:
- 在图像四周增加 0 值像素(称为 zero padding)
- 或者根据某些规则复制原图边缘的像素
我们就用 zero padding 来演示:
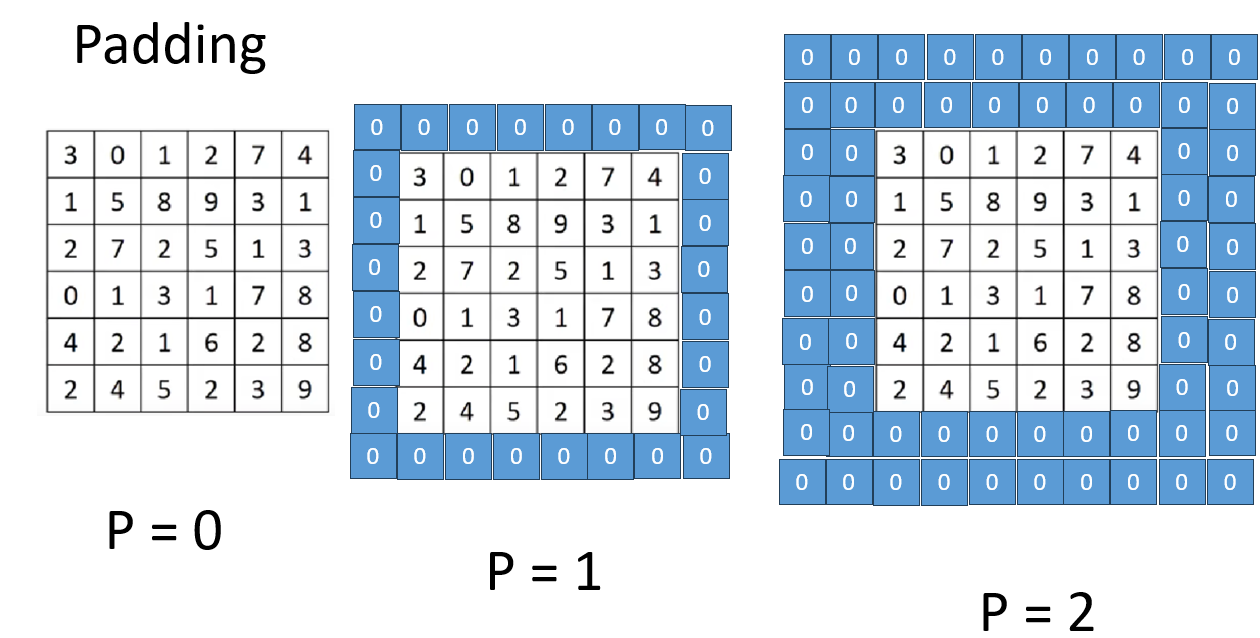
同样,你会发现 \(p\) 的增加有这样的规律:
\[p每增加 1,n 增大 2 \]
因此,在加入 Padding ,我们就会再次更新从输入尺寸到输出尺寸的公式:
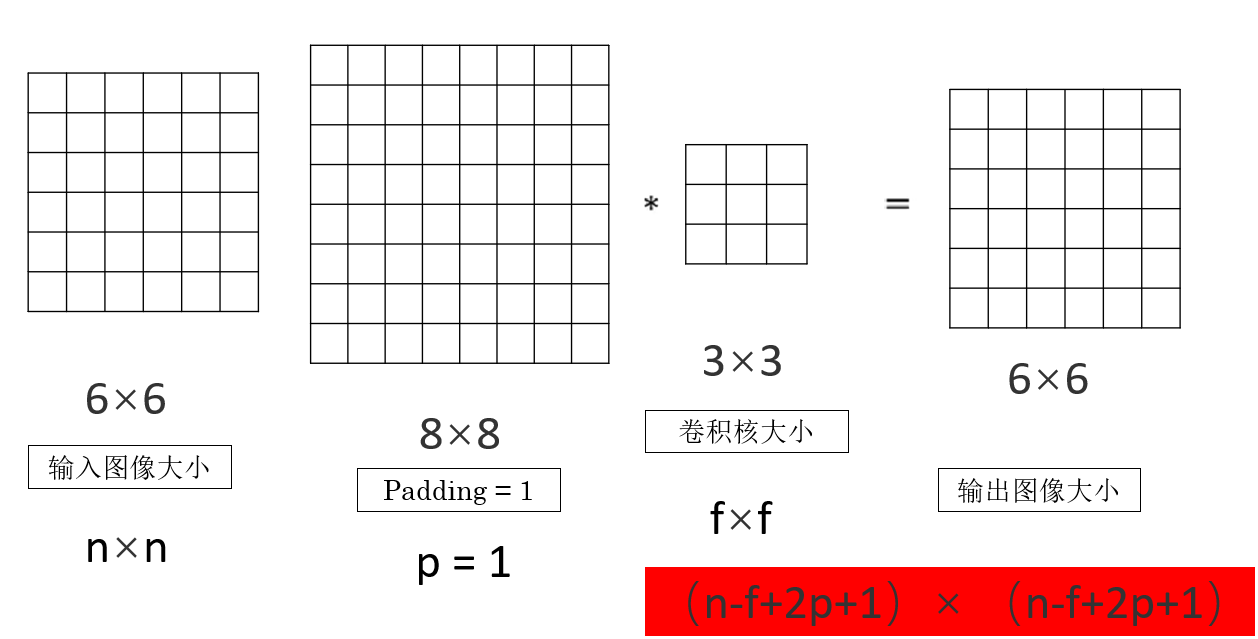
现在,输出图像的一边尺寸就变成了:
\[n-f+2p+1 \]
这样,图片变小和边缘使用少的问题就都会得到改善。
继续下一部分。
1.3 valid 卷积和 same 卷积
这是两种在 Padding 有所区别的卷积方式,简单介绍一下:
(1)valid 卷积(无填充)
"valid" 的字面意思是"有效的"。
对应到我们前面的符号,就是:
\[p = 0 \]
于是输出尺寸就还是:
\[n - f + 1 \]
这类卷积常用于希望逐步压缩空间尺寸、提取更抽象特征的网络结构中。
(2)same 卷积(输出与输入同尺寸)
"same" 的意思是希望输出与输入在空间尺寸上 保持一样大 。
为了维持尺寸不变,我们必须人为加 Padding,让这个公式成立:
\[n - f + 2p + 1 = n \]
整理得到:
\[p = \frac{f - 1}{2} \]
这也是为什么里卷积核常用 奇数尺寸(如 3、5、7) ,因为奇数能让 \(p\) 刚好取整数,否则 same 卷积就无法实现。
same 卷积的意义是:让每一层都在提取特征的同时,不缩小空间尺寸,从而保留更"密集"的空间细节。 这也是我们在卷积网络中普遍选择的卷积方式。
对于 Padding 部分就先到这里,接下来看看另一个参数:步长。
2. 卷积步长(stride)
卷积除了 "卷积核大小" 和 "Padding 要不要填" 外,还有一个非常关键的参数:步长 stride 。如果说卷积核是在"看图",Padding 是在"补图",那 stride 就决定了它"走路的方式"。
简单来说,stride 控制的是:卷积核每次滑动时,移动多少格。
继续引入一个符号规范:
我们用 \(s\) 表示 stride 的大小,用于说明卷积核每次滑动时移动的距离。
之前的内容里,实际上 stride 一直存在,在默认情况下,它的值是:
\[s = 1 \]
意思是:每次往右或往下移动 1 个像素 。
就像你在看一本小说,每翻一页都要翻到紧挨着的下一页,这样你不会漏掉任何内容。
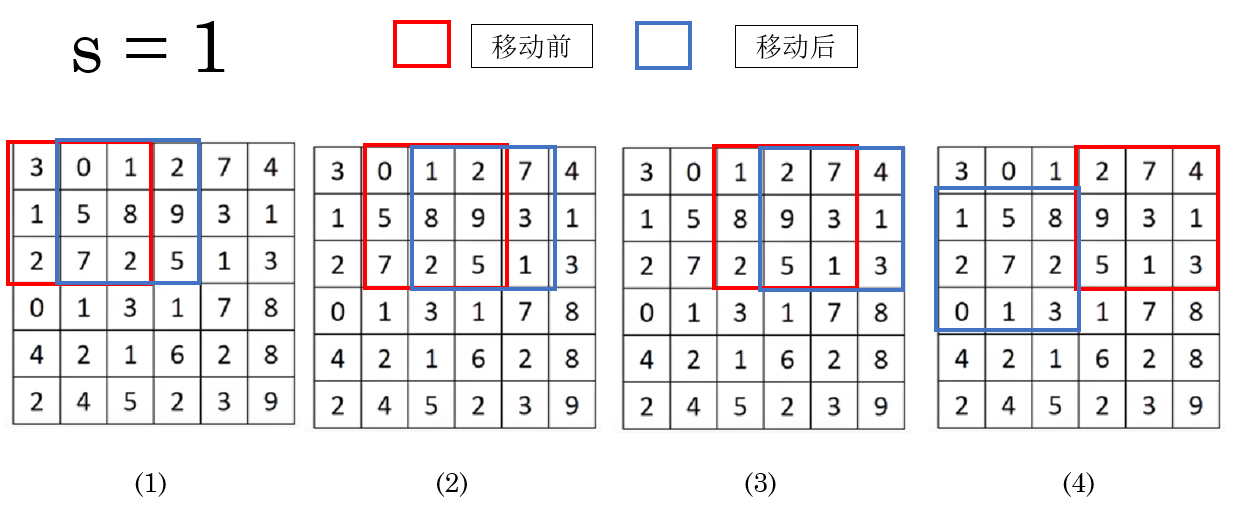
但如果把 stride 调大,比如:
\[s = 2 \]
那就变成每次跳两个格子再看下一块区域。
就像你看画册时,每次跳着翻两页------信息当然会变"稀疏"一些。
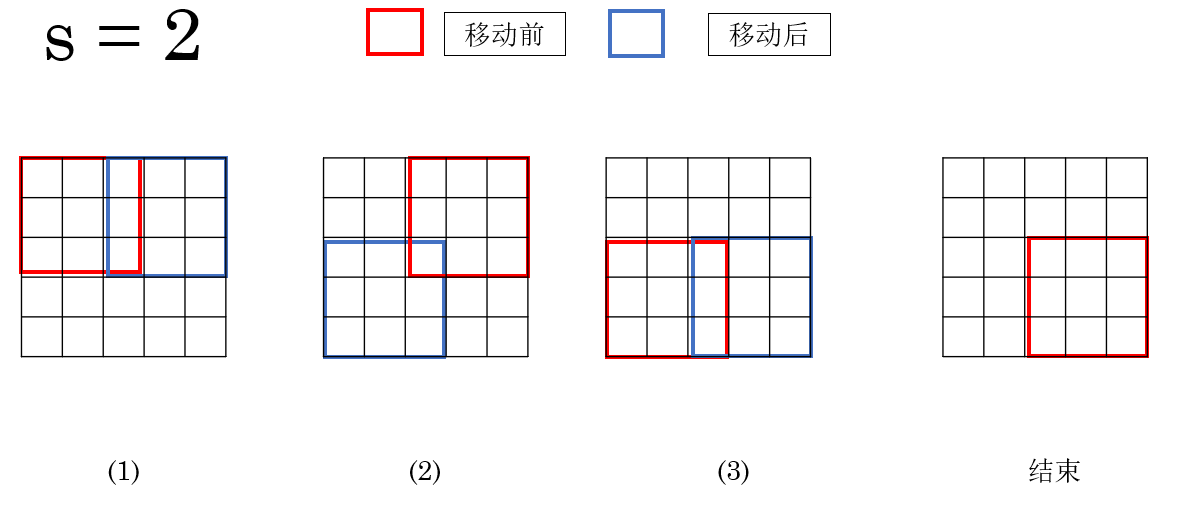
但是当步长增加时,也会出现一种新的情况:
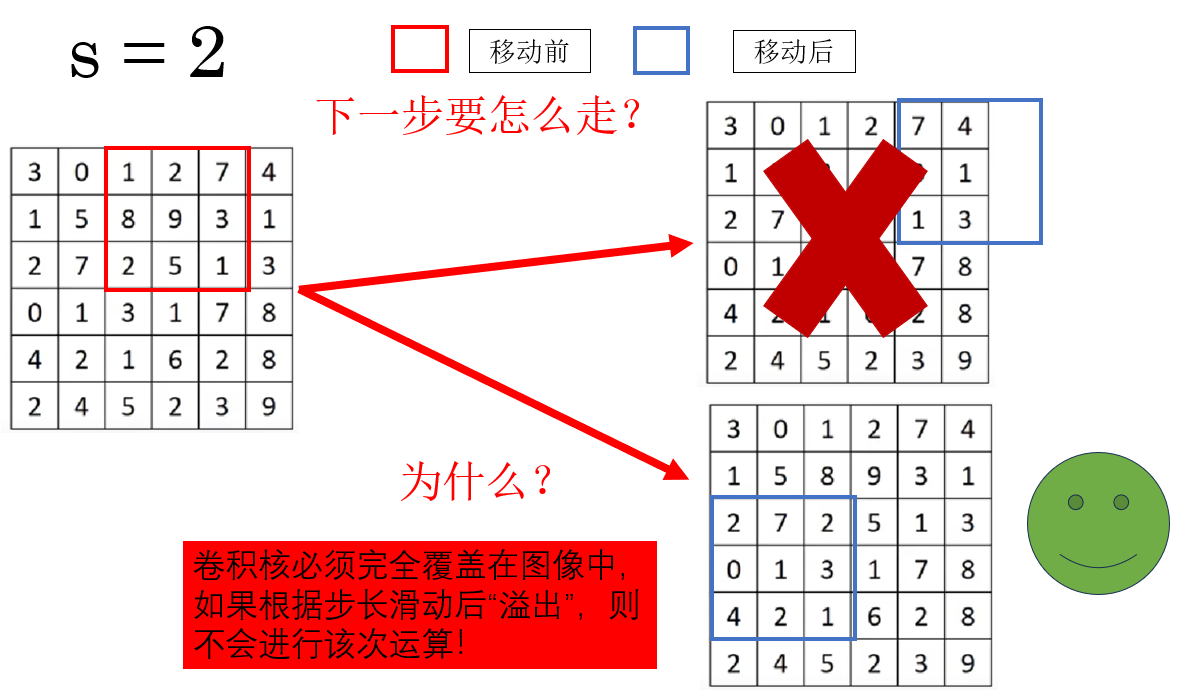
当卷积核有部分移动到图像外时,就不进行该次卷积运算,而是继续滑动至下一个完全覆盖位置或者结束。
实际上,\(s = 1\) 时也是这个逻辑。
因此,这副图像的卷积过程是这样的:
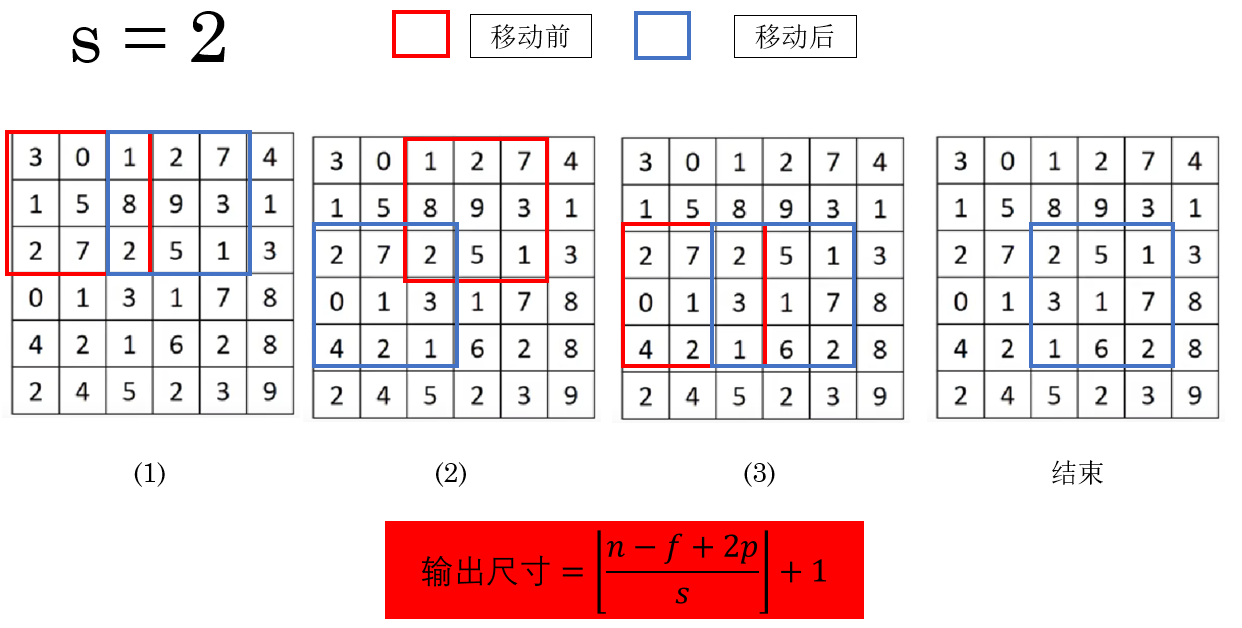
而 stride 的调整也会改变输出特征图的尺寸,输出公式也要随之更新:
\[\text{输出尺寸}=\left\lfloor\frac{n - f + 2p}{s}\right\rfloor + 1, 注:\lfloor向下取整\rfloor \]
同时你会发现,在上图中,如果不进行"溢出"运算,会让一部分像素丢失。
因此,选择 \(f\) 与 \(s\) 时尽量保证输出尺寸为整数,或显式使用 padding 使其对齐。
总结一下:
- s 越大,输出越小,计算量越小,感知范围越大。
- s 越小(最常见是 1),输出保留更密。
这便是卷积的另一个参数:步长 stride。
这一节课程中额外补充了一点:在数学里,卷积并不是上面这样的相乘相加,它在此前会进行一步翻转,我们进行的卷积在数学里叫做互相关。
但是在深度学习里,我们省略了这一步骤,因为我们的卷积核是不断更新的,我们在惯例,在论文里的卷积操作指的就是我们上面所介绍的。了解就好,就不再展开了。
3. 总结
| 概念 | 原理 | 比喻 |
|---|---|---|
| Padding(填充) | 在输入图像四周补上 \(p\) 层像素,使卷积核能在更多位置滑动;解决输出变小、边缘利用不足的问题。输出尺寸公式:\(n-f+2p+1\) | 像给白板贴边框,让贴纸(卷积核)能贴到更靠外的区域,不要让边缘吃亏。 |
| valid 卷积 | 不做填充,\(p=0\),输出会变小:\(n-f+1\) | 像剪纸时只剪"能完整落在纸上的图案",边缘那点不够大的就不要了。 |
| same 卷积 | 通过设置 \(p=\frac{f-1}{2}\) 让输出尺寸保持与输入一样大。必须使用奇数卷积核尺寸。 | 像在桌面四周加垫子,让桌布(卷积结果)铺好后刚好和原桌面一样大。 |
| stride(步长) | 卷积核每次移动的距离,用 \(s\) 表示。决定卷积核的扫描密度。输出尺寸公式:\(\left\lfloor\frac{n-f+2p}{s}\right\rfloor+1\) | s=1 是逐格检查;s=2 是"隔一个扫一个",像翻相册时跳着看。 |
| stride 与信息保留 | s 越大,输出越小、计算更省,但特征更稀疏;s 越小,信息保留越多。 | 像在地上画方块跳格子:跳得越大,踩到的格子越少。 |
| 为什么卷积要向下取整 | 卷积核必须完全落在图像内才能计算,溢出部分不做卷积,因此输出尺寸要取 \(\lfloor\cdot\rfloor\)。 | 像在桌子上摆杯垫,必须完全落在桌面上才能放,否则就算不进去。 |
| 卷积 vs 数学卷积 | 数学中的卷积会翻转核,但深度学习里省略这步,直接做"互相关",因为核会被训练。 | 像做饭时直接根据口味调整调料,不一定非要照传统食谱翻锅步骤。 |