深度学习实战（基于pytroch）系列（四十八）AdaGrad优化算法

AdaGrad优化算法

算法原理

在传统优化方法中，目标函数自变量的所有元素在相同时间步使用统一的学习率进行更新。例如对于二维向量 [ x 1 , x 2 ] ⊤ [x_1, x_2]^\top [x1,x2]⊤，在梯度下降中两个元素都使用相同的学习率 η \eta η：

x 1 ← x 1 − η ∂ f ∂ x 1 , x 2 ← x 2 − η ∂ f ∂ x 2 x_1 \leftarrow x_1 - \eta \frac{\partial f}{\partial x_1}, \quad x_2 \leftarrow x_2 - \eta \frac{\partial f}{\partial x_2} x1←x1−η∂x1∂f,x2←x2−η∂x2∂f

当不同维度的梯度值差异显著时，统一的学习率难以同时满足所有维度的需求：过小的学习率会导致梯度较小维度收敛缓慢，而过大的学习率又会使梯度较大维度发散。

AdaGrad算法通过为每个参数维度自适应调整学习率来解决这一问题。该算法维护一个按元素平方的梯度累加变量 s t \boldsymbol{s}_t st，使得每个参数拥有独立的学习率。

算法流程

AdaGrad算法在时间步0初始化 s 0 \boldsymbol{s}_0 s0 为全零向量。在时间步 t t t：

累积平方梯度 ：
s t ← s t − 1 + g t ⊙ g t \boldsymbol{s}t \leftarrow \boldsymbol{s}{t-1} + \boldsymbol{g}_t \odot \boldsymbol{g}_t st←st−1+gt⊙gt

其中 ⊙ \odot ⊙ 表示按元素相乘， g t \boldsymbol{g}_t gt 是小批量随机梯度。
参数更新 ：
x t ← x t − 1 − η s t + ϵ ⊙ g t \boldsymbol{x}t \leftarrow \boldsymbol{x}{t-1} - \frac{\eta}{\sqrt{\boldsymbol{s}_t + \epsilon}} \odot \boldsymbol{g}_t xt←xt−1−st+ϵ η⊙gt

其中 η \eta η 是基础学习率， ϵ \epsilon ϵ 是为保证数值稳定性添加的小常数（如 1 0 − 6 10^{-6} 10−6）。

算法特性

自适应学习率 ：梯度较大的参数对应较小的有效学习率，梯度较小的参数对应较大的有效学习率
单调递减 ：由于 s t \boldsymbol{s}_t st 持续累积平方梯度，所有参数的学习率在训练过程中单调递减
潜在问题：在训练后期，学习率可能过小导致收敛困难

算法演示

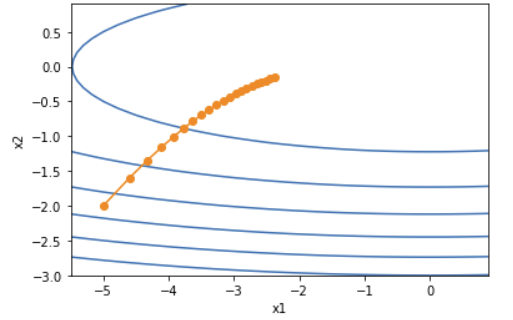
我们以目标函数 f ( x ) = 0.1 x 1 2 + 2 x 2 2 f(\boldsymbol{x}) = 0.1x_1^2 + 2x_2^2 f(x)=0.1x12+2x22 为例，展示AdaGrad的优化过程。

PyTorch实现

python 复制代码

%matplotlib inline
import torch
import math
import matplotlib.pyplot as plt

def adagrad_2d(x1, x2, s1, s2, eta=0.4):
    """AdaGrad算法在二维目标函数上的应用"""
    g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6  # 计算梯度
    s1 += g1 ** 2
    s2 += g2 ** 2
    x1 -= eta / math.sqrt(s1 + eps) * g1
    x2 -= eta / math.sqrt(s2 + eps) * g2
    return x1, x2, s1, s2

def f_2d(x1, x2):
    """二维目标函数"""
    return 0.1 * x1 ** 2 + 2 * x2 ** 2

def train_2d(trainer, steps=20):
    """训练过程"""
    x1, x2 = -5, -2
    s1, s2 = 0, 0
    results = [(x1, x2)]
    for i in range(steps):
        x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
        results.append((x1, x2))
        print(f'epoch {i+1}, x1 {x1:.6f}, x2 {x2:.6f}')
    return results

def show_trace_2d(f, results):
    """可视化优化轨迹"""
    plt.figure(figsize=(6, 4))
    x1, x2 = zip(*results)
    plt.plot(x1, x2, '-o', color='#ff7f0e')
    
    # 绘制等高线
    x1 = torch.arange(-5.5, 1.0, 0.1)
    x2 = torch.arange(-3.0, 1.0, 0.1)
    X1, X2 = torch.meshgrid(x1, x2, indexing='ij')
    Z = f(X1, X2)
    plt.contour(X1, X2, Z, colors='#1f77b4')
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.show()

# 测试不同学习率的效果
print("学习率 = 0.4:")
results = train_2d(adagrad_2d)
show_trace_2d(f_2d, results)

输出

学习率 = 0.4:

epoch 1, x1 -4.600000, x2 -1.600000

epoch 2, x1 -4.329178, x2 -1.350122

epoch 3, x1 -4.114228, x2 -1.163597

epoch 4, x1 -3.932302, x2 -1.014436

epoch 5, x1 -3.772835, x2 -0.890767

epoch 6, x1 -3.629933, x2 -0.785968

epoch 7, x1 -3.499909, x2 -0.695875

epoch 8, x1 -3.380281, x2 -0.617648

epoch 9, x1 -3.269280, x2 -0.549239

epoch 10, x1 -3.165593, x2 -0.489098

epoch 11, x1 -3.068216, x2 -0.436016

epoch 12, x1 -2.976356, x2 -0.389023

epoch 13, x1 -2.889378, x2 -0.347323

epoch 14, x1 -2.806763, x2 -0.310253

epoch 15, x1 -2.728078, x2 -0.277253

epoch 16, x1 -2.652960, x2 -0.247842

epoch 17, x1 -2.581099, x2 -0.221608

epoch 18, x1 -2.512228, x2 -0.198191

epoch 19, x1 -2.446117, x2 -0.177277

epoch 20, x1 -2.382563, x2 -0.158591

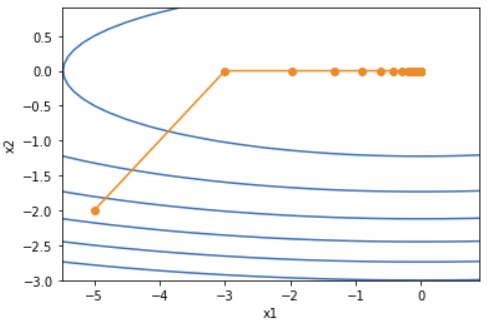
下面将学习率增大到2。可以看到自变量更为迅速地逼近了最优解。

python 复制代码

print("\n学习率 = 2:")
results = train_2d(lambda x1, x2, s1, s2: adagrad_2d(x1, x2, s1, s2, eta=2))
show_trace_2d(f_2d, results)

输出

epoch 1, x1 -3.000001, x2 -0.000000

epoch 2, x1 -1.971010, x2 -0.000000

epoch 3, x1 -1.330559, x2 -0.000000

epoch 4, x1 -0.907975, x2 -0.000000

epoch 5, x1 -0.622554, x2 -0.000000

epoch 6, x1 -0.427785, x2 -0.000000

epoch 7, x1 -0.294250, x2 -0.000000

epoch 8, x1 -0.202494, x2 -0.000000

epoch 9, x1 -0.139383, x2 -0.000000

epoch 10, x1 -0.095951, x2 -0.000000

epoch 11, x1 -0.066056, x2 -0.000000

epoch 12, x1 -0.045477, x2 -0.000000

epoch 13, x1 -0.031309, x2 -0.000000

epoch 14, x1 -0.021555, x2 -0.000000

epoch 15, x1 -0.014840, x2 -0.000000

epoch 16, x1 -0.010217, x2 -0.000000

epoch 17, x1 -0.007034, x2 -0.000000

epoch 18, x1 -0.004843, x2 -0.000000

epoch 19, x1 -0.003334, x2 -0.000000

epoch 20, x1 -0.002295, x2 -0.000000

完整实现

从零开始实现

代码中的s_w：对应权重参数 w \boldsymbol{w} w 的累加变量 s t w \boldsymbol{s}_t^w stw

代码中的s_b：对应偏置参数 b \boldsymbol{b} b 的累加变量 s t b \boldsymbol{s}_t^b stb

python 复制代码

import torch
import torch.utils.data as Data
from torch import nn, optim
import numpy as np
import matplotlib.pyplot as plt
import time

# 生成模拟数据
def get_data_ch7():  
    data = np.genfromtxt('../data/airfoil_self_noise.dat', delimiter='\t')
    data = (data - data.mean(axis=0)) / data.std(axis=0)
    return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
           torch.tensor(data[:1500, -1], dtype=torch.float32)



def init_adagrad_states(features):
    """初始化AdaGrad状态变量"""
    s_w = torch.zeros((features.shape[1], 1))
    s_b = torch.zeros(1)
    return (s_w, s_b)

def adagrad(params, states, hyperparams):
    """AdaGrad更新规则"""
    eps = 1e-6
    for p, s in zip(params, states):
        with torch.no_grad():
            # 累积平方梯度
            s[:] += (p.grad ** 2)
            # 参数更新
            p[:] -= hyperparams['lr'] * p.grad / torch.sqrt(s + eps)
        p.grad.data.zero_()

def train_ch7(trainer_fn, states, hyperparams, features, labels,
              batch_size=10, num_epochs=2):
    # 初始化模型
    net, loss = linreg, squared_loss
    w = torch.normal(mean=0, std=0.01, size=(features.shape[1], 1), 
                     dtype=torch.float32, requires_grad=True)
    b = torch.zeros(1, dtype=torch.float32, requires_grad=True)

    def eval_loss():
        return loss(net(features, w, b), labels).mean().item()

    ls = [eval_loss()]
    data_iter = Data.DataLoader(
        Data.TensorDataset(features, labels), batch_size, shuffle=True)
    
    for _ in range(num_epochs):
        start = time.time()
        for batch_i, (X, y) in enumerate(data_iter):
            l = loss(net(X, w, b), y).mean()  # 使用平均损失
            l.backward()
            trainer_fn([w, b], states, hyperparams)  # 迭代模型参数
            # 梯度清零
            w.grad.data.zero_()
            b.grad.data.zero_()
            if (batch_i + 1) * batch_size % 100 == 0:
                ls.append(eval_loss())  # 每100个样本记录下当前训练误差
    # 打印结果和作图
    print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
    plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
    plt.xlabel('epoch')
    plt.ylabel('loss')
    plt.show()

# 线性回归模型
def linreg(X, w, b):
    return torch.mm(X, w) + b

# 平方损失
def squared_loss(y_hat, y):
    return (y_hat - y.view(y_hat.size())) ** 2 / 2

我们用0.1的学习率来训练模型

python 复制代码

train_ch7(adagrad, init_adagrad_states(features), {'lr': 0.1}, features, labels)

使用PyTorch内置优化器

python 复制代码

def train_pytorch_ch7(optimizer_fn, optimizer_hyperparams, features, labels,
                    batch_size=10, num_epochs=2):
    # 初始化模型
    net = nn.Sequential(
        nn.Linear(features.shape[-1], 1)
    )
    loss = nn.MSELoss()
    optimizer = optimizer_fn(net.parameters(), **optimizer_hyperparams)

    def eval_loss():
        return loss(net(features).view(-1), labels).item() / 2

    ls = [eval_loss()]
    data_iter = torch.utils.data.DataLoader(
        torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)

    for _ in range(num_epochs):
        start = time.time()
        for batch_i, (X, y) in enumerate(data_iter):
            l = loss(net(X).view(-1), y) / 2
            
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            if (batch_i + 1) * batch_size % 100 == 0:
                ls.append(eval_loss())
    # 打印结果和作图
    print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
    plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
    plt.xlabel('epoch')
    plt.ylabel('loss')
    plt.show()

train_pytorch_ch7(optim.Adagrad, {'lr': 0.1}, features, labels)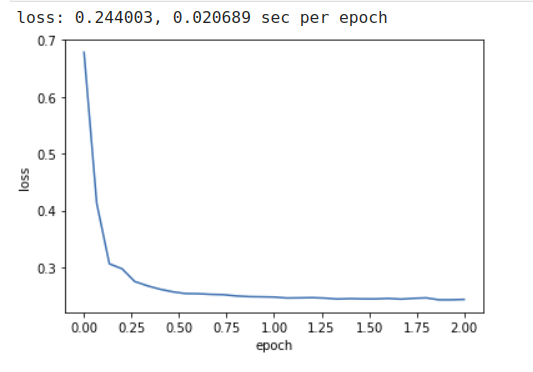

算法总结

核心思想：AdaGrad通过为每个参数维护独立的学习率，根据历史梯度信息自适应调整更新幅度
优势：
- 自动适应不同参数的梯度尺度
- 减少手动调整学习率的负担
- 对稀疏梯度场景表现良好
局限性 ：
- 学习率单调递减可能导致后期训练停滞
- 累积平方梯度可能使学习率过早变得过小

AdaGrad算法特别适用于处理稀疏数据和特征尺度差异较大的优化问题，为后续自适应优化算法（如RMSProp、Adam）的发展奠定了基础。

本系列目录链接