2025年第七届全国高校计算机能力挑战赛 决赛 Java组 编程题汇总

核心总结

B类Lyndon字符串分解 样例存在错误 ，详情见 [B题勘误]

编程题共5个大类，每类含2道变种
A类螺旋矩阵遍历 与C类数据校准 为偏易，分别聚焦模拟遍历与差分贪心逻辑，侧重基础流程控制与算法应用；
B类Lyndon字符串分解 与E类实时中位数 难度中等，核心分别是双指针贪心与双堆维护，需掌握关键数据结构与贪心策略；
D类灯带问题 综合状态压缩与矩阵快速幂，涉及大规模数据优化，难度中等偏上。

整体适配算法入门至进阶阶段学习者

文章目录

• 核心总结
• A-螺旋矩阵遍历问题
• • A1-初始方向右，矩阵形式输出
  • A2-初始方向右，展平序列输出
• B-Lyndon字符串分解问题
• B题勘误
• • B1-仅输出右端点的异或和
  • B2-输出右端点及异或和
• C-数据校准/服务器调整问题
• • C1-设备读数分n行输入
  • C2-设备读数一行输入
• D-灯带/灯珠问题
• • D1-灯带为环形（首尾相邻）
  • D2-灯带为直线形（首尾不相邻）
• E-实时中位数问题
• • E1-仅输出每次录入后的实时中位数
  • E2-输出实时中位数及最终平均值

A-螺旋矩阵遍历问题

相似题目差异总结：

• 核心差异：输出格式不同（矩阵形式/展平序列）、初始方向不同（右/左）；核心区别聚焦输出形态。
• 核心算法：一致采用「从中心出发，按顺时针旋转规则遍历，记录顺序编号」的模拟策略，通过方向数组控制移动，二维数组标记已访问状态。
• 优化点：使用Arrays.fill初始化标记数组，边界判断提前终止循环，StringBuilder拼接输出结果，避免n=1e3时的IO冗余和内存浪费。

A1-初始方向右，矩阵形式输出

题目描述 ：在遥远的魔法王国，有一个神秘的迷宫，由大小为n×n的方格组成。勇者小明被困在迷宫的中央，他必须点亮迷宫的每一个方格才能找到出口。迷宫的规律十分奇特，而这个规律就是旋螺线！小明初始方向为（→），即先向前走一步。接下来他总是优先选择现在所在方向右侧未被点亮的方格，如果右边有可走的方格，他会顺时针旋转90°并继续前进。（即假设现在方向为→且→的右方未被走，→变为↓）小明每点亮一个方格，就记录该方格的顺序编号，从0开始计数。迷宫的中心位置：对于奇数边长的迷宫，中心为 ( n + 1 2 , n + 1 2 ) (\frac{n+1}{2},\frac{n+1}{2}) (2n+1,2n+1)；对于偶数边长的迷宫，中心为 ( n 2 , n 2 ) (\frac{n}{2},\frac{n}{2}) (2n,2n)。你的任务是输出迷宫中每个方格被点亮的顺序编号。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 第一行输入一个整数n，表示迷宫的边长。

输出格式：

• 输出n×n个整数，每行输出一行矩阵对应的编号，用空格分隔。
• 编号从0开始，表示每个方格被点亮的顺序。

输入输出样例：

• 样例1：
  输入 ：

  1

  输出 ：

  0

• 样例2：
  输入 ：

  2

  输出 ：

  0 1
  3 2

修改后代码：

import java.io.*;
import java.util.*;

public class Main {
    // 方向数组：右(1,0)、下(0,1)、左(-1,0)、上(0,-1)（顺时针顺序，初始方向为右）
    private static final int[][] DIRECTIONS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String inputLine = br.readLine();
        if (inputLine == null || inputLine.trim().isEmpty()) {
            br.close();
            return;
        }
        int n = Integer.parseInt(inputLine.trim());
        br.close();

        // 初始化迷宫矩阵，-1表示未点亮
        int[][] matrix = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(matrix[i], -1);
        }

        // 计算中心坐标
        int centerRow = (n % 2 == 1) ? n / 2 : (n / 2) - 1;
        int centerCol = centerRow;

        // 执行螺旋填充（核心逻辑与原始代码一致，仅优化结构和变量名）
        fillSpiralFromCenter(matrix, n, centerRow, centerCol);

        // 拼接并输出结果
        StringBuilder resultSb = new StringBuilder();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (j > 0) {
                    resultSb.append(' ');
                }
                resultSb.append(matrix[i][j]);
            }
            if (i + 1 < n) {
                resultSb.append('\n');
            }
        }
        System.out.print(resultSb.toString());
    }

    /**
     * 从中心开始按规则填充螺旋矩阵
     * @param matrix 待填充矩阵
     * @param n 矩阵边长
     * @param centerRow 中心行坐标
     * @param centerCol 中心列坐标
     */
    private static void fillSpiralFromCenter(int[][] matrix, int n, int centerRow, int centerCol) {
        int totalCells = n * n;
        int filledCount = 0; // 已点亮的方格数
        int currentNum = 0;  // 当前要记录的编号
        int dirIndex = 0;    // 当前方向索引（0-右，1-下，2-左，3-上）
        int stepLen = 1;     // 每次前进的步数
        int currX = 0;       // 相对于中心的X偏移（对应原始x）
        int currY = 0;       // 相对于中心的Y偏移（对应原始y）

        // 填充逻辑与原始代码完全一致，仅替换变量名提升可读性
        while (filledCount < totalCells) {
            // 每个方向组前进2次
            for (int loop = 0; loop < 2; loop++) {
                int dx = DIRECTIONS[dirIndex][0];
                int dy = DIRECTIONS[dirIndex][1];

                // 按当前步长前进
                for (int step = 0; step < stepLen; step++) {
                    // 计算实际坐标（原始rr = r0 + y，cc = c0 + x 的等价转换）
                    int realRow = centerRow + currY;
                    int realCol = centerCol + currX;

                    // 验证坐标合法且未被点亮
                    if (realRow >= 0 && realRow < n && realCol >= 0 && realCol < n && matrix[realRow][realCol] == -1) {
                        matrix[realRow][realCol] = currentNum;
                        filledCount++;
                        currentNum++;
                        // 填满所有方格后直接返回（替代原始outer标签）
                        if (filledCount == totalCells) {
                            return;
                        }
                    }

                    // 移动到下一个偏移位置
                    currX += dx;
                    currY += dy;
                }

                // 顺时针旋转方向（与原始di = (di + 1) & 3 逻辑一致）
                dirIndex = (dirIndex + 1) % 4;
            }

            // 每完成2次方向前进，步长+1
            stepLen++;
        }
    }
}

A2-初始方向右，展平序列输出

题目描述：在群星陨落之后，世界陷入了无尽的黑夜。传说，在世界的尽头，有一座漂浮在虚空中的星陨方阵------那是诸神留下的最后一座灯塔。它由无数闪烁着残余星辉的魔法方格构成，排列成n×n的神秘阵列。年轻的星行者·小明，为了重启这座灯塔，踏入了方阵的中央。他必须让每一块方格重新点亮，唤醒沉睡的星光。方阵的法则早已被古老的星文铭刻：小明初始方向为（→），先向前进一步。接下来的每一步，如果右侧尚未点亮的方格，他都会顺时针旋转90°并继续前进，呈现出美丽的旋螺线形状。（即假设现在方向为→且→的右方未被点亮，则→变为↓）每当他点亮一块方格，就会在上面留下一个顺序编号，从0开始计数，象征星光重生的次序。方阵的中心坐标为：若n为奇数：((n+1)/2, (n+1)/2)；若n为偶数：(n/2, n/2)。你的任务是：重现这场"星光复苏"的过程，输出每个方格被点亮的顺序编号。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 第一行输入一个整数n，表示方阵的边长。

输出格式：

• 输出n×n个整数，输出一行矩阵对应行的编号，用空格分隔。
• 编号从0开始，表示每个方格被点亮的顺序。

输入输出样例：

• 样例1：
  输入 ：

  2

  输出 ：

  0 1 3 2

• 样例2：
  输入 ：

  3

  输出 ：

  6 7 8 5 0 1 4 3 2

修改后代码：

import java.io.*;
import java.util.*;

public class Main {
    static class InputReader {
        private InputStream in;
        private byte[] buffer = new byte[1 << 16];
        private int ptr = 0;
        private int bufferLen = 0;

        public InputReader(InputStream in) {
            this.in = in;
        }

        public int readInt() throws IOException {
            int c;
            // 跳过空白字符
            do {
                c = readByte();
                if (c == -1) return -1;
            } while (c <= ' ');

            int sign = 1;
            if (c == '-') {
                sign = -1;
                c = readByte();
            }

            int value = 0;
            while (c > ' ') {
                value = value * 10 + (c - '0');
                c = readByte();
            }
            return value * sign;
        }

        private int readByte() throws IOException {
            if (ptr >= bufferLen) {
                bufferLen = in.read(buffer);
                ptr = 0;
                if (bufferLen <= 0) return -1;
            }
            return buffer[ptr++];
        }
    }

    public static void main(String[] args) throws Exception {
        InputReader reader = new InputReader(System.in);
        int n = reader.readInt();
        int totalCells = n * n;
        int[][] matrix = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(matrix[i], -1);
        }

        // 方向数组：上、右、下、左（顺时针旋转顺序）
        int[] dirX = {-1, 0, 1, 0};
        int[] dirY = {0, 1, 0, -1};
        int currDir = 0; // 初始方向：右（对应dirX[1], dirY[1]）
        int currX, currY;

        // 计算中心坐标
        if (n % 2 == 1) {
            currX = currY = n / 2;
        } else {
            currX = currY = (n / 2) - 1;
        }

        // 点亮中心方格
        matrix[currX][currY] = 0;
        // 遍历剩余方格
        for (int num = 1; num < totalCells; num++) {
            // 尝试顺时针旋转90°后的新方向
            int newDir = (currDir + 1) % 4;
            int nextX = currX + dirX[newDir];
            int nextY = currY + dirY[newDir];

            // 新方向可走则切换方向
            if (isValid(nextX, nextY, n) && matrix[nextX][nextY] == -1) {
                currDir = newDir;
            }

            // 移动到下一个方格并点亮
            currX += dirX[currDir];
            currY += dirY[currDir];
            matrix[currX][currY] = num;
        }

        // 展平矩阵为一行输出
        StringBuilder resultSb = new StringBuilder();
        boolean isFirst = true;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (!isFirst) {
                    resultSb.append(' ');
                }
                resultSb.append(matrix[i][j]);
                isFirst = false;
            }
        }
        System.out.print(resultSb.toString());
    }

    // 检查坐标是否在方阵内
    private static boolean isValid(int x, int y, int n) {
        return x >= 0 && x < n && y >= 0 && y < n;
    }
}

B-Lyndon字符串分解问题

B题勘误

两道变种题均是同样的错误

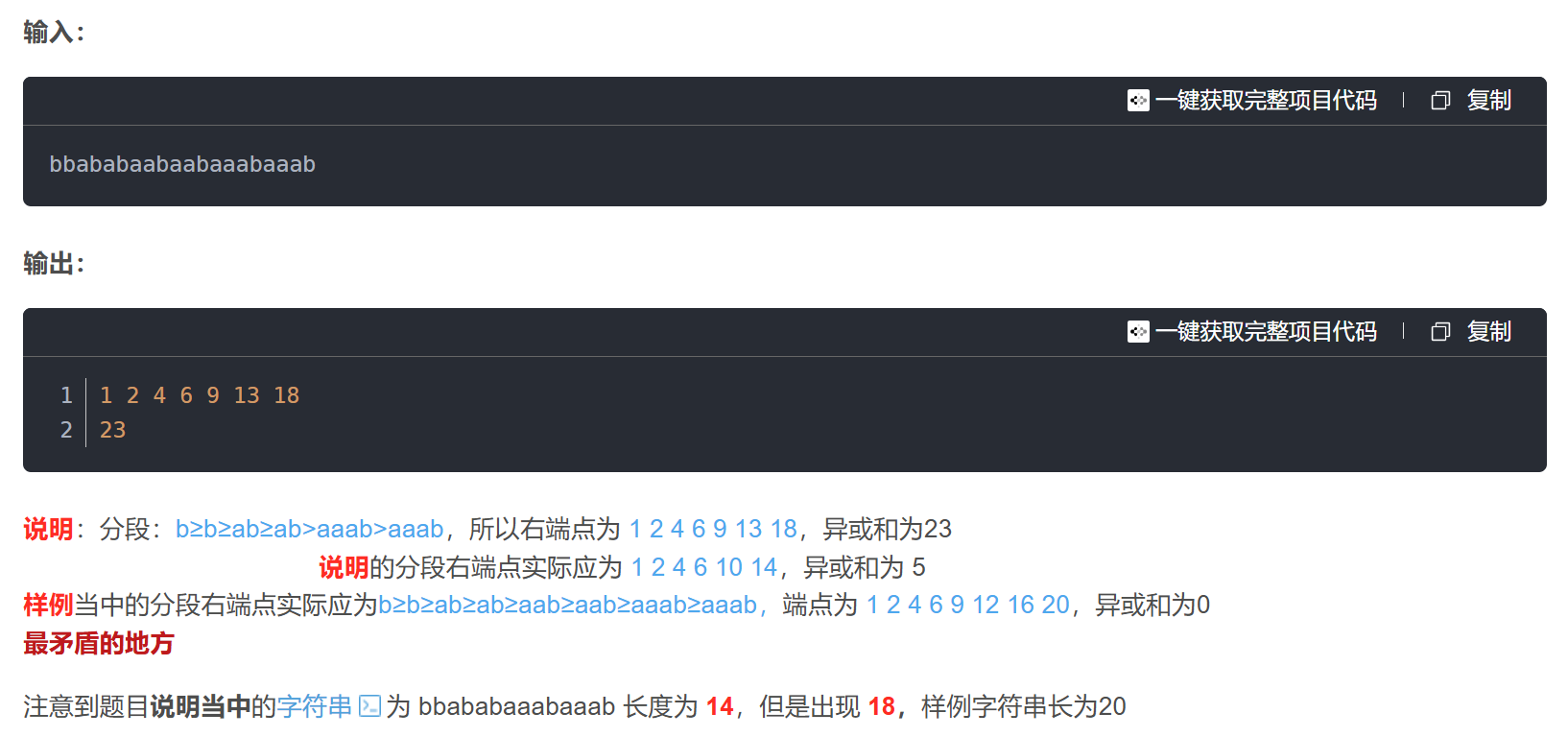
简化题目意思，不考虑任何实现就是

分割字符串，将所有右端点下标值 异或和就是最终结果

因为第二个样例字符串长度是 20 ，最后一个右端点应该是20，样例最后一个端点是 18 ，并且解释分段的字符数量只有 14 ，三重矛盾

相似题目差异总结：

• 核心差异：输出要求不同（仅异或和/端点+异或和），B3与B1输出要求一致且重复；前两题核心区别在于是否需要输出具体右端点，B2需额外拼接端点字符串并控制内存。
• 核心算法：一致采用「基于Lyndon串性质的贪心分解」策略，通过双指针（i、j、k）找到最长Lyndon子串，确保分段满足非递增要求。
• 优化点：使用BufferedInputStream快速读取输入字符串，避免String频繁拼接，B2中通过分批输出端点字符串（超过1<<20时即时打印），适配n=5e6+1的大数据量。

B1-仅输出右端点的异或和

题目描述：在奇幻王国里，有一种神秘的魔法符文------Lyndon符文。每个符文都是由小写字母组成的字符串，而它们的魔力来源于字典序最小的属性：一个符文是Lyndon符文当且仅当它在所有可能的后缀中是最"轻"的（字典序最小）。国王想要对王国的魔法阵进行分段布置，以确保魔法力量最大化。魔法阵是一个由字母组成的长串s，他希望将它分成若干段：s = s₁s₂s₃⋯sₘ。分段要求如下：每段sᵢ都必须是Lyndon符文；魔力递减：每段的字典序必须满足非递增，即s₁≥s₂≥⋯≥sₘ。国王并不关心每段的内容，他只想知道每段右端点的位置（位置从1开始编号）。为了便于记录，他要求你输出这些右端点的异或和，这样只用一个数就能验证魔法阵是否正确分段。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 一行，包含一个长度为n的仅由小写字母组成的字符串s。

输出格式：

• 一个整数，表示所有右端点的异或和。

输入输出样例：

• 样例1：
  输入 ：

  ababa

  输出 ：

  3

  说明：答案为2 4 5，异或后为3

• 样例2：
  输入 ：

  bbababaabaabaaabaaab

  输出 ：

  23

  说明：答案为1 2 4 6 9 13 18，异或后和为23

修改后代码：

import java.io.*;

public class Main {
    public static void main(String[] args) throws Exception {
        // 快速读取输入字符串
        BufferedInputStream inputStream = new BufferedInputStream(System.in);
        StringBuilder strSb = new StringBuilder();
        int charCode;
        while ((charCode = inputStream.read()) != -1) {
            // 跳过换行和回车
            if (charCode == '\n' || charCode == '\r') {
                break;
            }
            strSb.append((char) charCode);
        }
        char[] charArr = strSb.toString().toCharArray();
        int strLen = charArr.length;

        int start = 0; // 当前分段起始位置（0-based）
        int xorSum = 0; // 右端点异或和
        int currentEnd = 0; // 当前分段右端点（1-based）

        while (start < strLen) {
            int next = start + 1; // 下一个字符位置
            int current = start; // 当前比较指针

            // 寻找最长Lyndon子串的边界
            while (next < strLen && charArr[current] <= charArr[next]) {
                if (charArr[current] < charArr[next]) {
                    // 发现更小后缀，重置current到起始位置
                    current = start;
                } else {
                    // 字符相等，移动current
                    current++;
                }
                next++;
            }

            // 计算当前Lyndon子串长度
            int subLen = next - current;

            // 划分当前分段（可能包含多个相同Lyndon子串）
            while (start <= current) {
                currentEnd += subLen;
                xorSum ^= currentEnd;
                start += subLen;
            }
        }

        System.out.print(xorSum);
    }
}

B2-输出右端点及异或和

题目描述 ：在遥远的奇幻王国里，流传着一种古老的魔法符文------Lyndon符文。每个符文都是由小写字母组成的字符串，而它们的神秘力量来源于一个特性：在所有可能的后缀中，它是字典序最小的字符串。只有满足这个条件的字符串才能被称为Lyndon符文。国王正在规划一块巨大的魔法阵，他希望将这块魔法阵切分成若干连续区域，每一区域都是一个Lyndon符文段：S = s₁s₂s₃⋯sₘ。为了保证魔法阵的能量层层递减，每一段的字典序必须非递增，即 s 1 ≥ s 2 ≥ ⋯ ≥ s m s_1 \ge s_2 \ge \cdots \ge s_m s1≥s2≥⋯≥sm。国王不需要知道每段具体内容，他只关心每段右端点的位置（从1开始编号）。为了方便记录，他要求输出这些右端点以及右端点的异或和，用一个数字就能验证整个魔法阵是否划分正确。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 一行，包含一个长度为n的仅由小写字母组成的字符串s。

输出格式：

• 第一行输出划分的右端点，用空格隔开。
• 一个整数，表示所有右端点的异或和。

输入输出样例：

• 样例1：
  输入 ：

  ababa

  输出 ：

  2 4 5
  3

  说明：分段：ab≥ab>a，所以右端点为2 4 5，异或和为3

• 样例2：
  输入 ：

  bbababaabaabaaabaaab

  输出 ：

  1 2 4 6 9 13 18
  23

  说明：分段：b≥b≥ab≥ab>aaab>aaab，所以右端点为1 2 4 6 9 13 18，异或和为23

修改后代码：

import java.io.*;

public class Main {
    private static final int BUFFER_THRESHOLD = 1 << 20; // 1MB缓冲阈值

    public static void main(String[] args) throws Exception {
        BufferedInputStream inputStream = new BufferedInputStream(System.in);
        StringBuilder strBuilder = new StringBuilder();
        int byteCode;

        // 读取输入字符串
        while ((byteCode = inputStream.read()) != -1) {
            if (byteCode == '\n' || byteCode == '\r') {
                break;
            }
            strBuilder.append((char) byteCode);
        }

        char[] charArray = strBuilder.toString().toCharArray();
        int strLength = charArray.length;
        int startIdx = 0;
        long xorResult = 0;
        int endPos = 0;
        StringBuilder resultSb = new StringBuilder();
        boolean firstEnd = true;

        while (startIdx < strLength) {
            int nextIdx = startIdx + 1;
            int currPtr = startIdx;

            // 双指针寻找最长Lyndon子串
            while (nextIdx < strLength && charArray[currPtr] <= charArray[nextIdx]) {
                if (charArray[currPtr] < charArray[nextIdx]) {
                    currPtr = startIdx;
                } else {
                    currPtr++;
                }
                nextIdx++;
            }

            int subLength = nextIdx - currPtr;

            // 划分分段并记录右端点
            while (startIdx <= currPtr) {
                endPos += subLength;
                // 拼接右端点（处理空格）
                if (!firstEnd) {
                    resultSb.append(' ');
                }
                resultSb.append(endPos);
                firstEnd = false;
                // 计算异或和
                xorResult ^= endPos;
                // 移动起始位置
                startIdx += subLength;

                // 缓冲超过阈值时即时输出，避免内存溢出
                if (resultSb.length() > BUFFER_THRESHOLD) {
                    System.out.print(resultSb.toString());
                    resultSb.setLength(0);
                }
            }
        }

        // 输出剩余右端点
        System.out.println(resultSb.toString());
        // 输出异或和
        System.out.print(xorResult);
    }
}

C-数据校准/服务器调整问题

相似题目差异总结：

• 核心差异：输入格式不同（n行输入/一行输入），C3与C1输入格式一致且重复；前两题核心区别在于设备读数的输入方式，C1用Scanner逐行读取，C2用自定义快速输入类读取一行数据。
• 核心算法：一致采用「基于差分的贪心策略」，通过计算相邻元素差值的正负累加得到最少操作次数，基于首尾元素差值得到可能的最终读数种类数。
• 优化点：C2中自定义F类处理输入，避免Scanner的IO低效问题；当n≤1时直接返回结果，减少无效计算，适配n=1e5的大数据量。

C1-设备读数分n行输入

题目描述：在未来的数据中心中，所有服务器的数据读数必须保持一致。你被任命为"数据校准员"，负责调整一组设备的读数，使它们完全相同。一次操作中，你可以选择任意一个连续的设备区间[l, r]，让这些设备的读数同时增加1或减少1。你的目标是用最少的操作次数让所有设备的读数完全一致。同时，你还需要计算：在最优操作次数下，最终所有设备读数可能是多少种不同的值。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 第一行输入一个正整数n，表示设备数量。
• 接下来n行，每行输入一个整数aᵢ，表示第i台设备的初始读数。

输出格式：

• 第一行输出使所有设备读数相同所需的最少操作次数。
• 第二行输出在最少操作下，可能得到的不同最终读数种类数。

输入输出样例：

• 样例1：
  输入 ：

  4
  1
  1
  2
  2

  输出 ：

  1
  2

  说明：第一种：[1,2]同时加1，此时值全为2；第二种：[3,4]同时减1，此时值全为1。即最少操作数为1，种类有2种

• 样例2：
  输入 ：

  5
  3
  3
  3
  3
  3

  输出 ：

  0
  1

  说明：所有数相同，不需要操作，种类只有一种。

修改后代码：

import java.util.Scanner;
import java.lang.Math;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        if (!scanner.hasNext()) {
            scanner.close();
            return;
        }

        // 读取设备数量
        int deviceCount = scanner.nextInt();
        long[] data = new long[deviceCount];

        // 读取每台设备的读数（分n行输入）
        for (int i = 0; i < deviceCount; i++) {
            data[i] = scanner.nextLong();
        }
        scanner.close();

        // 处理设备数量为1的特殊情况
        if (deviceCount == 1) {
            System.out.println(0);
            System.out.println(1);
            return;
        }

        long upSum = 0; // 记录正差值总和（需要增加的操作）
        long downSum = 0; // 记录负差值总和（需要减少的操作）

        // 计算相邻设备读数的差值
        for (int i = 1; i < deviceCount; i++) {
            long diff = data[i] - data[i - 1];
            if (diff > 0) {
                // 后一个比前一个大，累加需要增加的操作数
                upSum += diff;
            } else if (diff < 0) {
                // 后一个比前一个小，累加需要减少的操作数（取绝对值）
                downSum += -diff;
            }
            // 差值为0时无需处理
        }

        // 最少操作次数为正负差值总和的最大值
        long minOperations = Math.max(upSum, downSum);
        // 可能的最终读数种类数 = 正负差值总和的绝对值 + 1
        long resultTypes = Math.abs(upSum - downSum) + 1;

        // 输出结果
        System.out.println(minOperations);
        System.out.println(resultTypes);
    }
}

C2-设备读数一行输入

题目描述：在不久的未来，全球最大的科技公司正在建设一座庞大的量子计算数据中心，负责处理各类复杂的计算任务。数据中心内有数以万计的服务器，它们的读数需要保持高度一致，才能保证数据处理的精度和效率。你被公司任命为"数据校准员"，负责调整这组服务器的读数，确保它们在最短的时间内完全一致。每当你进行一次调整时，你可以选择任意一个连续的服务器区间[l, r]，并对这段区间内的所有设备的读数同时执行增减操作，即所有设备的读数要么同时增加1，要么同时减少1。在执行调整操作时，你的目标是最小化操作次数，使得所有服务器的读数在最少的操作中达到一致。同时，考虑到设备的复杂性，最终所有设备的读数可能存在多种不同的值，而你的任务不仅仅是调整读数，还要计算最优操作下，最终所有设备的读数可能出现的不同的结果。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 第一行输入一个正整数n，表示设备数量。
• 接下来n个aᵢ，表示第i台设备的初始读数。

输出格式：

• 输出使所有设备读数相同所需的最少操作次数。隔一个空格输出在最少操作下，可能得到的不同最终读数种类数。

输入输出样例：

• 样例1：
  输入 ：

  3
  1 2 3

  输出 ：

  2 3

  说明：第一种：【1，2】加1，【1，1】加1，值全为3；第二种：【2，3】减1，【3，3】减1，值全为1；第三种：【1，1】加1，【3，3】减1，值全为2。

• 样例2：
  输入 ：

  5
  3 3 3 3 3

  输出 ：

  0 1

  说明：所有数相同，不需要操作，种类只有一种。

修改后代码：

import java.io.*;

public class Main {
    // 自定义快速输入类，适配一行输入多个数据
    static class FastReader {
        private final InputStream input;
        private final byte[] buffer = new byte[1 << 16];
        private int bufferPtr = 0;
        private int bufferLength = 0;

        public FastReader(InputStream input) {
            this.input = input;
        }

        // 读取一个长整数
        public long readLong() throws IOException {
            int byteCode = readByte();
            // 跳过空白字符（空格、制表符等）
            while (byteCode <= ' ' && byteCode != -1) {
                byteCode = readByte();
            }

            int sign = 1;
            if (byteCode == '-') {
                sign = -1;
                byteCode = readByte();
            }

            long num = 0;
            while (byteCode > ' ' && byteCode != -1) {
                num = num * 10 + (byteCode - '0');
                byteCode = readByte();
            }
            return num * sign;
        }

        // 读取一个字节
        private int readByte() throws IOException {
            if (bufferPtr >= bufferLength) {
                bufferLength = input.read(buffer);
                bufferPtr = 0;
                if (bufferLength <= 0) {
                    return -1;
                }
            }
            return buffer[bufferPtr++];
        }

        // 读取一个整数
        public int readInt() throws IOException {
            return (int) readLong();
        }
    }

    public static void main(String[] args) throws Exception {
        FastReader reader = new FastReader(System.in);
        int deviceCount;

        try {
            deviceCount = reader.readInt();
        } catch (Exception e) {
            System.out.println("0 1");
            return;
        }

        // 处理设备数量≤1的情况
        if (deviceCount <= 1) {
            System.out.println("0 1");
            return;
        }

        // 读取一行中的n个设备读数
        long[] serverData = new long[deviceCount];
        for (int i = 0; i < deviceCount; i++) {
            serverData[i] = reader.readLong();
        }

        long totalDiff = 0;
        // 计算所有相邻设备读数的绝对差值总和
        for (int i = 0; i + 1 < deviceCount; i++) {
            long diff = serverData[i + 1] - serverData[i];
            totalDiff += Math.abs(diff);
        }

        // 计算首尾设备读数的绝对差值
        long firstLastDiff = Math.abs(serverData[deviceCount - 1] - serverData[0]);

        // 最少操作次数 = (总相邻差值 + 首尾差值) / 2
        long minOps = (totalDiff + firstLastDiff) / 2;
        // 可能的最终读数种类数 = 首尾差值 + 1
        long resultCount = firstLastDiff + 1;

        // 输出结果（空格分隔）
        System.out.println(minOps + " " + resultCount);
    }
}

D-灯带/灯珠问题

相似题目差异总结：

• 核心差异：灯带形态不同（环形/直线形），D3与D1形态一致且重复；前两题核心区别在于是否需要考虑首尾相邻约束，环形需额外验证首尾衔接的状态合法性。
• 核心算法：一致采用「状态压缩+矩阵快速幂」策略，将连续m-1个灯珠的亮灭状态压缩为整数，通过矩阵乘法表示状态转移，快速幂加速n=1e15的大规模计算。
• 优化点：状态压缩减少空间复杂度（状态数为2^(m-1)），矩阵乘法中跳过0元素减少计算量，取模操作（1e9+7）避免溢出，适配m≤5的约束。

D1-灯带为环形（首尾相邻）

题目描述 ：小荞有一条环形的LED装饰灯带，共有n个灯珠，沿着环形依次编号为1~n（灯珠1和灯珠n相邻）。每个灯珠可以独立切换"亮"（用1表示）或"灭"（用0表示）两种状态。灯带的控制芯片有一个严格的节能规则：从任意一个灯珠开始，沿顺时针方向连续查看m个灯珠，这m个灯珠中处于"亮"状态的数量，不能超过k个。请你帮小荞计算一下，符合上述节能规则的灯带亮灯模式一共有多少种？结果需对 1 0 9 + 7 10^9 + 7 109+7取模后输出。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 一行包含三个整数n、m、k，分别代表灯珠总数、连续查看的灯珠数、亮灯的最大允许数量。

输出格式：

• 一行输出一个整数，表示符合规则的亮灯模式种数对 1 0 9 + 7 10^9 + 7 109+7取模的结果。

输入输出样例：

• 样例1：
  输入 ：

  6 4 2

  输出 ：

  24

  解释：满足所有约束的亮灯模式共24种。简单理解：6个灯的总亮灯数不能太多（否则连续4个会超2），也不能在局部集中亮灯。例如：亮2个灯：任意不相邻的2个灯（或相邻但不导致连续4个超2），均合法；亮3个灯：需分散排列（如灯1、3、5），避免4个连续灯中包含3个亮灯；亮0、1个灯：全部合法合法，但总模式数需结合环形约束去重（避免重复计数）。最终统计所有合法组合，共24种。

• 样例2：
  输入 ：

  20 5 2

  输出 ：

  15910

  解释：简单理解：20个灯组成环形，任意连续5个灯里亮灯数不能超2，满足这个要求的亮灯模式共15910种。具体看亮灯情况：亮0个灯：只有1种（全灭），合法；亮1个灯：20种（任意一个灯亮），合法（连续5个里最多1个亮）；亮2个灯：任意两个灯，不管相邻与否都合法（连续5个里最多2个亮），共C(20,2)=190种；亮3个灯：需分散排，不能让任意5个连续灯里包含这3个（比如每隔6个灯亮一个），合法模式有几百种；亮4个灯：更分散，比如按"亮1个、隔4个、亮1个"的规律排，避免5个连续灯里凑够3个亮灯，合法模式有几千种；亮5个及以上灯：只要排列足够分散（比如每4个灯里亮1个），也有大量合法模式；亮灯太集中（比如连续3个灯亮）：会导致包含它们的5个连续灯亮灯数超2，直接违法。最终把所有合法的亮灯模式（从亮0个到亮5个+）统计起来，总共是15910种。

修改后代码：

import java.io.*;
import java.util.*;

public class Main {
    private static final long MOD = 1000000007L;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer tokenizer = new StringTokenizer(br.readLine());
        
        long lampCount = Long.parseLong(tokenizer.nextToken());
        int windowSize = Integer.parseInt(tokenizer.nextToken());
        int maxOnCount = Integer.parseInt(tokenizer.nextToken());
        
        int stateLen = windowSize - 1; // 状态长度为m-1
        int stateCount = 1 << stateLen; // 状态总数：2^(m-1)

        // 构建状态转移矩阵
        long[][] transferMatrix = buildTransferMatrix(stateLen, stateCount, maxOnCount);

        // 计算转移矩阵的 (n - (m-1)) 次幂
        long steps = lampCount - (windowSize - 1);
        long[][] matrixPower = matrixPower(transferMatrix, steps, stateCount);

        // 预处理每个状态的二进制位（便于后续判断合法性）
        int[][] stateBits = preprocessStateBits(stateCount, stateLen);

        // 统计所有合法的环形模式
        long validPatterns = countValidRingPatterns(matrixPower, stateCount, stateLen, windowSize, maxOnCount, stateBits);

        System.out.println(validPatterns % MOD);
    }

    // 构建状态转移矩阵
    private static long[][] buildTransferMatrix(int stateLen, int stateCount, int maxOnCount) {
        long[][] transfer = new long[stateCount][stateCount];
        for (int currState = 0; currState < stateCount; currState++) {
            int onCount = Integer.bitCount(currState); // 当前状态中亮灯数量
            // 尝试添加0或1作为下一个灯珠状态
            for (int nextBit = 0; nextBit <= 1; nextBit++) {
                // 亮灯总数不超过maxOnCount则允许转移
                if (onCount + nextBit <= maxOnCount) {
                    // 计算新状态：左移1位并保留低stateLen位，最低位为nextBit
                    int newState = ((currState << 1) & (stateCount - 1)) | nextBit;
                    transfer[currState][newState]++;
                }
            }
        }
        return transfer;
    }

    // 矩阵乘法
    private static long[][] matrixMultiply(long[][] a, long[][] b, int size) {
        long[][] result = new long[size][size];
        for (int i = 0; i < size; i++) {
            for (int k = 0; k < size; k++) {
                long aVal = a[i][k];
                if (aVal == 0) continue; // 跳过0元素优化
                for (int j = 0; j < size; j++) {
                    long bVal = b[k][j];
                    if (bVal == 0) continue; // 跳过0元素优化
                    result[i][j] = (result[i][j] + aVal * bVal) % MOD;
                }
            }
        }
        return result;
    }

    // 矩阵快速幂
    private static long[][] matrixPower(long[][] matrix, long power, int size) {
        // 初始化单位矩阵
        long[][] identity = new long[size][size];
        for (int i = 0; i < size; i++) {
            identity[i][i] = 1;
        }

        while (power > 0) {
            if ((power & 1) == 1) {
                identity = matrixMultiply(identity, matrix, size);
            }
            matrix = matrixMultiply(matrix, matrix, size);
            power >>= 1;
        }
        return identity;
    }

    // 预处理每个状态的二进制位（按从高位到低位的顺序）
    private static int[][] preprocessStateBits(int stateCount, int stateLen) {
        int[][] bits = new int[stateCount][stateLen];
        for (int state = 0; state < stateCount; state++) {
            for (int i = 0; i < stateLen; i++) {
                // 提取第 (stateLen - 1 - i) 位的二进制值
                bits[state][i] = (state >> (stateLen - 1 - i)) & 1;
            }
        }
        return bits;
    }

    // 统计环形灯带的合法模式数
    private static long countValidRingPatterns(long[][] matrixPower, int stateCount, int stateLen, int windowSize, int maxOnCount, int[][] stateBits) {
        long total = 0;
        for (int startState = 0; startState < stateCount; startState++) {
            int[] startBits = stateBits[startState];
            for (int endState = 0; endState < stateCount; endState++) {
                long ways = matrixPower[startState][endState];
                if (ways == 0) continue; // 无此转移路径则跳过

                int[] endBits = stateBits[endState];
                boolean isValid = true;

                // 验证首尾衔接的连续m个灯珠是否合法
                for (int tLen = 1; tLen <= stateLen; tLen++) {
                    int tailLen = windowSize - tLen;
                    int onTotal = 0;

                    // 统计endState的后tailLen位
                    for (int i = stateLen - tailLen; i < stateLen; i++) {
                        onTotal += endBits[i];
                    }

                    // 统计startState的前tLen位
                    for (int i = 0; i < tLen; i++) {
                        onTotal += startBits[i];
                    }

                    // 亮灯数超过阈值则不合法
                    if (onTotal > maxOnCount) {
                        isValid = false;
                        break;
                    }
                }

                if (isValid) {
                    total = (total + ways) % MOD;
                }
            }
        }
        return total;
    }
}

D2-灯带为直线形（首尾不相邻）

题目描述 ：小夏入手了一条直线形的智能氛围灯，灯带上镶嵌着n个可独立控光的灯珠，按安装顺序依次标记为1到n。每个灯珠都能实现"常亮"（对应状态码1）和"休眠"（对应状态码0）两种模式的自由切换。为保障设备低功耗运行，灯控系统内置了严苛的能耗校验逻辑：从任意一个灯珠的位置出发，沿灯带延伸方向依次选取连续的m个灯珠（若当前位置后续剩余灯珠数量不足m个，则跳过该次校验），每次选取的这组m个灯珠中，处于"常亮"模式的灯珠数量，必须控制在k个及以内。请帮小夏计算，所有满足上述能耗校验逻辑的灯珠亮灭模式组合共有多少种？计算结果需按 1 0 9 + 7 10^9 + 7 109+7取模后输出。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 一行包含三个整数n、m、k，分别表示灯带上灯珠的总数量、每次校验选取的连续灯珠个数、单组校验中允许常亮的灯珠最大数量。

输出格式：

• 一行输出一个整数，表示符合规则的亮灯模式种数对 1 0 9 + 7 10^9 + 7 109+7取模的结果。

输入输出样例：

• 样例1：
  输入 ：

  2 2 1

  输出 ：

  3

  解释：长度2，窗口长度2，最多允许1个1→禁止子串11。长度2的二进制串共有00,01,10,11，去掉11，所以答案3。

• 样例2：
  输入 ：

  3 2 1

  输出 ：

  5

  解释：要求任意相邻的两个灯珠不能同时为1（即没有连续11）。长度3的合法串为000,001,010,100,101，共5种。

修改后代码：

import java.util.Scanner;

public class Main {
    private static final long MOD = 1000000007L;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        if (!scanner.hasNext()) {
            scanner.close();
            System.out.println(0);
            return;
        }

        long lampTotal = scanner.nextLong();
        int checkWindow = scanner.nextInt();
        int maxOn = scanner.nextInt();
        scanner.close();

        int stateSize = 1 << (checkWindow - 1); // 状态数：2^(m-1)

        // 构建状态转移矩阵
        long[][] transMatrix = createTransitionMatrix(stateSize, checkWindow, maxOn);

        // 初始化结果矩阵为单位矩阵
        long[][] resultMatrix = new long[stateSize][stateSize];
        for (int i = 0; i < stateSize; i++) {
            resultMatrix[i][i] = 1;
        }

        // 计算转移矩阵的 (n - m + 1) 次幂
        long power = lampTotal - checkWindow + 1;
        while (power > 0) {
            if ((power & 1) == 1) {
                resultMatrix = multiplyMatrices(resultMatrix, transMatrix, stateSize);
            }
            transMatrix = multiplyMatrices(transMatrix, transMatrix, stateSize);
            power >>= 1;
        }

        // 统计所有合法模式数（所有状态转移路径之和）
        long validPatterns = 0;
        for (int i = 0; i < stateSize; i++) {
            for (int j = 0; j < stateSize; j++) {
                validPatterns = (validPatterns + resultMatrix[i][j]) % MOD;
            }
        }

        System.out.println(validPatterns);
    }

    // 构建状态转移矩阵
    private static long[][] createTransitionMatrix(int stateSize, int window, int maxOn) {
        long[][] matrix = new long[stateSize][stateSize];
        for (int currState = 0; currState < stateSize; currState++) {
            // 尝试添加0或1作为下一个灯珠状态
            for (int nextBit = 0; nextBit <= 1; nextBit++) {
                // 计算当前状态+下一位的总亮灯数
                int totalOn = Integer.bitCount(currState) + nextBit;
                if (totalOn <= maxOn) {
                    // 生成新状态：左移1位并保留低 (window-1) 位，最低位为nextBit
                    int newState = ((currState << 1) | nextBit) & (stateSize - 1);
                    matrix[currState][newState] = 1;
                }
            }
        }
        return matrix;
    }

    // 矩阵乘法（适配模运算）
    private static long[][] multiplyMatrices(long[][] matA, long[][] matB, int size) {
        long[][] product = new long[size][size];
        for (int i = 0; i < size; i++) {
            for (int k = 0; k < size; k++) {
                long aVal = matA[i][k];
                if (aVal == 0) continue; // 跳过0元素优化计算
                for (int j = 0; j < size; j++) {
                    long bVal = matB[k][j];
                    if (bVal == 0) continue; // 跳过0元素优化计算
                    product[i][j] = (product[i][j] + aVal * bVal) % MOD;
                }
            }
        }
        return product;
    }
}

E-实时中位数问题

相似题目差异总结：

• 核心差异：输出要求不同（仅实时中位数/实时中位数+平均值），E3与E1输出要求一致且重复；前两题核心区别在于E2需额外记录全局最大/最小值，最终计算中位数与最大最小值的平均值。
• 核心算法：一致采用「双堆维护」策略，大根堆存储左半部分数据（小于等于中位数），小根堆存储右半部分数据（大于中位数），保持堆大小平衡以快速获取中位数。
• 优化点：使用PriorityQueue实现双堆，BufferedReader/StreamTokenizer提升输入速度，避免数据溢出（E2中用long存储总和），适配n=1e5的大数据量。

E1-仅输出每次录入后的实时中位数

题目描述：科研实验室在收集一组传感器数据。每当有新的测量值被记录，监控系统必须立刻计算当前所有数据的中位数（向下取整），用于实时显示实验波动趋势。小明被任命为"实时数据中位数统计员"。每一次测试数据录入系统后，他就要立刻报出当前所有数据的中位数（取下取整）。数据太多，小明算不过来了......他希望你帮他写一个程序来完成这个任务。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 第一行输入一个整数 N，表示数据数量。
• 第二行输入 N 个整数 a i a_i ai，依次表示每个数据。

输出格式：

• 输出 N 个整数，第 i 个数表示录入前 i 个数据后的中位数（取下取整），用空格分隔。

输入输出样例：

• 样例1：
  输入 ：

  5
  1 2 3 4 5

  输出 ：

  1 1 2 2 3

  说明：1->1；1 2->1；1 2 3->2；1 2 3 4->2；1 2 3 4 5->3。

• 样例2：
  输入 ：

  6
  3 7 2 10 5 6

  输出 ：

  3 5 3 5 5 5

  说明：3->3；3 7->5；2 3 7->3；2 3 7 10->5；2 3 5 7 10->5；2 3 5 6 7 10->5。

修改后代码：

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        // 初始化输入输出流，提升效率
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer tokenizer = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        // 读取数据数量
        tokenizer.nextToken();
        int dataCount = (int) tokenizer.nval;

        // 大根堆：存储左半部分数据（小于等于中位数）
        PriorityQueue<Integer> leftMaxHeap = new PriorityQueue<>(Collections.reverseOrder());
        // 小根堆：存储右半部分数据（大于中位数）
        PriorityQueue<Integer> rightMinHeap = new PriorityQueue<>();

        // 逐个处理输入数据
        for (int i = 0; i < dataCount; i++) {
            tokenizer.nextToken();
            int currentData = (int) tokenizer.nval;

            // 先加入大根堆，再平衡到小根堆（保证左堆元素≤右堆元素）
            leftMaxHeap.offer(currentData);
            rightMinHeap.offer(leftMaxHeap.poll());

            // 保持堆大小平衡：左堆大小 ≥ 右堆大小，且差值不超过1
            if (rightMinHeap.size() > leftMaxHeap.size()) {
                leftMaxHeap.offer(rightMinHeap.poll());
            }

            // 计算当前中位数
            int currMedian;
            if (leftMaxHeap.size() > rightMinHeap.size()) {
                // 奇数个数据，中位数为左堆顶
                currMedian = leftMaxHeap.peek();
            } else {
                // 偶数个数据，中位数为两堆顶平均值（向下取整）
                currMedian = (leftMaxHeap.peek() + rightMinHeap.peek()) / 2;
            }

            // 输出当前中位数（暂存到缓冲区）
            out.print(currMedian + " ");
        }

        // 刷新输出流，确保所有数据输出
        out.flush();
        out.close();
        br.close();
    }
}

E2-输出实时中位数及最终平均值

题目描述：在火星能源站的温度监控系统中，数百个传感器会不断上传实时温度读数。控制中心的系统每接收到一条新的温度数据，就必须立即计算并显示当前所有数据的中位温度（取下整）。作为系统维护员，你需要编写一个程序，帮助控制中心自动完成这一实时统计功能，并计算最后中位数与最大值，最小值的平均值。

运行条件：

• 总时限：5000毫秒
• 单组时限：1000毫秒
• 总内存：320 MB
• 单组内存：64 MB

输入格式：

• 第一行输入一个整数N，表示数据数量。
• 第二行输入N个整数 a i a_i ai，依次表示每个数据。

输出格式：

• 第一行输出N个整数，第i个数表示录入前i个数据后的中位数（取下取整），用空格分隔。
• 第二行输出平均值（向下取整）。

输入输出样例：

• 样例1：
  输入 ：

  4
  10 9 8 7

  输出 ：

  10 9 9 8
  8

  说明：10->10；9 10->9；8 9 10->9；7 8 9 10->8。最大值10，最小值：7，中位数：8。平均值为(10+7+8)/3=8。

• 样例2：
  输入 ：

  6
  3 7 2 10 5 6

  输出 ：

  3 5 3 5 5 5
  5

  说明：3->3；3 7->5；2 3 7->3；2 3 7 10->5；2 3 5 7 10->5；2 3 5 6 7 10->5。最大值10，最小值：2，中位数：5。平均值为(10+2+5)/3=5。

修改后代码：

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        // 高效输入输出配置
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer st = new StreamTokenizer(br);
        PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));

        // 读取数据总数
        st.nextToken();
        int totalCount = (int) st.nval;

        // 双堆维护中位数：左堆大根堆，右堆小根堆
        PriorityQueue<Integer> leftHeap = new PriorityQueue<>(Collections.reverseOrder());
        PriorityQueue<Integer> rightHeap = new PriorityQueue<>();

        int maxVal = Integer.MIN_VALUE; // 全局最大值
        int minVal = Integer.MAX_VALUE; // 全局最小值
        int finalMedian = 0; // 最后一次的中位数

        for (int i = 0; i < totalCount; i++) {
            st.nextToken();
            int data = (int) st.nval;

            // 更新全局最大最小值
            if (data > maxVal) {
                maxVal = data;
            }
            if (data < minVal) {
                minVal = data;
            }

            // 插入数据并平衡双堆
            leftHeap.offer(data);
            rightHeap.offer(leftHeap.poll());

            // 保证左堆大小 ≥ 右堆大小
            if (rightHeap.size() > leftHeap.size()) {
                leftHeap.offer(rightHeap.poll());
            }

            // 计算当前中位数
            if (leftHeap.size() > rightHeap.size()) {
                finalMedian = leftHeap.peek();
            } else {
                finalMedian = (leftHeap.peek() + rightHeap.peek()) / 2;
            }

            // 输出当前中位数
            pw.print(finalMedian + " ");
        }

        // 计算并输出平均值（向下取整）
        long sum = (long) maxVal + minVal + finalMedian;
        int avg = (int) (sum / 3);

        pw.println();
        pw.print(avg);

        // 刷新并关闭流
        pw.flush();
        pw.close();
        br.close();
    }
}