线代第二章矩阵第二课：矩阵的加法、减法、数乘

矩阵的加法、减法与数乘运算

矩阵的加法、减法、数乘统称为矩阵的线性运算，运算结果仍为矩阵，以下是详细规则和示例。

一、 前提：同型矩阵的定义

矩阵的加法、减法运算，仅对同型矩阵有效。

• 同型矩阵 ：两个矩阵的行数相等且列数相等 ，例如 和 是同型矩阵； 和 不是同型矩阵。

二、 矩阵的加法

1. 定义

设同型矩阵 ，，则矩阵 A 与 B 的和记作 A+B，定义为：

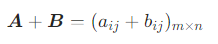
即对应位置的元素相加，得到一个新的 m×n 矩阵。

2. 运算性质

设 都是 m×n 矩阵（ 为零矩阵），则：

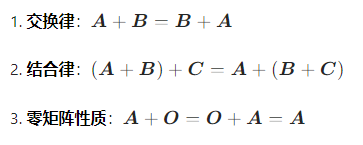
3. 示例

已知

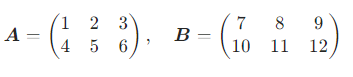
则

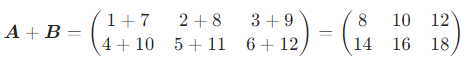
三、 矩阵的减法

1. 定义

矩阵减法是加法的逆运算，先定义负矩阵 ：对矩阵 ，其负矩阵为

即每个元素取相反数。

同型矩阵 A 与 B 的差记作 A−B，定义为：

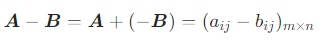
即 对应位置的元素相减。

2. 运算性质

设 A,B 是同型矩阵，则：

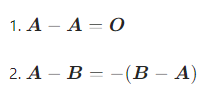
3. 示例

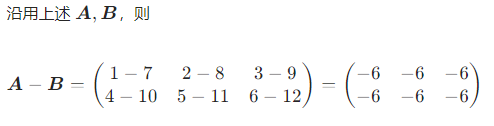
四、 矩阵的数乘

1. 定义

设 k 是任意常数（实数或复数），矩阵 ​，则数 k 与矩阵 A 的乘积记作 ，定义为：

即 用数 k 乘以矩阵的每一个元素，结果仍为 m×n 矩阵。

2. 运算性质

3. 示例

五、 线性运算的综合示例

内容来源-B站宋浩老师