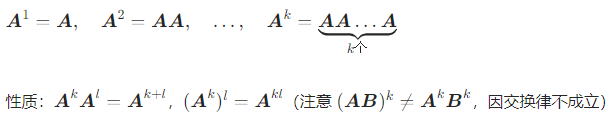线代第二章矩阵第三课：矩阵乘法

矩阵乘法

矩阵乘法是矩阵运算中最核心且规则特殊的运算，与普通数的乘法差异较大，其结果是一个新矩阵，且有严格的运算前提。

一、 运算前提：矩阵的行列匹配

只有当第一个矩阵的列数 等于第二个矩阵的行数时，两个矩阵才能相乘。设矩阵 A 是 m×s 矩阵，矩阵 B 是 s×n 矩阵，则乘积 AB 是一个 m×n 矩阵。简单记为：(m×s)×(s×n)=(m×n)

注：若 A 的列数 ≠ B 的行数，则 AB 无意义。

二、 定义：元素的计算规则

设 ，，乘积 ，其中第 i 行第 k 列的元素 的计算公式为：

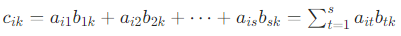
通俗理解：C 的元素 ​ 是 A 的第 i 行 与 B 的第 k 列对应元素相乘后求和（即 "行乘列" 法则）。

三、 示例

1. 二阶方阵 × 二阶方阵

已知

因此

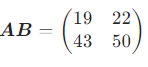
2. 非方阵乘法（2×3 矩阵 × 3×2 矩阵）

已知

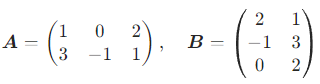
A 是 2×3，B 是 3×2，乘积 AB 是 2×2 矩阵：

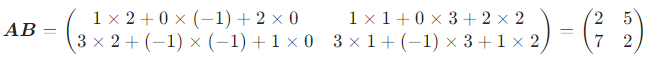
四、 矩阵乘法的核心性质

矩阵乘法与数的乘法有明显区别，以下是关键性质：

1. 不满足交换律 ：一般情况下
   • 可能 AB 有意义，但 BA 无意义（如 2×3 矩阵 × 3×2 矩阵，AB 是 2×2，BA 是 3×3）；
   • 即使 AB 和 BA 都有意义，结果也可能不同（如上述二阶方阵示例，可自行计算 BA 验证）。
2. 满足结合律：(AB)C=A(BC)（前提是运算有意义）
3. 满足分配律
   • 左分配律：A(B+C)=AB+AC
   • 右分配律：(B+C)A=BA+CA
4. 数乘结合律 ：（k 为常数）
5. 单位矩阵的作用 ：对任意 m×n 矩阵 A，有 （E 为单位矩阵）
6. 零矩阵的作用 ：若 A 是 m×s 矩阵，O 是 s×n 零矩阵，则 ；反之同理。
7. 注意：AB=O⇏A=O 或 B=O，例如：

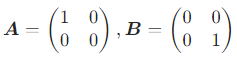
AB=O 但 A,B 都不是零矩阵

五、 特殊情况：方阵的幂

若 A 是 n 阶方阵，则可定义 A 的幂：