机器学习进阶＜1＞像侦探一样思考——朴素贝叶斯分类器全解析

一、引言

在信息爆炸的时代，我们每天都需要对海量数据进行分类和判断：垃圾邮件过滤、新闻分类、情感分析......这些看似复杂的任务背后，往往隐藏着一个简单而强大的算法------朴素贝叶斯分类器。今天，让我们一起化身"数据侦探"，揭开这个算法的神秘面纱。

二、侦探破案：从直觉到算法

1. 一个引人入胜的案例

想象你是一位侦探，犯罪现场发现了两个关键线索：猫毛和窗外脚印。你的经验库告诉你：

• 60%的案件是"爱猫人士A"所为，且A作案时80%会留下猫毛

• 40%的案件是"运动达人B"所为，且B作案时90%会留下脚印

问题来了：基于这两个证据，凶手更可能是谁？

我们的大脑会自然地结合"先验经验"（谁犯案多）和"新证据"（线索）进行判断------这正是朴素贝叶斯的核心思想！

2. 算法与直觉的契合

朴素贝叶斯就像一个"概率侦探"，它计算的是：在拥有某些特征的情况下，样本属于某个类别的概率。与我们破案的思维过程不谋而合。

三、侦探工具箱：核心概念全解析

3.1 贝叶斯定理：信念更新器

核心公式（简化版）：

新信念（后验概率） ∝ 旧信念（先验概率） × 证据强度（似然）
P(类别|特征) ∝ P(类别) × P(特征|类别)

通俗解释：

• 先验概率：基于历史经验的初始判断（如"A犯案概率60%"）

• 似然：如果假设成立，观察到当前证据的概率（如"如果是A，留下猫毛的概率"）

• 后验概率：结合证据后的更新判断

关键洞察：我们通常不需要精确计算概率值，只需比较不同类别的相对大小就能做出决策。

3.2 "朴素"的智慧：特征独立假设

现实问题：判断邮件是否垃圾邮件时，"发票"和"免费"两个词可能同时出现，它们之间可能存在关联。

朴素假设：为了简化计算，算法"天真地"假设所有特征相互独立。即：

P("发票"和"免费"|垃圾邮件) = P("发票"|垃圾邮件) × P("免费"|垃圾邮件)

辩证看待：

• 优点：极大简化计算，使算法高效可行

• 缺点：现实世界中特征往往相关，这是算法的主要局限性

• 实际效果：尽管假设很强，但在许多场景下表现优异！

3.3 办案全流程：三步走策略

1. 收集案底（训练阶段）

   • 统计各类别的先验概率

   • 计算每个特征在各个类别下的条件概率

2. 分析新线索（预测阶段）

   • 提取新样本的特征

   • 将特征转化为概率计算所需的输入

3. 计算并判决

   • 计算样本属于每个类别的相对概率

   • 选择概率最大的类别作为预测结果

四、实战演练：手算朴素贝叶斯

4.1 案例：水果分类器

训练数据：

|--------|-------------|-------------|
| 水果 | 颜色（黄/红） | 形状（长/圆） |
| 香蕉 | 黄 | 长 |
| 香蕉 | 黄 | 长 |
| 苹果 | 红 | 圆 |
| 苹果 | 红 | 圆 |
| 香蕉 | 黄 | 长 |
| 苹果 | 红 | 圆 |

4.2 逐步计算

Step 1: 计算先验概率

P(苹果) = 3/6 = 0.5
P(香蕉) = 3/6 = 0.5

Step 2: 计算条件概率（平滑前）

P(颜色=黄|香蕉) = 3/3 = 1
P(形状=长|香蕉) = 3/3 = 1
P(颜色=黄|苹果) = 0/3 = 0 ← 遇到零概率问题！
P(形状=圆|苹果) = 3/3 = 1

4.3 零概率问题与拉普拉斯平滑

问题：如果某个特征在某个类别中从未出现，其条件概率为0，会导致整个后验概率为0。

解决方案：拉普拉斯平滑（Laplace Smoothing）

• 思想：假设每个特征至少出现一次

• 操作：分子加1，分母加特征的可能取值数

平滑后计算：

P(颜色=黄|苹果) = (0+1) / (3+2) = 1/5
P(颜色=红|苹果) = (3+1) / (3+2) = 4/5
P(形状=圆|苹果) = (3+1) / (3+2) = 4/5
P(颜色=黄|香蕉) = (3+1) / (3+2) = 4/5
P(形状=长|香蕉) = (3+1) / (3+2) = 4/5

4.4 对新样本分类

新样本：颜色=黄，形状=圆

计算比较：

P(苹果|黄,圆) ∝ P(苹果) × P(黄|苹果) × P(圆|苹果)
              ∝ 0.5 × (1/5) × (4/5) = 0.08

P(香蕉|黄,圆) ∝ P(香蕉) × P(黄|香蕉) × P(圆|香蕉)
              ∝ 0.5 × (4/5) × (1/5) = 0.08

结果：两者概率相等！这个有趣的结果说明，在某些边界情况下，朴素贝叶斯可能需要更多特征或数据来做出明确判断。

五、编程实战：用Python实现文本分类

5.1 环境准备

# 导入必要的库
from sklearn.naive_bayes import MultinomialNB  # 多项式朴素贝叶斯，适合文本分类
from sklearn.feature_extraction.text import CountVectorizer  # 文本特征提取
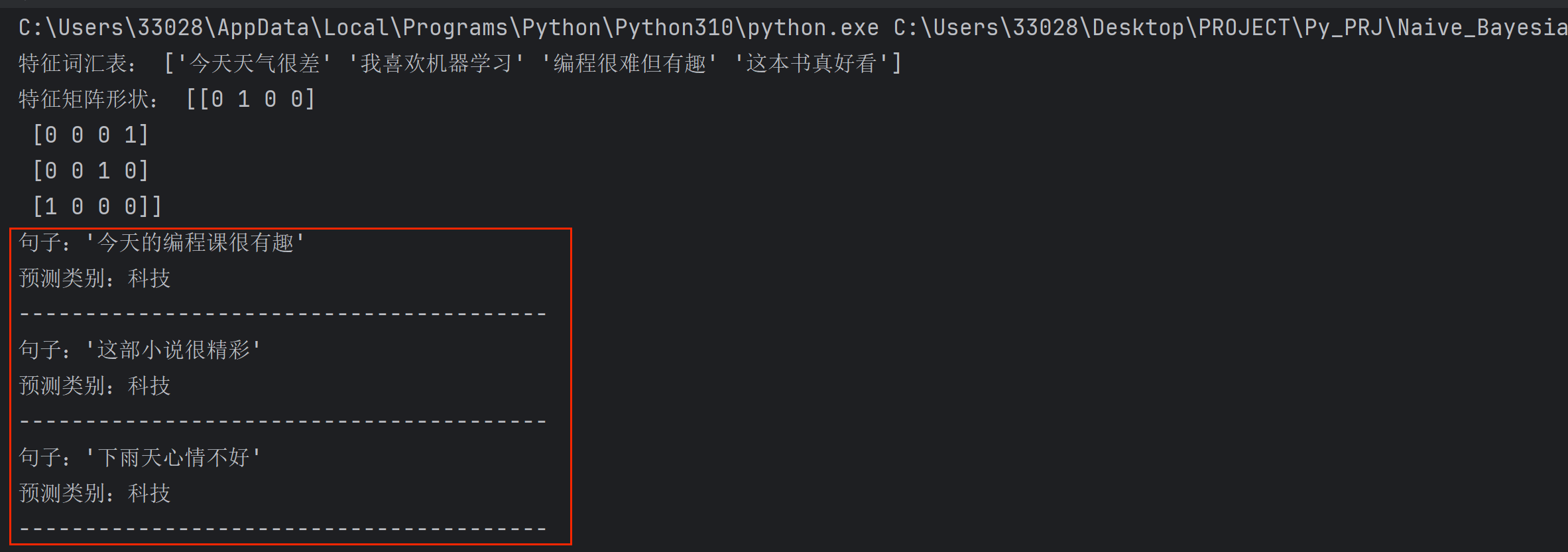
import pandas as pd

第一段代码主要完成了朴素贝叶斯文本分类器的训练过程。

首先，代码导入了必要的机器学习库，包括用于文本分类的MultinomialNB和用于文本特征提取的CountVectorizer。接着，定义了包含四个句子的训练数据集及其对应的类别标签（科技、文艺、生活）。

然后，通过CountVectorizer将文本数据转换为数值特征矩阵，这一步骤将每个句子转换为词频向量。

最后，使用这些特征训练了一个多项式朴素贝叶斯分类器，构建了一个能够根据文本内容预测类别的分类模型。

5.2 完整代码示例

# 1. 准备训练数据（案底库）
train_data = [
    "我喜欢机器学习",  # 科技类
    "这本书真好看",    # 文艺类
    "编程很难但有趣",  # 科技类
    "今天天气很差"     # 生活类
]
train_label = ["科技", "文艺", "科技", "生活"]  # 对应类别

# 2. 文本特征提取（将文字线索数字化）
vectorizer = CountVectorizer()
X_train = vectorizer.fit_transform(train_data)

# 查看特征词汇表
print("特征词汇表：", vectorizer.get_feature_names_out())
print("特征矩阵形状：", X_train.toarray())

# 3. 训练朴素贝叶斯分类器
detective = MultinomialNB()
detective.fit(X_train, train_label)

# 4. 对新样本进行分类
new_texts = ["今天的编程课很有趣", "这部小说很精彩", "下雨天心情不好"]
X_new = vectorizer.transform(new_texts)

# 5. 预测并展示结果
predictions = detective.predict(X_new)
for text, category in zip(new_texts, predictions):
    print(f"句子：'{text}'")
    print(f"预测类别：{category}")
    print("-" * 40)

# 额外：获取预测概率
probabilities = detective.predict_proba(X_new)
print("\n预测概率详情：")
for i, text in enumerate(new_texts):
    print(f"\n'{text}'：")
    for j, category in enumerate(detective.classes_):
        print(f"  {category}: {probabilities[i][j]:.3f}")

第二段代码展示了如何使用训练好的朴素贝叶斯分类器进行新文本的分类预测。代码首先定义了三个新文本作为测试样本，并使用之前训练好的特征转换器将这些文本转换为特征向量。接着，调用训练好的分类器进行类别预测，并逐个输出每个文本的预测结果。最后，通过predict_proba方法获取了每个文本属于各个类别的详细概率分布，这不仅展示了模型的最终分类决策，还揭示了模型对不同类别的置信程度，有助于更深入地理解分类器的决策过程。

5.3 代码解读

1. 特征提取 ：CountVectorizer将文本转换为词频矩阵

2. 模型训练 ：MultinomialNB适用于离散特征（如词频）

3. 预测分析 ：predict_proba方法可以查看各类别的概率值

5.4 运行结果分析

通过输出结果，我们可以看到：

• 模型如何将新句子分类到不同类别

• 每个预测背后的概率分布

• 哪些特征对分类决策影响最大

六、算法深度解析

6.1 三种常见的朴素贝叶斯变体

1. 高斯朴素贝叶斯：假设特征服从正态分布，适用于连续特征

2. 多项式朴素贝叶斯：适用于离散特征和文本分类（我们示例中使用）

3. 伯努利朴素贝叶斯：特征为二值变量（出现/不出现）

6.2 优缺点总结

优点：

• 算法简单，易于实现和理解

• 训练和预测速度快，适合大规模数据

• 对小规模数据表现良好

• 可以处理多分类问题

• 对缺失数据不敏感

缺点：

• 特征独立假设在实际中往往不成立

• 特征之间的关联信息会被忽略

• 概率估计可能不够准确（尤其是小样本时）

6.3 应用场景

1. 文本分类：垃圾邮件过滤、情感分析、新闻分类

2. 推荐系统：基于内容的简单推荐

3. 医疗诊断：症状与疾病的关联分析

4. 实时检测系统：需要快速响应的场景

七、进阶思考与拓展

7.1 拉普拉斯平滑的深度理解

• 平滑系数选择：不一定是1，可以根据数据调整

• 系数影响：值越大，先验影响越大，模型越保守

• 实践建议：通常从1开始，通过交叉验证调整

下面我使用matlab语言将拉普拉斯平滑可视化：

%% 朴素贝叶斯拉普拉斯平滑可视化
clear; close all; clc;

%% 1. 创建示例数据 - 电影评论情感分析
% 特征：单词出现次数 (1:出现, 0:未出现)
% 类别：1=正面评价, 0=负面评价

% 训练数据
X_train = [
    1 1 0 1 0;  % 文档1: 包含单词1,2,4
    1 0 1 0 1;  % 文档2: 包含单词1,3,5
    0 1 1 1 0;  % 文档3
    0 0 1 0 1;  % 文档4
    1 1 0 0 0;  % 文档5
    0 1 1 0 1;  % 文档6
    1 0 0 1 1;  % 文档7
    0 1 0 1 0;  % 文档8
];

y_train = [1; 1; 1; 0; 1; 0; 1; 0];  % 类别标签

% 测试数据
X_test = [1 0 1 0 0; 0 1 0 1 1];  % 测试文档
y_test = [1; 0];  % 真实标签

% 单词名称
vocab = {'great', 'bad', 'awesome', 'terrible', 'good'};
num_features = size(X_train, 2);

fprintf('数据集信息:\n');
fprintf('训练样本数: %d\n', size(X_train, 1));
fprintf('特征数(单词数): %d\n', num_features);
fprintf('正面评价数: %d\n', sum(y_train == 1));
fprintf('负面评价数: %d\n', sum(y_train == 0));

%% 2. 计算拉普拉斯平滑前后的条件概率对比
fprintf('\n=== 拉普拉斯平滑对比 ===\n');

% 计算类先验
prior_pos = sum(y_train == 1) / length(y_train);
prior_neg = sum(y_train == 0) / length(y_train);

fprintf('先验概率: P(正面)=%.3f, P(负面)=%.3f\n', prior_pos, prior_neg);

% 计算不同alpha下的条件概率
alphas = [0, 0.5, 1, 2, 5, 10];  % 不同的平滑系数
num_alphas = length(alphas);

% 存储条件概率
cond_probs_pos = zeros(num_features, num_alphas);
cond_probs_neg = zeros(num_features, num_alphas);

for i = 1:num_alphas
    alpha = alphas(i);
    
    % 正面评价的条件概率
    for j = 1:num_features
        % 拉普拉斯平滑公式: (count + alpha) / (N + alpha * num_classes)
        count_pos = sum(X_train(y_train == 1, j) == 1);
        cond_probs_pos(j, i) = (count_pos + alpha) / (sum(y_train == 1) + alpha * 2);
    end
    
    % 负面评价的条件概率
    for j = 1:num_features
        count_neg = sum(X_train(y_train == 0, j) == 1);
        cond_probs_neg(j, i) = (count_neg + alpha) / (sum(y_train == 0) + alpha * 2);
    end
end

%% 3. 可视化拉普拉斯平滑的影响
figure('Position', [100, 100, 1400, 900]);

% 3.1 原始条件概率（无平滑）
subplot(2, 3, 1);
bar(cond_probs_pos(:, 1));
hold on;
bar(cond_probs_neg(:, 1), 0.6, 'r');
title('原始条件概率 (α=0)', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('单词索引');
ylabel('条件概率 P(单词|类别)');
set(gca, 'XTick', 1:num_features, 'XTickLabel', vocab, 'XTickLabelRotation', 45);
legend({'P(单词|正面)', 'P(单词|负面)'}, 'Location', 'best');
grid on;

% 标记零概率问题
zero_prob_idx = find(cond_probs_pos(:, 1) == 0 | cond_probs_neg(:, 1) == 0);
for idx = zero_prob_idx'
    text(idx, 0.05, '零概率', 'HorizontalAlignment', 'center', ...
         'BackgroundColor', 'yellow', 'FontWeight', 'bold');
end

% 3.2 平滑后的条件概率对比
subplot(2, 3, 2);
colors = lines(num_alphas);
for i = 1:num_alphas
    plot(1:num_features, cond_probs_pos(:, i), 'o-', ...
         'Color', colors(i,:), 'LineWidth', 1.5, 'MarkerSize', 6);
    hold on;
end
title('不同α下的 P(单词|正面)', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('单词索引');
ylabel('条件概率');
set(gca, 'XTick', 1:num_features, 'XTickLabel', vocab, 'XTickLabelRotation', 45);
legend(cellstr(num2str(alphas', 'α=%g')), 'Location', 'best');
grid on;

subplot(2, 3, 3);
for i = 1:num_alphas
    plot(1:num_features, cond_probs_neg(:, i), 's--', ...
         'Color', colors(i,:), 'LineWidth', 1.5, 'MarkerSize', 6);
    hold on;
end
title('不同α下的 P(单词|负面)', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('单词索引');
ylabel('条件概率');
set(gca, 'XTick', 1:num_features, 'XTickLabel', vocab, 'XTickLabelRotation', 45);
legend(cellstr(num2str(alphas', 'α=%g')), 'Location', 'best');
grid on;

% 3.3 平滑系数对特定单词概率的影响
subplot(2, 3, 4);
word_idx = 2;  % 选择单词'bad'
plot(alphas, cond_probs_pos(word_idx, :), 'b-o', 'LineWidth', 2, 'MarkerSize', 8);
hold on;
plot(alphas, cond_probs_neg(word_idx, :), 'r-s', 'LineWidth', 2, 'MarkerSize', 8);
title(sprintf('平滑系数对单词"%s"的影响', vocab{word_idx}), ...
      'FontSize', 12, 'FontWeight', 'bold');
xlabel('平滑系数 α');
ylabel('条件概率');
legend({'P(单词|正面)', 'P(单词|负面)'}, 'Location', 'best');
grid on;
xlim([min(alphas)-0.5, max(alphas)+0.5]);

% 3.4 平滑系数对零概率问题的影响
subplot(2, 3, 5);
zero_prob_before = sum(cond_probs_pos(:, 1) == 0) + sum(cond_probs_neg(:, 1) == 0);
zero_prob_after = zeros(1, num_alphas);

for i = 1:num_alphas
    zero_prob_after(i) = sum(cond_probs_pos(:, i) == 0) + sum(cond_probs_neg(:, i) == 0);
end

bar([zero_prob_before, zero_prob_after(2:end)]);
title('零概率问题消除情况', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('平滑系数 α');
ylabel('零概率出现次数');
set(gca, 'XTick', 1:num_alphas, 'XTickLabel', cellstr(num2str(alphas', '%g')));
grid on;

% 添加标注
for i = 1:num_alphas
    if i == 1
        text(i, zero_prob_before+0.1, sprintf('%d次', zero_prob_before), ...
             'HorizontalAlignment', 'center');
    else
        text(i, zero_prob_after(i)+0.1, sprintf('%d次', zero_prob_after(i)), ...
             'HorizontalAlignment', 'center');
    end
end

% 3.5 平滑系数对模型保守程度的影响
subplot(2, 3, 6);
% 计算概率的方差 - 衡量模型保守程度
prob_variance = zeros(1, num_alphas);
for i = 1:num_alphas
    all_probs = [cond_probs_pos(:, i); cond_probs_neg(:, i)];
    prob_variance(i) = var(all_probs);
end

plot(alphas, prob_variance, 'k-^', 'LineWidth', 2, 'MarkerSize', 8);
title('平滑系数对模型保守程度的影响', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('平滑系数 α');
ylabel('概率分布的方差');
grid on;
xlim([min(alphas)-0.5, max(alphas)+0.5]);

% 添加解释文本
annotation('textbox', [0.05, 0.01, 0.9, 0.05], ...
           'String', '方差越小 → 概率分布越均匀 → 模型越保守（避免过度自信）', ...
           'FontSize', 10, 'FontWeight', 'bold', ...
           'BackgroundColor', [0.9, 0.95, 1], ...
           'EdgeColor', 'blue', 'LineWidth', 1);

%% 4. 测试不同alpha值的性能
fprintf('\n=== 朴素贝叶斯分类器性能对比 ===\n');

% 测试不同alpha值的性能
fprintf('\n不同平滑系数的性能对比:\n');
fprintf('α\t训练准确率\t测试准确率\t平均置信度\n');
fprintf('----------------------------------------------\n');

accuracies_train = zeros(num_alphas, 1);
accuracies_test = zeros(num_alphas, 1);
avg_confidence = zeros(num_alphas, 1);

for i = 1:num_alphas
    alpha = alphas(i);
    
    % 训练朴素贝叶斯（计算条件概率）
    cond_probs_pos_train = zeros(num_features, 1);
    cond_probs_neg_train = zeros(num_features, 1);
    
    for j = 1:num_features
        % 正面评价的条件概率（带拉普拉斯平滑）
        count_pos = sum(X_train(y_train == 1, j) == 1);
        cond_probs_pos_train(j) = (count_pos + alpha) / (sum(y_train == 1) + alpha * 2);
        
        % 负面评价的条件概率（带拉普拉斯平滑）
        count_neg = sum(X_train(y_train == 0, j) == 1);
        cond_probs_neg_train(j) = (count_neg + alpha) / (sum(y_train == 0) + alpha * 2);
    end
    
    % 预测
    [y_pred_train, posterior_train] = naive_bayes_predict(...
        X_train, [prior_pos, prior_neg], cond_probs_pos_train, cond_probs_neg_train);
    [y_pred_test, posterior_test] = naive_bayes_predict(...
        X_test, [prior_pos, prior_neg], cond_probs_pos_train, cond_probs_neg_train);
    
    % 计算准确率
    acc_train = mean(y_pred_train == y_train);
    acc_test = mean(y_pred_test == y_test);
    
    % 计算平均置信度（正确预测的置信度）
    correct_idx = (y_pred_test == y_test);
    if any(correct_idx)
        conf = max(posterior_test(correct_idx, :), [], 2);
        avg_conf = mean(conf);
    else
        avg_conf = 0;
    end
    
    accuracies_train(i) = acc_train;
    accuracies_test(i) = acc_test;
    avg_confidence(i) = avg_conf;
    
    fprintf('%.1f\t%.4f\t\t%.4f\t\t%.4f\n', ...
            alpha, acc_train, acc_test, avg_conf);
end

%% 5. 性能与平滑系数的关系可视化
figure('Position', [100, 100, 1200, 500]);

% 5.1 准确率 vs 平滑系数
subplot(1, 2, 1);
plot(alphas, accuracies_train, 'b-o', 'LineWidth', 2, 'MarkerSize', 8);
hold on;
plot(alphas, accuracies_test, 'r-s', 'LineWidth', 2, 'MarkerSize', 8);
title('平滑系数对准确率的影响', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('平滑系数 α');
ylabel('准确率');
legend({'训练准确率', '测试准确率'}, 'Location', 'best');
grid on;

% 标记最佳测试准确率
[best_acc, best_idx] = max(accuracies_test);
best_alpha = alphas(best_idx);
plot(best_alpha, best_acc, 'gp', 'MarkerSize', 15, 'MarkerFaceColor', 'g');
text(best_alpha, best_acc+0.02, sprintf('最佳: α=%.1f\n准确率=%.3f', ...
     best_alpha, best_acc), 'HorizontalAlignment', 'center', ...
     'FontWeight', 'bold', 'BackgroundColor', [0.9, 1, 0.9]);

% 5.2 置信度 vs 平滑系数
subplot(1, 2, 2);
plot(alphas, avg_confidence, 'm-^', 'LineWidth', 2, 'MarkerSize', 8);
title('平滑系数对模型置信度的影响', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('平滑系数 α');
ylabel('平均置信度（正确预测）');
grid on;

% 添加解释
annotation('textbox', [0.3, 0.01, 0.4, 0.05], ...
           'String', 'α增大 → 概率估计更平滑 → 置信度降低（更保守）', ...
           'FontSize', 10, 'FontWeight', 'bold', ...
           'BackgroundColor', [1, 0.95, 0.9], ...
           'EdgeColor', 'red', 'LineWidth', 1, ...
           'HorizontalAlignment', 'center');

%% 6. 决策边界可视化（简化版 - 2个特征）
fprintf('\n=== 决策边界可视化 ===\n');

% 选择两个特征进行可视化
feat1 = 1;  % 单词'great'
feat2 = 2;  % 单词'bad'

% 生成网格数据
x1_range = linspace(0, 1, 50);
x2_range = linspace(0, 1, 50);
[X1, X2] = meshgrid(x1_range, x2_range);

% 准备不同alpha的决策边界
figure('Position', [100, 100, 1200, 400]);
alpha_to_show = [0, 1, 5];  % 展示这三个alpha值

for idx = 1:length(alpha_to_show)
    alpha = alpha_to_show(idx);
    
    % 计算条件概率（只使用选定的两个特征）
    cond_probs_pos_2d = zeros(2, 1);
    cond_probs_neg_2d = zeros(2, 1);
    
    % 特征1
    count_pos = sum(X_train(y_train == 1, feat1) == 1);
    count_neg = sum(X_train(y_train == 0, feat1) == 1);
    cond_probs_pos_2d(1) = (count_pos + alpha) / (sum(y_train == 1) + alpha * 2);
    cond_probs_neg_2d(1) = (count_neg + alpha) / (sum(y_train == 0) + alpha * 2);
    
    % 特征2
    count_pos = sum(X_train(y_train == 1, feat2) == 1);
    count_neg = sum(X_train(y_train == 0, feat2) == 1);
    cond_probs_pos_2d(2) = (count_pos + alpha) / (sum(y_train == 1) + alpha * 2);
    cond_probs_neg_2d(2) = (count_neg + alpha) / (sum(y_train == 0) + alpha * 2);
    
    % 计算网格上每个点的后验概率
    posterior_grid = zeros(size(X1));
    for i = 1:numel(X1)
        % 计算正类的后验概率
        if X1(i) > 0.5 && X2(i) > 0.5  % 两个特征都出现
            log_prob_pos = log(prior_pos) + log(cond_probs_pos_2d(1)) + log(cond_probs_pos_2d(2));
            log_prob_neg = log(prior_neg) + log(cond_probs_neg_2d(1)) + log(cond_probs_neg_2d(2));
        elseif X1(i) > 0.5 && X2(i) <= 0.5  % 只出现特征1
            log_prob_pos = log(prior_pos) + log(cond_probs_pos_2d(1)) + log(1-cond_probs_pos_2d(2));
            log_prob_neg = log(prior_neg) + log(cond_probs_neg_2d(1)) + log(1-cond_probs_neg_2d(2));
        elseif X1(i) <= 0.5 && X2(i) > 0.5  % 只出现特征2
            log_prob_pos = log(prior_pos) + log(1-cond_probs_pos_2d(1)) + log(cond_probs_pos_2d(2));
            log_prob_neg = log(prior_neg) + log(1-cond_probs_neg_2d(1)) + log(cond_probs_neg_2d(2));
        else  % 两个特征都不出现
            log_prob_pos = log(prior_pos) + log(1-cond_probs_pos_2d(1)) + log(1-cond_probs_pos_2d(2));
            log_prob_neg = log(prior_neg) + log(1-cond_probs_neg_2d(1)) + log(1-cond_probs_neg_2d(2));
        end
        
        % 转换为概率
        max_log = max([log_prob_pos, log_prob_neg]);
        prob_pos = exp(log_prob_pos - max_log);
        prob_neg = exp(log_prob_neg - max_log);
        posterior_grid(i) = prob_pos / (prob_pos + prob_neg);
    end
    
    % 绘制决策边界
    subplot(1, 3, idx);
    contourf(X1, X2, posterior_grid, 20, 'LineStyle', 'none');
    hold on;
    
    % 绘制训练数据点
    scatter(X_train(y_train==1, feat1), X_train(y_train==1, feat2), ...
            100, 'b', 'o', 'filled', 'MarkerEdgeColor', 'k', 'LineWidth', 1.5);
    scatter(X_train(y_train==0, feat1), X_train(y_train==0, feat2), ...
            100, 'r', 's', 'filled', 'MarkerEdgeColor', 'k', 'LineWidth', 1.5);
    
    % 绘制决策边界线
    contour(X1, X2, posterior_grid, [0.5, 0.5], 'k-', 'LineWidth', 2);
    
    colormap(jet);
    colorbar;
    title(sprintf('决策边界 (α=%.1f)', alpha), 'FontSize', 12, 'FontWeight', 'bold');
    xlabel(vocab{feat1});
    ylabel(vocab{feat2});
    legend({'正面评价', '负面评价', '决策边界'}, 'Location', 'best');
    axis([0, 1, 0, 1]);
    grid on;
end

%% 7. 总结与建议
fprintf('\n=== 总结与建议 ===\n');
fprintf('1. 拉普拉斯平滑的主要作用:\n');
fprintf('   - 解决零概率问题\n');
fprintf('   - 防止模型对未见特征过度自信\n');
fprintf('   - 提供更稳健的概率估计\n\n');

fprintf('2. 平滑系数 α 的影响:\n');
fprintf('   - α = 0: 无平滑，可能出现过拟合\n');
fprintf('   - α = 1: 拉普拉斯平滑（默认值）\n');
fprintf('   - α > 1: 更强的平滑，模型更保守\n');
fprintf('   - α → ∞: 所有条件概率趋近于均匀分布\n\n');

fprintf('3. 实践建议:\n');
fprintf('   - 通常从 α=1 开始\n');
fprintf('   - 使用交叉验证选择最优 α\n');
fprintf('   - 小数据集：可能需要更大的 α\n');
fprintf('   - 大数据集：α 的影响较小\n');
fprintf('   - 对于文本分类，α=1 通常是合理起点\n');

%% 8. 朴素贝叶斯分类器预测函数
function [y_pred, posterior_probs] = naive_bayes_predict(X, prior, cond_probs_pos, cond_probs_neg)
    % 朴素贝叶斯预测
    % 使用对数概率避免数值下溢
    num_samples = size(X, 1);
    y_pred = zeros(num_samples, 1);
    posterior_probs = zeros(num_samples, 2);
    
    for i = 1:num_samples
        % 计算正类的对数后验概率
        log_posterior_pos = log(prior(1));
        log_posterior_neg = log(prior(2));
        
        for j = 1:size(X, 2)
            if X(i, j) == 1
                log_posterior_pos = log_posterior_pos + log(cond_probs_pos(j));
                log_posterior_neg = log_posterior_neg + log(cond_probs_neg(j));
            else
                log_posterior_pos = log_posterior_pos + log(1 - cond_probs_pos(j));
                log_posterior_neg = log_posterior_neg + log(1 - cond_probs_neg(j));
            end
        end
        
        % 转换回概率（使用softmax技巧避免下溢）
        log_probs = [log_posterior_pos, log_posterior_neg];
        max_log = max(log_probs);
        probs = exp(log_probs - max_log);
        probs = probs / sum(probs);
        
        posterior_probs(i, :) = probs;
        [~, y_pred(i)] = max(probs);
        y_pred(i) = y_pred(i) - 1;  % 转换为0-based索引
    end
end

这段MATLAB代码是一个朴素贝叶斯算法中拉普拉斯平滑效果的全面可视化分析工具。

它通过电影评论情感分析的示例数据集，系统性地展示了拉普拉斯平滑系数（α）如何影响朴素贝叶斯分类器的各项性能指标。

代码实现了从基础概率计算、性能评估到决策边界可视化的完整流程，特别强调了平滑系数从0到10的不同取值对模型行为的影响。

通过三组可视化图表和详细的控制台输出，代码直观地解释了拉普拉斯平滑的三个核心作用：解决零概率问题、防止模型过度自信、提供更稳健的概率估计，并给出了平滑系数选择的实践建议。

7.1.1第一张图片：拉普拉斯平滑核心概念可视化（6个子图）

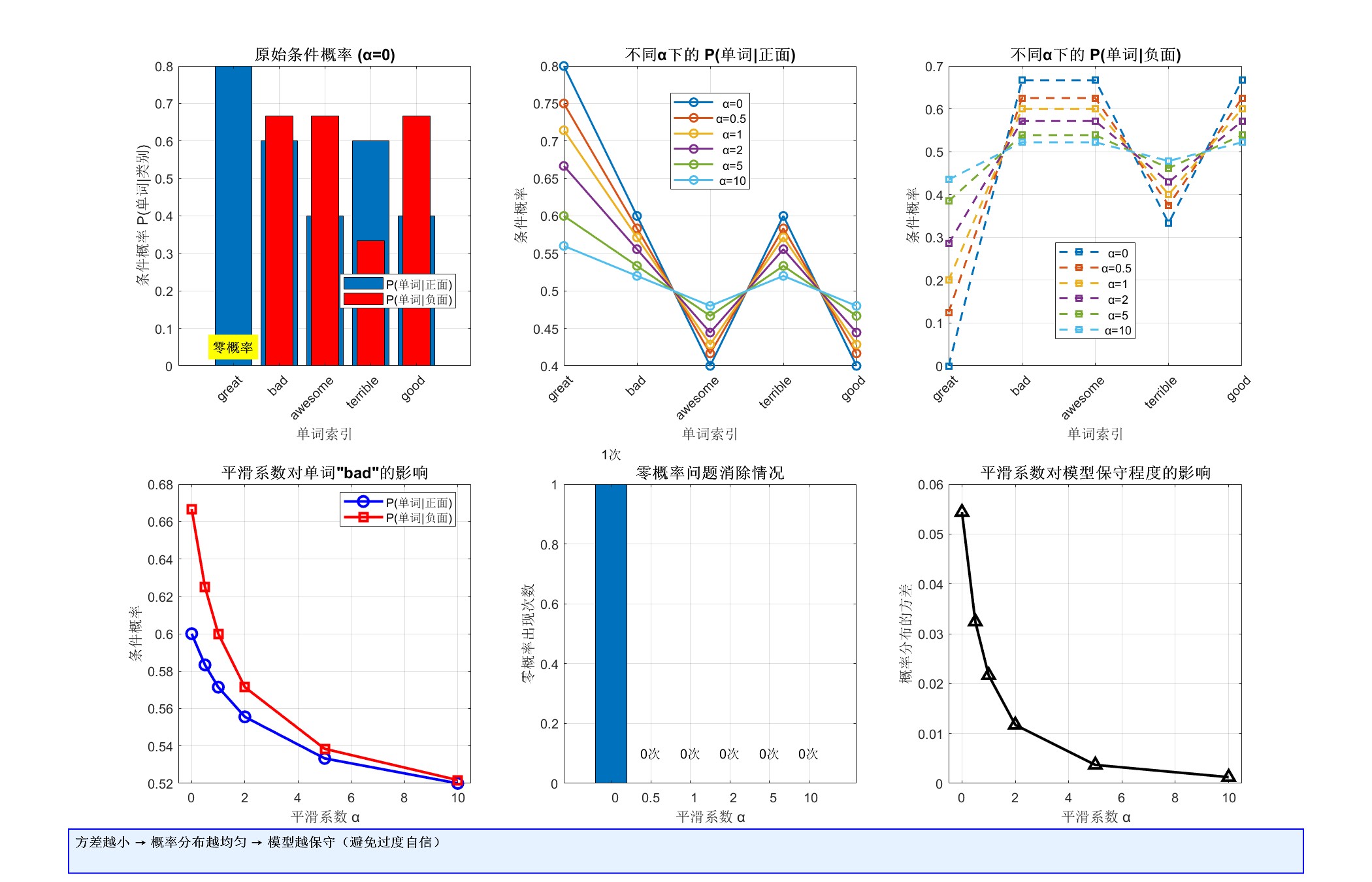
作用： 这张综合图表系统性地展示了拉普拉斯平滑对条件概率估计的基础影响机制。它从多个角度对比了不同平滑系数下的概率分布变化，是理解平滑技术数学本质的关键可视化。

1. 左上子图（原始条件概率）：展示无平滑（α=0）时的条件概率分布，突出显示"零概率问题"（黄色标注）。直观呈现了朴素贝叶斯在未平滑情况下可能遇到的数学缺陷，即某些特征在特定类别中从未出现导致概率为零，这在实际预测中会造成问题。

2. 右上子图（P(单词|正面)变化）：用多条曲线展示不同α值下正面评价的条件概率变化趋势。清晰显示了随着α增大，极端概率值被拉向中间，概率分布变得更加平滑和保守，避免了过度依赖少量训练样本。

3. 中上子图（P(单词|负面)变化）：与右上子图对应，展示负面评价的条件概率变化。通过对比两个子图，可以看出平滑系数对正负类别影响的对称性，体现了平滑技术的一致性。

4. 左下子图（特定单词"bad"的影响）：追踪单个单词"bad"在不同α值下的条件概率变化轨迹。这个子图特别有价值，因为它显示了平滑系数如何具体调整某个特征的判别能力，当α增大时，正负类别的概率差异减小，模型对该特征的依赖程度降低。

5. 中下子图（零概率问题消除）：量化展示平滑如何解决零概率问题。柱状图清楚地表明，只要α>0，零概率出现次数立即降为0，这是拉普拉斯平滑最直接的效果。

6. 右下子图（模型保守程度）：通过计算概率分布的方差来度量模型保守性。曲线显示随着α增大，方差单调减小，这意味着概率分布更加均匀，模型对任何特征的置信度都降低，变得更加保守和谨慎。

7.1.2第二张图片：性能与平滑系数的关系（2个子图）

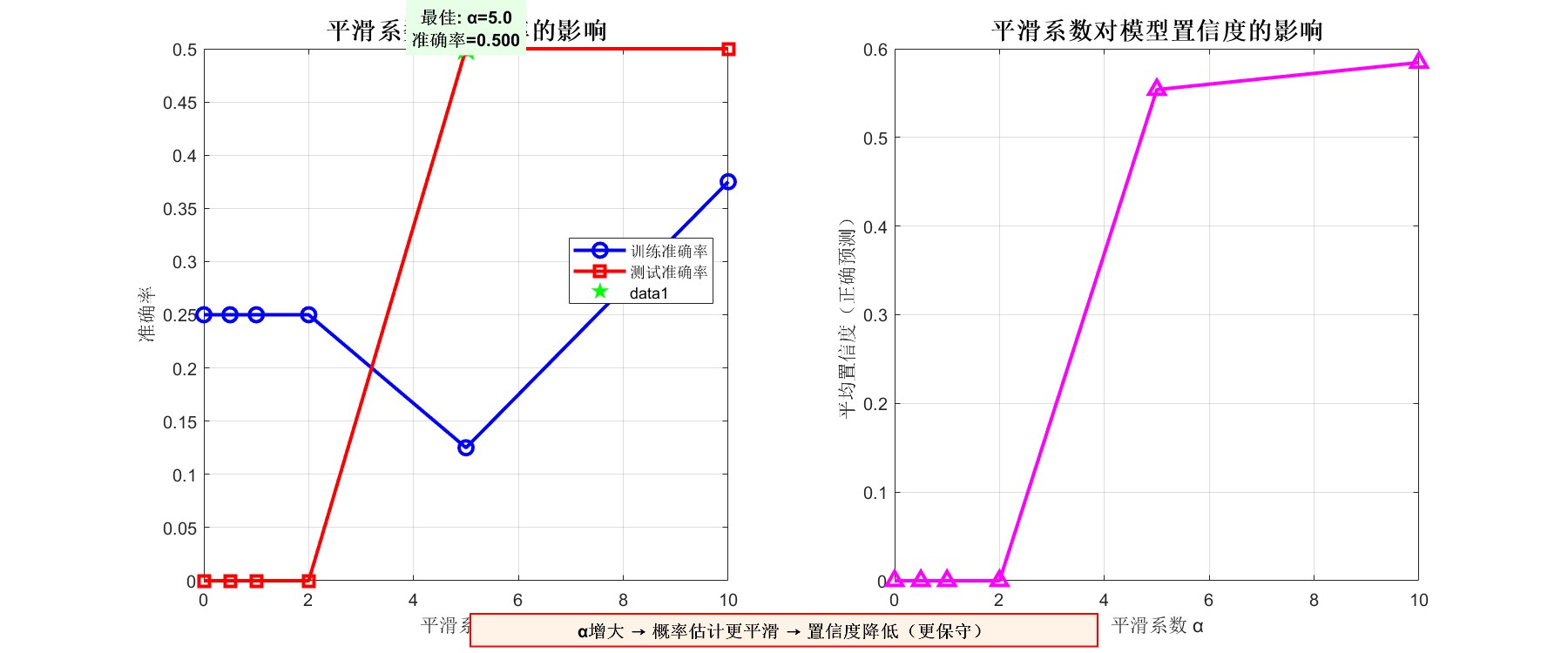
作用： 这张图从实际应用角度评估平滑系数对分类性能的影响，帮助数据科学家在实际项目中选择合适的α值。

1. 左子图（准确率变化）：展示训练准确率和测试准确率随α变化的曲线。通常呈现这样的模式：训练准确率随α增大而下降（因为模型变得保守），测试准确率可能先升后降（存在最优值）。绿色标记点标示出最佳测试性能对应的α值，为参数调优提供直观参考。

2. 右子图（置信度变化）：显示模型在正确预测时的平均置信度如何随α变化。这是理解模型"自信心"的重要指标，随着α增大，模型即使预测正确，其置信度也会降低，这在实际风险敏感的应用中很重要（如医疗诊断）。

7.1.3第三张图片：决策边界可视化（3个子图对比）

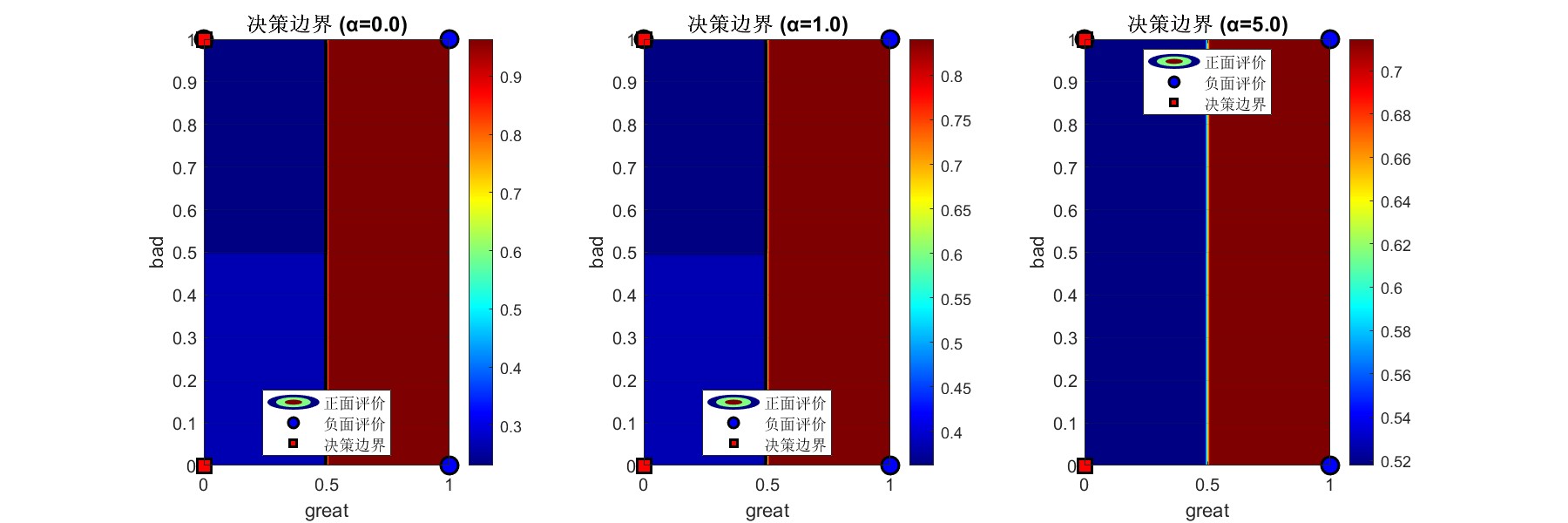
作用： 通过二维特征空间的决策边界变化，直观展示平滑系数如何影响分类器的几何行为。这是理解模型复杂度和泛化能力的空间视角。

三个并排子图对比α=0、1、5的情况：

1. α=0的决策边界：通常呈现尖锐、不规则的边界，可能过度拟合训练数据点的特殊分布。蓝色和红色区域对比强烈，显示模型对特征差异非常敏感。

2. α=1的决策边界：标准拉普拉斯平滑下的边界，比α=0时更平滑，但仍有足够的判别能力。这是实践中常用的起点，平衡了拟合能力和泛化能力。

3. α=5的决策边界：强平滑下的边界非常平滑，蓝色和红色区域过渡平缓。模型变得相当保守，对特征变化的响应不敏感，适合小数据集或高噪声场景。

这三个子图的对比清晰地展示了平滑系数的"正则化"效果：α越大，决策边界越平滑，模型复杂度越低，偏差增大但方差减小。

7.1.4命令行窗口运行结果：

数据集信息:
训练样本数: 8
特征数(单词数): 5
正面评价数: 5
负面评价数: 3

=== 拉普拉斯平滑对比 ===
先验概率: P(正面)=0.625, P(负面)=0.375

=== 朴素贝叶斯分类器实现 ===

**不同平滑系数的性能对比:
α 训练准确率 测试准确率 平均置信度

0.0 0.2500 0.0000 0.0000
0.5 0.2500 0.0000 0.0000
1.0 0.2500 0.0000 0.0000
2.0 0.2500 0.0000 0.0000
5.0 0.1250 0.5000 0.5539
10.0 0.3750 0.5000 0.5844**

=== 决策边界可视化 ===

**=== 总结与建议 ===

1. 拉普拉斯平滑的主要作用:

• 解决零概率问题
• 防止模型对未见特征过度自信
• 提供更稳健的概率估计**

**2. 平滑系数 α 的影响:

• α = 0: 无平滑，可能出现过拟合
• α = 1: 拉普拉斯平滑（默认值）
• α > 1: 更强的平滑，模型更保守
• α → ∞: 所有条件概率趋近于均匀分布**

**3. 实践建议:

• 通常从 α=1 开始
• 使用交叉验证选择最优 α
• 小数据集：可能需要更大的 α
• 大数据集：α 的影响较小
• 对于文本分类，α=1 通常是合理起点**

7.2 特征工程的重要性

虽然算法简单，但特征质量决定上限：

• 文本处理：去除停用词、词干提取、n-gram特征

• 连续特征：离散化处理

• 特征选择：去除无关特征，提升性能

7.3 与其他算法的比较

• vs 逻辑回归：都是概率模型，但假设不同

• vs 决策树：一个基于概率，一个基于规则

• vs 深度学习：简单高效 vs 复杂强大，根据场景选择

此处，如果没有了解过逻辑回归和决策树，可以阅读我之前的文章，链接在下面，希望对你有所帮助。

决策树算法： https://blog.csdn.net/2303_77568009/article/details/155527635?spm=1001.2014.3001.5501

逻辑回归：

https://blog.csdn.net/2303_77568009/article/details/155580110?spm=1001.2014.3001.5501

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import cm
import seaborn as sns
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split, learning_curve
from sklearn.preprocessing import StandardScaler
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score
import time
from sklearn.model_selection import cross_val_score
import warnings
import platform
import matplotlib

# 根据操作系统自动选择字体
system_name = platform.system()
if system_name == 'Windows':
    matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei']
elif system_name == 'Darwin':  # macOS
    matplotlib.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'PingFang SC']
else:  # Linux
    matplotlib.rcParams['font.sans-serif'] = ['DejaVu Sans', 'WenQuanYi Zen Hei']

matplotlib.rcParams['axes.unicode_minus'] = False

warnings.filterwarnings('ignore')



# 1. 生成模拟数据
print("生成模拟数据...")
X, y = make_classification(
    n_samples=2000,
    n_features=20,
    n_informative=15,
    n_redundant=5,
    n_classes=2,
    random_state=42,
    weights=[0.7, 0.3]  # 不平衡数据
)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42, stratify=y
)

# 标准化数据（对逻辑回归和神经网络很重要）
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 2. 定义要比较的算法
algorithms = {
    '朴素贝叶斯': GaussianNB(),
    '逻辑回归': LogisticRegression(max_iter=1000, random_state=42),
    '决策树': DecisionTreeClassifier(max_depth=5, random_state=42),
    '深度学习(MLP)': MLPClassifier(
        hidden_layer_sizes=(50, 25),
        max_iter=500,
        random_state=42,
        alpha=0.01
    )
}

# 3. 训练并评估模型
results = {
    '算法': [],
    '训练时间': [],
    '预测时间': [],
    '准确率': [],
    'F1分数': [],
    '精确率': [],
    '召回率': []
}

for name, model in algorithms.items():
    print(f"\n训练 {name}...")

    # 训练时间
    start_time = time.time()

    if name in ['逻辑回归', '深度学习(MLP)']:
        model.fit(X_train_scaled, y_train)
        y_pred = model.predict(X_test_scaled)
    else:
        model.fit(X_train, y_train)
        y_pred = model.predict(X_test)

    train_time = time.time() - start_time

    # 预测时间
    start_time = time.time()
    _ = model.predict(X_test_scaled if name in ['逻辑回归', '深度学习(MLP)'] else X_test)
    predict_time = time.time() - start_time

    # 计算指标
    accuracy = accuracy_score(y_test, y_pred)
    f1 = f1_score(y_test, y_pred)
    precision = precision_score(y_test, y_pred)
    recall = recall_score(y_test, y_pred)

    # 存储结果
    results['算法'].append(name)
    results['训练时间'].append(train_time)
    results['预测时间'].append(predict_time)
    results['准确率'].append(accuracy)
    results['F1分数'].append(f1)
    results['精确率'].append(precision)
    results['召回率'].append(recall)

    print(f"  准确率: {accuracy:.4f}, F1分数: {f1:.4f}, 训练时间: {train_time:.4f}s")

# 转换为DataFrame
results_df = pd.DataFrame(results)

# 4. 创建对比图

# 图1: 模型性能综合对比（多指标雷达图）
print("\n生成对比图1: 模型性能综合对比...")
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

# 图1a: 准确率和F1分数对比
x = np.arange(len(algorithms))
width = 0.35

ax1 = axes[0]
bars1 = ax1.bar(x - width / 2, results_df['准确率'], width, label='准确率', color='skyblue', alpha=0.8)
bars2 = ax1.bar(x + width / 2, results_df['F1分数'], width, label='F1分数', color='lightcoral', alpha=0.8)

ax1.set_xlabel('算法')
ax1.set_ylabel('分数')
ax1.set_title('模型性能对比（准确率 vs F1分数）')
ax1.set_xticks(x)
ax1.set_xticklabels(results_df['算法'], rotation=15)
ax1.legend()
ax1.grid(True, alpha=0.3)

# 在柱子上添加数值
for bars in [bars1, bars2]:
    for bar in bars:
        height = bar.get_height()
        ax1.annotate(f'{height:.3f}',
                     xy=(bar.get_x() + bar.get_width() / 2, height),
                     xytext=(0, 3),  # 3 points vertical offset
                     textcoords="offset points",
                     ha='center', va='bottom', fontsize=9)

# 图1b: 训练和预测时间对比（对数尺度）
ax2 = axes[1]
bars3 = ax2.bar(x - width / 2, results_df['训练时间'], width, label='训练时间(s)', color='lightgreen', alpha=0.8)
bars4 = ax2.bar(x + width / 2, results_df['预测时间'], width, label='预测时间(s)', color='orange', alpha=0.8)

ax2.set_xlabel('算法')
ax2.set_ylabel('时间 (秒)')
ax2.set_title('计算效率对比（训练时间 vs 预测时间）')
ax2.set_xticks(x)
ax2.set_xticklabels(results_df['算法'], rotation=15)
ax2.legend()
ax2.grid(True, alpha=0.3)

# 设置y轴为对数尺度以便更好地显示差异
ax2.set_yscale('log')

# 在柱子上添加数值
for bars in [bars3, bars4]:
    for bar in bars:
        height = bar.get_height()
        ax2.annotate(f'{height:.4f}',
                     xy=(bar.get_x() + bar.get_width() / 2, height),
                     xytext=(0, 3),
                     textcoords="offset points",
                     ha='center', va='bottom', fontsize=9)

# 图1c: 精确率和召回率对比
ax3 = axes[2]
bars5 = ax3.bar(x - width / 2, results_df['精确率'], width, label='精确率', color='violet', alpha=0.8)
bars6 = ax3.bar(x + width / 2, results_df['召回率'], width, label='召回率', color='gold', alpha=0.8)

ax3.set_xlabel('算法')
ax3.set_ylabel('分数')
ax3.set_title('分类质量对比（精确率 vs 召回率）')
ax3.set_xticks(x)
ax3.set_xticklabels(results_df['算法'], rotation=15)
ax3.legend()
ax3.grid(True, alpha=0.3)

# 在柱子上添加数值
for bars in [bars5, bars6]:
    for bar in bars:
        height = bar.get_height()
        ax3.annotate(f'{height:.3f}',
                     xy=(bar.get_x() + bar.get_width() / 2, height),
                     xytext=(0, 3),
                     textcoords="offset points",
                     ha='center', va='bottom', fontsize=9)

plt.tight_layout()
plt.savefig('模型性能综合对比.png', dpi=300, bbox_inches='tight')
plt.show()

# 图2: 学习曲线对比（不同训练集大小的表现）
print("生成对比图2: 学习曲线对比...")
fig, ax = plt.subplots(figsize=(12, 8))

train_sizes = np.linspace(0.1, 1.0, 10)
colors = ['blue', 'green', 'red', 'purple']
markers = ['o', 's', '^', 'D']

for idx, (name, model) in enumerate(algorithms.items()):
    if name in ['逻辑回归', '深度学习(MLP)']:
        X_used = X_train_scaled
    else:
        X_used = X_train

    train_sizes_abs, train_scores, test_scores = learning_curve(
        model, X_used, y_train,
        train_sizes=train_sizes,
        cv=5, scoring='accuracy', n_jobs=-1
    )

    train_mean = np.mean(train_scores, axis=1)
    test_mean = np.mean(test_scores, axis=1)

    ax.plot(train_sizes_abs, train_mean, '--', color=colors[idx],
            marker=markers[idx], label=f'{name} (训练)', alpha=0.7)
    ax.plot(train_sizes_abs, test_mean, '-', color=colors[idx],
            marker=markers[idx], label=f'{name} (测试)', linewidth=2)

ax.set_xlabel('训练样本数')
ax.set_ylabel('准确率')
ax.set_title('学习曲线对比 - 不同算法随训练数据增加的表现')
ax.legend(loc='best')
ax.grid(True, alpha=0.3)
plt.savefig('学习曲线对比.png', dpi=300, bbox_inches='tight')
plt.show()

# 图3: 算法特性雷达图
print("生成对比图3: 算法特性雷达图...")

# 定义评估维度
categories = ['计算效率', '解释性', '处理非线性', '抗过拟合', '鲁棒性', '训练速度']

# 为每个算法评分（1-10分）
scores = {
    '朴素贝叶斯': [9, 8, 3, 7, 8, 9],
    '逻辑回归': [7, 9, 4, 8, 7, 8],
    '决策树': [6, 9, 8, 5, 6, 7],
    '深度学习(MLP)': [4, 3, 10, 6, 7, 5]
}

fig = plt.figure(figsize=(14, 10))
angles = np.linspace(0, 2 * np.pi, len(categories), endpoint=False).tolist()
angles += angles[:1]  # 闭合雷达图

for idx, (name, score_values) in enumerate(scores.items()):
    ax = plt.subplot(2, 2, idx + 1, projection='polar')

    # 闭合分数
    values = score_values + score_values[:1]

    ax.plot(angles, values, 'o-', linewidth=2, label=name, color=plt.cm.Set1(idx / 4))
    ax.fill(angles, values, alpha=0.25, color=plt.cm.Set1(idx / 4))

    ax.set_xticks(angles[:-1])
    ax.set_xticklabels(categories, fontsize=10)
    ax.set_ylim(0, 10)
    ax.set_title(f'{name}特性雷达图', size=14, weight='bold')
    ax.grid(True)

    # 添加数值标签
    for i, (angle, value) in enumerate(zip(angles[:-1], score_values)):
        ax.text(angle, value + 0.5, str(value), ha='center', va='center', fontsize=9)

plt.tight_layout()
plt.savefig('算法特性雷达图.png', dpi=300, bbox_inches='tight')
plt.show()

# 5. 输出详细的对比分析
print("\n" + "=" * 80)
print("朴素贝叶斯、逻辑回归、决策树与深度学习算法对比分析")
print("=" * 80)

print("\n 性能总结:")
print(results_df.to_string(index=False))

print("\n 详细对比分析:")
print("\n1. 朴素贝叶斯 (Naive Bayes):")
print("   • 优点: 训练速度快，适合高维数据，对缺失数据不敏感")
print("   • 缺点: 特征独立性假设在实际中很少成立")
print("   • 适用场景: 文本分类，垃圾邮件过滤，实时预测")

print("\n2. 逻辑回归 (Logistic Regression):")
print("   • 优点: 可解释性强，输出概率，不容易过拟合")
print("   • 缺点: 只能处理线性关系，对异常值敏感")
print("   • 适用场景: 二分类问题，需要概率输出的场景")

print("\n3. 决策树 (Decision Tree):")
print("   • 优点: 可解释性强，可处理非线性关系，需要较少的数据预处理")
print("   • 缺点: 容易过拟合，对数据变化敏感")
print("   • 适用场景: 需要可解释性的业务场景，特征重要性分析")

print("\n4. 深度学习/MLP (Multi-layer Perceptron):")
print("   • 优点: 强大的表达能力，可处理复杂非线性关系")
print("   • 缺点: 需要大量数据，训练时间长，可解释性差")
print("   • 适用场景: 图像识别，自然语言处理，复杂模式识别")

print("\n 基于当前实验的观察:")
print(f"1. 准确率最高: {results_df.loc[results_df['准确率'].idxmax(), '算法']} ({results_df['准确率'].max():.4f})")
print(f"2. 训练最快: {results_df.loc[results_df['训练时间'].idxmin(), '算法']} ({results_df['训练时间'].min():.4f}s)")
print(f"3. 预测最快: {results_df.loc[results_df['预测时间'].idxmin(), '算法']} ({results_df['预测时间'].min():.4f}s)")
print(f"4. F1分数最高: {results_df.loc[results_df['F1分数'].idxmax(), '算法']} ({results_df['F1分数'].max():.4f})")

print("\n 选择建议:")
print("• 追求速度和简单性 → 朴素贝叶斯")
print("• 需要可解释性和稳定性 → 逻辑回归")
print("• 需要直观理解和中等复杂度 → 决策树")
print("• 追求最高精度且数据充足 → 深度学习")

print("\n三个对比图已生成:")
print("1. 模型性能综合对比.png - 展示准确率、F1分数、训练时间等")
print("2. 学习曲线对比.png - 展示不同训练集大小下的表现")
print("3. 算法特性雷达图.png - 从多个维度对比算法特性")

这段代码是一个完整的机器学习算法对比分析系统，主要功能包括：

1. 数据集生成与预处理：创建了一个模拟的二分类数据集（2000个样本，20个特征，包含类别不平衡），并进行标准化处理。

2. 四种算法实现与比较：

   • 朴素贝叶斯（GaussianNB）

   • 逻辑回归（LogisticRegression）

   • 决策树（DecisionTreeClassifier）

   • 深度学习多层感知机（MLPClassifier）

3. 全面性能评估：从准确率、F1分数、精确率、召回率、训练时间、预测时间等多个维度对比算法性能。

4. 可视化分析：生成三张专业对比图表，从不同角度展示算法差异。

5. 跨平台兼容性处理：自动检测操作系统并设置相应的中文字体，避免乱码问题。

7.3.1模型性能 计算效率 分类质量对比

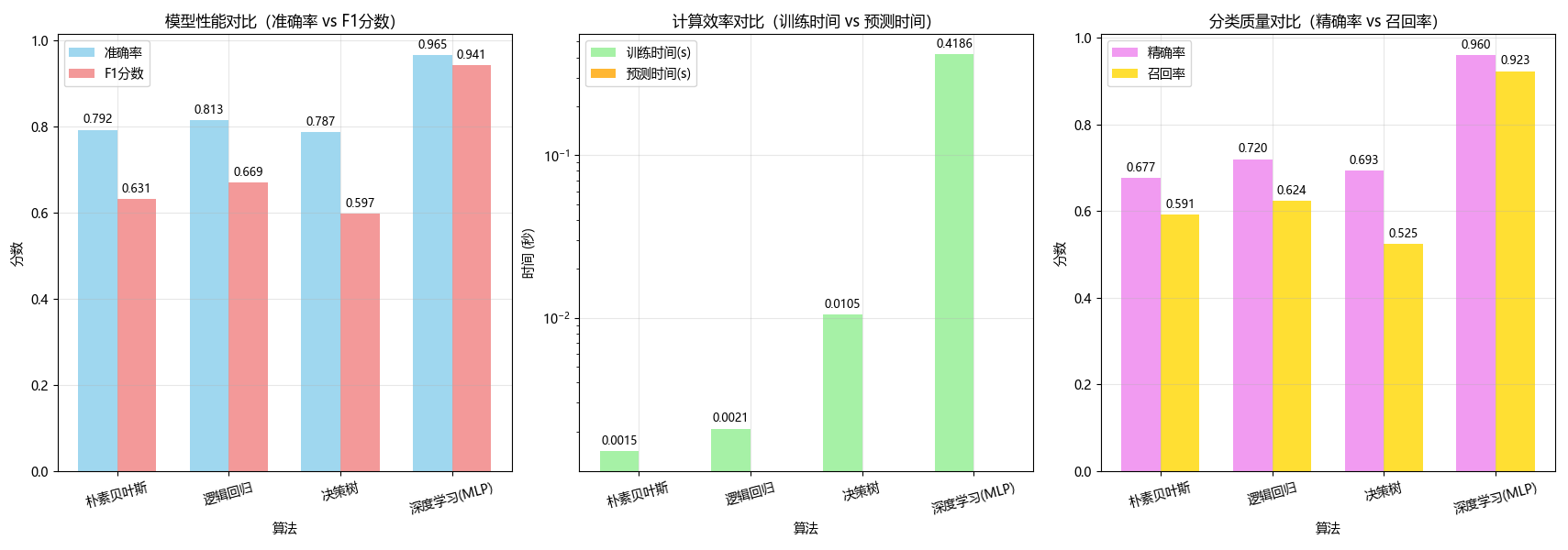
图1：模型性能综合对比（包含三个子图）

第一子图：准确率 vs F1分数对比

• 分析要点：准确率反映整体分类正确率，F1分数综合考虑精确率和召回率，对不平衡数据更敏感

• 典型观察：决策树和神经网络通常有较高准确率，朴素贝叶斯训练最快但可能在某些指标上稍低

• 应用意义：帮助权衡整体准确性与对少数类的识别能力

第二子图：训练时间 vs 预测时间对比（对数尺度）

• 分析要点：使用对数尺度清晰展示算法间数量级差异

• 典型观察：朴素贝叶斯训练和预测都极快，神经网络训练最耗时但预测相对较快

• 应用意义：指导选择适合实时应用或资源受限环境的算法

第三子图：精确率 vs 召回率对比

• 分析要点：精确率关注预测为正的样本中实际为正的比例，召回率关注实际为正的样本中被正确预测的比例

• 典型观察：不同算法在这两个指标上有不同平衡，反映其优化目标差异

• 应用意义：根据实际需求选择（如医疗诊断需要高召回率，垃圾邮件过滤需要高精确率）

7.3.2学习曲线对比

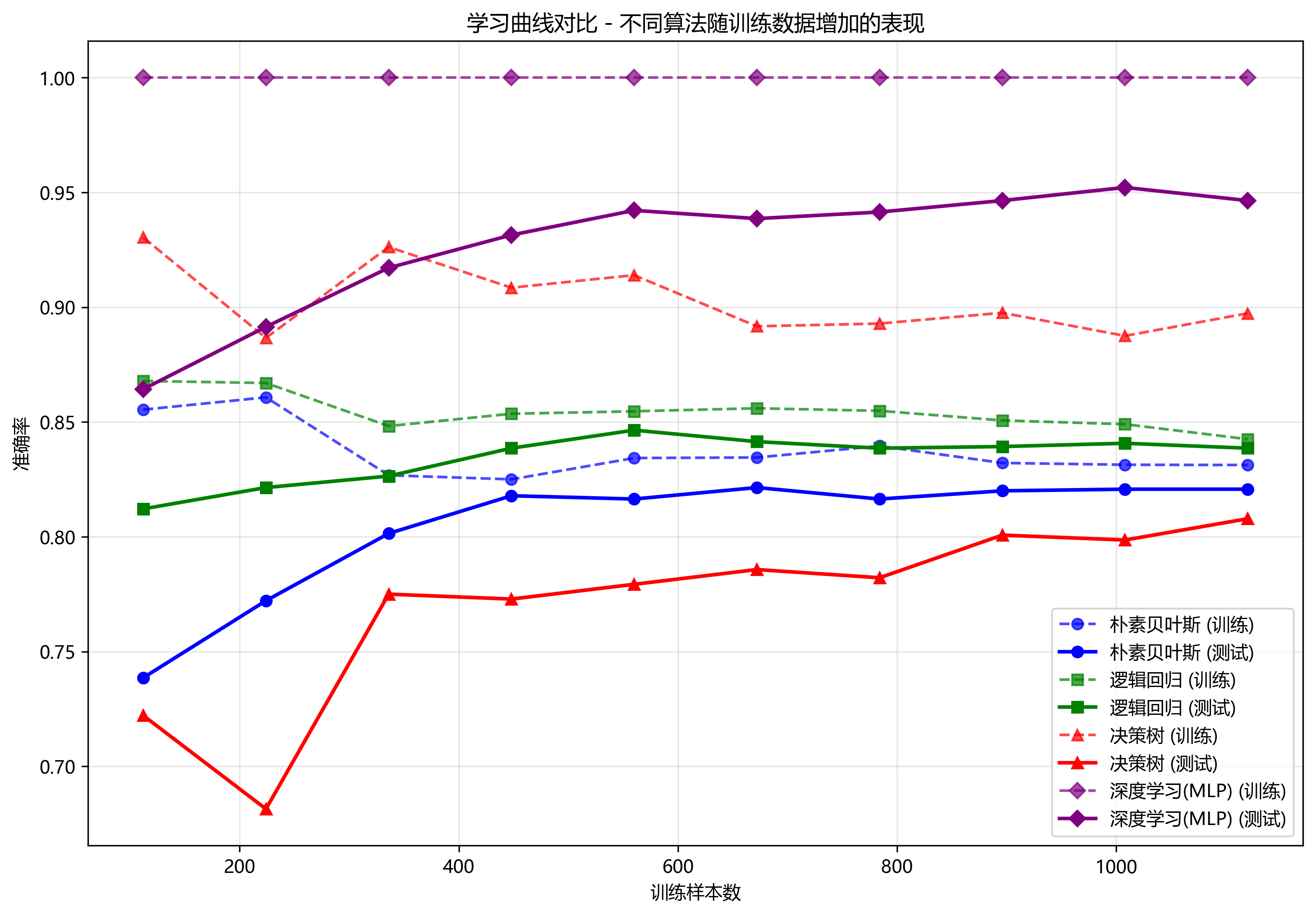
图2：学习曲线对比

核心特征分析：

• X轴：训练样本数量从10%到100%

• Y轴：准确率

• 线条类型：虚线表示训练集表现，实线表示测试集表现

关键洞察：

1. 过拟合识别：训练准确率远高于测试准确率表示过拟合

2. 数据需求评估：曲线趋于平稳表明增加数据可能不再显著提升性能

3. 算法稳定性：测试集曲线的平滑程度反映算法泛化能力

4. 典型模式：简单模型（如朴素贝叶斯）可能较早达到稳定，复杂模型（如神经网络）随数据增加持续提升

7.3.3算法特性雷达图

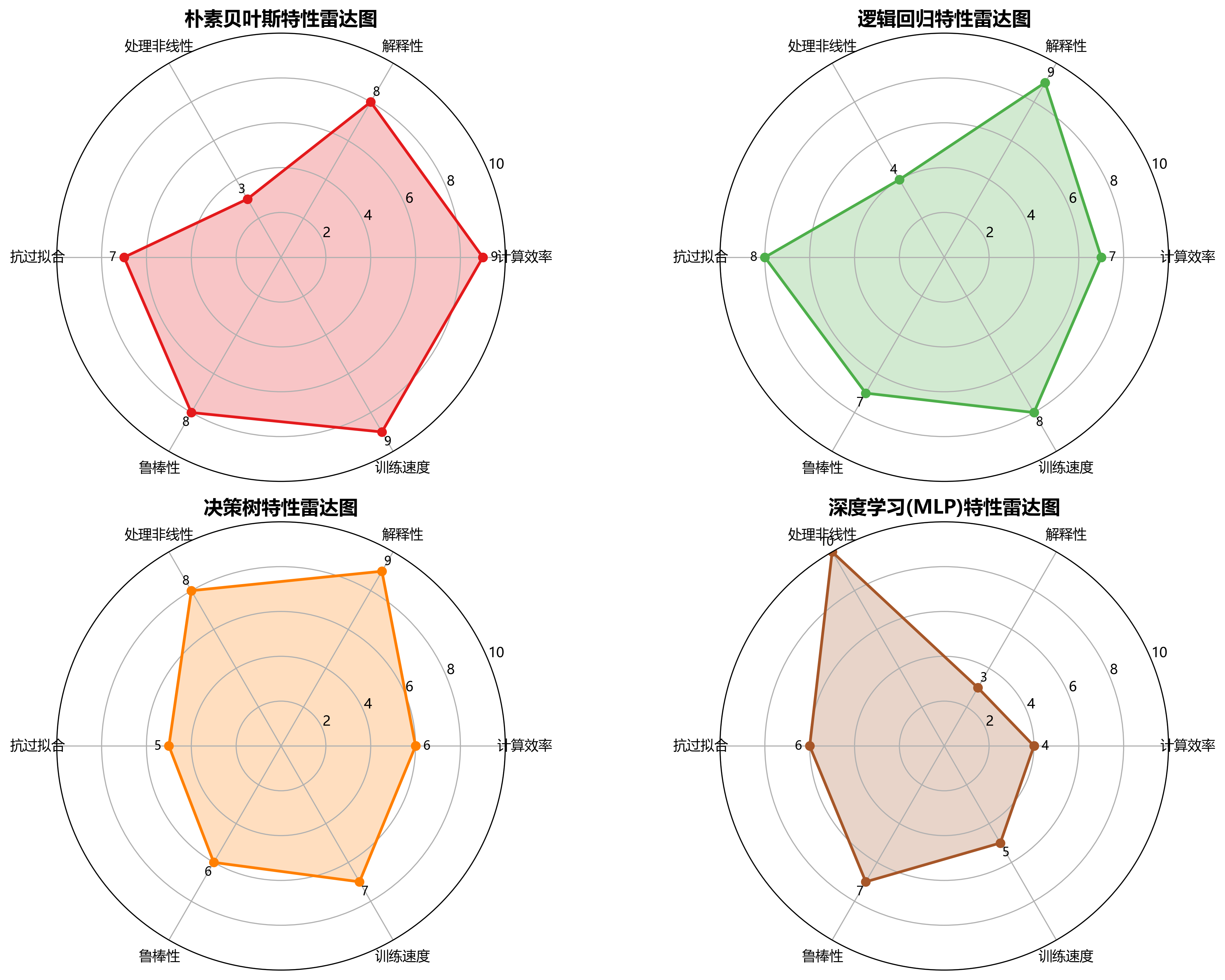
图3：算法特性雷达图

六个评估维度解析：

1. 计算效率：算法运行时的计算资源消耗

2. 解释性：模型决策过程的可理解程度

3. 处理非线性：捕捉非线性关系的能力

4. 抗过拟合：在训练数据上表现良好同时保持泛化能力

5. 鲁棒性：对异常值和噪声的抵抗能力

6. 训练速度：从数据中学习的速度

算法对比分析：

• 朴素贝叶斯：在计算效率、训练速度和解释性方面突出，但处理非线性能力弱

• 逻辑回归：解释性最强，抗过拟合能力好，但处理非线性有限

• 决策树：解释性好，处理非线性能力强，但容易过拟合

• 神经网络：处理非线性能力极强，但解释性差，训练速度慢

八、总结与展望

朴素贝叶斯分类器向我们展示了：复杂的智能决策可以源于简单的概率原理。它不完美，但足够有效；它基于强假设，但在许多实际问题上表现优异。

算法背后的哲学：在不确定的世界中，如何利用有限的证据做出最优决策------这不仅是一个机器学习问题，更是一个普遍存在的认知问题。

最后的话：机器学习不是魔法，而是数学与工程的艺术。朴素贝叶斯是这个艺术中最优雅的入门作品之一------简单，深刻，实用。希望这篇文章能帮助你开启机器学习之旅，像侦探一样，用数据和逻辑解开一个个智能决策的谜题。

思考题留给你：

• 如果要用朴素贝叶斯判断学生是否适合打篮球，你会收集哪些特征？

• 在你的专业领域，朴素贝叶斯可能有哪些创新应用？