283. 移动零
https://leetcode.cn/problems/move-zeroes/
给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
请注意 ，必须在不复制数组的情况下原地对数组进行操作。
python
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0⭐ 本题使用的是"双指针 · 同向指针（slow/fast）"
-
right 指针（fast）：遍历数组，寻找所有非零数字
-
left 指针（slow）：指向下一个应该放非零数字的位置
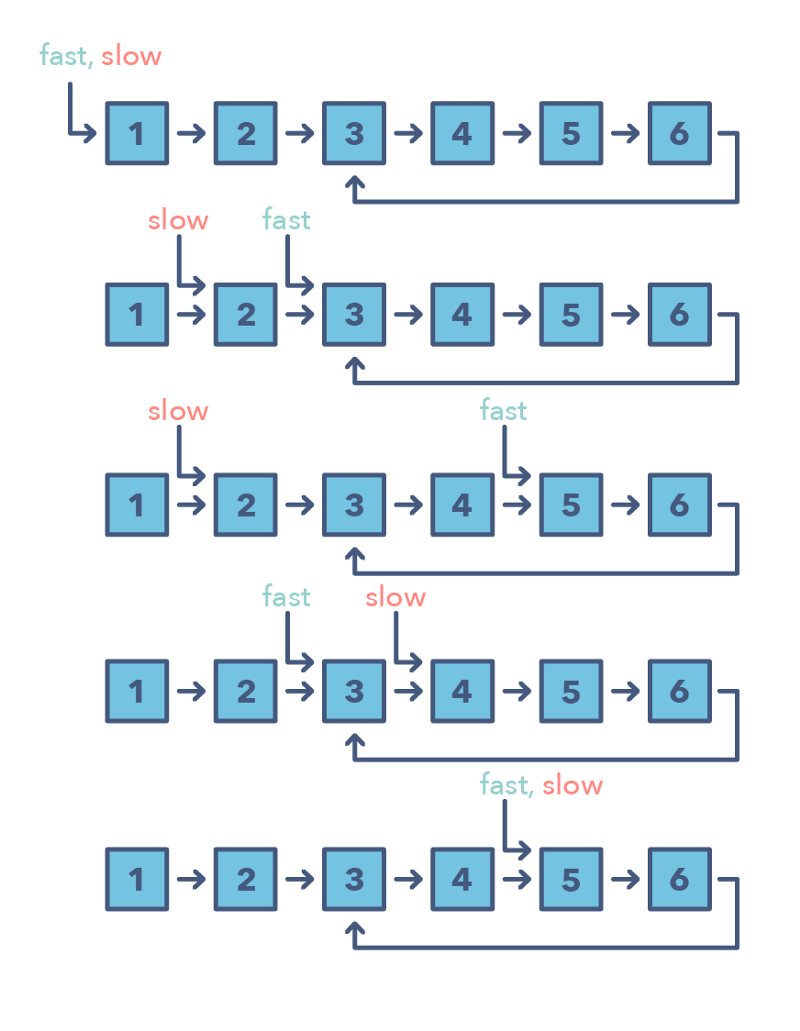
初始数组：
[0, 1, 0, 3, 12]
L
R
1️⃣ R=0，nums[0] = 0 → 不动
[0, 1, 0, 3, 12]
L
R
2️⃣ R=1，nums[1] = 1 → 和 L(=0) 交换
[1, 0, 0, 3, 12]
L
R
3️⃣ R=2，nums[2] = 0 → 不动
[1, 0, 0, 3, 12]
L
R
4️⃣ R=3，nums[3] = 3 → 与 L(=1) 交换
[1, 3, 0, 0, 12]
L
R
5️⃣ R=4，nums[4] = 12 → 与 L(=2) 交换
[1, 3, 12, 0, 0]
L
R
最终结果：
[1, 3, 12, 0, 0]python代码如下：
python
class Solution:
def moveZeroes(self, nums):
left, right = 0, 0
while right < len(nums):
if nums[right] != 0:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right += 111. 盛最多水的容器https://leetcode.cn/problems/container-with-most-water/
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和(i, heighti) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
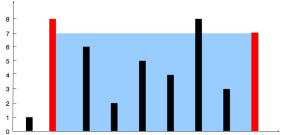
⭐ 本题使用的是"双指针 · 对撞指针"
1. 定义两个指针
left 指向最左边的木板（0） right 指向最右边的木板（n-1）
2. 当前这两块木板能装多少水？
python
width = right - left
height_container = min(height[left], height[right])
area = width * height_container用一个变量 max_area 记录最大值。
3. 关键问题：下一步应该动谁？
只有移动矮板，才可能出现更高的短板，增加面积
python
left = 0, right = n - 1, max_area = 0
当 left < right 时循环：
计算当前面积：
area = (right - left) * min(height[left], height[right])
更新 max_area
如果 height[left] < height[right]：
left += 1
否则：
right -= 1
循环结束，返回 max_areapython代码如下：
python
class Solution:
def maxArea(self, height):
left, right = 0, len(height) - 1
max_area = 0
while left < right:
# 当前容器宽度
width = right - left
# 短板高度
h = min(height[left], height[right])
# 当前面积
area = width * h
# 更新最大值
max_area = max(max_area, area)
# 谁矮谁挪窝
if height[left] < height[right]:
left += 1
else:
right -= 1
return max_area15. 三数之和https://leetcode.cn/problems/3sum/
给你一个整数数组 nums ，判断是否存在三元组 nums\[i, numsj, numsk] 满足 i != j、i != k 且 j != k ，同时还满足 numsi + numsj + numsk == 0 。请你返回所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。
python
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。⭐ 本题使用的是 排序+"双指针 · 对撞指针"
想象一个场景：
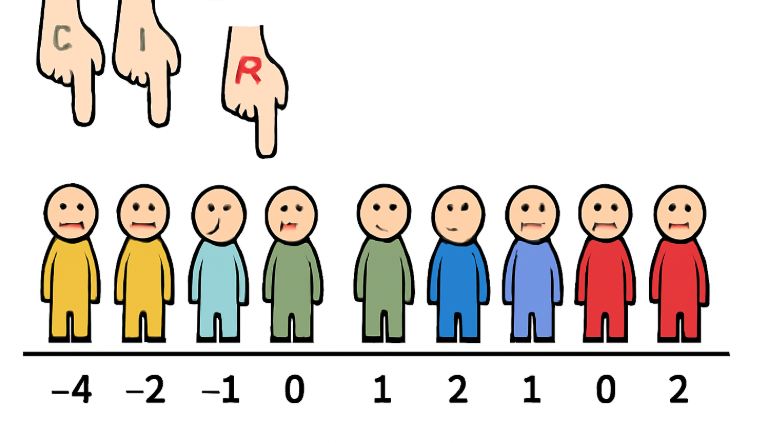
有一条队伍，队伍里站着很多同学，每个同学手里拿着一个"分数"，可能是负的，也可能是正的。
老师的任务是：
"在这堆同学里，找出所有 三人小组 ，
让他们手里的分数加起来 刚好等于 0 ，
而且 同样的三人组合不能算两次。"
-
先让同学按分数从小到大排好队（排序）
-
接着，老师做下面的事：
-
从左到右，一个一个选"第一个同学"当队长（下标 i）
-
然后在他右边，用两只手：
-
左手指向队长右边第一个人（left）
-
右手指向队伍最后一个人（right）
-
-
这三个同学（队长、left、right）的分数之和：
-
如果 太小了（<0） ：说明分数不够，需要更大一点
👉 左手往右挪一步（left++）
-
如果 太大了（>0） ：说明分数太大，需要小一点
👉 右手往左挪一步（right--）
-
如果 刚好等于 0 ：
👉 记录下这组三人组
👉 然后左右手都挪一格，继续找下一组
-
-
并且，老师还有一个要求："如果遇到 一模一样的分数的同学，同样的选法就不再重复试一遍（去重）。"
就这样，把原本需要三重循环才能做的事情，用两重循环就搞定了。
python代码如下：
python
class Solution:
def threeSum(self, nums):
nums.sort() # 1. 先排序
n = len(nums)
res = []
for i in range(n):
# 剪枝1：如果第一个数已经 > 0，后面更不可能凑成 0
if nums[i] > 0:
break
# 去重1：跳过相同的起点
if i > 0 and nums[i] == nums[i - 1]:
continue
left, right = i + 1, n - 1
while left < right:
s = nums[i] + nums[left] + nums[right]
if s < 0:
# 总和太小，左指针右移，让和变大
left += 1
elif s > 0:
# 总和太大，右指针左移，让和变小
right -= 1
else:
# 找到一个三元组
res.append([nums[i], nums[left], nums[right]])
# 去重2：跳过相同的 left
while left < right and nums[left] == nums[left + 1]:
left += 1
# 去重3：跳过相同的 right
while left < right and nums[right] == nums[right - 1]:
right -= 1
# 移动到下一对
left += 1
right -= 1
return res