周志华《机器学习—西瓜书》五

周志华《机器学习---西瓜书》五

五、支持向量机

5-1、支持向量机基本型

这组图片围绕支持向量机（SVM） 的核心概念展开，内容如下：

一、线性分类器回顾

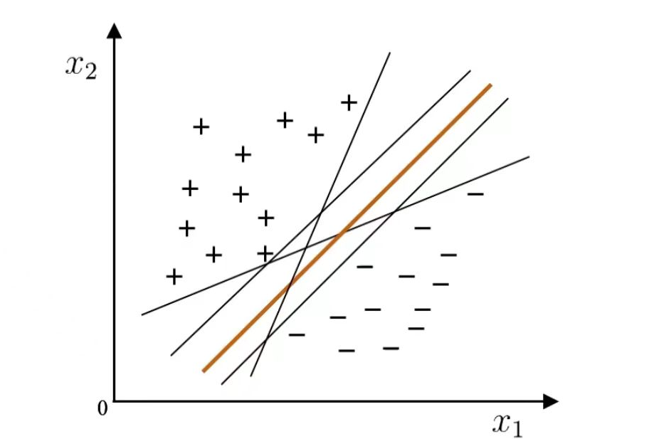
在线性可分的场景中，能将训练样本分开的超平面可能有多个。

问题：将训练样本分开的超平面可能有很多，哪一个更好呢？

其中"正中间"的超平面鲁棒性最好、泛化能力最强，这是支持向量机的核心思想之一。

二、间隔（Margin）与支持向量（Support Vector）

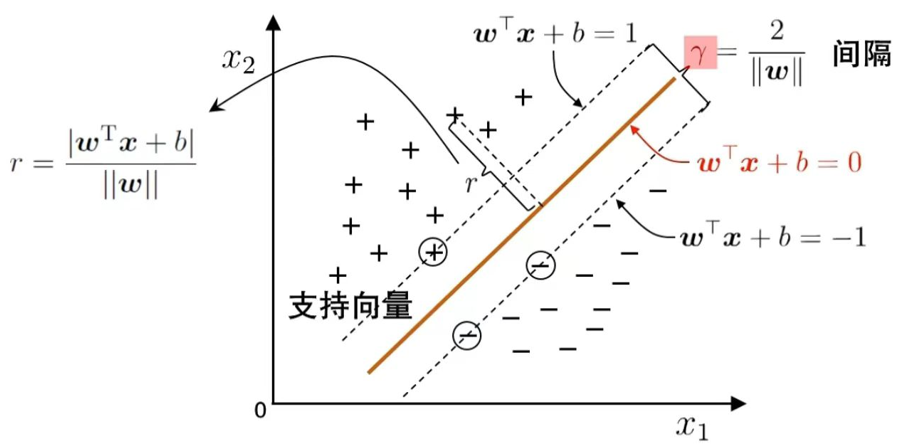
超平面方程：wTx+b=0{w}^\text{T}{x} + b = 0wTx+b=0
样本到超平面的距离公式：r=∣wTx+b∣∥w∥r = \frac{|{w}^\text{T}{x} + b|}{\|{w}\|}r=∥w∥∣wTx+b∣
间隔（Margin）：两个平行超平面（wTx+b=1{w}^\text{T}{x} + b = 1wTx+b=1 和 wTx+b=−1{w}^\text{T}{x} + b = -1wTx+b=−1）之间的距离，即 γ=2∥w∥\gamma = \frac{2}{\|{w}\|}γ=∥w∥2。
支持向量：两条虚线，恰好落在这两个平行超平面上的样本，是决定间隔大小的关键样本。

三、支持向量机基本型

目标是寻找参数 w{w}w 和 bbb，使得间隔 γ\gammaγ 最大，转化为优化问题：

原始最大化间隔的形式： "s.t." 是 subject to 的缩写，中文意思是 "受限于" 或 "满足...... 约束条件"

arg⁡max⁡w,b 2∥w∥s.t. yi(wTxi+b)≥1, i=1,2,...,m \underset{{w}, b}{\arg\max} \ \frac{2}{\|{w}\|} \quad \text{s.t.} \ y_i({w}^\text{T}{x}_i + b) \geq 1, \ i = 1,2,\dots,m w,bargmax ∥w∥2s.t. yi(wTxi+b)≥1, i=1,2,...,m
等价的最小化形式（通过数学变换，最大化 2∥w∥\frac{2}{\|{w}\|}∥w∥2 等价于最小化 12∥w∥2\frac{1}{2}\|{w}\|^221∥w∥2）：

arg⁡min⁡w,b 12∥w∥2s.t. yi(wTxi+b)≥1, i=1,2,...,m \underset{{w}, b}{\arg\min} \ \frac{1}{2}\|{w}\|^2 \quad \text{s.t.} \ y_i({w}^\text{T}{x}_i + b) \geq 1, \ i = 1,2,\dots,m w,bargmin 21∥w∥2s.t. yi(wTxi+b)≥1, i=1,2,...,m

这是一个凸二次规划问题，可通过优化计算包求解，也存在更高效的方法（如对偶问题、核技巧等）。

‍

核心变化：

原始目的是 最大化间隔 γ\gammaγ** === 2∥w∥\frac{2}{\|\boldsymbol{w}\|}∥w∥2** → 等价于 最小化 12∥w∥2\frac{1}{2}\|\boldsymbol{w}\|^221∥w∥2 （因为 γ\gammaγ 越大，∥w∥\|\boldsymbol{w}\|∥w∥ 越小）。

而对偶问题的 "最大化目标函数" ∑i=1mαi−12∑i,jαiαjyiyjxi⊤xj\sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i,j} \alpha_i\alpha_j y_i y_j \boldsymbol{x}_i^\top \boldsymbol{x}_j∑i=1mαi−21∑i,jαiαjyiyjxi⊤xj ，本质是原问题 "最小化 12∥w∥2\frac{1}{2}\|\boldsymbol{w}\|^221∥w∥2 " 的对偶形式------ 通过拉格朗日对偶性，"原问题的极小" 等价于 "对偶问题的极大"。

对偶问题中的 "最大化目标函数"，自变量就是向量 α\boldsymbol{\alpha}α** === (α1,(\alpha_1,(α1, α2,...,\alpha_2, ...,α2,..., αm)\alpha_m)αm)** （每个样本对应一个 αi\alpha_iαi （拉格朗日乘子），核心是找到一组满足约束的 α\boldsymbol{\alpha}α，让对偶目标函数取得最大值

5-2、对偶问题与解的特性

一、拉格朗日乘子法：

第一步：引入拉格朗日乘子得到拉格朗日函数

引入拉格朗日乘子(αi≥0)( \alpha_i \geq 0 )(αi≥0)，构造拉格朗日函数： L(w,b,α)=12∣wL(\boldsymbol{w}, b, \boldsymbol{\alpha}) = \frac{1}{2} |\boldsymbol{w}L(w,b,α)=21∣w^2+∑i=12 + \sum_{i=1}2+∑i=1^mαi(1−yi(w⊤xi+b))]{m} \alpha_i \left( 1 - y_i(\boldsymbol{w}^\top \boldsymbol{x}_i + b) \right) ]mαi(1−yi(w⊤xi+b))]

第二步：令偏导为零的结果

对拉格朗日函数(L(w,b,α))( L(\boldsymbol{w}, b, \boldsymbol{\alpha}) )(L(w,b,α))关于 (w)( \boldsymbol{w} )(w)和 bbb 求偏导并令其为零，可得： w=∑i=1mαiyixi,0=∑i=1mαiyi\boldsymbol{w} = \sum_{i=1}^{m} \alpha_i y_i \boldsymbol{x}i, \quad 0 = \sum{i=1}^{m} \alpha_i y_iw=∑i=1mαiyixi,0=∑i=1mαiyi

第三步：回代得到对偶问题

将上述结果回代到拉格朗日函数中，得到对偶优化问题 ：max⁡α∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjxi⊤xj\max_{\boldsymbol{\alpha}} \quad \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j \boldsymbol{x}_i^\top \boldsymbol{x}jmaxα∑i=1mαi−21∑i=1m∑j=1mαiαjyiyjxi⊤xj s.t.∑i=1mαiyi=0,αi≥0,i=1,2,...,m\text{s.t.} \quad \sum{i=1}^{m} \alpha_i y_i = 0, \quad \alpha_i \geq 0, \quad i = 1,2,\dots,ms.t.∑i=1mαiyi=0,αi≥0,i=1,2,...,m 有闭式解！对偶问题可以通过SMO启发式算法，先找不符合KKT条件最大情况的样本点，再找举例改点最远的点。

二、对偶问题的核心求解步骤（3步走）

步骤1：选择合适的优化算法（解决"高维/多样本"求解效率问题）

对偶问题是凸二次规划（QP）问题 （目标函数是二次函数，约束是线性的），但直接用普通QP算法会因样本量 mmm 大而变慢（比如 m=104m=10^4m=104 时，计算量会爆炸）。因此SVM实际用的是专门优化稀疏QP的算法，核心是"只关注关键样本，避免全量计算"，最经典的是：

SMO算法（序列最小优化） ：把大问题拆成"最小的子问题"------每次只优化2个 αi\alpha_iαi 和 αj\alpha_jαj ，其他 α\alphaα 固定不变；
- 为什么能拆2个？因为约束 ∑i=1mαiyi=0\sum_{i=1}^m \alpha_i y_i = 0∑i=1mαiyi=0 是线性的，固定其他 α\alphaα 后，2个变量的关系可直接确定（比如 αj=−yj(∑k≠i,jαkyk)\alpha_j = -y_j (\sum_{k≠i,j} \alpha_k y_k)αj=−yj(∑k=i,jαkyk) ），子问题能直接解析求解，不用迭代；
- 优势：速度快、内存占用小，适合大样本/高维数据，是SVM的标准求解算法。

其他可选算法：

内点法：适合小样本、低维数据，求解精度高但速度慢；
梯度上升法：简单易实现，但需要调学习率，精度不如SMO。

步骤2：用SMO算法迭代求解 α\boldsymbol{\alpha}α （核心操作）

SMO的核心逻辑是"循环迭代，逐步优化"，具体流程：

初始化 ：所有 αi=0\alpha_i = 0αi=0 （满足约束 ∑αiyi=0\sum \alpha_i y_i = 0∑αiyi=0 ）；
**选择待优化的一对 ** (αi,αj)(\alpha_i, \alpha_j)(αi,αj) ：
- 选"违反KKT条件最严重"的样本（比如 αi>0\alpha_i > 0αi>0 但 yif(xi)<1y_i f(x_i) < 1yif(xi)<1 ，说明样本没满足边界约束，需要调整）；
- 再选一个辅助样本 jjj （通常选能让目标函数下降最多的）；
解析求解子问题：
- 利用约束 αiyi+αjyj=C\alpha_i y_i + \alpha_j y_j = Cαiyi+αjyj=C （ CCC 是常数，由其他固定的 α\alphaα 决定），把目标函数转化为单变量函数（只含 αi\alpha_iαi 或 αj\alpha_jαj ）；
- 求这个单变量函数的最大值，得到 αi\alpha_iαi 和 αj\alpha_jαj 的新值；
裁剪新值 ：保证 αi,αj≥0\alpha_i, \alpha_j \geq 0αi,αj≥0 （满足约束）；
重复迭代 ：直到所有样本都满足KKT条件（或迭代次数达到上限），此时的 α\boldsymbol{\alpha}α 就是最优解。

步骤3：由最优 α\boldsymbol{\alpha}α 反推模型参数 w\boldsymbol{w}w 和 bbb

求解出最优 α∗=(α1∗,α2∗,...,αm∗)\boldsymbol{\alpha}^* = (\alpha_1^*, \alpha_2^*, ..., \alpha_m^*)α∗=(α1∗,α2∗,...,αm∗) 后，直接用之前的偏导结果反推：

求 w∗\boldsymbol{w}^*w∗ ：由 w=∑i=1mαiyixi\boldsymbol{w} = \sum_{i=1}^m \alpha_i y_i \boldsymbol{x}iw=∑i=1mαiyixi ，代入最优 αi∗\alpha_i^*αi∗ ： w∗=∑i:αi∗>0αi∗yixi\boldsymbol{w}^* = \sum{i: \alpha_i^* > 0} \alpha_i^* y_i \boldsymbol{x}_iw∗=∑i:αi∗>0αi∗yixi （只有 αi∗>0\alpha_i^* > 0αi∗>0 的样本（支持向量）才贡献，其他 αi∗=0\alpha_i^* = 0αi∗=0 可忽略，体现稀疏性）；
求 b∗b^*b∗ ：利用KKT条件中的 αi∗(1−yif(xi))=0\alpha_i^* (1 - y_i f(x_i)) = 0αi∗(1−yif(xi))=0 ------对任意一个支持向量（ αi∗>0\alpha_i^* > 0αi∗>0 ），必有 1−yif(xi)=01 - y_i f(x_i) = 01−yif(xi)=0 ，即 f(xi)=yif(x_i) = y_if(xi)=yi ；而 f(xi)=w∗⊤xi+b∗=yif(x_i) = \boldsymbol{w}^{*\top} x_i + b^* = y_if(xi)=w∗⊤xi+b∗=yi ，整理得： b∗=yi−w∗⊤xib^* = y_i - \boldsymbol{w}^{*\top} x_ib∗=yi−w∗⊤xi （实际中会用所有支持向量计算 b∗b^*b∗ 取平均值，提高稳定性）。

三、解的特性：

最终模型：

将对偶问题得到的w=∑i=1mαiyixi\boldsymbol{w} = \sum_{i=1}^{m} \alpha_i y_i \boldsymbol{x}iw=∑i=1mαiyixi代入分类函数，最终模型为：f(x)=w⊤x+b=∑i=1mαiyixi⊤x+bf(\boldsymbol{x}) = \boldsymbol{w}^\top \boldsymbol{x} + b = {\sum{i=1}^{m} \alpha_i y_i \boldsymbol{x}_i^\top \boldsymbol{x}} + bf(x)=w⊤x+b=∑i=1mαiyixi⊤x+b

KKT 条件：

SVM 优化问题满足的 KKT 条件（最优解的必要条件）：{αi≥0 ;1−yif(xi)≤0 ;αi(1−yif(xi))=0 .\begin{cases} \alpha_i \geq 0 \, ; \\ 1 - y_i f(\boldsymbol{x}_i) \leq 0 \, ; \\ \alpha_i \left( 1 - y_i f(\boldsymbol{x}_i) \right) = 0 \, . \end{cases}⎩ ⎨ ⎧αi≥0;1−yif(xi)≤0;αi(1−yif(xi))=0.

由第三个条件可推出：必有 αi\alpha_iαi** === 000** 或 yif(xi)y_i f(\boldsymbol{x}_i)yif(xi) === 111 。

解的稀疏性：训练完成后，最终模型仅与 αi≠0\alpha_i \neq 0αi=0 对应的样本（即支持向量）有关。支持向量机（Support Vector Machine, SVM）也因此得名。

SVM 之所以 "只和支持向量有关"，本质是 对偶优化和 KKT 条件共同作用下的稀疏性结果：

对偶问题的优化目标，最终会让大部分样本的 αi∗=0\alpha_i^* = 0αi∗=0（非支持向量），仅保留关键的边界样本；
模型参数 w∗,b∗\boldsymbol{w}^*, b^*w∗,b∗ 和预测函数，都只依赖 αi∗>0\alpha_i^* > 0αi∗>0 的样本，非支持向量的信息被完全屏蔽；
这一特性不仅让 SVM 计算高效（预测时无需遍历所有样本），更保证了泛化能力 ------ 支持向量是最能反映数据分布的 "关键样本"，用它们定义的超平面更稳健。

SVM 的核心是找到「两类样本间间隔最大的超平面」，这个超平面的位置和方向，仅由「两类样本的边界样本」（支持向量）决定：

非支持向量：要么在间隔内部（离超平面较远），要么在间隔外部，它们的存在与否，不会改变 "最大间隔" 的位置 ------ 就像用尺子量长度时，只有两端的标记点（支持向量）决定了长度，中间的点不影响结果；
支持向量：恰好落在间隔边界上 yif(xi)=1y_i f(\boldsymbol{x}_i) = 1yif(xi)=1，是两类样本的 "临界样本"，它们的位置直接决定了超平面能 "推到多远"（即间隔多大）

5-3、特征空间映射

核心问题：若不存在一个能正确划分两类样本的超平面，怎么办？

解决思路：将样本从原始空间映射到一个更高维的特征空间，使样本在这个特征空间内线性可分。

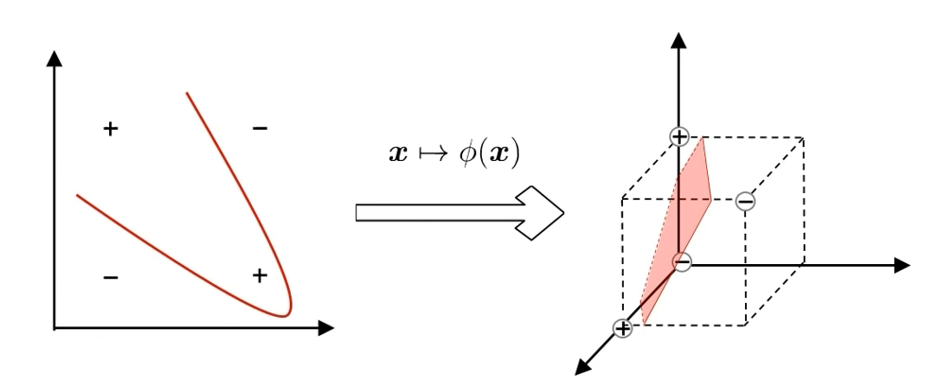
图示说明：

左侧：原始空间中，两类样本（+、-）无法用直线（超平面）划分。
中间：通过映射 x↦ϕ(x)\boldsymbol{x} \mapsto \phi(\boldsymbol{x})x↦ϕ(x)转换样本。
右侧：高维特征空间中，两类样本可被超平面（图中粉色平面）线性划分。

结论：如果原始空间是有限维（属性数有限），那么一定存在一个高维特征空间使样本线性可分

设定：设样本 x\boldsymbol{x}x 映射后的向量为 ϕ(x)\phi(\boldsymbol{x})ϕ(x) ，划分超平面为 f(x)=w⊤ϕ(x)+bf(\boldsymbol{x}) = \boldsymbol{w}^\top \phi(\boldsymbol{x}) + bf(x)=w⊤ϕ(x)+b

在特征空间中：

原始问题：

目标：最小化 12∣w∣2\frac{1}{2}|\boldsymbol{w}|^221∣w∣2

约束： yi(w⊤ϕ(xi)+b)≥1, i=1,2,...,my_i(\boldsymbol{w}^\top \phi(\boldsymbol{x}_i) + b) \geq 1, \ i=1,2,\dots,myi(w⊤ϕ(xi)+b)≥1, i=1,2,...,m

对偶问题

目标：最大化 ∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjϕ(xi)⊤ϕ(xj)\sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \boxed{ \phi(\boldsymbol{x}_i)^\top \phi(\boldsymbol{x}_j)}∑i=1mαi−21∑i=1m∑j=1mαiαjyiyjϕ(xi)⊤ϕ(xj)

约束： ∑i=1mαiyi=0\sum_{i=1}^m \alpha_i y_i = 0∑i=1mαiyi=0 ， αi≥0, i=1,2,...,m\alpha_i \geq 0, \ i=1,2,\dots,mαi≥0, i=1,2,...,m

预测

f(x)=w⊤ϕ(x)+b=∑i=1mαiyiϕ(xi)⊤ϕ(x)+bf(\boldsymbol{x}) = \boldsymbol{w}^\top \phi(\boldsymbol{x}) + b = \sum_{i=1}^m \alpha_i y_i \boxed{\phi(\boldsymbol{x}_i)^\top \phi(\boldsymbol{x})} + bf(x)=w⊤ϕ(x)+b=∑i=1mαiyiϕ(xi)⊤ϕ(x)+b

关键提示：高维向量计算复杂，可以只需要直接计算内积（因为映射后的向量仅以内积形式出现）。‍

5-4、核函数(Kernel Function)

基本思路：设计核函数

k(xi,xj)=ϕ(xi)Tϕ(xj) k(\boldsymbol{x}_i, \boldsymbol{x}_j) = \phi(\boldsymbol{x}_i)^\text{T}\phi(\boldsymbol{x}_j) k(xi,xj)=ϕ(xi)Tϕ(xj)

绕过显式考虑特征映射、以及计算高维内积的困难

Mercer定理 ：若一个对称函数所对应的核矩阵半正定，则它就能作为核函数来使用

任何一个核函数，都隐式地定义了一个RKHS (Reproducing Kernel Hilbert Space, 再生核希尔伯特空间)

"核函数选择"成为决定支持向量机性能的关键！

核函数作为高维空间距离计算矩阵,

核函数选择从核函数集合保证模型最优，不可能最优，要求尽可能好

再生希尔伯特空间与核函数的关联

再生希尔伯特空间（Reproducing Kernel Hilbert Space，简称RKHS）是一种特殊的希尔伯特空间，核心特点是存在"再生核" ，能通过核函数直接计算空间中函数的内积，避免显式处理高维空间。

核心定义

再生希尔伯特空间是定义在集合 X\mathcal{X}X 上的函数空间 H\mathcal{H}H （同时是希尔伯特空间），满足：

存在一个再生核 κ:X×X→R\kappa: \mathcal{X} \times \mathcal{X} \to \mathbb{R}κ:X×X→R ，使得：

对任意 x∈Xx \in \mathcal{X}x∈X ， κ(⋅,x)∈H\kappa(\cdot, x) \in \mathcal{H}κ(⋅,x)∈H （核函数本身是空间中的函数）；
再生性 ：对任意 f∈Hf \in \mathcal{H}f∈H 和 x∈Xx \in \mathcal{X}x∈X ，有 f(x)=⟨f,κ(⋅,x)⟩Hf(x) = \langle f, \kappa(\cdot, x) \rangle_{\mathcal{H}}f(x)=⟨f,κ(⋅,x)⟩H （函数在 xxx 处的取值，等于它与核函数 κ(⋅,x)\kappa(\cdot, x)κ(⋅,x) 在空间中的内积）。

与核函数的关系

任何一个核函数 κ(xi,xj)\kappa(x_i, x_j)κ(xi,xj) ，都隐式地定义了一个唯一的再生希尔伯特空间（即该核对应的RKHS）。

这也是SVM中使用核函数的关键：通过核函数，我们可以直接在RKHS中计算函数内积，无需显式构造高维特征空间。

作用（以SVM为例）

在SVM的对偶问题中，高维特征空间的内积 ϕ(xi)⊤ϕ(xj)\phi(x_i)^\top \phi(x_j)ϕ(xi)⊤ϕ(xj) 可以用核函数 κ(xi,xj)\kappa(x_i, x_j)κ(xi,xj) 代替，而这个核函数对应的正是RKHS中的内积------既绕开了高维计算，又保证了数学严谨性。

5-5、SVM简史

核心时间线：

1963 年：Vapnik 提出支持向量的概念
1968 年：Vapnik 和 Chervonenkis 提出 VC 维
1974 年：提出结构风险最小化原则
...... 苏联解体前一年（1990）：Vapnik 来到美国
1995 年：《Support Vector Network》文章发表；《The Nature of Statistical Learning》出版
1998 年：SVM 在文本分类上取得巨大成功；《Statistical Learning Theory》出版
......

"Nothing is more practical than a good theory" -- V. Vapnik

"没有什么比一个好的理论更加具有 practical"

‍