WPF 力导引算法实现图布局

WPF 力导引算法实现图布局

1 经典基础算法

1. Eades 算法 (1984)

   • 核心思想：最早引入"弹簧-质点"模型的算法，边模拟为弹簧（吸引力），非邻接节点间模拟为斥力。

   • 特点：简单直观，但收敛较慢，易陷入局部最优。

2. Fruchterman-Reingold 算法 (1991)

   • 核心思想：引入"温度"概念控制位移幅度，迭代中温度逐渐降低（类似模拟退火）。

   • 力模型：

     • 吸引力：与边长度成正比（f_a = d^2 / k，d为边长，k为理想边长）。

     • 斥力：与节点距离平方成反比（f_r = -k^2 / d）。

   • 特点：布局紧凑均匀，适用于中小规模网络。

3. Kamada-Kawai 算法 (1989)

   • 核心思想 ：基于能量最小化，目标是将所有节点对的几何距离逼近其图论最短路径长度。

   • 特点：能较好展现全局结构，但计算所有节点对最短路径开销大，适用于数百节点的图。

2 高性能优化算法（适合大规模网络）

4. Barnes-Hut 近似算法 (基于四叉树/八叉树)

   • 核心思想：将远距离节点群近似为单个质心，将斥力计算复杂度从 O(N²) 降为 O(N log N)。

   • 应用：常用于天体物理的N-body问题，被集成到许多力导引布局工具中。

5. ForceAtlas2 (2011)

   • 核心思想：专为Gephi软件设计的算法，在FR基础上改进：

     • 引入度依赖的斥力（高度数节点产生更强斥力，避免中心重叠）。

     • 支持边缘权重调整吸引力。

     • 采用自适应温度 和防止震荡的阻尼。

   • 特点：适合复杂真实网络（如社交网络），布局层次清晰。

6. LinLog 模型

   • 核心思想 ：优化能量函数为U = Σ边的距离 - Σ节点对的log(距离)，强调聚类结构。

   • 特点：同一簇内节点更紧密，簇间距离更明显。

3 代码实现

1. 数据模型

/// <summary>
/// 节点
/// </summary>
public class Node
{
    public string Id { get; set; }
    public double X { get; set; }
    public double Y { get; set; }
    public double Radius { get; set; }
    // 布局计算中使用的临时变量
    internal double DX { get; set; } // X轴位移/速度
    internal double DY { get; set; } // Y轴位移/速度
    internal int Degree { get; set; } // 节点的度（连接数）

    public Node(string id, double radius = 5.0)
    {
        Id = id;
        Radius = radius;
    }

    public override string ToString() => $"Node[{Id}]: ({X:F2}, {Y:F2})";
}

/// <summary>
/// 关系
/// </summary>
public class Relationship
{
    public string Id { get; set; }
    public string SourceId { get; set; }
    public string TargetId { get; set; }

    public Relationship(string source, string target)
    {
        SourceId = source;
        TargetId = target;
        Id = Guid.NewGuid().ToString();
    }

    public Relationship(string source, string target, string id)
    {
        SourceId = source;
        TargetId = target;
        Id = id;
    }
}

/// <summary>
/// 图结构
/// </summary>
public class Graph
{
    public Dictionary<string, Node> Nodes { get; set; }
    public Dictionary<string, Relationship> Relationships { get; set; }

    public Graph()
    {
        Nodes = new Dictionary<string, Node>();
        Relationships = new Dictionary<string, Relationship>();
    }

    public void AddNode(Node node)
    {
        Nodes[node.Id] = node;
    }

    public void AddRelationship(Relationship relationship)
    {
        Relationships[relationship.Id] = relationship;
    }
}

/// <summary>
/// 矩形布局范围
/// </summary>
public struct LayoutBounds
{
    public double MinX;
    public double MaxX;
    public double MinY;
    public double MaxY;

    public LayoutBounds(double x, double y, double width, double height)
    {
        MinX = x;
        MinY = y;
        MaxX = x + width;
        MaxY = y + height;
    }

    public double Width => MaxX - MinX;
    public double Height => MaxY - MinY;

    public double CenterX => (MinX + MaxX) / 2.0;
    public double CenterY => (MinY + MaxY) / 2.0;
}

2. 核心算法

public class LinLogLayout
{
    // 配置参数
    private const int Iterations = 100;             // 迭代次数
    private const double RepulsionForce = 20.0;     // 斥力
    private const double AttractionForce = 1.0;     // 引力
    private const double StepSize = 0.8;            // 稍微调大初始步长以适应约束
    private const double Decay = 0.97;              // 衰变系数
    private const double GravityStrength = 0.01;    // 强度越大，图越紧凑在中央
    private const double MinClearance = 0.1;        // 斥力计算的最小安全距离（防止除以零，并作为最小非重叠缓冲）
    private const double Epsilon = 1e-6;            // 防止除以零的微小值 (Epsilon)
    private const double MaxMovementPerStep = 2.0;  // 限制节点单步最大移动距离。值越小，越稳定，但收敛越慢。在边界小的情况下，此值应适当减小。

    /// <summary>
    /// 执行布局计算
    /// </summary>
    /// <param name="nodes">节点列表</param>
    /// <param name="relations">关系列表</param>
    /// <param name="bounds">矩形限制范围</param>
    public void ComputeLayout(List<Node> nodes, List<Relationship> relations, LayoutBounds bounds)
    {
        if (nodes == null || nodes.Count == 0) return;

        // 1. 初始化：将节点随机放置在边界范围内
        //    这比在(0,0)附近随机更好，避免一开始就飞出很远
        Random rnd = new Random();
        foreach (var n in nodes)
        {
            // 如果节点还没坐标（或是0,0），给一个范围内的随机值
            if (Math.Abs(n.X) < 0.001 && Math.Abs(n.Y) < 0.001)
            {
                n.X = bounds.MinX + rnd.NextDouble() * bounds.Width;
                n.Y = bounds.MinY + rnd.NextDouble() * bounds.Height;
            }
        }

        var nodeDict = nodes.ToDictionary(n => n.Id);

        // 筛选有效关系
        var validRelations = relations
            .Where(r => nodeDict.ContainsKey(r.SourceId) && nodeDict.ContainsKey(r.TargetId))
            .ToList();

        double currentStep = StepSize;

        // 2. 迭代循环
        for (int i = 0; i < Iterations; i++)
        {
            // 重置力向量
            foreach (var n in nodes) { n.DX = 0; n.DY = 0; }

            // --- A. 计算斥力 (Repulsion) 考虑 Radius ---
            for (int a = 0; a < nodes.Count; a++)
            {
                var nodeA = nodes[a];
                for (int b = a + 1; b < nodes.Count; b++)
                {
                    var nodeB = nodes[b];

                    double dx = nodeA.X - nodeB.X;
                    double dy = nodeA.Y - nodeB.Y;
                    double distSq = dx * dx + dy * dy;
                    double dist = Math.Sqrt(distSq); // 节点中心点的实际距离
                    // NaN 保护机制 1: 检查中心距离是否为零
                    if (dist < Epsilon)
                    {
                        // 节点完全重叠，施加随机扰动以获得方向
                        dx = rnd.NextDouble() * 2 * Epsilon;
                        dy = rnd.NextDouble() * 2 * Epsilon;
                        dist = Math.Sqrt(dx * dx + dy * dy);
                        // 确保 dist 不会是 NaN 或零
                        if (dist < Epsilon) dist = Epsilon;
                    }
                    // 1. 计算两个节点半径之和
                    double sumOfRadii = nodeA.Radius + nodeB.Radius;

                    // 2. 计算节点表面之间的净空距离 (Clearance)
                    double clearance = dist - sumOfRadii;

                    // 3. 确定用于斥力计算的有效距离 (Effective Distance)
                    // 如果节点重叠 (clearance <= 0)，将有效距离强制设为 MinClearance (0.1) 
                    // 这将产生巨大的斥力来推开重叠的节点
                    double effectiveDist = Math.Max(clearance, MinClearance);

                    // 4. 应用 LinLog 斥力公式: F = K / effectiveDist
                    // 注意：这里的斥力是基于表面距离的，而不是中心距离。
                    double force = RepulsionForce / effectiveDist;

                    // 5. 应用斥力 (方向仍基于中心点连线)
                    double fx = (dx / dist) * force;
                    double fy = (dy / dist) * force;

                    nodeA.DX += fx; nodeA.DY += fy;
                    nodeB.DX -= fx; nodeB.DY -= fy;
                }
            }

            // --- B. 计算引力 (Attraction) ---
            foreach (var rel in validRelations)
            {
                var u = nodeDict[rel.SourceId];
                var v = nodeDict[rel.TargetId];

                double dx = v.X - u.X;
                double dy = v.Y - u.Y;
                double distSq = dx * dx + dy * dy;
                double dist = Math.Sqrt(distSq);
                // NaN 保护机制 2: 检查中心距离是否为零
                if (dist < Epsilon)
                {
                    // 节点重叠，跳过引力计算（让斥力将它们推开）
                    continue;
                }

                // LinLog Attraction
                double force = AttractionForce;

                double fx = (dx / dist) * force;
                double fy = (dy / dist) * force;

                u.DX += fx;
                u.DY += fy;
                v.DX -= fx;
                v.DY -= fy;
            }

            // --- C. 计算中心引力 (Central Gravity) ---
            double centerX = bounds.CenterX;
            double centerY = bounds.CenterY;

            foreach (var n in nodes)
            {
                double dx = n.X - centerX; // 节点指向中心的向量是 -dx
                double dy = n.Y - centerY;
                double dist = Math.Sqrt(dx * dx + dy * dy);

                // NaN 保护机制 3: 检查距离是否为零
                if (dist < Epsilon)
                {
                    // 节点在中心点，力为零，跳过计算
                    continue;
                }

                double force = GravityStrength * dist;

                n.DX -= (dx / dist) * force;
                n.DY -= (dy / dist) * force;
            }

            // --- D. 更新位置并应用边界约束 ---
            foreach (var n in nodes)
            {
                // 1. 计算理论位移
                double movementX = n.DX * currentStep;
                double movementY = n.DY * currentStep;

                double movementDist = Math.Sqrt(movementX * movementX + movementY * movementY);

                // 2. 限制最大位移
                if (movementDist > MaxMovementPerStep)
                {
                    // 如果超出最大限制，按比例缩小位移向量
                    double ratio = MaxMovementPerStep / movementDist;
                    movementX *= ratio;
                    movementY *= ratio;
                }

                // 3. 应用位移
                n.X += movementX;
                n.Y += movementY;

                // 4. 矩形边界硬约束
                if (n.X < bounds.MinX) n.X = bounds.MinX;
                else if (n.X > bounds.MaxX) n.X = bounds.MaxX;

                if (n.Y < bounds.MinY) n.Y = bounds.MinY;
                else if (n.Y > bounds.MaxY) n.Y = bounds.MaxY;
            }
            //foreach (var n in nodes)
            //{
            //    // 移动
            //    n.X += n.DX * currentStep;
            //    n.Y += n.DY * currentStep;

            //    // 边界限制 (Clamping)
            //    if (n.X < bounds.MinX) n.X = bounds.MinX;
            //    else if (n.X > bounds.MaxX) n.X = bounds.MaxX;

            //    if (n.Y < bounds.MinY) n.Y = bounds.MinY;
            //    else if (n.Y > bounds.MaxY) n.Y = bounds.MaxY;
            //}

            // --- E. 冷却 ---
            currentStep *= Decay;
        }
    }
}

效果Demo：

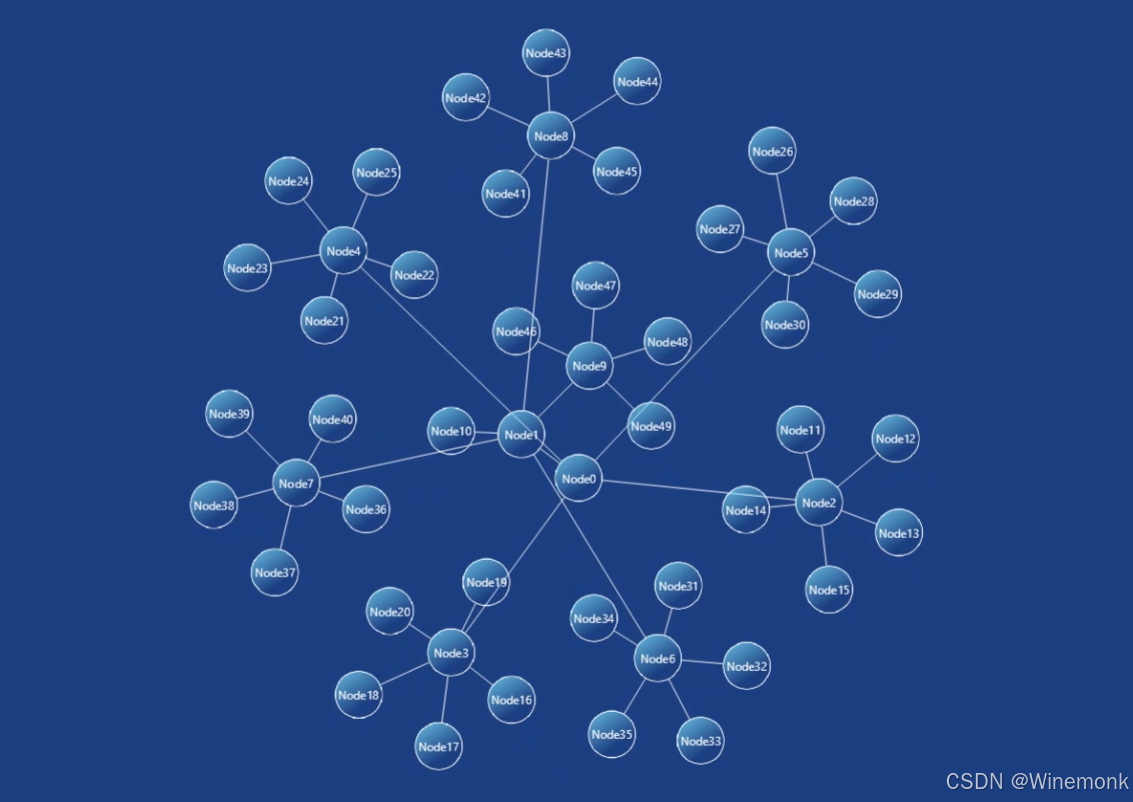
效果视频：

https://live.csdn.net/v/504775
https://raw.githubusercontent.com/Winemonk/images/master/blog/post/202512091617226.mp4