第六章 二叉树 part02
226.翻转二叉树 (优先掌握递归)
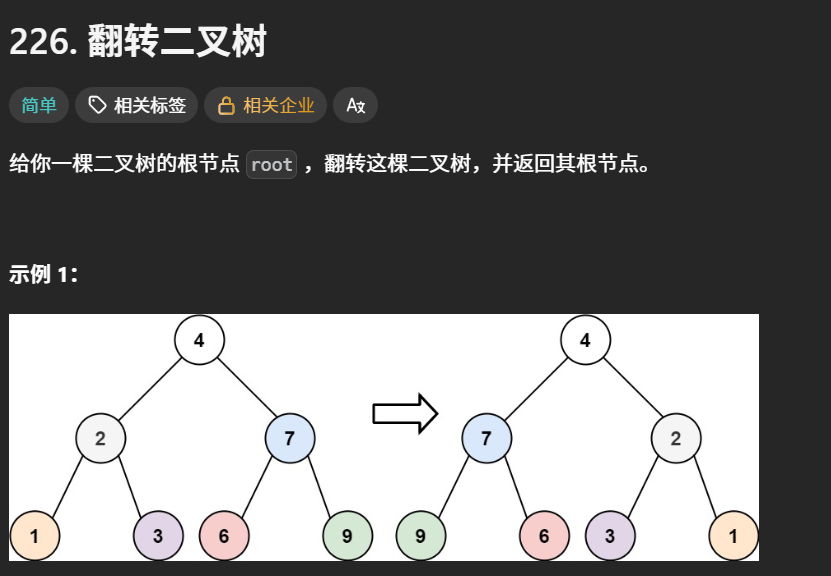
也是先选择的简单的迭代方法,将节点存在栈中,从栈中提取要处理的节点,进行左右子树的交换,然后再将其左右子树放入栈中。
python
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root is None:
return None
stack = [root]
while stack:
node = stack.pop()
node.left , node.right = node.right ,node.left
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return root下面是递归的方法,但是why呢?
递归这里还是很晕啊,理解是分解问题,反转二叉树相当于反转子树,然后交换左右子树,顺序倒过来也可以,结束条件是到达空节点。这里的root类似一个cur
python
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root is None:
return None
node = root
node.right ,node.left = node.left , node.right
self.invertTree(root.left)
self.invertTree(root.right)
return root101. 对称二叉树 (优先掌握递归)
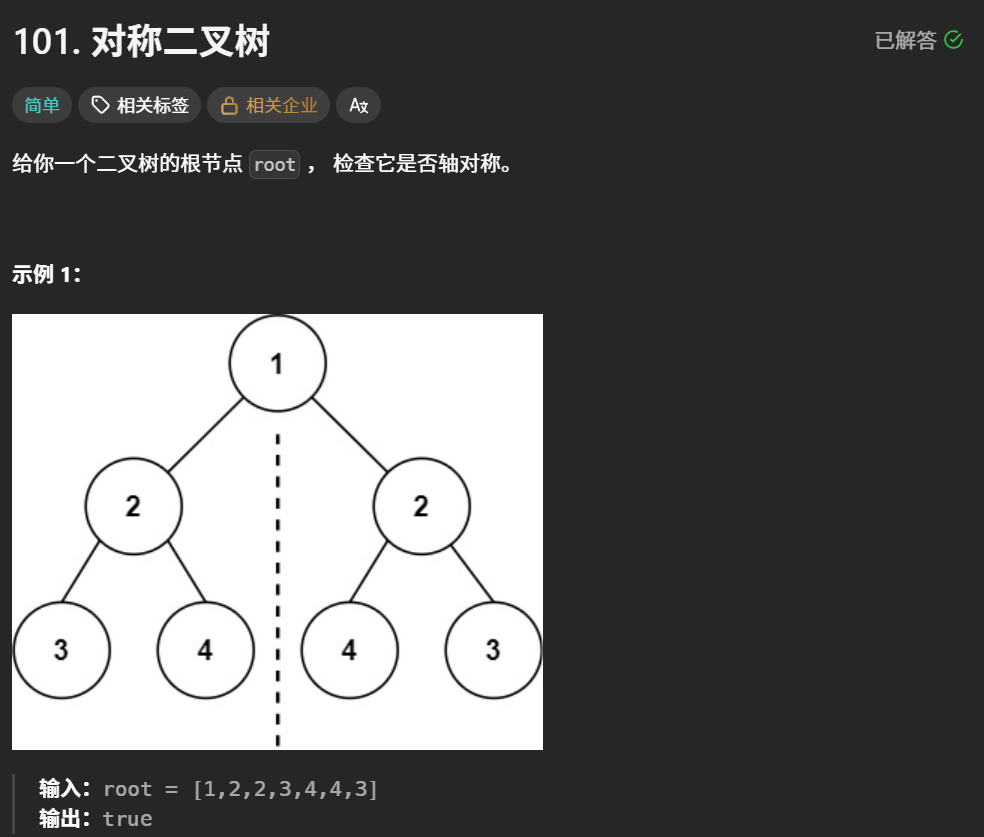
递归法
递归三部曲
确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。返回值自然是bool类型。
代码如下:
php
cp(self, left, right)确定终止条件
要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
节点为空的情况有:(注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点)
- 左节点为空,右节点不为空,不对称,return false
- 左不为空,右为空,不对称 return false
- 左右都为空,对称,返回true
此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
- 左右都不为空,比较节点数值,不相同就return false
此时左右节点不为空,且数值也不相同的情况我们也处理了。
代码如下:
php
if not left and not right:
return True
elif not left and right:
return False
elif left and not right:
return False
elif left.val != right.val:
return False
else:我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
确定单层递归的逻辑
此时才进入单层递归的逻辑,单层递归的逻辑就是处理 左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内侧是否对称,传入左节点的右孩子,右节点的左孩子。
- 如果左右都对称就返回true ,有一侧不对称就返回false 。
代码如下:
python
outside = self.cp(left.left, right.right)
inside = self.cp(left.right, right.left)
return (outside and inside)
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
return self.cp(root.left, root.right)
def cp(self, left, right):
if not left and not right:
return True
elif not left and right:
return False
elif left and not right:
return False
elif left.val != right.val:
return False
else:
outside = self.cp(left.left, right.right)
inside = self.cp(left.right, right.left)
return (outside and inside)104.二叉树的最大深度 (优先掌握递归)
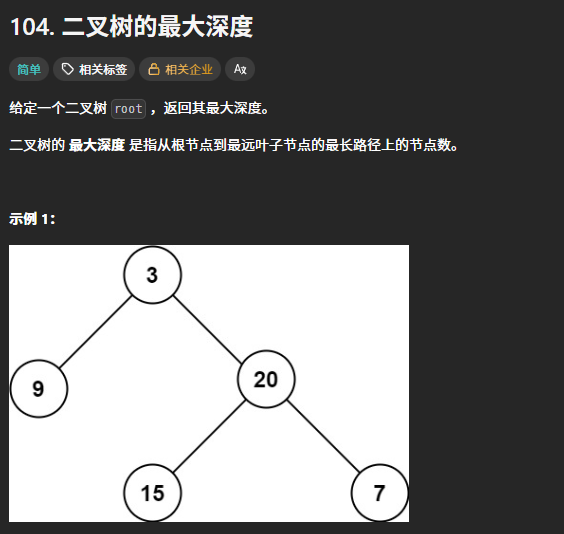
这里把大问题分解为小问题,计算整棵树的最大深度相当于计算左右子树的最大深度。当当前节点为空时,返回0即可。
python
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right))+1好懂一点的思路,就是不管递归具体每一步怎么做,直接考虑假设任务完成,那么左右子树都到头了时候,返回深度即可
python
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
left_depth = self.maxDepth(root.left)
right_depth = self.maxDepth(root.right)
return max(left_depth ,right_depth)+1111.二叉树的最小深度 (优先掌握递归)
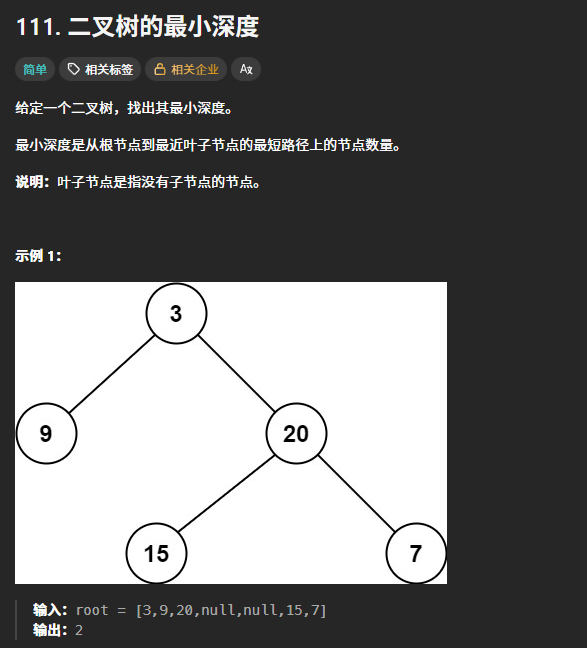
该题和上面不一样的点就是对于最后取值判断,当有一边没有叶子节点时,需要去取另一侧的最小值
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
while root is None:
return 0
minleft = self.minDepth(root.left)
minright = self.minDepth(root.right)
if root.left is None and root.right is not None:
return minright+1
if root.left is not None and root.right is None:
return minleft+1
return min(minleft, minright) + 1递归好难懂。也可能是题目理解上有问题,导致递归写不好。
康复训练的康复训练,堂堂复活了