注:博主并非旨在对针对文章中提及论文的实验设计、数据及结果进行逐一还原,而是针对其核心方法论或关键创新点,通过自行设计的实验流程进行验证与探索。若是完整的论文复现,会进行提前说明。
1 论文简介
《A Robust Fuzzy Local Information C-Means Clustering Algorithm》是由 Stelios Krinidis 和 Vassilios Chatzis 于 2010 年 5 月发表在 《IEEE Transactions on Image Processing》 上的一篇论文。该论文针对传统模糊 C 均值算法及其改进版本在图像分割中对噪声敏感、过度依赖需要人工调整的关键参数(如 aaa, λ\lambdaλ)等问题,提出了一种全新的鲁棒模糊局部信息 C 均值聚类算法。该方法的核心创新在于定义了一个模糊因子 GkiG_{ki}Gki,该因子能够以模糊的方式,自适应地融合每个像素的局部空间邻域信息和局部灰度级信息,而无需引入任何需要经验设定的平衡参数。FLICM 直接在原始图像上进行迭代聚类,既避免了预处理可能导致的细节丢失,又实现了对噪声和异常值的鲁棒性,同时较好地保持了图像细节。因其完全无需参数选择且对高斯噪声、均匀噪声、椒盐噪声等多种噪声类型均表现出良好鲁棒性的特点,该方法被广泛应用于噪声图像分割领域,为后续许多结合局部信息的模糊聚类研究提供了重要的思路和框架,在图像处理与计算机视觉领域具有一定的影响力。
论文的目标函数并非严格上最小化 FLICM 目标函数,从 3 实验结果 可以看出目标函数值先下降后上升,根据 Szilágyi 论文《Lessons to learn from a mistaken optimization》,其主要原因为 FLICM 的迭代公式不是从目标函数通过拉格朗日乘子法正确推导出来的,虽然最后仍能收敛到看似合理的聚类中心,是因为 FLICM 实际上是一种启发式算法,而不是真正的优化算法。
2 算法原理
假设有待分割的图像,其像素集合为 X={x1,x2,...,xN}\mathbf{X} = \{x_1, x_2, \ldots, x_N\}X={x1,x2,...,xN},目标聚类数为 ccc,模糊加权指数为 mmm。
步骤 1:引入模糊局部因子 GkiG_{ki}Gki
FLICM 算法的核心是定义了一个模糊因子 GkiG_{ki}Gki,用于度量像素 iii 对于第 kkk 个簇的局部(空间和灰度)约束。其公式定义为:
Gki=∑j∈Nij≠i1dij+1(1−ukj)m∥xj−vk∥2G_{ki} = \sum_{\substack{j \in N_i \\ j \neq i}} \frac{1}{d_{ij}+1}(1 - u_{kj})^{m} \| x_j - v_k \|^2Gki=j∈Nij=i∑dij+11(1−ukj)m∥xj−vk∥2
其中,NiN_iNi 是以像素 iii 为中心的局部窗口(如 3×33 \times 33×3)内的邻居像素集合;dijd_{ij}dij 是像素 iii 和 jjj 之间的空间欧氏距离;ukju_{kj}ukj 是邻居像素 jjj 属于第 kkk 个簇的模糊隶属度;vkv_kvk 是第 kkk 个簇的中心(原型)。该因子巧妙地将空间距离(1/(dij+1)1/(d_{ij}+1)1/(dij+1))、邻居像素的隶属度不确定性((1−ukj)m(1 - u_{kj})^{m}(1−ukj)m)以及邻居像素与簇中心的灰度差异(∥xj−vk∥2\| x_j - v_k \|^2∥xj−vk∥2)融合在一起,无需任何人工参数来平衡各项。
步骤 2:构建 FLICM 目标函数
将模糊因子 GkiG_{ki}Gki 融入传统的 FCM 目标函数中,得到 FLICM 的目标函数 JmJ_mJm:
Jm=∑i=1N∑k=1c[ukim∥xi−vk∥2+Gki]J_m = \sum_{i=1}^{N} \sum_{k=1}^{c} \left[ u_{ki}^m \| x_i - v_k \|^2 + G_{ki} \right]Jm=i=1∑Nk=1∑c[ukim∥xi−vk∥2+Gki]
该函数旨在最小化每个像素到其所属簇中心的灰度距离,同时受到其局部邻域像素信息的模糊约束。
步骤 3:推导迭代更新公式
通过拉格朗日乘子法最小化目标函数 JmJ_mJm,可得到隶属度 ukiu_{ki}uki 和簇中心 vkv_kvk 的迭代更新公式。隶属度 ukiu_{ki}uki 更新公式为:
uki=1∑j=1c(∥xi−vk∥2+Gki∥xi−vj∥2+Gji)1/(m−1)u_{ki} = \frac{1}{\sum_{j=1}^{c} \left( \frac{\| x_i - v_k \|^2 + G_{ki}}{\| x_i - v_j \|^2 + G_{ji}} \right)^{1/(m-1)}}uki=∑j=1c(∥xi−vj∥2+Gji∥xi−vk∥2+Gki)1/(m−1)1
簇中心 vkv_kvk 更新公式为:
vk=∑i=1Nukimxi∑i=1Nukimv_k = \frac{\sum_{i=1}^{N} u_{ki}^m x_i}{\sum_{i=1}^{N} u_{ki}^m}vk=∑i=1Nukim∑i=1Nukimxi
值得注意的是,簇中心的更新公式与传统 FCM 一致,因为 GkiG_{ki}Gki 中不包含 xix_ixi,对 vkv_kvk 求导时该项为零。
步骤 4:执行迭代聚类流程
- 设定聚类数 ccc、模糊指数 mmm 和停止阈值 ϵ\epsilonϵ。
- 随机初始化模糊隶属度矩阵 U(0)U^{(0)}U(0)。
- 根据公式 vk=∑i=1Nukimxi∑i=1Nukimv_k = \frac{\sum_{i=1}^{N} u_{ki}^m x_i}{\sum_{i=1}^{N} u_{ki}^m}vk=∑i=1Nukim∑i=1Nukimxi 计算当前簇中心。
- 根据公式 uki=1∑j=1c(∥xi−vk∥2+Gki∥xi−vj∥2+Gji)1/(m−1)u_{ki} = \frac{1}{\sum_{j=1}^{c} \left( \frac{\| x_i - v_k \|^2 + G_{ki}}{\| x_i - v_j \|^2 + G_{ji}} \right)^{1/(m-1)}}uki=∑j=1c(∥xi−vj∥2+Gji∥xi−vk∥2+Gki)1/(m−1)1
- 更新隶属度矩阵。
- 检查隶属度矩阵变化是否小于 ϵ\epsilonϵ,若是则停止迭代,否则返回步骤 3。
步骤 5:去模糊化得到最终分割结果
迭代收敛后,对最终的模糊隶属度矩阵进行去模糊化,通常采用最大隶属度法则:将每个像素 iii 分配给隶属度最高的那个簇,即 Ci=argmaxk{uki},k=1,2,...,cC_i = \arg\max_k \{ u_{ki} \}, \quad k = 1, 2, \ldots, cCi=argmaxk{uki},k=1,2,...,c,从而得到清晰的二值或多值分割图像。
3 实验结果
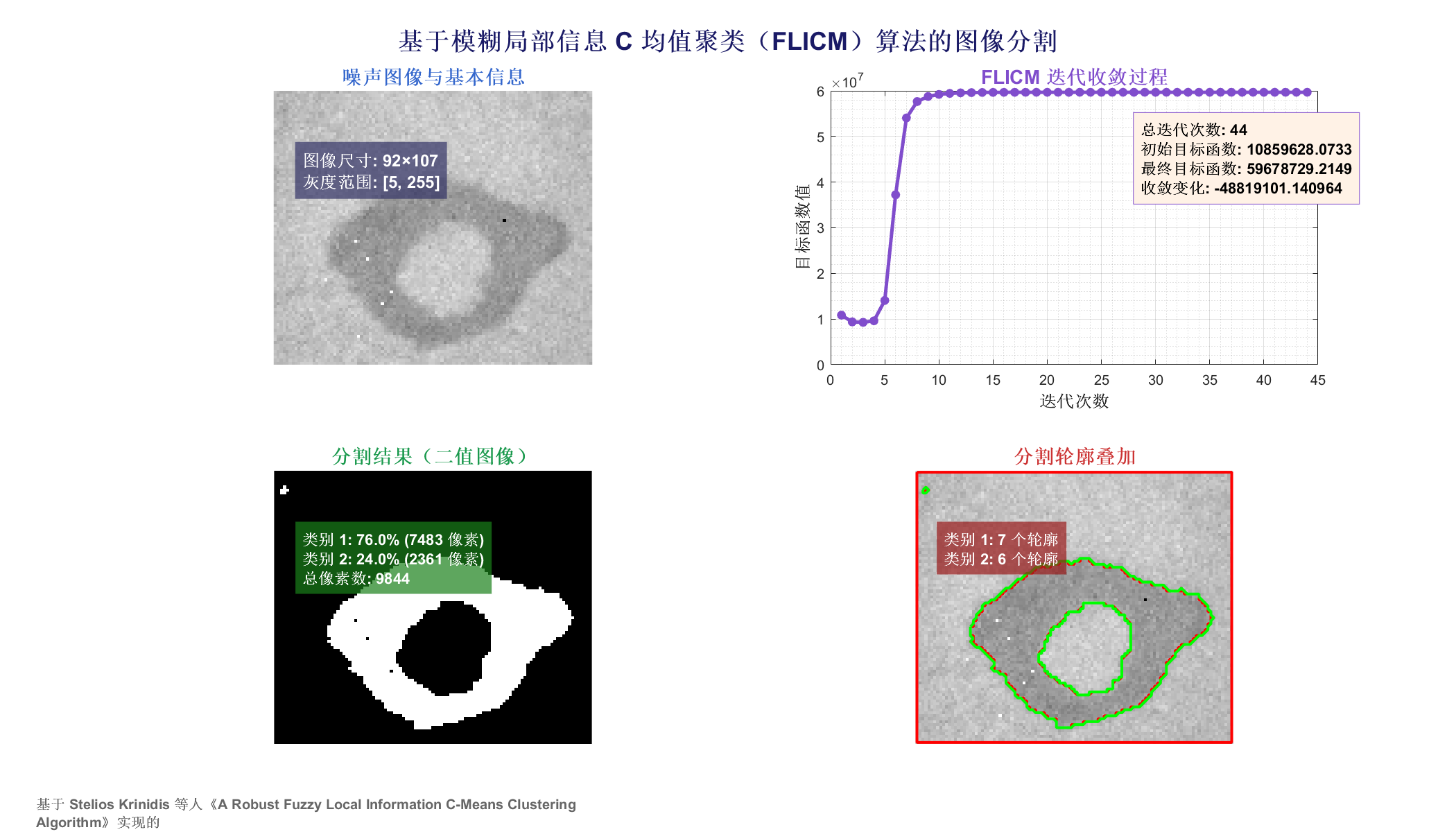
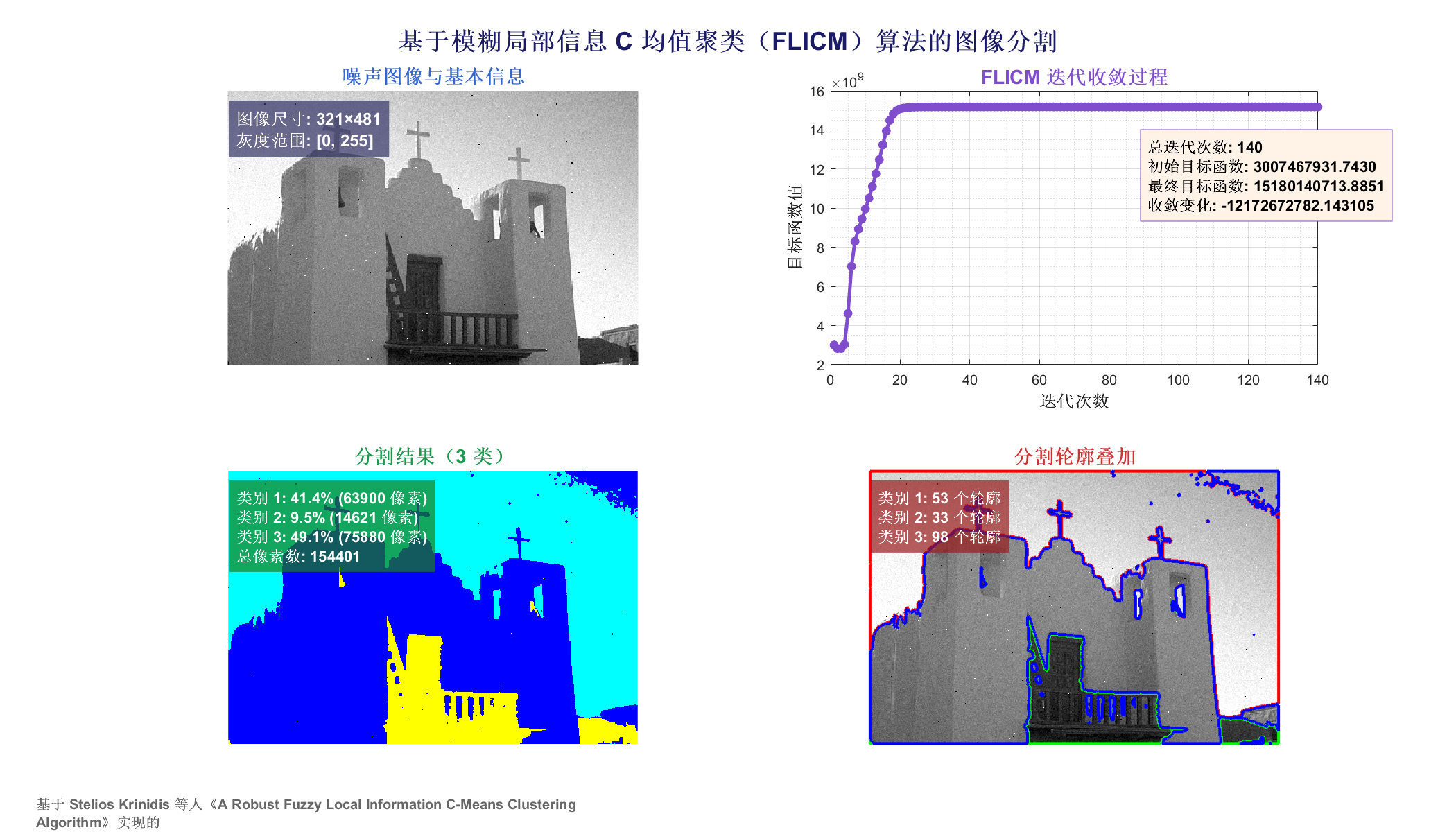
4 参考文献
1\] Krinidis S, Chatzis V. A robust fuzzy local information C-means clustering algorithm\[J\]. IEEE transactions on image processing, 2010, 19(5): 1328-1337. ## 5 MATLAB 代码 FLICM 作者已给出 c 语言编写的程序代码,已存放在工粽号(却相迎的小屋),诸君自取!