线性与非线性MPC控制的四旋翼轨迹跟踪仿真对比研究

线性与非线性MPC控制的四旋翼轨迹跟踪仿真对比研究【含说明文档】 [1]描述：利用已有的四旋翼运动学与动力学模型，建立MIMO状态空间模型，包括非线性模型与简化后的线性模型，并引入约束MPC控制，分别设计线性MPC控制器与非线性MPC控制器。 跟踪问题就是找到一个合适的控制输入，使得跟踪误差最小。 [2]说明文档内容： (1)基于状态空间模型预测控制器设计 (2)为了结合模型预测控制，将获得的四旋翼数学模型转化为状态空间模型 (3)基于四旋翼状态方程的线性MPC算法推导 (4)基于四旋翼非线性MPC算法推导 (5)线性MPC实现四旋翼路径跟踪仿真分析

在四旋翼飞行器的控制领域，轨迹跟踪是一个关键问题，而模型预测控制（MPC）是实现这一目标的有效手段。今天咱们就来深入探讨线性与非线性MPC控制在四旋翼轨迹跟踪中的仿真对比。

四旋翼运动学与动力学模型及状态空间模型建立

首先，我们要利用已有的四旋翼运动学与动力学模型，来构建MIMO（多输入多输出）状态空间模型。这里面包括非线性模型以及简化后的线性模型。

非线性模型

四旋翼的非线性动力学模型通常较为复杂，涉及到多个变量和非线性关系。以经典的牛顿 - 欧拉方程为基础，描述四旋翼在三维空间中的运动，比如位置（x,y,z）和姿态（\\phi,\\theta,\\psi），其力和力矩的平衡方程可以写成：

\[

\begin{cases}

m\ddot{x} = -T\sin\theta\cos\psi \\

m\ddot{y} = T\sin\theta\sin\psi \\

m\ddot{z} = T\cos\theta - mg \\

Ix\ddot{\phi} = (\tau{\phi} + I_{xz}(\dot{\theta}\dot{\psi}\cos\phi - \ddot{\theta}\sin\phi)) \\

Iy\ddot{\theta} = (\tau{\theta} + I_{xz}(\dot{\phi}\dot{\psi}\sin\phi + \ddot{\phi}\cos\phi)) \\

Iz\ddot{\psi} = \tau{\psi}

\end{cases}

\]

这里m是四旋翼的质量，T是总推力，\\tau*{\\phi},\\tau* {\\theta},\\tau*{\\psi}分别是滚转、俯仰和偏航力矩，I* x, I*y, I*z是转动惯量，I_{xz}是惯性积。这就是一个典型的非线性模型，它准确地描述了四旋翼的实际运动情况，但求解和控制设计相对复杂。

线性模型

为了简化控制设计，我们对非线性模型进行线性化处理。一般选择在平衡点附近进行线性化，假设在平衡点处姿态角都接近0，角速度也接近0。经过一系列数学推导（这里省略具体推导过程），可以得到线性化后的状态空间模型：

\[

\dot{\mathbf{x}} = \mathbf{A}\mathbf{x} + \mathbf{B}\mathbf{u}

\]

其中\\mathbf{x}是状态向量，包含位置、速度、姿态角和角速度等信息，\\mathbf{u}是控制输入向量，包含四个旋翼的转速，\\mathbf{A}和\\mathbf{B}是系统矩阵和输入矩阵。

基于状态空间模型预测控制器设计

模型预测控制的核心思想是利用系统的模型预测未来的输出，并通过优化控制输入使得预测输出尽可能跟踪期望轨迹，同时满足一定的约束条件。

结合模型预测控制，转化为状态空间模型

为了在MPC中使用，我们要将前面得到的四旋翼数学模型转化为适合MPC的状态空间模型形式。以线性模型为例，假设状态向量\\mathbf{x} = \[x, y, z, \\dot{x}, \\dot{y}, \\dot{z}, \\phi, \\theta, \\psi, \\dot{\\phi}, \\dot{\\theta}, \\dot{\\psi}\]\^T，控制输入向量\\mathbf{u} = \[\\omega*1\^2, \\omega* 2\^2, \\omega*3\^2, \\omega*4\^2\]\^T（\\omega_i是第i个旋翼的转速）。

基于四旋翼状态方程的线性MPC算法推导

线性MPC的目标是在每个采样时刻，求解一个有限时域的优化问题，以确定当前时刻的控制输入。假设预测时域为N*p，控制时域为N* c（N*c \\leq N*p）。

预测模型可以写成：

\[

\mathbf{X}{k+1|k} = \mathbf{A}\mathbf{X}{k|k} + \mathbf{B}\mathbf{U}_{k|k}

\]

其中\\mathbf{X}*{k\|k}是在k时刻对未来状态的预测，\\mathbf{U}*{k\|k}是在k时刻对未来控制输入的预测。

优化目标通常是最小化预测输出与期望轨迹之间的误差，加上对控制输入变化的惩罚，写成数学形式就是：

\[

J = \sum*{i = 1}^{N* p} (\mathbf{y}{k + i|k} - \mathbf{r} {k + i})^T\mathbf{Q}(\mathbf{y}{k + i|k} - \mathbf{r} {k + i}) + \sum*{i = 0}^{N* c - 1} \Delta\mathbf{u}{k + i|k}^T\mathbf{R}\Delta\mathbf{u}{k + i|k}

\]

这里\\mathbf{y}*{k + i\|k}是预测输出，\\mathbf{r}* {k + i}是期望轨迹，\\mathbf{Q}和\\mathbf{R}是权重矩阵，\\Delta\\mathbf{u}*{k + i\|k} = \\mathbf{u}*{k + i\|k} - \\mathbf{u}_{k + i - 1\|k}。

通过求解这个二次规划问题（QP），可以得到最优的控制输入序列\\mathbf{U}*{k\|k}\^*，通常只取序列中的第一个元素\\mathbf{u}*{k\|k}\^*作为当前时刻的实际控制输入。

以下是一个简单的Python代码示例，用于求解线性MPC中的QP问题（使用cvxpy库）：

import cvxpy as cp
import numpy as np

# 假设已经定义好A, B, Q, R, Np, Nc等参数
# 这里简单给出示例值
A = np.random.rand(12, 12)
B = np.random.rand(12, 4)
Q = np.eye(12)
R = np.eye(4)
Np = 10
Nc = 5

# 定义优化变量
U = cp.Variable((4, Nc))
X = cp.Variable((12, Np + 1))

# 定义约束条件
constraints = [X[:, 0] == x0]  # x0是当前状态
for i in range(Np):
    if i < Nc:
        constraints.append(X[:, i + 1] == A @ X[:, i] + B @ U[:, i])
    else:
        constraints.append(X[:, i + 1] == A @ X[:, i])

# 定义优化目标
cost = 0
for i in range(Np):
    cost += cp.quad_form(X[:, i] - r[i], Q)
for i in range(Nc):
    if i > 0:
        cost += cp.quad_form(U[:, i] - U[:, i - 1], R)
    else:
        cost += cp.quad_form(U[:, i], R)

# 求解优化问题
prob = cp.Problem(cp.Minimize(cost), constraints)
prob.solve()

# 获取最优控制输入
u_opt = U[:, 0].value

在这段代码中，首先定义了优化变量U（控制输入序列）和X（状态预测序列），然后根据预测模型和实际情况添加约束条件。接着定义优化目标cost，最后使用cvxpy库求解这个优化问题，得到最优的控制输入u_opt。

基于四旋翼非线性MPC算法推导

非线性MPC的原理与线性MPC类似，但由于模型是非线性的，优化问题不再是简单的二次规划问题，而是一个非线性规划问题（NLP）。

预测模型变为：

\[

\mathbf{X}{k+1|k} = f(\mathbf{X}{k|k}, \mathbf{U}_{k|k})

\]

其中f是非线性函数，由四旋翼的非线性动力学模型确定。

优化目标同样是最小化预测输出与期望轨迹之间的误差以及控制输入变化，形式与线性MPC类似：

\[

J = \sum*{i = 1}^{N* p} (\mathbf{y}{k + i|k} - \mathbf{r} {k + i})^T\mathbf{Q}(\mathbf{y}{k + i|k} - \mathbf{r} {k + i}) + \sum*{i = 0}^{N* c - 1} \Delta\mathbf{u}{k + i|k}^T\mathbf{R}\Delta\mathbf{u}{k + i|k}

\]

求解这个NLP问题通常比求解QP问题更复杂，需要使用一些专门的非线性优化算法，比如内点法等。由于代码实现相对复杂，这里暂不给出具体代码示例。

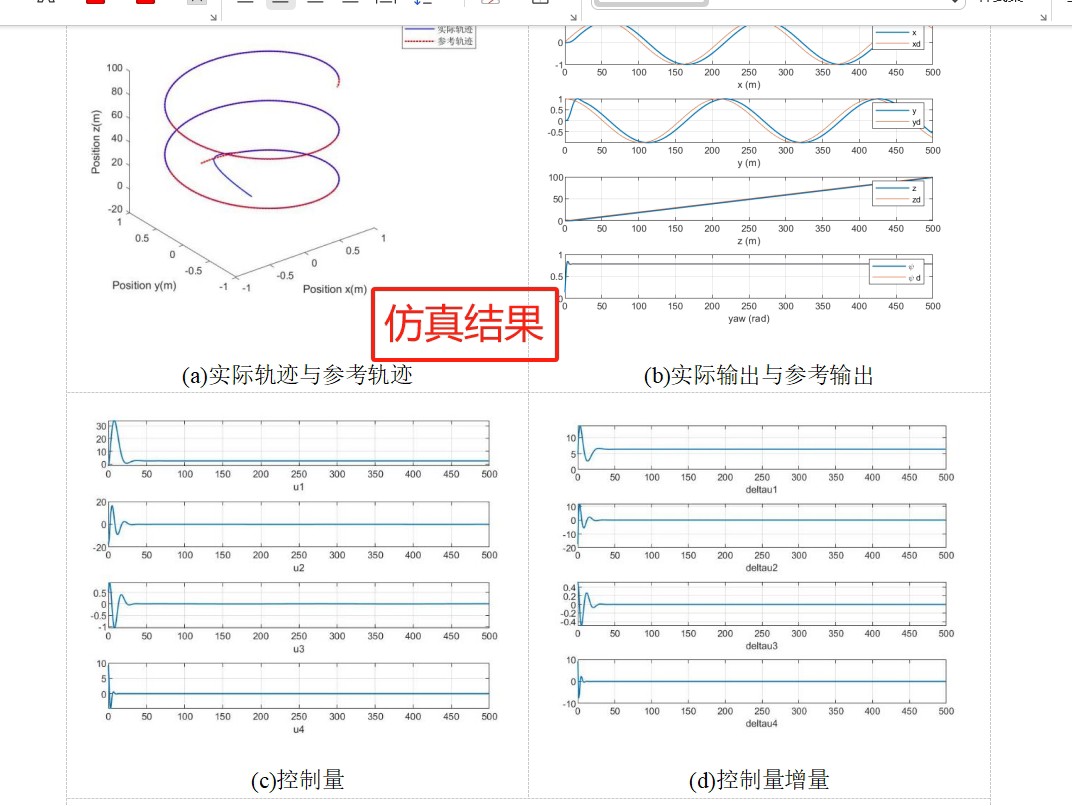
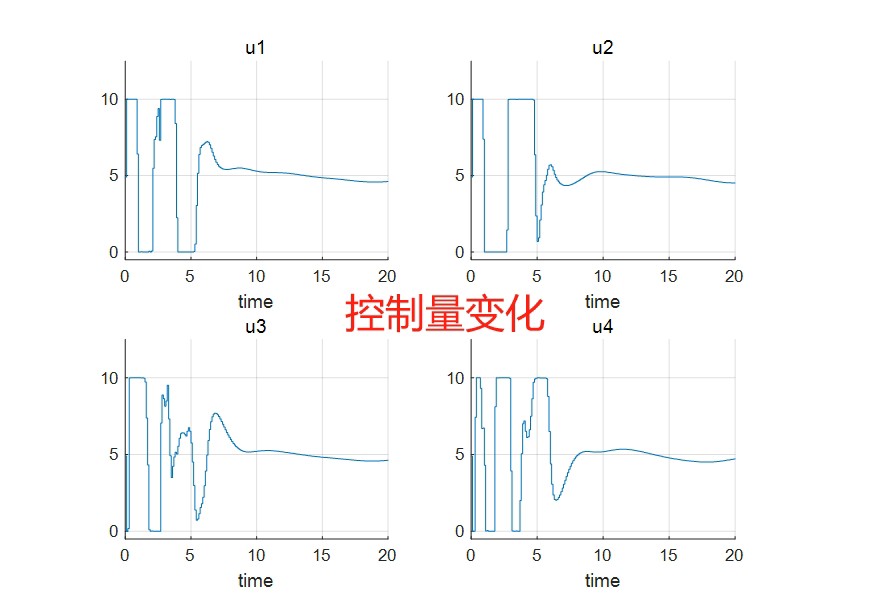
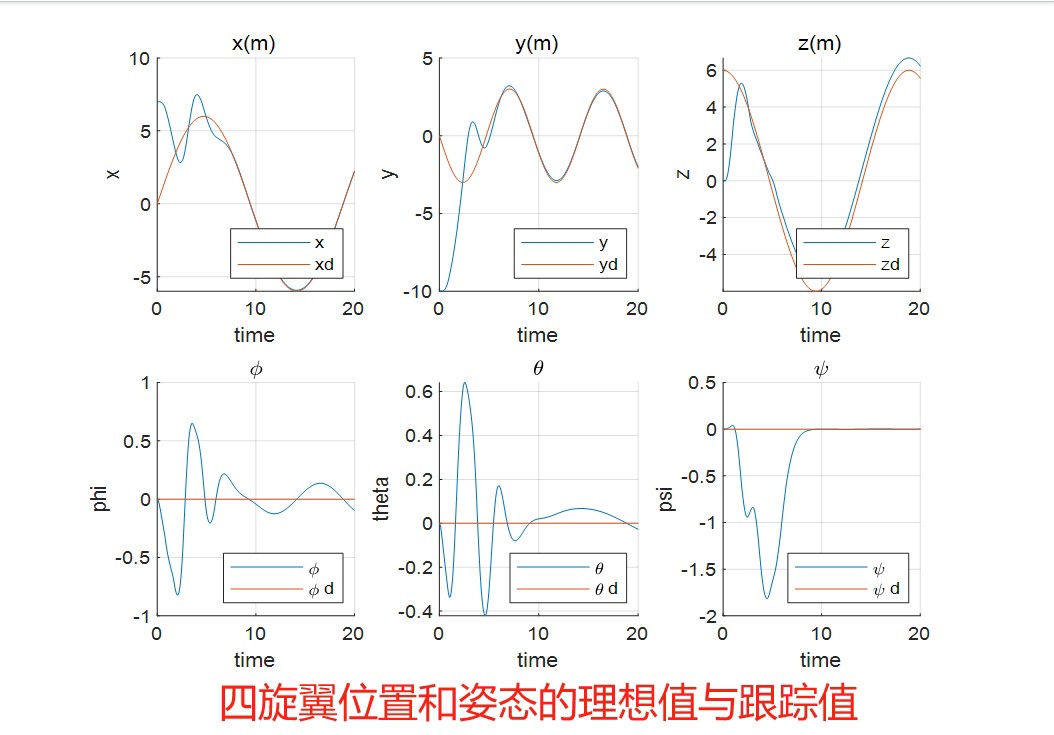
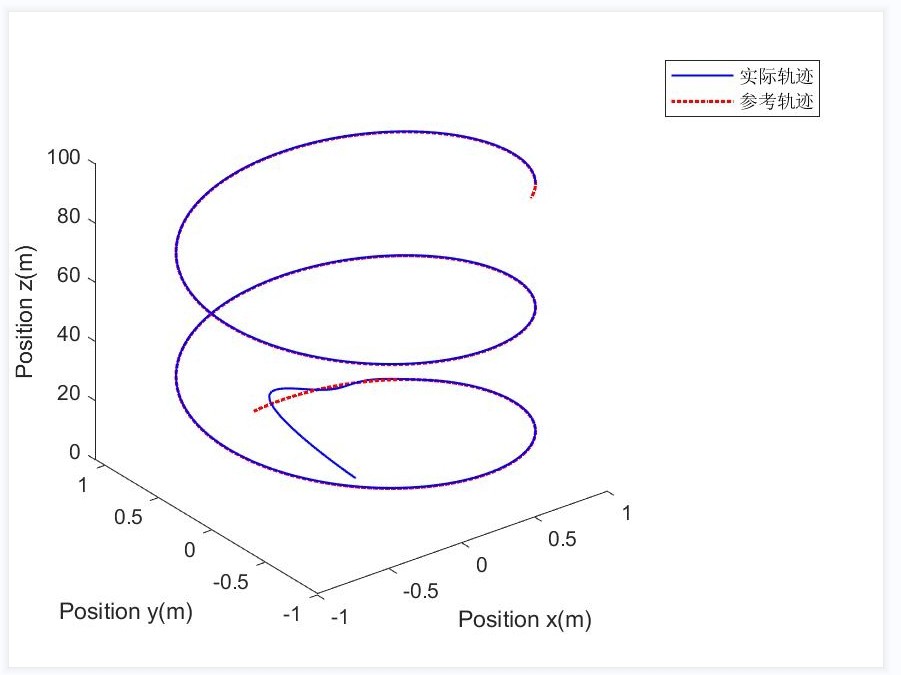
线性MPC实现四旋翼路径跟踪仿真分析

通过前面设计的线性MPC控制器，我们可以对四旋翼的路径跟踪进行仿真。在仿真中，设定期望轨迹，比如一个圆形轨迹或者一条直线轨迹，然后运行线性MPC算法，观察四旋翼的实际轨迹与期望轨迹的偏差。

在仿真过程中，我们可以调整一些参数，比如权重矩阵\\mathbf{Q}和\\mathbf{R}，观察它们对跟踪性能的影响。增大\\mathbf{Q}会更加注重跟踪误差的减小，使四旋翼更紧密地跟踪期望轨迹，但可能导致控制输入变化过于剧烈；增大\\mathbf{R}则会抑制控制输入的变化，使控制更加平滑，但可能会使跟踪误差略有增加。

通过对线性和非线性MPC控制的四旋翼轨迹跟踪仿真对比研究，我们可以更深入地了解两种控制方法的优缺点，为实际应用中的控制器选择提供有力的依据。

希望这篇文章能让大家对线性与非线性MPC控制在四旋翼轨迹跟踪中的应用有更清晰的认识，后续我们可以进一步探讨更多相关的优化和改进方法。