一、DFT基础与MATLAB实现原理
离散傅里叶变换(DFT)将有限长时域序列转换为频域表示,其数学定义为:
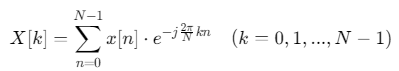
MATLAB通过内置函数fft高效实现DFT,其底层采用快速傅里叶变换(FFT)算法,时间复杂度为O(NlogN)O(NlogN)O(NlogN)。对于教学或原理验证,可手动实现DFT(时间复杂度O(N2)O(N^2)O(N2))。
二、MATLAB中DFT的两种实现方式
1. 使用内置函数fft(推荐)
matlab
% 生成测试信号(含噪声)
fs = 1000; % 采样率
t = 0:1/fs:1-1/fs; % 时间向量
x = sin(2*pi*50*t) + 0.5*sin(2*pi*120*t) + 0.3*randn(size(t)); % 50Hz+120Hz信号
% 计算DFT
N = length(x);
X = fft(x); % 直接调用FFT函数
% 频率轴计算
f = (0:N-1)*(fs/N); % 频率分辨率:fs/N
% 绘制频谱(单边幅值谱)
P2 = abs(X)/N; % 双边谱幅值
P1 = P2(1:N/2+1); % 单边谱
P1(2:end-1) = 2*P1(2:end-1); % 对称部分幅值加倍
figure;
plot(f, P1);
title('单边幅值谱');
xlabel('频率 (Hz)');
ylabel('幅值');2. 手动实现DFT(原理验证)
matlab
function X = my_dft(x)
N = length(x);
X = zeros(1, N);
for k = 0:N-1
for n = 0:N-1
X(k+1) = X(k+1) + x(n+1) * exp(-1j * 2 * pi * k * n / N);
end
end
end
% 测试手动实现
X_manual = my_dft(x);
figure;
subplot(2,1,1);
stem(abs(X_manual)/N);
title('手动实现DFT幅值谱');
subplot(2,1,2);
stem(abs(fft(x))/N);
title('FFT幅值谱');三、参数与结果分析
1. 频谱特性
- 对称性 :实信号DFT结果满足X[k]=X∗[N−k]X[k]=X∗[N−k]X[k]=X∗[N−k](共轭对称),虚部为零。
- 频率分辨率 :Δf=NfsΔf=Nf_sΔf=Nfs,由采样率和信号长度决定。
- 幅值修正 :
fft结果需除以信号长度N以匹配理论幅值。
2. 零填充(Zero Padding)
通过增加DFT点数提高频谱显示精度:
matlab
N_fft = 2048; % 填充到2048点
X_padded = fft(x, N_fft);
f_padded = (0:N_fft-1)*(fs/N_fft);
% 绘制填充后频谱
figure;
plot(f_padded, abs(X_padded)/N);
title('零填充后频谱');3. 窗函数应用
减少频谱泄漏(以汉宁窗为例):
matlab
window = hanning(N);
x_windowed = x .* window';
X_windowed = fft(x_windowed);
figure;
subplot(2,1,1);
plot(f, abs(X)/N);
title('无窗频谱');
subplot(2,1,2);
plot(f, abs(X_windowed)/N);
title('汉宁窗频谱');四、高级应用示例
1. 二维DFT(图像处理)
matlab
% 读取灰度图像
img = imread('lena.png');
img_gray = rgb2gray(img);
img_double = im2double(img_gray);
% 计算二维DFT
F = fft2(img_double);
F_shifted = fftshift(F); % 零频移到中心
% 显示频谱对数图
magnitude_spectrum = 20*log10(abs(F_shifted));
figure;
imshow(magnitude_spectrum);
title('图像频谱(对数尺度)');2. 相位解缠与重构
matlab
% 提取相位信息
phase = angle(fft(x));
% 相位解缠(简单示例)
phase_unwrapped = unwrap(phase);
% 仅用相位重构信号(需幅值信息)
X_recon = abs(fft(x)) .* exp(1j*phase_unwrapped);
x_recon = real(ifft(X_recon));参考代码 计算离散傅里叶变换dft www.youwenfan.com/contentcsn/84733.html
五、性能优化与注意事项
| 优化策略 | 实现方法 | 适用场景 |
|---|---|---|
| GPU加速 | 使用gpuArray转换数据 |
大规模数据(>1e6点) |
| 并行计算 | parfor循环处理多通道信号 |
多通道信号处理 |
| 内存优化 | 分块处理长信号(避免内存溢出) | 超长时域信号(>1e8点) |
注意事项:
- 索引从1开始:MATLAB中数组索引从1开始,需注意相位计算时的索引偏移。
- 复数精度:DFT结果包含实部和虚部,需完整保存。
- 频率轴对齐 :使用
fftshift将零频分量移到中心。
六、完整工程代码示例
matlab
% 文件:dft_analysis.m
clear; clc; close all;
%% 信号生成
fs = 1000; t = 0:1/fs:1-1/fs;
x = sin(2*pi*50*t) + 0.5*sin(2*pi*120*t) + 0.2*randn(size(t));
%% DFT计算
N = length(x);
X = fft(x);
f = (0:N-1)*(fs/N);
%% 单边谱绘制
P2 = abs(X)/N;
P1 = P2(1:N/2+1);
P1(2:end-1) = 2*P1(2:end-1);
figure;
plot(f, P1);
xlabel('频率 (Hz)');
ylabel('幅值');
title('单边幅值谱');
%% 相位分析
phase = angle(X);
figure;
stem(f, phase);
title('相位谱');
xlabel('频率 (Hz)');
ylabel('相位 (rad)');
%% 零填充演示
N_fft = 2048;
X_padded = fft(x, N_fft);
f_padded = (0:N_fft-1)*(fs/N_fft);
figure;
plot(f_padded, abs(X_padded)/N);
title('零填充后频谱');七、常见问题解答
Q1:DFT与FFT有何区别?
A:FFT是DFT的快速算法,计算复杂度从O(N2)降至O(NlogN),结果相同。
Q2:频谱中出现栅栏效应怎么办?
A:通过零填充(fft(x, N))提高频率分辨率,或使用加窗减少频谱泄漏。
Q3:如何从DFT结果中提取瞬时频率?
A:需结合短时傅里叶变换(STFT)或Hilbert变换,单帧DFT无法直接获取时变频率。