机器学习进阶＜6＞神奇的披萨店与学区房：走进RBFN的直觉世界

free-elcmacom2025-12-11 10:01

对于RBFN算法，在我之前的机器学习入门教程中已经有所提到。今天的这篇文章将是它的具象化与深入化的版本。

https://blog.csdn.net/2303_77568009/article/details/155580823?spm=1001.2014.3001.5501

第一部分：开场与引入------从分类的烦恼开始

1.1互动提问

想象你开了一家披萨店，现在想为顾客个性化推荐菜品。

你把每个顾客的**"甜口喜好度"和"咸口喜好度"**记录成坐标点。

比如(0.9, 0.1)是个超级甜食爱好者，(0.2, 0.8)是个咸味爱好者。

展示清晰的坐标系，X轴为甜口度(0-1)，Y轴为咸口度(0-1)。先展示几个明显分组的点。

下面我将使用Python语言实现上面所描述的画面：

python 复制代码 
import matplotlib.pyplot as plt
import numpy as np

# 设置中文字体和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 创建画布和子图
fig, ax = plt.subplots(figsize=(10, 8))

# 设置坐标轴范围和标签
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.set_xlabel('甜口喜好度', fontsize=12)
ax.set_ylabel('咸口喜好度', fontsize=12)
ax.set_title('披萨店顾客口味分布图', fontsize=14, fontweight='bold')

# 添加网格
ax.grid(True, linestyle='--', alpha=0.3)

# 生成模拟数据 - 三个明显的分组
np.random.seed(42)  # 设置随机种子以确保可重复性

# 组1: 甜食爱好者 (高甜度，低咸度)
sweet_lovers_x = np.random.normal(0.8, 0.08, 30)
sweet_lovers_y = np.random.normal(0.2, 0.08, 30)
sweet_lovers_x = np.clip(sweet_lovers_x, 0, 1)
sweet_lovers_y = np.clip(sweet_lovers_y, 0, 1)

# 组2: 咸味爱好者 (低甜度，高咸度)
salty_lovers_x = np.random.normal(0.2, 0.08, 30)
salty_lovers_y = np.random.normal(0.8, 0.08, 30)
salty_lovers_x = np.clip(salty_lovers_x, 0, 1)
salty_lovers_y = np.clip(salty_lovers_y, 0, 1)

# 组3: 甜咸适中者 (中等甜度和咸度)
balanced_x = np.random.normal(0.5, 0.1, 40)
balanced_y = np.random.normal(0.5, 0.1, 40)
balanced_x = np.clip(balanced_x, 0, 1)
balanced_y = np.clip(balanced_y, 0, 1)

# 绘制散点图
ax.scatter(sweet_lovers_x, sweet_lovers_y, color='red',
           s=100, alpha=0.7, edgecolors='darkred', linewidth=1.5,
           label='甜食爱好者')
ax.scatter(salty_lovers_x, salty_lovers_y, color='blue',
           s=100, alpha=0.7, edgecolors='darkblue', linewidth=1.5,
           label='咸味爱好者')
ax.scatter(balanced_x, balanced_y, color='green',
           s=100, alpha=0.7, edgecolors='darkgreen', linewidth=1.5,
           label='甜咸适中者')

# 添加示例点并标注
example_points = [
    (0.9, 0.1, "超级甜食爱好者", 'red'),
    (0.2, 0.8, "咸味爱好者", 'blue'),
    (0.5, 0.5, "甜咸适中", 'green'),
]

for x, y, label, color in example_points:
    ax.scatter(x, y, color=color, s=150, edgecolors='black',
               linewidth=2, zorder=5)
    ax.annotate(label, (x, y),
                xytext=(10, 10), textcoords='offset points',
                fontsize=10, fontweight='bold',
                bbox=dict(boxstyle='round,pad=0.3',
                         facecolor='white', alpha=0.8, edgecolor=color))

# 添加图例
ax.legend(loc='upper right', fontsize=10, framealpha=0.9)

# 在四个角落添加口味说明
ax.text(0.02, 0.98, '咸味爱好者区域', transform=ax.transAxes,
        fontsize=9, color='blue', alpha=0.7,
        bbox=dict(boxstyle='round', facecolor='white', alpha=0.7))
ax.text(0.02, 0.02, '清淡口味区域', transform=ax.transAxes,
        fontsize=9, color='gray', alpha=0.7,
        bbox=dict(boxstyle='round', facecolor='white', alpha=0.7))
ax.text(0.98, 0.98, '重口味区域', transform=ax.transAxes,
        fontsize=9, color='purple', alpha=0.7,
        bbox=dict(boxstyle='round', facecolor='white', alpha=0.7),
        ha='right')
ax.text(0.98, 0.02, '甜食爱好者区域', transform=ax.transAxes,
        fontsize=9, color='red', alpha=0.7,
        bbox=dict(boxstyle='round', facecolor='white', alpha=0.7),
        ha='right')

# 添加说明文本
ax.text(0.5, -0.08, '每个点代表一个顾客的甜咸口味偏好\n可以用直线划分不同口味区域',
        transform=ax.transAxes, ha='center', fontsize=10,
        bbox=dict(boxstyle='round', facecolor='lightyellow', alpha=0.8))

# 添加示例划分线（简单线性划分）
x_line = np.array([0, 1])
y_line = 1 - x_line  # 对角线
ax.plot(x_line, y_line, 'k--', alpha=0.5, linewidth=1.5, label='简单划分线')

# 调整布局
plt.tight_layout()

# 保存图片
plt.savefig('pizza_customer_taste_distribution.png', dpi=150, bbox_inches='tight')

# 显示图表
plt.show()

上述代码主要功能概述

这段Python代码使用matplotlib和numpy库生成了一张披萨店顾客口味偏好可视化分布图，主要用于教学演示RBFN（径向基函数网络）算法的引入部分。

上述代码执行的核心任务：

  1. 数据模拟生成：创建了三类模拟顾客数据

    • 甜食爱好者（红色点，高甜度低咸度）

    • 咸味爱好者（蓝色点，低甜度高咸度）

    • 甜咸适中者（绿色点，中等甜咸度）

  2. 可视化元素构建：

    • 设置了清晰坐标轴（甜口喜好度0-1，咸口喜好度0-1）

    • 使用不同颜色和大小区分三类顾客群体

    • 添加了关键示例点的详细标注

    • 绘制了简单的线性划分边界（对角线）

  3. 教学信息增强：

    • 四个角落添加了口味区域标注

    • 底部添加了说明文字

    • 使用图例清晰展示数据含义

上述代码生成的图片特征

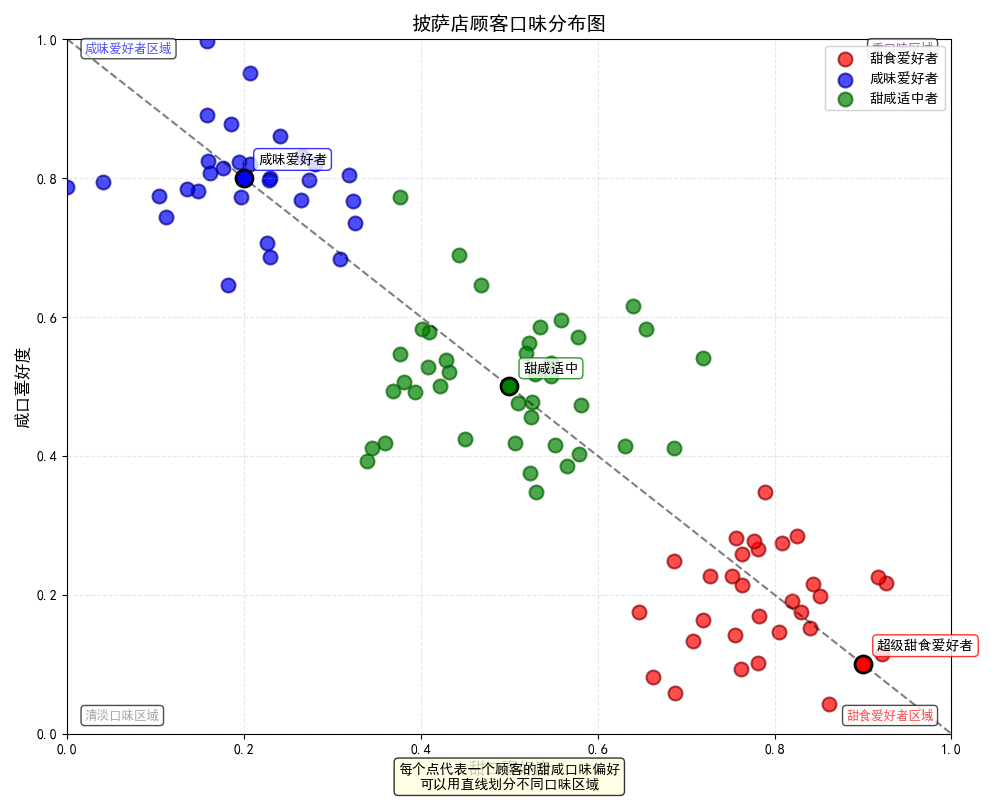
一张二维散点图，用于展示顾客在"甜咸口味"二维空间中的分布模式。

图片的视觉特征

（1）坐标系统

  • X轴：甜口喜好度（0-1，从左到右甜度增加）
  • Y轴：咸口喜好度（0-1，从下到上咸度增加）

（2）数据分布

  • 右下区域（红色点群）：甜食爱好者聚集区
  • 左上区域（蓝色点群）：咸味爱好者聚集区
  • 中间区域（绿色点群）：甜咸适中者

（3）关键标注点

  • (0.9, 0.1) - 超级甜食爱好者（红色突出标注）
  • (0.2, 0.8) - 咸味爱好者（蓝色突出标注）
  • (0.5, 0.5) - 甜咸适中（绿色突出标注）

（4）划分边界

  • 一条黑色虚线从(0,1)到(1,0)，展示了简单的线性分类方法

1.2提问1： 如果顾客分布像这样，你如何划分区域？

线性可分数据与划分：

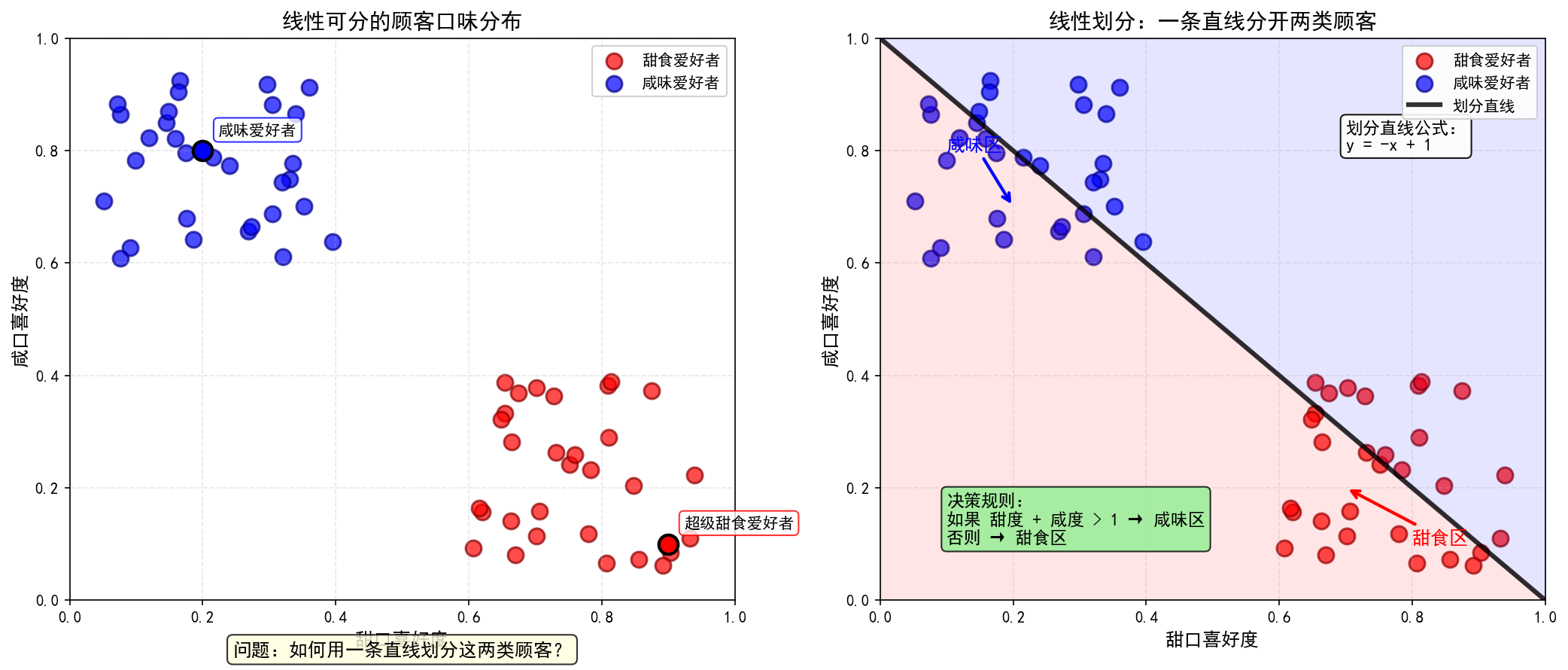
  • 左图：展示了两类线性可分的顾客数据（红点：甜食爱好者，蓝点：咸味爱好者）

  • 右图：展示了如何用一条直线（y = -x + 1）完美划分这两类顾客

  • 添加了区域填充、公式说明和决策规则，直观展示线性分类的思想

所使用到的代码

python 复制代码 
import matplotlib.pyplot as plt
import numpy as np

# 设置中文字体和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 创建画布和子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# 第一部分：生成线性可分的数据
np.random.seed(42)

# 组1: 甜食爱好者 (甜度高，咸度低)
sweet_lovers_x = np.random.uniform(0.6, 0.95, 30)
sweet_lovers_y = np.random.uniform(0.05, 0.4, 30)

# 组2: 咸味爱好者 (甜度低，咸度高)
salty_lovers_x = np.random.uniform(0.05, 0.4, 30)
salty_lovers_y = np.random.uniform(0.6, 0.95, 30)

# 绘制第一个图：线性可分的数据点
ax1.set_xlim(0, 1)
ax1.set_ylim(0, 1)
ax1.set_xlabel('甜口喜好度', fontsize=12)
ax1.set_ylabel('咸口喜好度', fontsize=12)
ax1.set_title('线性可分的顾客口味分布', fontsize=14, fontweight='bold')
ax1.grid(True, linestyle='--', alpha=0.3)

# 绘制散点图
ax1.scatter(sweet_lovers_x, sweet_lovers_y, color='red',
            s=100, alpha=0.7, edgecolors='darkred', linewidth=1.5,
            label='甜食爱好者')
ax1.scatter(salty_lovers_x, salty_lovers_y, color='blue',
            s=100, alpha=0.7, edgecolors='darkblue', linewidth=1.5,
            label='咸味爱好者')

# 添加示例点标注
example_points = [
    (0.9, 0.1, "超级甜食爱好者", 'red'),
    (0.2, 0.8, "咸味爱好者", 'blue'),
]

for x, y, label, color in example_points:
    ax1.scatter(x, y, color=color, s=150, edgecolors='black',
                linewidth=2, zorder=5)
    ax1.annotate(label, (x, y),
                 xytext=(10, 10), textcoords='offset points',
                 fontsize=10, fontweight='bold',
                 bbox=dict(boxstyle='round,pad=0.3',
                          facecolor='white', alpha=0.8, edgecolor=color))

# 添加问题文本
ax1.text(0.5, -0.1, '问题：如何用一条直线划分这两类顾客？',
         transform=ax1.transAxes, ha='center', fontsize=12,
         bbox=dict(boxstyle='round', facecolor='lightyellow', alpha=0.8))

# 第二部分：展示线性划分
ax2.set_xlim(0, 1)
ax2.set_ylim(0, 1)
ax2.set_xlabel('甜口喜好度', fontsize=12)
ax2.set_ylabel('咸口喜好度', fontsize=12)
ax2.set_title('线性划分：一条直线分开两类顾客', fontsize=14, fontweight='bold')
ax2.grid(True, linestyle='--', alpha=0.3)

# 绘制相同的散点图
ax2.scatter(sweet_lovers_x, sweet_lovers_y, color='red',
            s=100, alpha=0.7, edgecolors='darkred', linewidth=1.5,
            label='甜食爱好者')
ax2.scatter(salty_lovers_x, salty_lovers_y, color='blue',
            s=100, alpha=0.7, edgecolors='darkblue', linewidth=1.5,
            label='咸味爱好者')

# 计算并绘制最佳分割线（线性可分数据的简单分隔线）
# 我们使用一条对角线作为分隔线：y = -x + 1
x_line = np.linspace(0, 1, 100)
y_line = 1 - x_line  # 对角线，将空间分为两个区域

# 绘制分隔线
ax2.plot(x_line, y_line, 'k-', linewidth=3, alpha=0.8, label='划分直线')

# 添加箭头说明分隔线的方向
ax2.annotate('甜食区', xy=(0.7, 0.2), xytext=(0.8, 0.1),
             arrowprops=dict(arrowstyle='->', lw=2, color='red'),
             fontsize=12, fontweight='bold', color='red')
ax2.annotate('咸味区', xy=(0.2, 0.7), xytext=(0.1, 0.8),
             arrowprops=dict(arrowstyle='->', lw=2, color='blue'),
             fontsize=12, fontweight='bold', color='blue')

# 填充区域（可选，更直观）
# 甜食区填充（线下区域）
ax2.fill_between(x_line, 0, y_line, alpha=0.1, color='red')
# 咸味区填充（线上区域）
ax2.fill_between(x_line, y_line, 1, alpha=0.1, color='blue')

# 添加公式说明
ax2.text(0.7, 0.8, '划分直线公式：\ny = -x + 1',
         fontsize=11, bbox=dict(boxstyle='round', facecolor='white', alpha=0.9))

# 添加决策规则说明
ax2.text(0.1, 0.1, '决策规则：\n如果 甜度 + 咸度 > 1 → 咸味区\n否则 → 甜食区',
         fontsize=11, bbox=dict(boxstyle='round', facecolor='lightgreen', alpha=0.8))

# 添加图例
ax1.legend(loc='upper right', fontsize=10, framealpha=0.9)
ax2.legend(loc='upper right', fontsize=10, framealpha=0.9)

# 调整布局
plt.tight_layout()

# 保存图片
plt.savefig('pizza_customer_linear_separable.png', dpi=150, bbox_inches='tight')

# 显示图表
plt.show()

1.3提问2： 现在看看真实情况------甜口党和咸口党不是简单分开，而是甜咸适中的人围成一圈，极端口味的人在中间。还能用一条直线分开吗？

非线性数据示例：

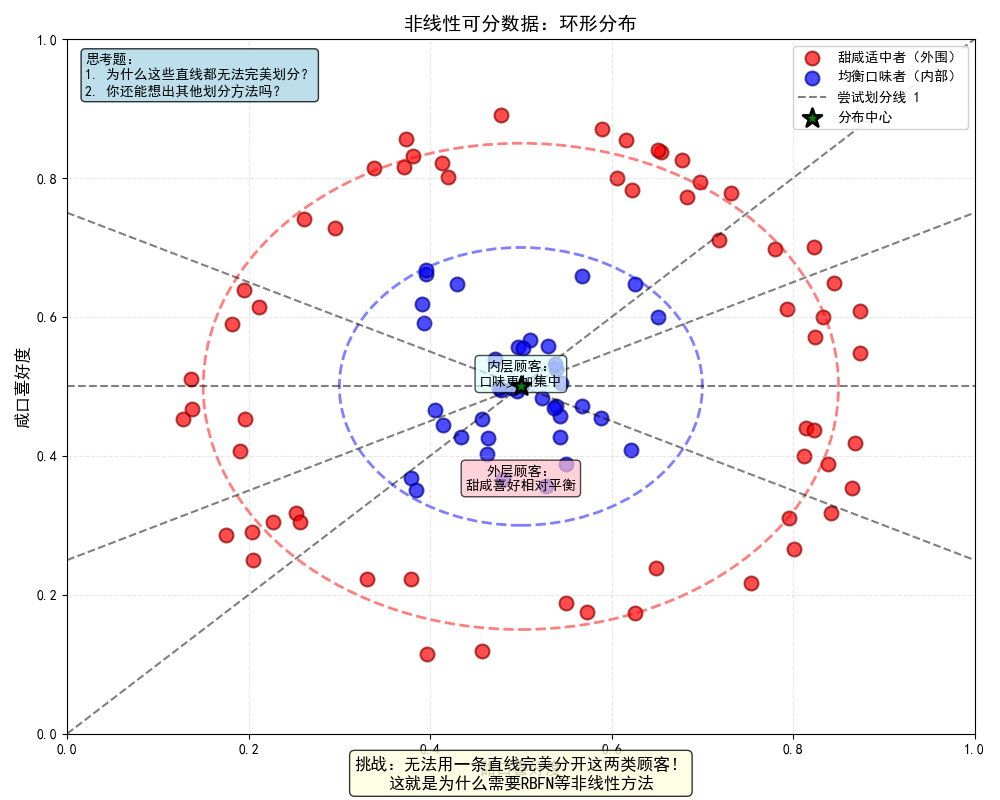
  1. 展示了环形分布数据（红点在外圈，蓝点在内圈）

  2. 画了多条直线，展示无论如何都无法用一条直线完美划分

  3. 我们会发现："一条直线无法描述这种'抱团'关系"

  • 代码：
python 复制代码 
import matplotlib.pyplot as plt
import numpy as np

# 设置中文字体和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 创建画布
fig, ax = plt.subplots(figsize=(10, 8))

# 生成环形分布数据（非线性不可分）
np.random.seed(42)

# 外圈：甜咸适中者（外围环形分布）
theta = np.random.uniform(0, 2*np.pi, 60)  # 60个角度
radius = np.random.uniform(0.3, 0.4, 60)   # 半径在0.3-0.4之间
x_circle = 0.5 + radius * np.cos(theta)
y_circle = 0.5 + radius * np.sin(theta)

# 内圈：均衡口味者（内部聚集分布）
radius_inner = np.random.uniform(0, 0.2, 40)   # 半径在0-0.2之间
theta_inner = np.random.uniform(0, 2*np.pi, 40)  # 40个角度
x_inner = 0.5 + radius_inner * np.cos(theta_inner)
y_inner = 0.5 + radius_inner * np.sin(theta_inner)

# 设置坐标轴范围和标签
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.set_xlabel('甜口喜好度', fontsize=12)
ax.set_ylabel('咸口喜好度', fontsize=12)
ax.set_title('非线性可分数据：环形分布', fontsize=14, fontweight='bold')
ax.grid(True, linestyle='--', alpha=0.3)

# 绘制环形分布
ax.scatter(x_circle, y_circle, color='red',
           s=100, alpha=0.7, edgecolors='darkred', linewidth=1.5,
           label='甜咸适中者（外围）')
ax.scatter(x_inner, y_inner, color='blue',
           s=100, alpha=0.7, edgecolors='darkblue', linewidth=1.5,
           label='均衡口味者（内部）')

# 尝试画几条直线，展示线性划分的困难
# 画4条不同角度的直线
for i in range(4):
    angle = i * np.pi / 4  # 0°, 45°, 90°, 135°
    x_line = np.array([0, 1])
    y_line = 0.5 + 0.5 * np.tan(angle) * (x_line - 0.5)
    # 截断到[0,1]范围内
    y_line = np.clip(y_line, 0, 1)
    ax.plot(x_line, y_line, 'k--', alpha=0.5, linewidth=1.5,
            label=f'尝试划分线 {i+1}' if i == 0 else "")

# 添加中心点（数据分布的中心）
ax.scatter(0.5, 0.5, color='green', s=200, marker='*',
           edgecolors='black', linewidth=2, zorder=5,
           label='分布中心')

# 添加环形区域的示意性圆圈
circle_outer = plt.Circle((0.5, 0.5), 0.35, color='red',
                          fill=False, linestyle='--', linewidth=2, alpha=0.5)
circle_inner = plt.Circle((0.5, 0.5), 0.2, color='blue',
                          fill=False, linestyle='--', linewidth=2, alpha=0.5)
ax.add_patch(circle_outer)
ax.add_patch(circle_inner)

# 添加说明文本
ax.text(0.5, -0.08, '挑战：无法用一条直线完美分开这两类顾客！\n这就是为什么需要RBFN等非线性方法',
        transform=ax.transAxes, ha='center', fontsize=12,
        bbox=dict(boxstyle='round', facecolor='lightyellow', alpha=0.8))

# 添加问题思考框
ax.text(0.02, 0.98, '思考题：\n1. 为什么这些直线都无法完美划分？\n2. 你还能想出其他划分方法吗？',
        transform=ax.transAxes, fontsize=10,
        bbox=dict(boxstyle='round', facecolor='lightblue', alpha=0.8),
        verticalalignment='top')

# 添加关键观察点
ax.text(0.5, 0.35, '外层顾客：\n甜咸喜好相对平衡',
        ha='center', fontsize=10,
        bbox=dict(boxstyle='round', facecolor='pink', alpha=0.7))
ax.text(0.5, 0.5, '内层顾客：\n口味更加集中',
        ha='center', fontsize=10,
        bbox=dict(boxstyle='round', facecolor='lightcyan', alpha=0.7))

# 添加图例
ax.legend(loc='upper right', fontsize=10, framealpha=0.9)

# 调整布局
plt.tight_layout()

# 保存图片
plt.savefig('pizza_customer_nonlinear.png', dpi=150, bbox_inches='tight')

# 显示图表
plt.show()

print("图片已生成：pizza_customer_nonlinear.png")
print("\n图片说明：")
print("1. 展示了环形分布的非线性数据，红点在外圈，蓝点在内圈")
print("2. 画了4条不同方向的直线，展示无论直线怎么画都无法完美划分")
print("3. 添加了圆形示意线，帮助理解数据的分布模式")
print("4. 为引入RBFN等非线性分类方法提供直观的视觉案例")

【认知冲突升级】

展示更复杂的"双月牙形"数据：
如果数据像两个交错的月牙呢？一个团是喜欢甜咸搭配的，另一个是喜欢单一口味的。

直线还能解决吗？

如下图所示：

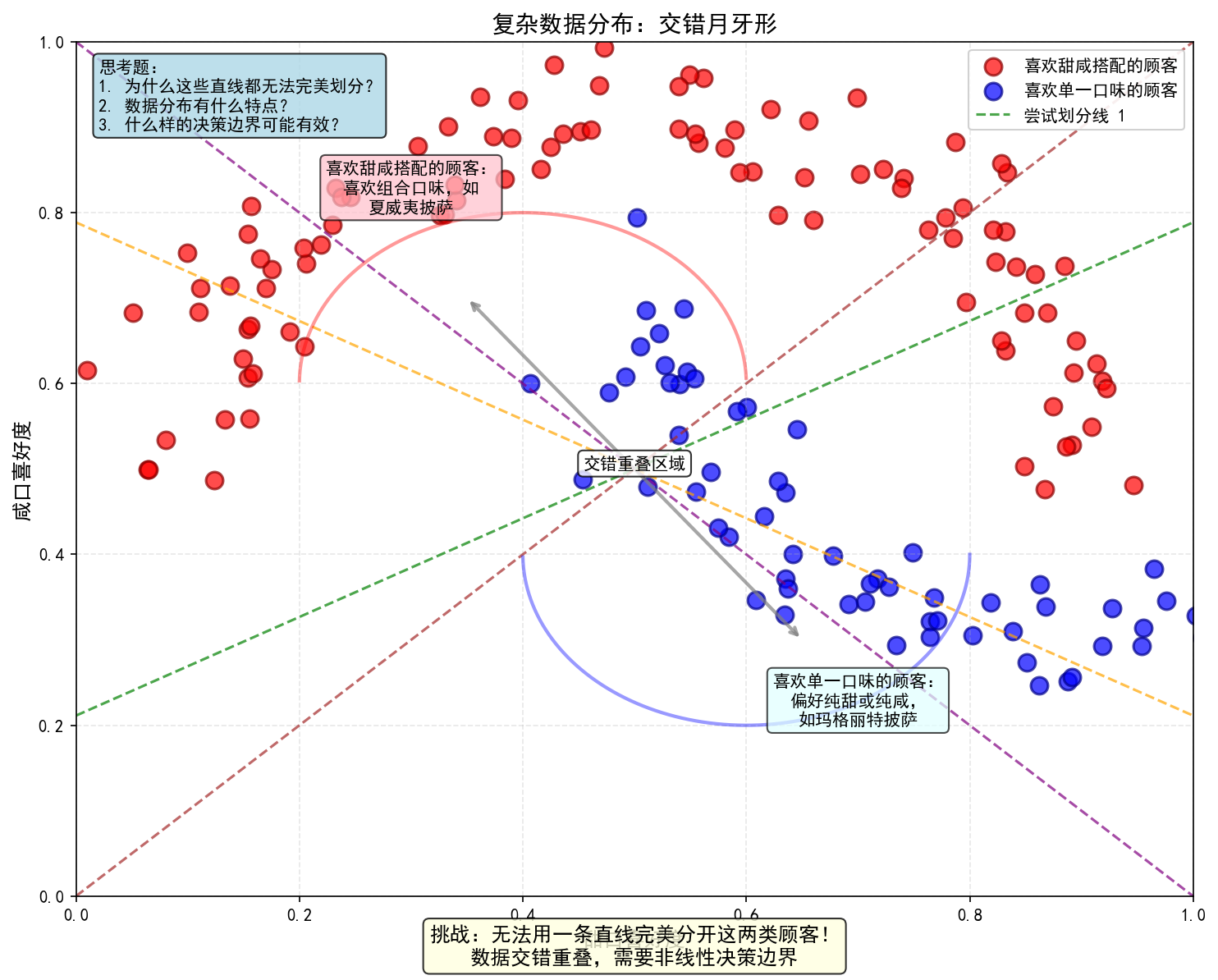
这张图片展示了交错月牙形的非线性数据分布，具体特征包括：

数据分布

  • 红色点：喜欢甜咸搭配的顾客（形成一个月牙形）

  • 蓝色点：喜欢单一口味的顾客（形成另一个交错月牙形）

  • 数据特点：两个月牙形相互交错，形成复杂的分布模式

视觉元素

  • 4条不同颜色的直线：展示尝试用线性方法划分的失败

  • 月牙形轮廓：用半透明线条示意数据的实际分布模式

  • 交错箭头：直观展示两类数据的交错关系

  • 多个说明文本框：解释数据特点和问题挑战

这里告诉了我们下面这些道理：

  • 简单线性可分数据 vs. 复杂非线性数据

  • 线性分类器的局限性

  • 为什么需要RBFN等非线性方法

1.4引出主题与类比

生活化比喻：

这些抱团的数据点，让我们想到现实中的什么现象？

答案是：学区房！

下面是一张热力图：学校位置为热点中心，房价随距离衰减。

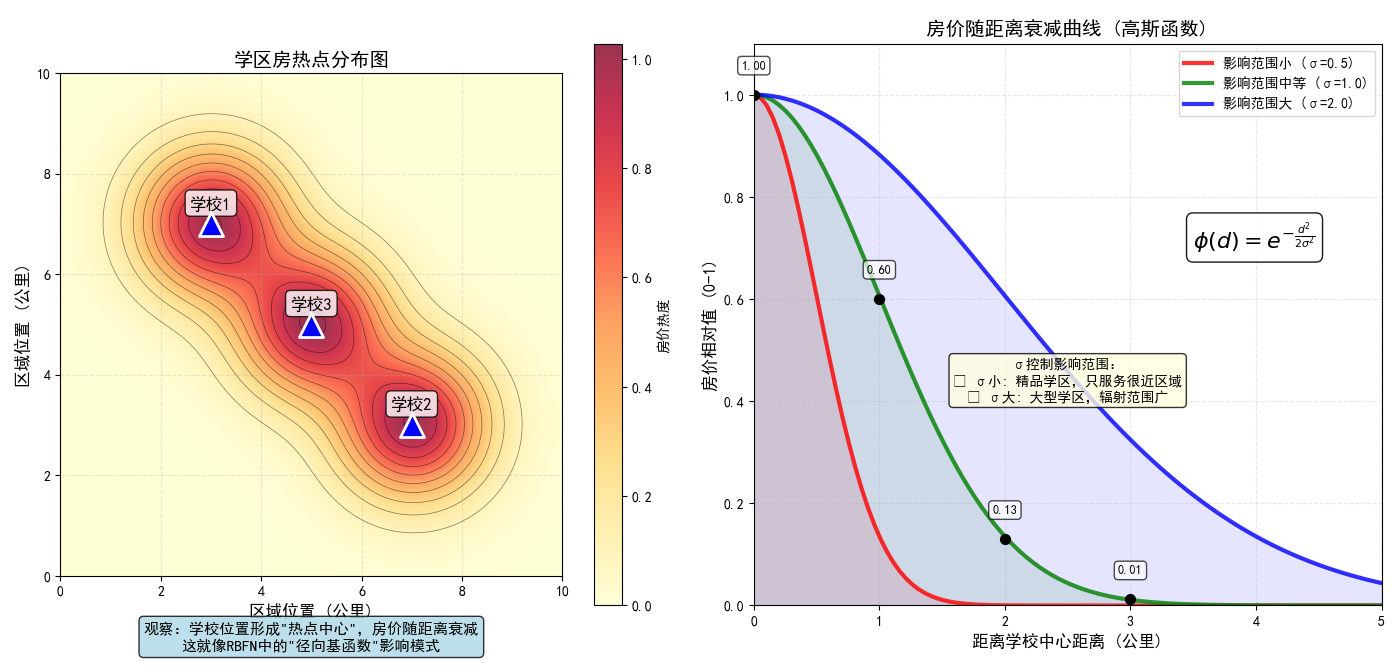
这张图完美展示了RBFN的核心思想：通过多个"中心点"和"距离衰减"模式来建模复杂的数据关系。

上图说明

左图：学区房热点分布热力图

  1. 三个学校热点中心：蓝色三角形标记三个学校位置

  2. 热力分布 ：颜色从红色（高房价）到黄色（中等）再到浅色（低房价）

  3. 等值线：显示房价的梯度变化，直观展示"随距离衰减"

  4. 核心观察：学校形成明显的"热点中心"，影响周围的房价分布

右图：房价随距离衰减曲线

  1. 三条衰减曲线：展示不同σ参数（影响范围）下的衰减模式

    • 红色：σ=0.5，影响范围小（精品学区）

    • 绿色：σ=1.0，影响范围中等（普通学区）

    • 蓝色：σ=2.0，影响范围大（大型学区）

  2. 数学公式 ：φ(d) = exp(-d²/(2σ²))，即RBFN中的高斯函数

  3. 关键点标注：显示在特定距离下的房价相对值

1.5RBFN类比总结

|-----------|------------|--------------|
| 学区房现象 | RBFN组件 | 功能类比 |
| 学校位置 | 中心点 | 数据空间中的"热点"位置 |
| 房价分布 | 径向基函数输出 | 基于距离的影响力值 |
| 距离学校远近 | 欧氏距离计算 | 输入点到中心点的距离 |
| 学校规模大小 | 宽度参数σ | 影响范围的大小 |
| 多个学校影响叠加 | 多个RBF单元输出 | 隐层多个神经元的激活值 |
| 最终房价决定 | 输出层加权和 | 总部汇总各分店意见 |

  1. 抽象的RBFN概念与现实的学区房

  2. 理解中心点：学校位置对应RBFN中的中心点

  3. 理解影响力函数：房价随距离衰减对应径向基函数

  4. 理解参数σ：不同规模的学校对应不同的σ值

  5. 理解多个中心叠加：多个学校共同影响整个区域的房价，就像RBFN中多个隐层单元共同决定输出

比喻展开：

  1. 每个学校就是一个热点中心

  2. 离学校越近，房价越高：但不是直线下降，而是快速上升到一个峰值后逐渐下降

  3. 多个学校就形成多个热点区域，共同决定整个城市的房价分布

1.6核心类比全景展示

|------------|-------------|---------------|
| 现实世界 | RBFN组件 | 功能类比 |
| 披萨连锁公司 | 整个RBFN网络 | 一个完整的决策系统 |
| 城市里的黄金店址 | 隐层神经元的中心点 | 数据空间中的"热点位置" |
| 披萨分店 | 一个RBF单元 | 专门服务某个区域的"专家" |
| 门店影响力范围 | 径向基函数（高斯函数） | 影响力的计算方式 |
| 配送范围半径 | 宽度参数σ | 门店的服务范围大小 |
| 公司总部 | 输出层 | 汇总所有分店意见做最终决策 |
| 分店对总部的汇报权重 | 连接权重w | 每个分店在决策中的话语权 |

那么这个智能披萨连锁系统是如何工作的呢？它有三件法宝！

第二部分：三大法宝：找中心、量距离、算影响（核心思想）

法宝一：找中心------我们的"披萨店"开在哪？

在陌生城市开分店，第一步是什么？

答案：找人流密集区。

对于数据来说，就是找数据点密集区。

  1. 初始状态：展示散乱的数据点（用不同颜色区分潜在类别）

  2. 第一步：随机选址：随机放置K个"店铺标志"（初始中心点），用不同形状标记

  3. 第二步：分配顾客：动画显示每个数据点奔向最近的店铺，"这个顾客归你管！"

  4. 第三步：重新选址：店铺说："我的顾客都在这片，我应该搬到他们的中心位置！"------中心点移动到簇的中心

  5. 第四步：重新分配：由于店铺移动，有些顾客要"重新选择店铺"

  6. 循环至稳定：展示2-3轮迭代，直到中心点不再移动

下面是我使用k-means算法复现1-6的过程的图片：

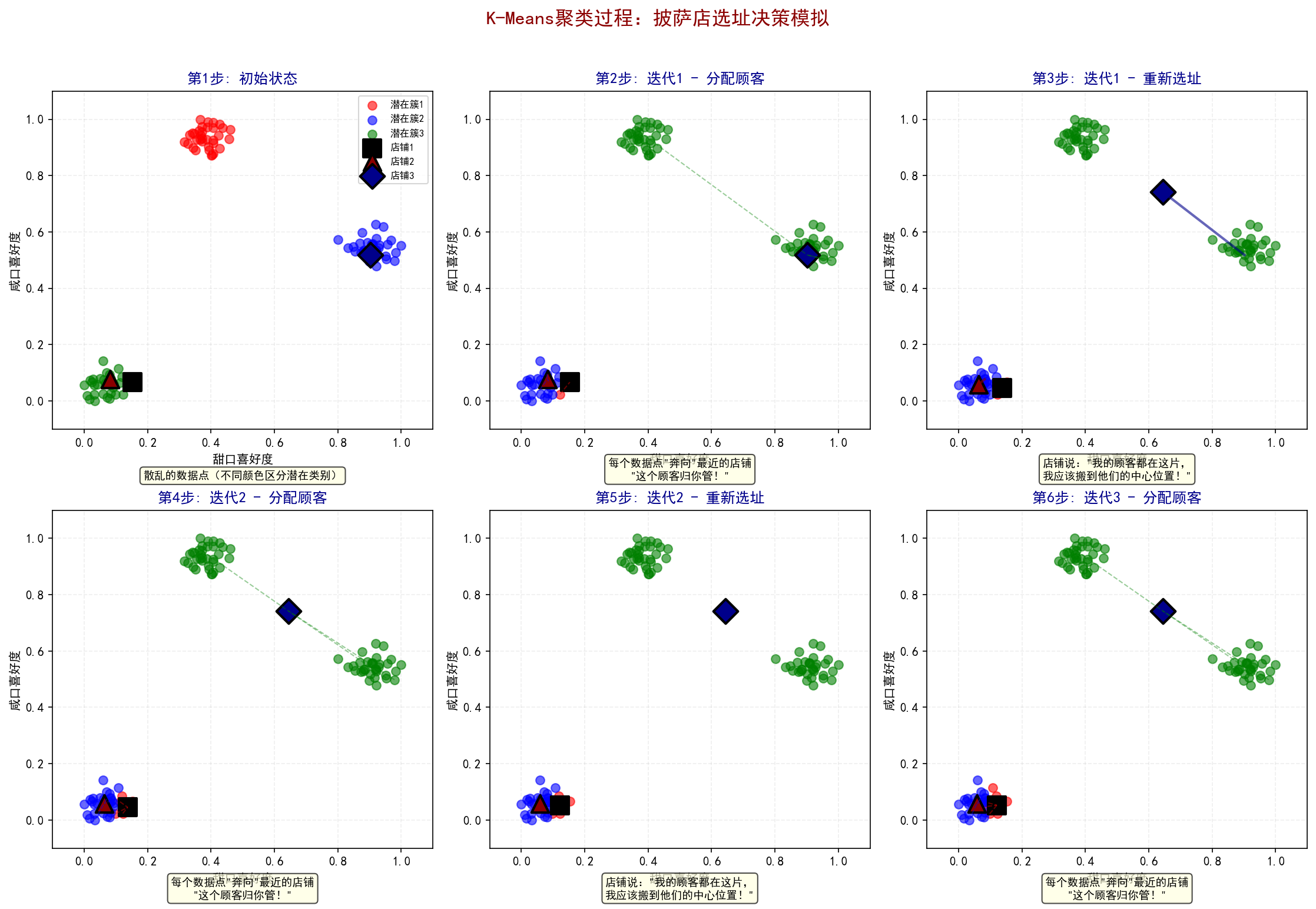
如果没有学习过k-means算法，可以阅读这篇文章，希望它能够帮助你快速理解k-means算法：

https://blog.csdn.net/2303_77568009/article/details/155718712?spm=1001.2014.3001.5502

所涉及到的代码：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# 设置中文字体和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 生成模拟数据
np.random.seed(42)
n_samples = 100
n_clusters = 3

# 生成三个簇的数据
X, y_true = make_blobs(n_samples=n_samples, centers=n_clusters,
                       cluster_std=0.6, random_state=42)

# 对数据进行缩放，使其在[0,1]范围内
X = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))


# K-Means算法实现（简化版，固定迭代4次）
def kmeans_step_by_step(X, n_clusters=3, max_iter=4):
    n_samples, n_features = X.shape

    # 记录每一步的状态
    history = []

    # 第一步：随机初始化中心点
    np.random.seed(42)
    indices = np.random.choice(n_samples, n_clusters, replace=False)
    centers = X[indices].copy()

    # 记录初始状态
    history.append({
        'centers': centers.copy(),
        'labels': None,
        'step': '初始状态',
        'description': '散乱的数据点（不同颜色区分潜在类别）'
    })

    # 迭代过程
    for iteration in range(max_iter):
        # 分配点到最近的中心点
        distances = np.sqrt(((X[:, np.newaxis, :] - centers[np.newaxis, :, :]) ** 2).sum(axis=2))
        labels = np.argmin(distances, axis=1)

        # 记录分配状态
        history.append({
            'centers': centers.copy(),
            'labels': labels.copy(),
            'step': f'迭代{iteration + 1} - 分配顾客',
            'description': f'每个数据点"奔向"最近的店铺\n"这个顾客归你管！"'
        })

        # 重新计算中心点
        new_centers = np.zeros_like(centers)
        for k in range(n_clusters):
            if np.sum(labels == k) > 0:
                new_centers[k] = X[labels == k].mean(axis=0)
            else:
                new_centers[k] = centers[k]

        # 记录重新选址状态
        history.append({
            'centers': new_centers.copy(),
            'labels': labels.copy(),
            'step': f'迭代{iteration + 1} - 重新选址',
            'description': f'店铺说："我的顾客都在这片，\n我应该搬到他们的中心位置！"'
        })

        # 检查收敛
        if np.allclose(centers, new_centers, rtol=1e-4):
            break

        centers = new_centers

    return history, X


# 执行K-Means算法并获取历史状态
history, X = kmeans_step_by_step(X, n_clusters=3, max_iter=3)

# 创建颜色映射
cluster_colors = ['red', 'blue', 'green', 'orange', 'purple']
center_markers = ['s', '^', 'D']  # 正方形、三角形、菱形
center_colors = ['black', 'darkred', 'darkblue']

# 创建子图展示K-Means过程
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.flatten()

# 确保我们只绘制实际存在的步骤
num_steps = min(len(history), len(axes))

for idx in range(num_steps):
    state = history[idx]
    ax = axes[idx]

    # 绘制所有数据点
    if state['labels'] is None:
        # 初始状态，用不同颜色表示潜在的簇（基于真实标签）
        unique_labels = np.unique(y_true)
        for k in unique_labels:
            mask = (y_true == k)
            ax.scatter(X[mask, 0], X[mask, 1],
                       color=cluster_colors[k % len(cluster_colors)],
                       alpha=0.6, s=50, label=f'潜在簇{k + 1}')
    else:
        # 分配后的状态，用不同颜色表示簇
        for k in range(n_clusters):
            mask = state['labels'] == k
            if np.any(mask):
                ax.scatter(X[mask, 0], X[mask, 1],
                           color=cluster_colors[k % len(cluster_colors)],
                           alpha=0.6, s=50, label=f'簇{k + 1}的顾客')

    # 绘制中心点
    for k, center in enumerate(state['centers']):
        ax.scatter(center[0], center[1],
                   color=center_colors[k % len(center_colors)],
                   marker=center_markers[k % len(center_markers)],
                   s=200, edgecolors='black', linewidth=2,
                   label=f'店铺{k + 1}' if idx == 0 else "")

    # 添加从每个点到其所属中心点的连线（只在分配步骤显示）
    if state['labels'] is not None and "分配顾客" in state['step']:
        # 每个簇只显示几个示例连线，避免过于拥挤
        for k in range(n_clusters):
            mask = state['labels'] == k
            if np.sum(mask) > 0:
                # 为每个簇选择3个点显示连线
                indices = np.where(mask)[0][:3]
                for i in indices:
                    point = X[i]
                    center = state['centers'][k]
                    ax.plot([point[0], center[0]], [point[1], center[1]],
                            color=cluster_colors[k % len(cluster_colors)],
                            alpha=0.4, linewidth=1, linestyle='--')

    # 如果是重新选址步骤，绘制中心点移动轨迹
    if "重新选址" in state['step'] and idx > 0:
        prev_state = history[idx - 1]
        for k in range(n_clusters):
            prev_center = prev_state['centers'][k]
            curr_center = state['centers'][k]
            ax.plot([prev_center[0], curr_center[0]],
                    [prev_center[1], curr_center[1]],
                    color=center_colors[k % len(center_colors)],
                    linewidth=2, alpha=0.6, linestyle='-')

    # 设置子图属性
    ax.set_xlim(-0.1, 1.1)
    ax.set_ylim(-0.1, 1.1)
    ax.set_xlabel('甜口喜好度', fontsize=10)
    ax.set_ylabel('咸口喜好度', fontsize=10)

    # 设置标题
    step_num = idx + 1
    title = f'第{step_num}步: {state["step"]}'
    ax.set_title(title, fontsize=12, fontweight='bold', color='darkblue')

    # 添加描述文本
    ax.text(0.5, -0.15, state['description'], transform=ax.transAxes,
            ha='center', fontsize=9, style='italic',
            bbox=dict(boxstyle='round', facecolor='lightyellow', alpha=0.7))

    ax.grid(True, alpha=0.2, linestyle='--')

    # 只在第一个子图添加完整图例
    if idx == 0:
        ax.legend(loc='upper right', fontsize=8)

# 隐藏多余的子图（如果有）
for idx in range(num_steps, len(axes)):
    axes[idx].axis('off')

# 调整布局
plt.suptitle('K-Means聚类过程：披萨店选址决策模拟',
             fontsize=16, fontweight='bold', y=1.02, color='darkred')
plt.tight_layout()

# 保存图片
plt.savefig('kmeans_process_corrected.png', dpi=150, bbox_inches='tight')
plt.show()

print("图片已保存为 'kmeans_process_corrected.png'")
print("\n步骤说明：")
print("1. 初始状态：展示散乱的数据点，用不同颜色区分潜在类别")
print("2. 随机选址：随机放置K个'店铺标志'（不同形状标记）")
print("3. 分配顾客：动画显示每个数据点奔向最近的店铺")
print("4. 重新选址：店铺移动到其顾客的中心位置")
print("5. 重新分配：由于店铺移动，有些顾客重新选择店铺")
print("6. 最终状态：展示2-3轮迭代后的结果")

print("\n教学提示：")
print("• 这个可视化展示了K-Means如何找到数据中的'热点中心'")
print("• 这对应RBFN的第一步：找到隐层神经元的中心点")
print("• 注意观察中心点如何逐步移动到每个簇的中心位置")
print("• 这个过程是无监督的，算法不知道数据的真实标签，仅根据位置相似性聚类")

展示K-Means聚类的6个关键步骤：

  1. 初始状态：散乱的数据点，用不同颜色区分潜在类别

  2. 随机选址：随机放置3个"店铺标志"（不同形状的黑色标记）

  3. 分配顾客：每个数据点"奔向"最近的店铺（显示虚线连线）

  4. 重新选址：店铺移动到其顾客的中心位置（显示移动轨迹）

  5. 重新分配：由于店铺移动，有些顾客重新选择店铺

  6. 再次重新选址：继续优化店铺位置

  • 注意：K-Means不需要知道顾客喜欢什么口味（无监督），仅根据位置分布就能找到热点

  • K值怎么选？就像决定开几家分店：需要经验或一些技术方法（如肘部法则），今天我们先假设K已知

  • 这些最终的中心点，就是我们RBFN的黄金店址！

如果让你在校园周边开奶茶店，你会把店址选在哪？------食堂门口、教学楼之间、宿舍区中心......这就是找中心！

法宝二：量距离------顾客离店有多远？

（1）找到店址后，问题变简单了：如何衡量任意位置到每个店的距离？

（2）如果顾客有更多特征呢？比如加上辣口度、酸口度？

这就是三维、四维空间中的距离，公式形式不变！

（3）在二维图上画出一个点到两个中心的距离线段

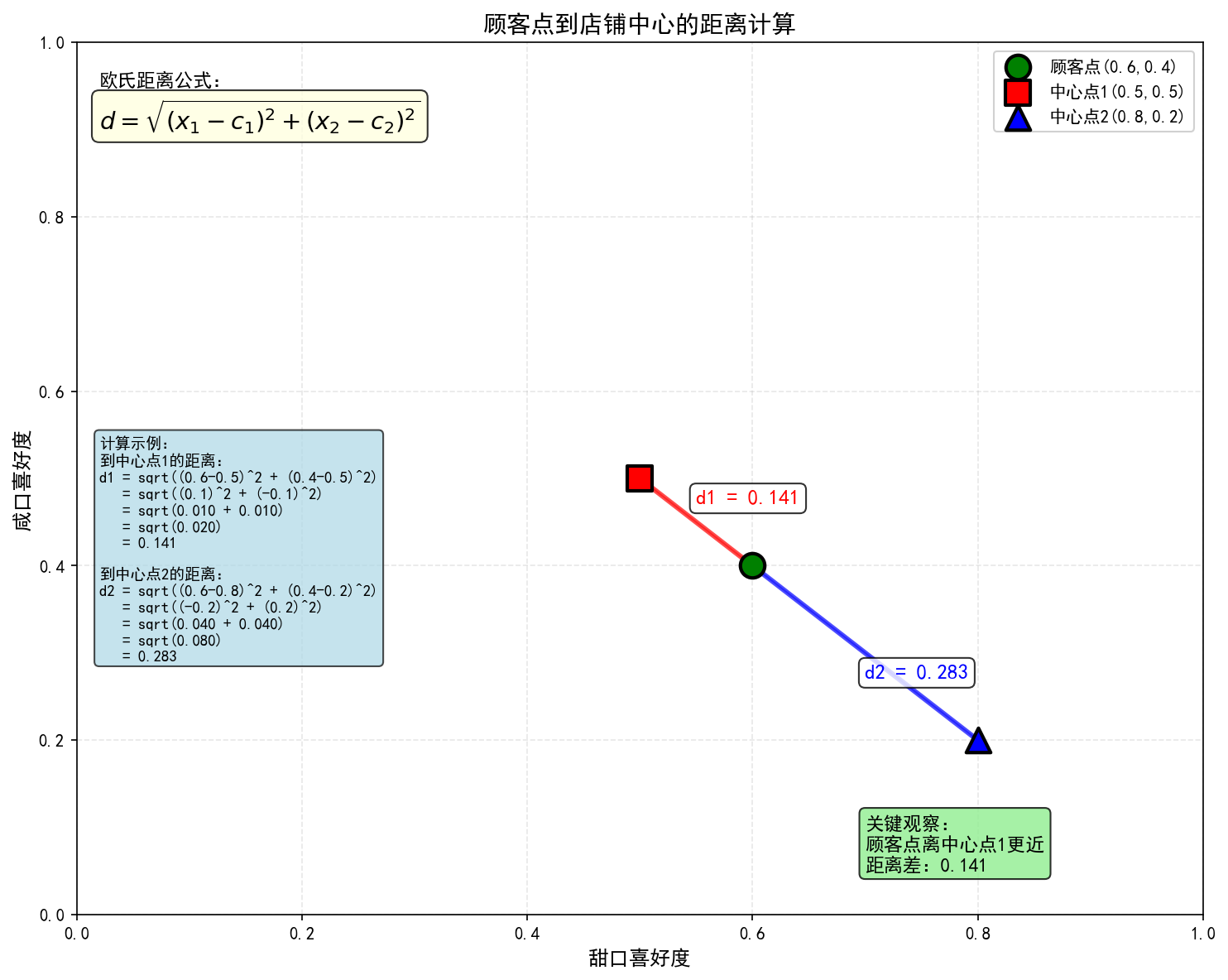
强调：距离永远是非负数，且对称的（A到B的距离 = B到A的距离）

【小测试】

给出一个点(0.6, 0.4)和两个中心(0.5,0.5)、(0.8,0.2)，大家可以心算一下哪个更近。

法宝三：算影响------本店能吸引这位顾客吗？

【从距离到影响力】

但距离本身还不够------5公里对便利店是天文距离，对大型购物中心却是可接受的。

我们需要把距离转化为影响力分数。

【引入高斯函数------美丽的钟形曲线】

展示标准正态分布曲线：

  1. 形状特征：对称、中间高两边低、平滑衰减

  2. 数学公式 ：

  3. 关键性质：

    • 当d=0（就在店里），影响力=1（最大值）

    • 当d增大，影响力快速下降

    • 永远为正，但趋近于0

【参数σ------控制影响力的'心胸'】
动态演示：滑动条控制σ值，观察曲线变化

  • σ=0.1（"精品小店"模式）：

    • 曲线又高又瘦

    • "只服务门口顾客，多走两步都不行"

    • 影响范围极小

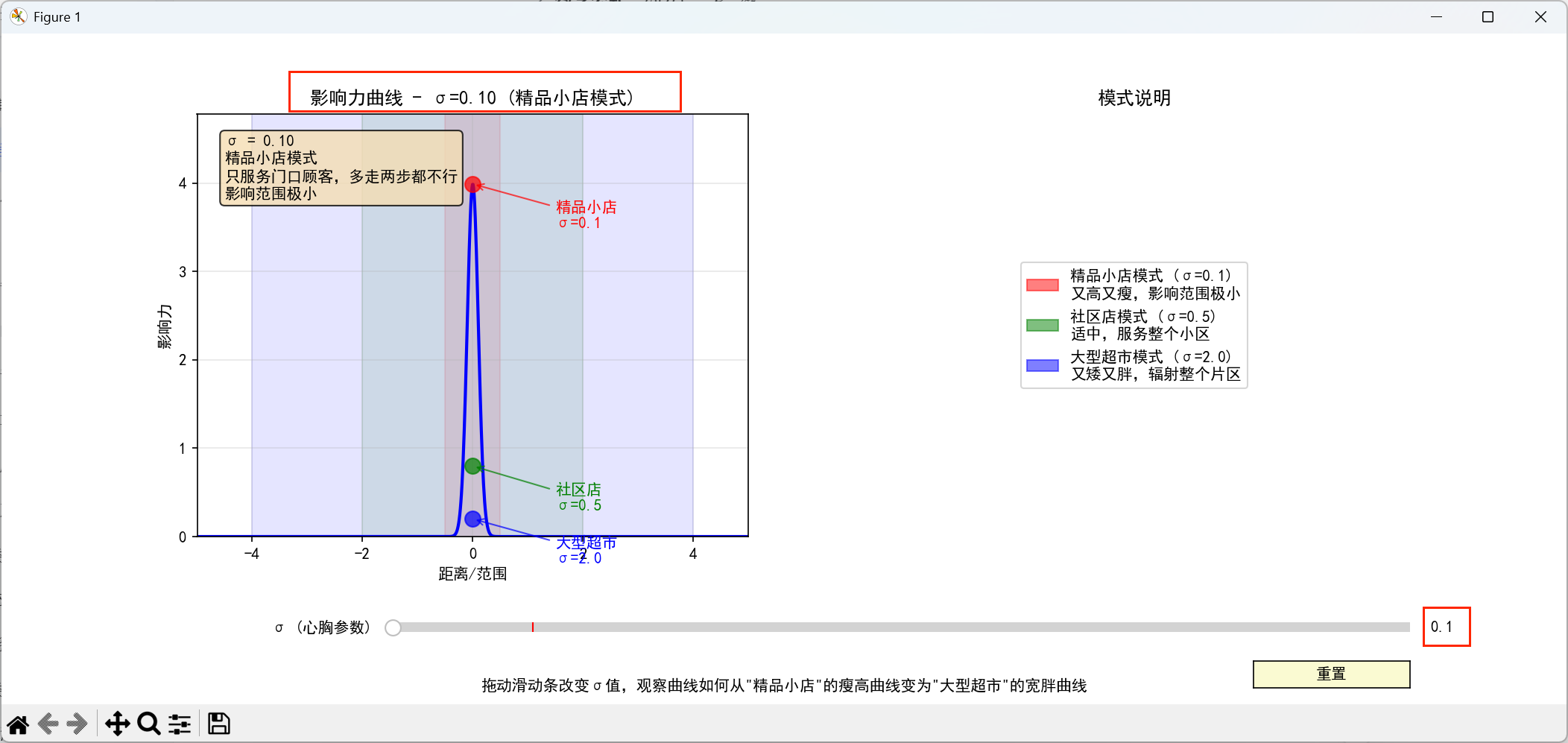
  • σ=0.5（"社区店"模式）：

    • 曲线适中

    • "服务整个小区，但不过界"

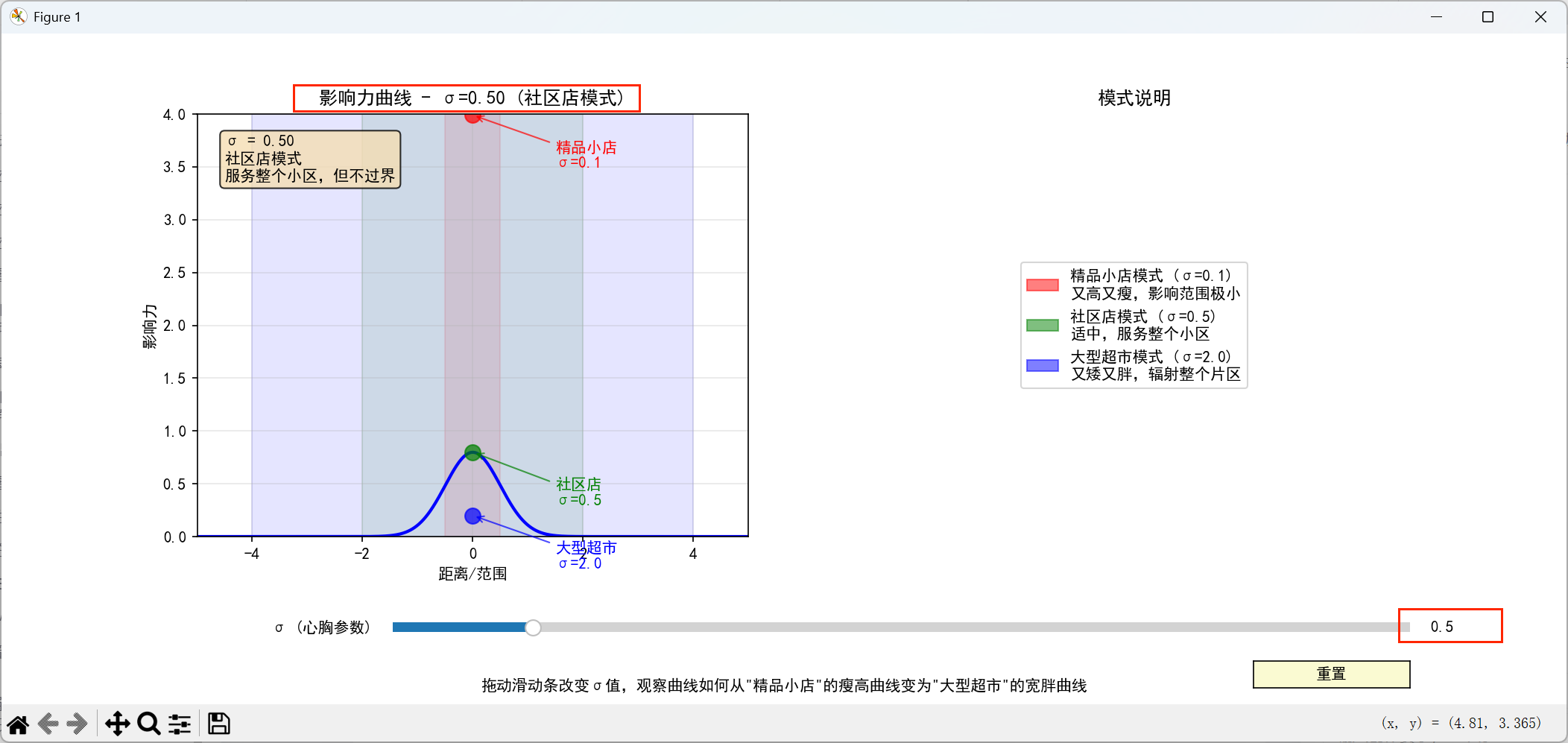
  • σ=2.0（"大型超市"模式）：

    • 曲线又矮又胖

    • "辐射整个片区，来者不拒"

    • 影响范围广但峰值不高

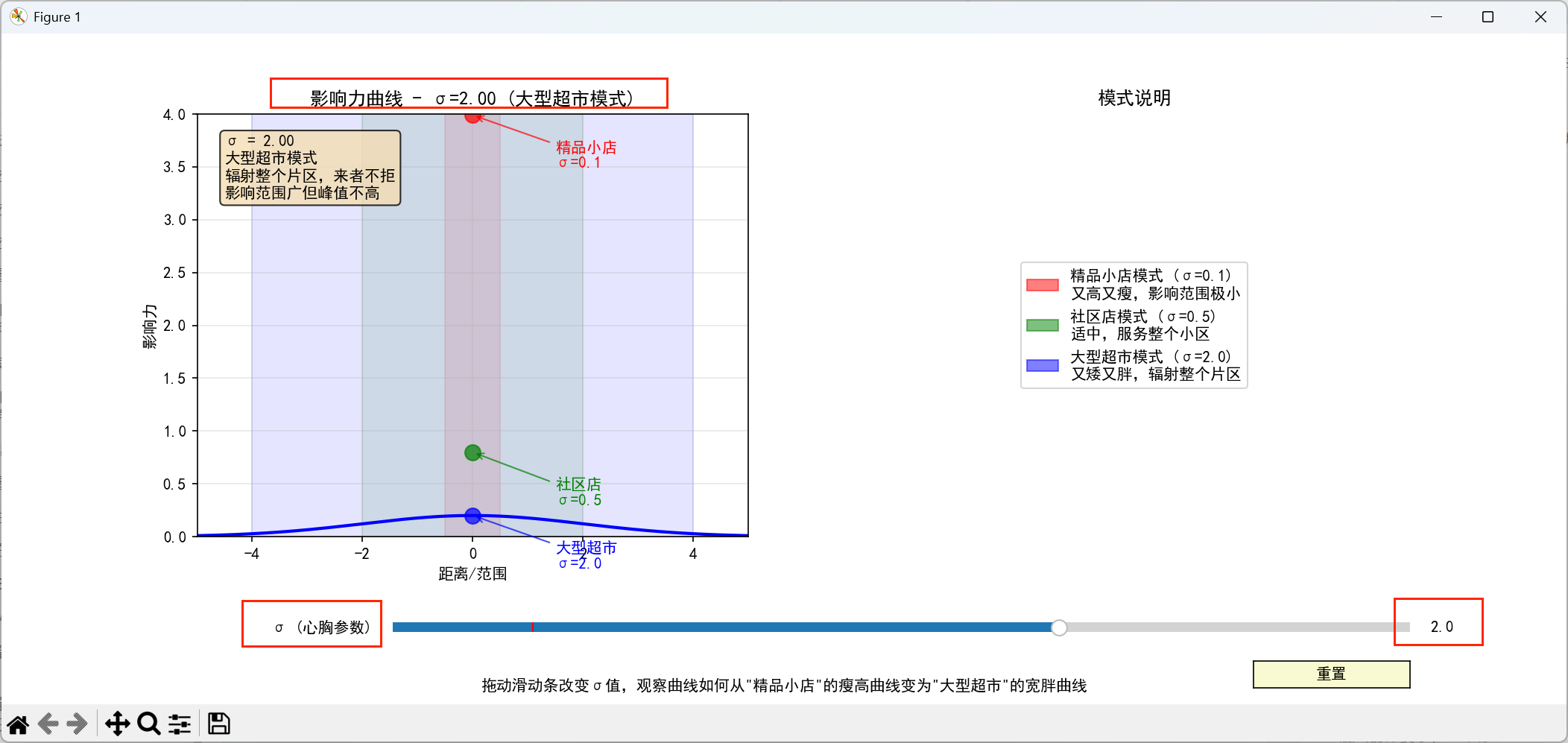
关于这个滑动条控制σ值的程序，我放在下面了，大家有兴趣可以试试：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider
import matplotlib.patches as mpatches

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 创建图形和轴
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
plt.subplots_adjust(bottom=0.25)

# 定义x轴范围
x = np.linspace(-5, 5, 1000)

# 初始化σ值
sigma_init = 0.5


# 高斯函数（正态分布）
def gaussian(x, sigma):
    return np.exp(-x ** 2 / (2 * sigma ** 2)) / (sigma * np.sqrt(2 * np.pi))


# 计算初始曲线
y_init = gaussian(x, sigma_init)

# 绘制初始曲线
line, = ax1.plot(x, y_init, 'b-', linewidth=2, label=f'σ={sigma_init}')
ax1.set_xlabel('距离/范围')
ax1.set_ylabel('影响力')
ax1.set_title('影响力曲线 - 不同σ值的影响')
ax1.grid(True, alpha=0.3)
ax1.set_xlim([-5, 5])
ax1.set_ylim([0, 4])

# 添加说明文本框
text_box = ax1.text(0.05, 0.95, '', transform=ax1.transAxes,
                    verticalalignment='top', bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.8))


# 更新说明文本
def update_text(sigma):
    if sigma <= 0.2:
        mode = "精品小店模式"
        desc = "只服务门口顾客，多走两步都不行\n影响范围极小"
    elif sigma <= 1.0:
        mode = "社区店模式"
        desc = "服务整个小区，但不过界"
    else:
        mode = "大型超市模式"
        desc = "辐射整个片区，来者不拒\n影响范围广但峰值不高"

    text_box.set_text(f'σ = {sigma:.2f}\n{mode}\n{desc}')
    return mode


# 初始化文本
initial_mode = update_text(sigma_init)

# 在右侧子图中添加示例模式
ax2.axis('off')
ax2.set_title('模式说明')

# 创建图例项
legend_elements = [
    mpatches.Patch(color='red', alpha=0.5, label='精品小店模式 (σ=0.1)\n又高又瘦，影响范围极小'),
    mpatches.Patch(color='green', alpha=0.5, label='社区店模式 (σ=0.5)\n适中，服务整个小区'),
    mpatches.Patch(color='blue', alpha=0.5, label='大型超市模式 (σ=2.0)\n又矮又胖，辐射整个片区')
]

# 添加图例
ax2.legend(handles=legend_elements, loc='center', fontsize=10, framealpha=0.8)

# 添加垂直区域表示不同模式
ax1.axvspan(-0.5, 0.5, alpha=0.1, color='red', label='精品小店范围')
ax1.axvspan(-2, 2, alpha=0.1, color='green', label='社区店范围')
ax1.axvspan(-4, 4, alpha=0.1, color='blue', label='大型超市范围')

# 添加滑动条轴
ax_sigma = plt.axes([0.25, 0.1, 0.65, 0.03], facecolor='lightgoldenrodyellow')

# 创建滑动条
sigma_slider = Slider(
    ax=ax_sigma,
    label='σ (心胸参数)',
    valmin=0.1,
    valmax=3.0,
    valinit=sigma_init,
    valstep=0.05
)

# 添加标记点表示特定模式
mode_sigmas = [0.1, 0.5, 2.0]
mode_labels = ['精品小店', '社区店', '大型超市']
mode_colors = ['red', 'green', 'blue']

# 绘制标记点
for i, (s, label, color) in enumerate(zip(mode_sigmas, mode_labels, mode_colors)):
    y_val = gaussian(0, s)  # 在x=0处的值
    ax1.plot(0, y_val, 'o', color=color, markersize=10, alpha=0.7)
    ax1.annotate(f'{label}\nσ={s}', xy=(0, y_val), xytext=(1.5, y_val - 0.5),
                 arrowprops=dict(arrowstyle="->", color=color, alpha=0.7),
                 color=color, fontweight='bold')


# 更新函数，当滑动条值改变时调用
def update(val):
    sigma = sigma_slider.val
    y = gaussian(x, sigma)
    line.set_ydata(y)

    # 更新y轴范围以更好地显示曲线
    max_y = max(y) * 1.2
    ax1.set_ylim([0, max(4, max_y)])

    # 更新文本
    update_text(sigma)

    # 更新标题
    mode = update_text(sigma)
    ax1.set_title(f'影响力曲线 - σ={sigma:.2f} ({mode})')

    fig.canvas.draw_idle()


# 注册更新函数
sigma_slider.on_changed(update)


# 添加重置按钮功能
def reset(event):
    sigma_slider.reset()


# 添加重置按钮轴
resetax = plt.axes([0.8, 0.025, 0.1, 0.04])
button = plt.Button(resetax, '重置', color='lightgoldenrodyellow', hovercolor='0.975')

# 连接重置按钮
button.on_clicked(reset)

# 添加动态效果说明
fig.text(0.5, 0.02,
         '拖动滑动条改变σ值，观察曲线如何从"精品小店"的瘦高曲线变为"大型超市"的宽胖曲线',
         ha='center', fontsize=10, style='italic')

plt.show()

这个程序创建了一个交互式可视化，具有以下特点：

  1. 左侧图表：

    • 显示高斯函数曲线，表示影响力随距离衰减

    • 不同σ值产生不同形状的曲线

    • 彩色区域表示不同模式的影响范围

  2. 右侧说明：

    • 展示三种典型模式的说明

    • 使用图例清晰说明每种模式的特点

  3. 交互功能：

    • 滑动条控制σ值从0.1到3.0

    • 动态更新曲线形状和说明文本

    • 重置按钮恢复初始状态

  4. 三种典型模式标记：

    • σ=0.1（红色）："精品小店"模式 - 曲线瘦高，影响范围小

    • σ=0.5（绿色）："社区店"模式 - 曲线适中

    • σ=2.0（蓝色）："大型超市"模式 - 曲线宽胖，影响范围广

【可视化成影响力小山包】

  1. 在二维平面上展示一个中心点

  2. 生成三维曲面：z = φ(d(x,y))

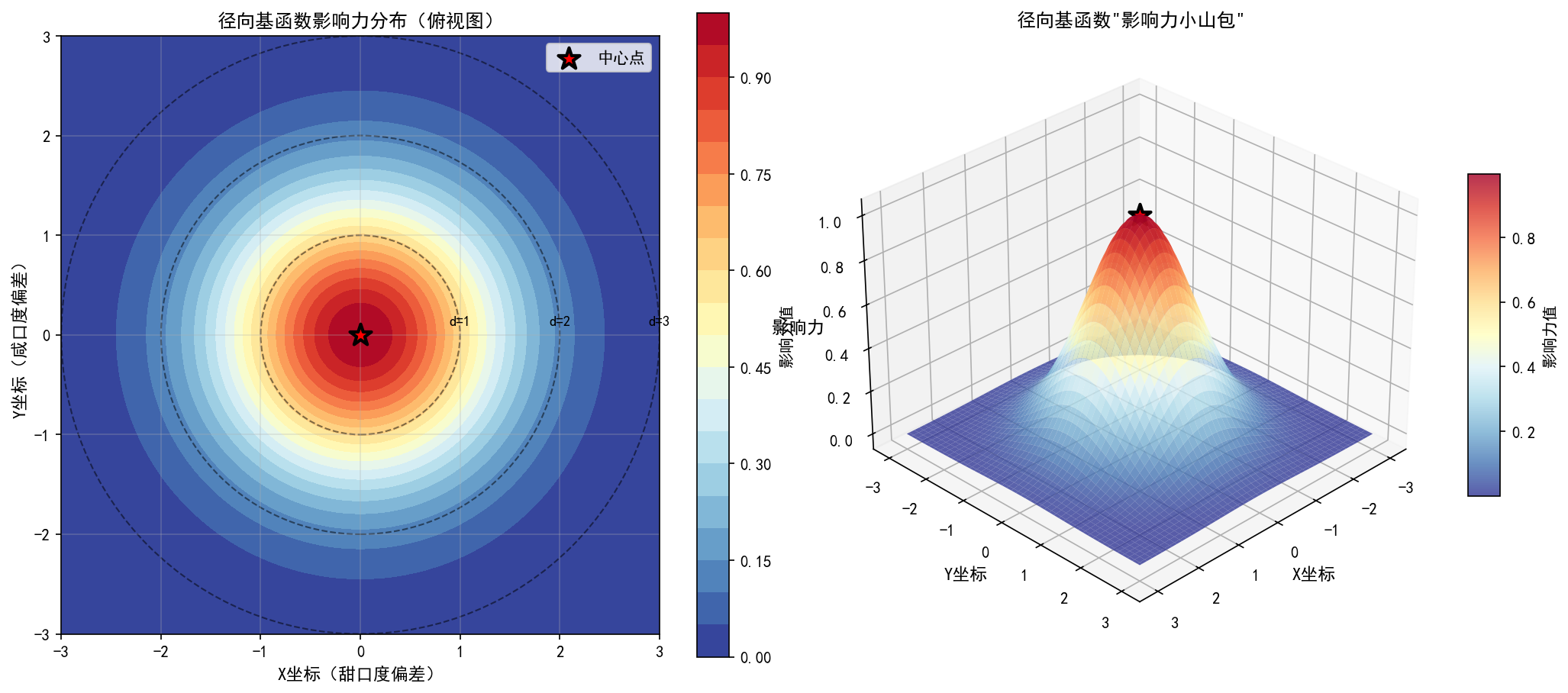
  1. 观察：以中心为山顶，向四周平滑下降的小山

  2. 展示多个中心点的多个小山包并列

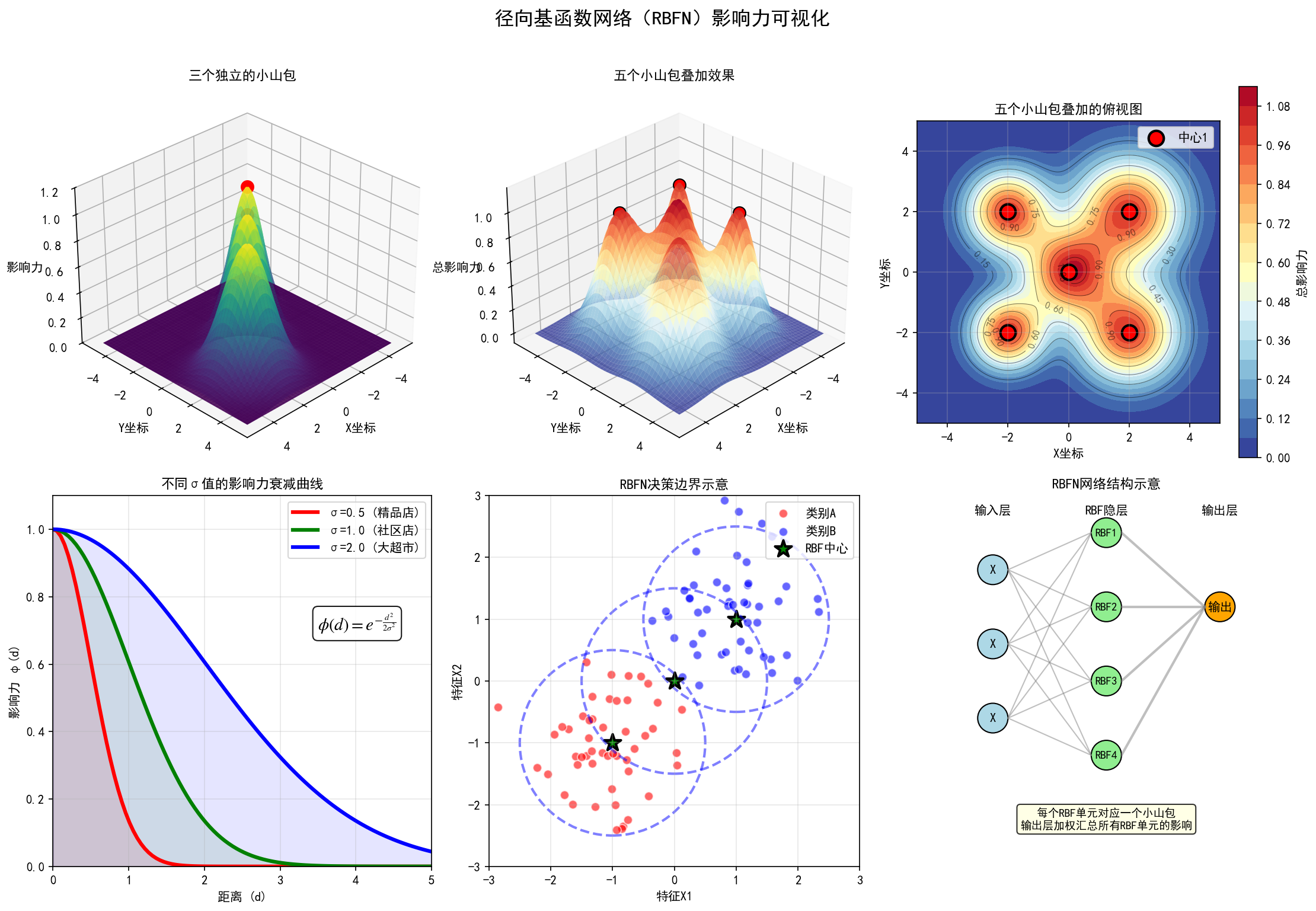
【串联三法宝】

现在，对于一个新顾客的位置：

  1. 量距离：计算他到每个中心的距离d₁, d₂, ..., dₖ

  2. 算影响：通过高斯函数得到影响力分数φ₁, φ₂, ..., φₖ

  3. 这些φ值就是隐层神经元的输出------每个分店对这个顾客的吸引力报告

第三部分：网络运作与对比------总部如何做决策？

完整网络流程图

【结构总览】

绘制清晰的RBFN结构图：

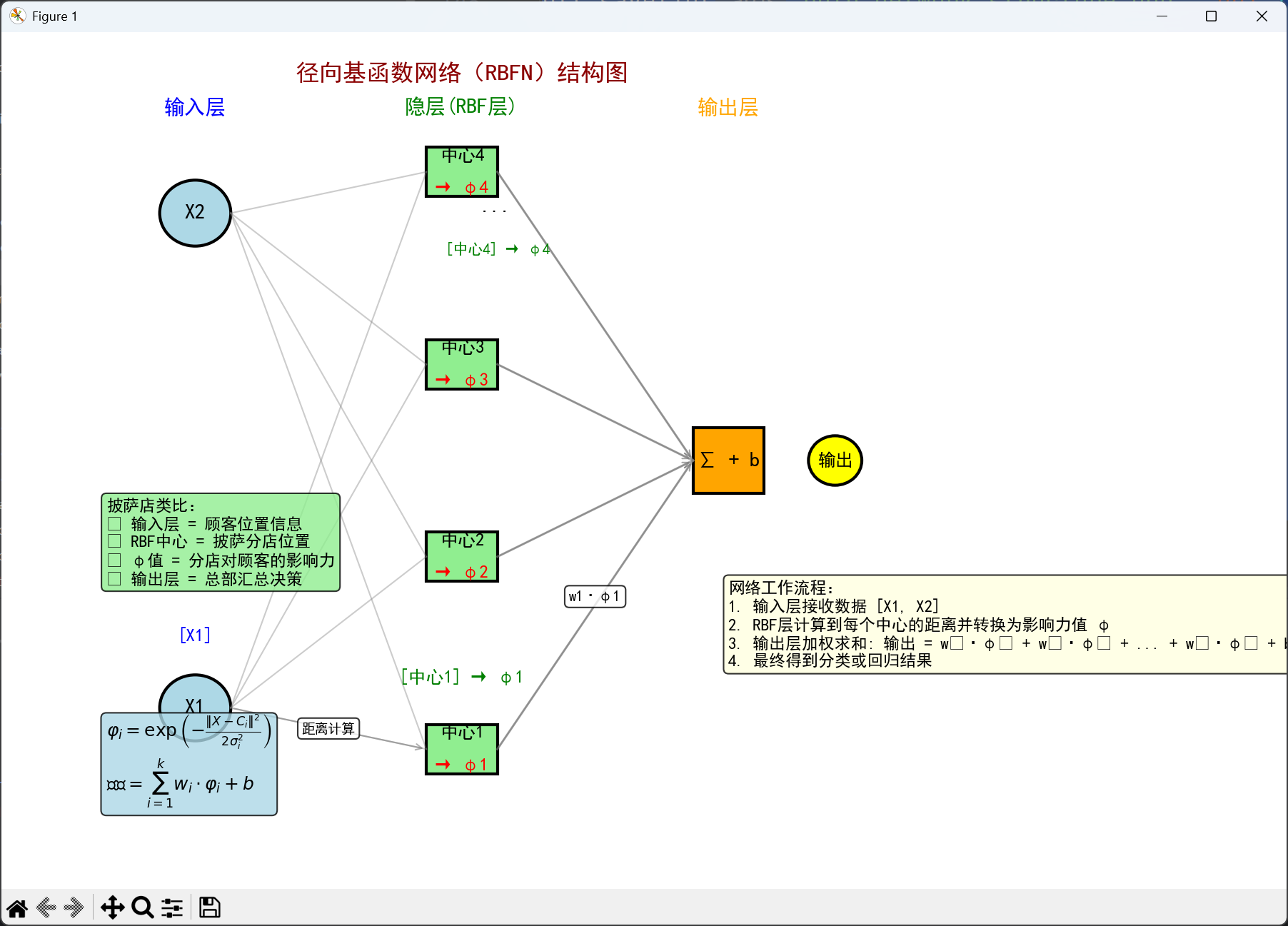
【分步解说案例】
案例： 顾客A的甜口度=0.8，咸口度=0.3 → 输入向量 [0.8, 0.3]

步骤1：输入传递

"顾客位置信息送达网络"

步骤2：隐层计算（各分店独立评估）

中心点1 (0.5, 0.5)

距离：

影响力：

中心点2 (0.7, 0.2)

距离：

影响力：

步骤3：输出层汇总（总部决策）

"总部收到各分店的报告：[φ₁=0.24, φ₂=0.96, φ₃=0.05, ...]"

"但总部知道：有的分店经验丰富（权重w大），有的刚开业（w小）"

加权求和：

输出 = w₁·φ₁ + w₂·φ₂ + ... + wₖ·φₖ + b

【权重与偏置的直观解释】

  • 权重w："话语权系数"

    • w为正：该分店推荐"是"，会增加最终输出

    • w为负：该分店推荐"否"，会减少最终输出

    • |w|大：该分店意见很重要

  • 偏置b："基础倾向"

    • 好比"在没有分店意见时，总部的默认决策"

    • b>0：默认倾向"是"

    • b<0：默认倾向"否"

相关推荐
熊文豪2 小时前
借助 AI Ping 的 Kimi-K2-Thinking 与 ClaudeCode 的加解密工具开发
人工智能·aiping
阿杰学AI2 小时前
AI核心知识45——大语言模型之PPO（简洁且通俗易懂版）
人工智能·ai·语言模型·自然语言处理·aigc·ppo·近端策略优化
da_vinci_x2 小时前
PS 神经滤镜：一张夏天变雪景？场景美术的“季节魔术”
人工智能·3d·aigc·建模·游戏美术·pbr·场景美术
深蓝易网2 小时前
MES系统如何帮助企业实现产品质量的全过程追溯
大数据·人工智能
free-elcmacom2 小时前
机器学习进阶＜7＞人脸识别特征锚点Python实现
人工智能·python·机器学习·rbfn
天才少女爱迪生2 小时前
图像序列预测有什么算法方案
人工智能·python·深度学习·算法
计算机学姐2 小时前
基于Python的高校后勤报修系统【2026最新】
开发语言·vue.js·后端·python·mysql·django·flask
乐迪信息2 小时前
乐迪信息：AI摄像机+反光衣佩戴检测，保障智慧煤矿人员作业安全
大数据·运维·人工智能·物联网·安全
胖墩会武术2 小时前
【PyTorch项目实战】Ultralytics YOLO模型本地部署（训练 + 测试 + 推理）
人工智能·pytorch·yolo
热门推荐
01GitHub 镜像站点02【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）03UV安装并设置国内源04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05React CVE-2025-55182漏洞排查与修复指南06Linux下V2Ray安装配置指南07BongoCat - 跨平台键盘猫动画工具08解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10从入门到实战：Gemini 3 使用指南速览