【强化学习】第二章：老虎机问题、ε-greedy算法、指数移动平均

【强化学习】第二章：老虎机问题、ε-greedy算法、指数移动平均

一、从老虎机问题->强化学习算法

1、老虎机问题 上图是一组多台老虎机 ，每台老虎机的特点 都各不相同 ，就是有的机器赢得多，有的机器输得多。但是每台老虎机的特点 是固定的 ，就是每台机器的奖励的概率是固定的：

上图是机器a和机器b的奖励的概率分布表。所以理论上，对于每台机器，只要你玩的次数足够多，比如无限次，根据大数定律，那你得到的硬币的平均数量 就是一个固定的 期望值(expectation value):

老虎机a：0 x 0.70 + 1 x 0.15 + 5 x 0.12 + 10 x 0.03 = 1.05

老虎机b：0 x 0.50 + 1 x 0.40 + 5 x 0.09+ 10 x 0.01 =0.95

如果我们把这个期望值当作选哪台老虎机来玩的指标，显然我们都会选择a机器玩。因为a比b赢得更多。所以不管我们能玩几次，1次或者10次，我们会次次都选机器a来玩。也就是选择机器a就是我们最好的策略。

但是现在的问题，玩家在玩老虎机时往往是不知道 每台机器的特点 的，也就是不知道 每台机器的奖励期望值 ，所以玩家需要尽可能准确的去估计每台老虎机的期望值 ，然后根据评估结果去选择一台机器玩。所以问题就转化为：玩家如何找到具有最大奖励期望值的老虎机？ 那自然是需要玩家切切实实的玩过一组机器，然后根据结果寻找看起来还不错的机器。用数学语言就是从每次玩老虎机获得的硬币的平均值，作为玩这台老虎机的期望 奖励的估计值 ：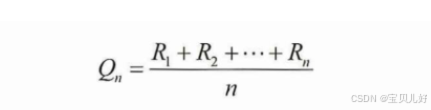

上面公式中的n表示，对于某台 老虎机，玩家实际中实实在在玩的次数。每次玩一局，就会有一个R奖励。玩了n次，那就是这n次的平均奖励 。我们就把这个平均奖励就当成这台老虎机的期望奖励。

我们实际地玩老虎机获得的奖励是基于某个概率分布产生的"样本"(sample)。因此，实际获得的奖励的平均值可以称为样本均值。随着采样次数的增加，样本均值就会越来越接近真实值(也就是奖励的期望值)。根据"大数定律"，如果采样的次数无限多，那么样本均值将与真实值相等。

2、强化学习框架

上图就是强化学习的框架，你可以把智能代理 理解为agent，奖励和状态理解为环境 。agent被置于环境中，通过观察环境中的状态 ，并在此状态下做出行动 ，行动导致agent所处的环境的状态发生改变，同时得到环境的奖励。如此反复，agent观察新状态->采取动作->获得奖励的同时进入下一个新环境.....

3、从老虎机问题到强化学习的基本特征 ：

（1）一组老虎机 可以类比到强化学习中的环境 (environment)概念。

（2）玩老虎机的人就是强化学习中的智能体 (agent)，并且agent是在强化学习的框架内和环境进行互动 。

（3）玩家从多台老虎机中选择一台来玩，在强化学习中就是agent采取的行动 (action)。

（4）玩家玩完的结果，也就是从老虎机中获得的硬币，就是强化学习中的奖励(reward)。

4、从强化学习算法角度设计老虎机问题

要实现上面老虎机问题，我们至少得写下面两个类：

（1）要写一个环境类 。这个类要实现：一是，初始化一组有固定胜率 的老虎机。二是，当agent选择了其中某台老虎机，并打完游戏，要返回agent一个奖励。为了让问题更加简单清晰，我们只考虑老虎机返回的硬币数量为0或1的情况。就是假设在玩老虎机时，得到的奖励要么是1（就是赢了的意思）,要么是0（就是输了的意思）。假如某台老虎机的胜率是0.4，就是如果你选择了这台老虎机来玩，那你有40%的机会赢得游戏得1枚硬币，有60%的机会输了游戏得0枚硬币。

（2）需要再写一个agent类 。这个类是要实现：智能体可以对以往的游戏结果进行记录。为了让过程简单，一是，我们假设智能体每次玩游戏的结果都是随机的 。二是，先假设智能体每次都是随机选择一台老虎机开始玩游戏的。

下面用代码实现上面两个类：

# agent0每次玩游戏都是随机选择老虎机来玩，每局游戏的结果也是随机的
class Env:
    def __init__(self, set_of_tiger):
        np.random.seed(0)
        self.machine_winning_rate = np.random.rand(set_of_tiger)    #[0, 1)区间内的均匀分布的随机数
    def reward(self, tiger_index, play_result):
        if play_result < self.machine_winning_rate[tiger_index]: 
            return 1     #如果agent打游戏的结果<那台机器的胜率，就得1分奖励
        else:
            return 0    #否则，表示打输了游戏，得0分奖励。
        
class Agent0:
    def __init__(self, action_times, set_of_tiger):        #记录智能体打游戏的结果
        self.ns = np.zeros(set_of_tiger)         #记录每次游戏都是选择的哪台老虎机
        self.Qs = np.zeros(set_of_tiger)        #初始化每台老虎机的胜率都是0
        
    def choose_machine(self, set_of_tiger):
        tiger_index = np.random.randint(0, set_of_tiger)  #假设智能体每次玩游戏都是随机选择一台老虎机来玩的
        return tiger_index
    
    def play(self):
        play_result = np.random.rand()   #假设agent的打游戏的结果也是随机的。
        return play_result
        
    def record(self, tiger_index, reward):
        self.ns[tiger_index] += 1
        self.Qs[tiger_index] += reward

#假如有5台老虎机，agent总共玩了2500次游戏
set_of_tiger=5
num_games = 2500
env = Env(set_of_tiger=set_of_tiger)
agent0 = Agent0(action_times=num_games, set_of_tiger=set_of_tiger)
print("每台老虎机设置的胜率是：", env.machine_winning_rate)

for i in range(num_games):    #agent开始玩这2500次游戏
    tiger_index = agent0.choose_machine(set_of_tiger)   #随机选择一台老虎机玩
    play_re = agent0.play()   #玩的结果
    reward_i = env.reward(tiger_index, play_re)  #获得的奖励
    agent0.record(tiger_index, reward_i)   #记录玩的结果

print("每台老虎机玩的次数：",  agent0.ns)
print("玩老虎机获得的奖励：", agent0.Qs)
print("统计每台老虎机的胜率：",  agent0.Qs/agent0.ns)
print("agent0玩2500次游戏，共得到的奖励：", sum(agent0.Qs))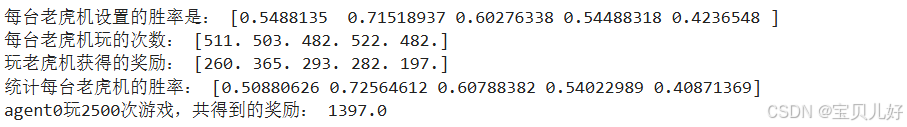

上面环境中的一组老虎机 ，我设置的是5台。每台老虎机的胜率是随机生成的，是0到1之间均匀分布的随机数。
智能体agent0 每次玩游戏是随机选择一台老虎机来玩的。agent0每次玩游戏的结果也是随机的。

当agent0玩游戏的结果(随机数)< 那台老虎机的胜率时，我们就认为agent0本局游戏获胜，得到1分的奖励。否则就是玩输了，0分奖励。

可见，只要agent0打过足够多次游戏，它就能根据过往的行为，比较准确的预测到每台老虎机的胜率。从上面的结果看，差不多每台老虎机玩500次左右，统计结果就基本接近真实结果了。

二、老虎机算法优化1：用增量计算平均奖励

上述代码我们需要保存每台老虎机被玩的次数 和每台老虎机的奖励 两个数组，才能计算老虎机的期望奖励。在现实中，随着游戏次数n的增加，内存占用和计算量都会增加。而我们要算期望奖励的目的是找到胜率最大的那台老虎机，并一直用这台老虎机玩游戏，最终获得最多的奖励。所以我们的目的不是记录奖励，而是计算期望奖励，所以后人在计算上进行了下面的优化：

上述就是增量式 实现期望奖励的计算过程。如此计算，我们就可以省去一个数组的内存，只保留一个标量即可。下面用代码展示这个优化过程：

#优化1：用增量计算平均奖励
class Env:
    def __init__(self, set_of_tiger):
        np.random.seed(0)
        self.machine_winning_rate = np.random.rand(set_of_tiger)
    def reward(self, tiger_index, play_result):
        if play_result < self.machine_winning_rate[tiger_index]: 
            return 1 
        else:
            return 0 
        
class Agent1:
    def __init__(self, action_times, set_of_tiger): 
        self.ns = np.zeros(set_of_tiger) 
        self.Qs = np.zeros(set_of_tiger)
        
    def choose_machine(self, set_of_tiger):
        tiger_index = np.random.randint(0, set_of_tiger)
        return tiger_index
    
    def play(self):
        play_result = np.random.rand()
        return play_result
        
    def record(self, tiger_index, reward):
        self.ns[tiger_index] += 1
        self.Qs[tiger_index] += (reward-self.Qs[tiger_index])/self.ns[tiger_index]   ###重点：用增量计算
        
#依然假设有5台老虎机，agent总共玩了2500次游戏        
set_of_tiger=5
num_games = 2500
env = Env(set_of_tiger=set_of_tiger)
agent1 = Agent1(action_times=num_games, set_of_tiger=set_of_tiger)
print("每台老虎机设置的出厂胜率是：", env.machine_winning_rate)

for i in range(num_games):
    tiger_index = agent1.choose_machine(set_of_tiger)   #随机选择一台老虎机玩
    play_re = agent1.play()   #玩的结果
    reward_i = env.reward(tiger_index, play_re)  #获得的奖励
    agent1.record(tiger_index, reward_i)   #记录玩的结果
    
print("每台老虎机玩的次数：",  agent1.ns)
print("统计每台老虎机的胜率：", agent1.Qs)
print("玩2500次游戏，agent1总共得到的奖励：", sum(agent1.ns * agent1.Qs))
print("每台老虎机得的奖励是：", agent1.ns * agent1.Qs)

可见，agent1和agent0实质上并无异的，只是计算方式不一样，所有的结果都是一样的。

三、老虎机算法优化2：ε-greedy算法

上面二的优化仅仅是工程方面的优化，这里我们开始算法上 的优化，就是让这个智能体更加智能，这里我们加上玩家的策略 。agent0和agent1每次玩游戏都是随机选择老虎机来玩的。但是我们的目标 是在给定的游戏次数内、获得尽可能多的硬币 。所以我们还是得选择期望奖励最高的老虎机来玩 ，或者说得找到具有最大期望奖励的老虎机来玩 ，也就是根据到目前为止的实际游戏结果(之前的经验)，选择最好的老虎机 。这就是智能体的策略。

具体来说，玩家可以考虑选择估计值(实际获得的奖励的平均值)最大的老虎机。这种做法可以称为"贪婪行动"(greedy)，意味着"只从手头的信息中选择最好的方法，而不考虑将来"。 但是贪婪行动也存在问题，因为估计值存在"不确定性"，我们不可能仅仅根据玩几次的结果就估计出哪个老虎机好从而一直玩那一台老虎机，而是要不断尝试，减少不确定性，增强估计值的可靠性，玩家可以尝试以下两种做法：

利用目前实际的游戏结果，玩那些看起来最好的老虎机(贪婪行动)。

为了对老虎机的价值做出更准确的估计，尝试不同的老虎机。

上述第一种做法是根据以前的经验选择最佳行动。这就是"贪婪行动"，在强化学习中叫作利用 (exploitation)。如果玩家采取贪婪行动的做法，那么玩家将根据以前的经验选择最佳行动。但这样做也有可能错过更好的选择。因此，玩家需要尝试第二种做法："非贪婪行动"，这种做法在强化学习中叫作探索(exploration)。通过探索，玩家可以对每台老虎机的价值做出更准确的估计。

在老虎机问题中，如果想在下一次尝试中得到一个好的结果，那么玩家就应该采取"利用"的做法。但从长期来看，如果想获得好的结果，那么玩家需要的是"探索"。这是因为通过"探索"，玩家找到更好的老虎机的概率更大。如果能找到更好的机器，那么此后就可以一直选择该机器，长期来看会获得更好的结果。

强化学习算法最终归结为如何在"利用"和"探索"之间取得平衡 。为了取得这种平衡，人们提出了各种算法，这些算法既有简单的，也有复杂的，其中最基本、最常用的是ε-greedy算法，以ε的概率(比如ε=10%)进行"探索"，以1-ε的概率进行"利用"的方法。"探索"过程会随机地选择行动，也就是尝试不同的行动，使得对每台老虎机胜率的估计变得更加可靠，然后再以1-ε的概率执行贪婪行动(利用)。下面是智能体采用ε-greedy策略的实现代码：

#agent选择老虎机时采取贪婪策略:epsilon=0.1
class Env:
    def __init__(self, set_of_tiger):
        np.random.seed(0)
        self.machine_winning_rate = np.random.rand(set_of_tiger)
    def reward(self, tiger_index, play_result):
        if play_result < self.machine_winning_rate[tiger_index]: 
            return 1 
        else:
            return 0 
        
class Agent2:
    def __init__(self, action_times, set_of_tiger, epsilon): 
        self.ns = np.zeros(set_of_tiger) 
        self.Qs = np.zeros(set_of_tiger)
        self.epsilon = epsilon
        
    def choose_machine(self, set_of_tiger):   ###重点：这里就是ε-greedy策略
        if np.random.rand() < self.epsilon:  #当概率小于0.1我就"探索"
            tiger_index = np.random.randint(0, set_of_tiger)
        else:      #当概率大于0.1我就"利用"
            tiger_index = np.argmax(self.Qs)#就是在以往的经验中选择期望奖励最大的机器玩
        return tiger_index
    
    def play(self):
        play_result = np.random.rand()
        return play_result
        
    def record(self, tiger_index, reward):
        self.ns[tiger_index] += 1
        self.Qs[tiger_index] += (reward-self.Qs[tiger_index])/self.ns[tiger_index]
        
#依然假设有5台老虎机，agent总共玩了2500次游戏                
set_of_tiger=5
num_games = 2500
epsilon = 0.1
env = Env(set_of_tiger=set_of_tiger)
agent2 = Agent2(action_times=num_games, set_of_tiger=set_of_tiger, epsilon=epsilon)
print("每台老虎机设置的出厂胜率：", env.machine_winning_rate)

for i in range(num_games):   #使用ε-greedy策略，玩这2500次游戏
    tiger_index = agent2.choose_machine(set_of_tiger) 
    play_re = agent2.play()   #玩的结果
    reward_i = env.reward(tiger_index, play_re)  #获得的奖励
    agent2.record(tiger_index, reward_i)   #记录玩的结果
    
print("每台老虎机玩的次数：",  agent2.ns)
print("统计每台老虎机的胜率：", agent2.Qs)
print("agent2打2500轮游戏的奖励总和：", sum(agent2.ns * agent2.Qs))
print("每台老虎机得的奖励是：", agent2.ns * agent2.Qs)

可见，我们给智能体添加上策略后，同样是2500次游戏，随机选择机器玩是1397分的奖励，使用了ε-greedy策略后的奖励是1748分的奖励！

从结果上看，虽然agent2对每台老虎机的胜率的评估没有agent1准确，但是得分却比agent1多，我们的目标就是得最多的奖励。事实上，评估每台老虎机的胜率本身也是为了获取对多的奖励。

从实验中我们还可以看到："利用和探索"之间的平衡是通过ε值来调整的。下面我们再看看其他ε的结果：

#贪婪策略:epsilon=0.12
class Env:
    def __init__(self, set_of_tiger):
        np.random.seed(0)
        self.machine_winning_rate = np.random.rand(set_of_tiger)
    def reward(self, tiger_index, play_result):
        if play_result < self.machine_winning_rate[tiger_index]: 
            return 1 
        else:
            return 0 
        
class Agent3:
    def __init__(self, action_times, set_of_tiger, epsilon): 
        self.ns = np.zeros(set_of_tiger) 
        self.Qs = np.zeros(set_of_tiger) 
        self.epsilon = epsilon
        
    def choose_machine(self, set_of_tiger):
        if np.random.rand() < self.epsilon: 
            tiger_index = np.random.randint(0, set_of_tiger)
        else:
            tiger_index = np.argmax(self.Qs)
        return tiger_index
    
    def play(self):
        play_result = np.random.rand() 
        return play_result
        
    def record(self, tiger_index, reward):
        self.ns[tiger_index] += 1
        self.Qs[tiger_index] += (reward-self.Qs[tiger_index])/self.ns[tiger_index]
        
set_of_tiger=5
num_games = 2500
epsilon = 0.12
env = Env(set_of_tiger=set_of_tiger)
agent3 = Agent3(action_times=num_games, set_of_tiger=set_of_tiger, epsilon=epsilon)
print("每台老虎机设置的出厂胜率：", env.machine_winning_rate)

for i in range(num_games):
    tiger_index = agent3.choose_machine(set_of_tiger)   #随机选择一台老虎机玩
    play_re = agent3.play()   #玩的结果
    reward_i = env.reward(tiger_index, play_re)  #获得的奖励
    agent3.record(tiger_index, reward_i)   #记录玩的结果
    
print("每台老虎机玩的次数：",  agent3.ns)
print("统计每台老虎机的胜率：", agent3.Qs)
print("agent3打2500轮游戏的奖励总和：", sum(agent3.ns * agent3.Qs))
print("每台老虎机得的奖励是：", agent3.ns * agent3.Qs)

这个结果是1755分，比agent2的得分还高。这个epsilon=0.12是我用网格搜索找到的最好的超参数。当然我们也应该能看到这个游戏的得分上限，就是2500次游戏都用第二台机器打：

#假如一直用第二台老虎机玩游戏
class Env:
    def __init__(self, set_of_tiger):
        np.random.seed(0)
        self.machine_winning_rate = np.random.rand(set_of_tiger)
    def reward(self, tiger_index, play_result):
        if play_result < self.machine_winning_rate[tiger_index]: 
            return 1 
        else:
            return 0 
        
class Agent4:
    def __init__(self, action_times, set_of_tiger): 
        self.ns = np.zeros(set_of_tiger) 
        self.Qs = np.zeros(set_of_tiger)
        
    def choose_machine(self, set_of_tiger):   #永远选择第二台机器玩
        return 1
    
    def play(self):
        play_result = np.random.rand() 
        return play_result
        
    def record(self, tiger_index, reward):
        self.ns[tiger_index] += 1
        self.Qs[tiger_index] += (reward-self.Qs[tiger_index])/self.ns[tiger_index]
        
set_of_tiger=5
num_games = 2500
env = Env(set_of_tiger=set_of_tiger)
agent4 = Agent4(action_times=num_games, set_of_tiger=set_of_tiger)
print("每台老虎机的胜率：", env.machine_winning_rate)

for i in range(num_games):
    tiger_index = agent4.choose_machine(set_of_tiger)   #随机选择一台老虎机玩
    play_re = agent4.play()   #玩的结果
    reward_i = env.reward(tiger_index, play_re)  #获得的奖励
    agent4.record(tiger_index, reward_i)   #记录玩的结果
    
agent4.ns
agent4.Qs
print("agent4打2500轮游戏的奖励总和：", sum(agent4.ns * agent4.Qs))

这是我们站在上帝视角，最终的得分。

小结：在老虎机问题以及强化学习中，在"利用和探索"之间取得平衡很重要。除了epsilon-greedy算法，人们还提出了解决老虎机问题的许多其他方法，典型的方法包括UCB (Upper Confidence Bound)算法和梯度老虎机算法。

四、非稳态的老虎机问题

上面我们把老虎机出厂设置的胜率都固定下来，这类问题是稳态问题 ，就是环境不发生变化，每次游戏的环境都是一成不变的。非稳态问题是每次游戏环境都会发生变化，就是每次游戏老虎机的胜率是不固定的，有时胜率高有时胜率低。这样的问题设置叫作非稳态问题。

对于非稳态问题，环境(老虎机)随时间变化，就是过去获得的奖励的重要性是应该随着时间的推移而下降的，也就是我们在计算期望奖励的时候，要给新获得的奖励更大的权重。

对于稳态问题 我们计算期望奖励用的是样本均值 ，那非稳态问题 我们就得用指数移动平均 (exponential moving average)来计算期望奖励：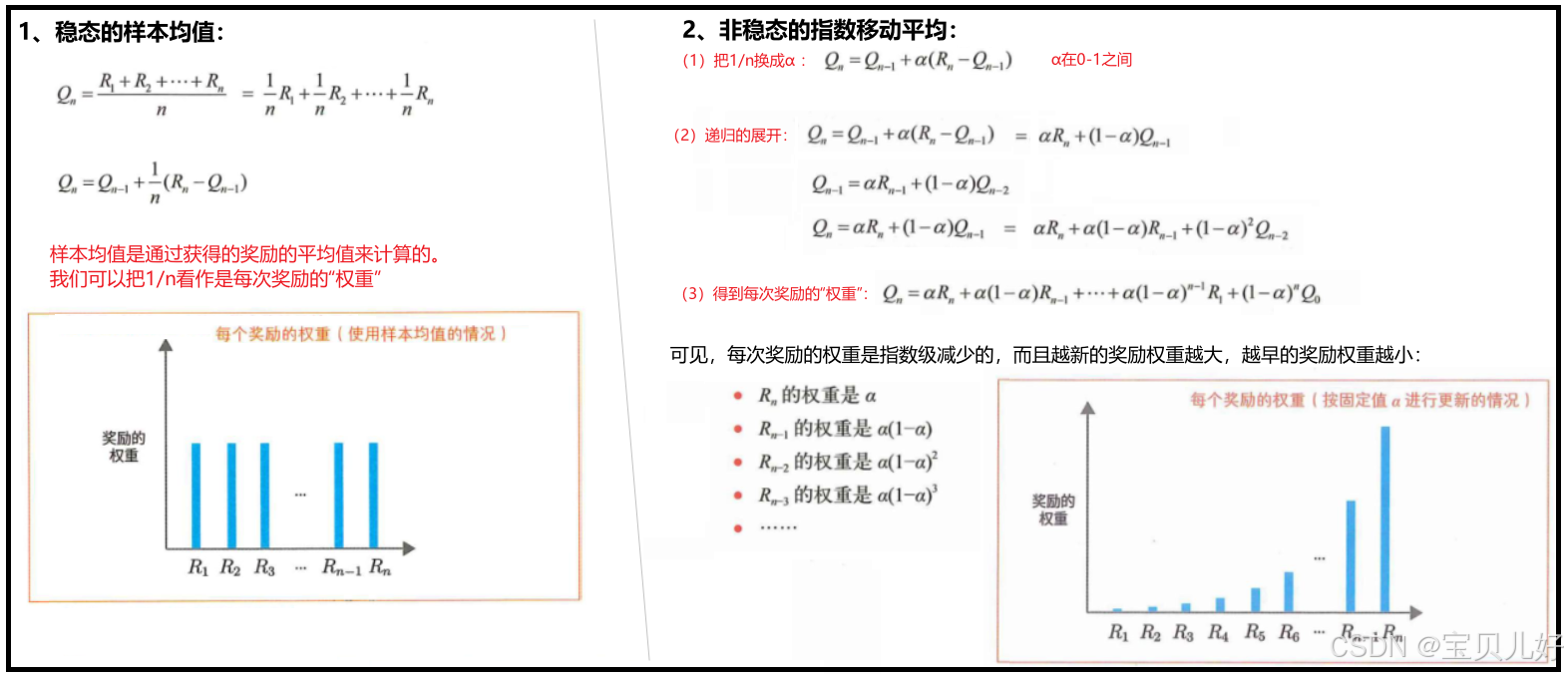

指数移动平均 又叫指数加权移动平均(exponential weighted moving average)，它可以为新获得的数据赋予更大的权重。我们可以用它来计算行动价值的估计值。下面我用代码来实现：

#指数移动平均   
class Env:
    def __init__(self, set_of_tiger):
        np.random.seed(0)
        self.machine_winning_rate = np.random.rand(set_of_tiger)
        self.arms = set_of_tiger
    def reward(self, tiger_index, play_result):            #给老虎机的胜率添加随机性
        self.machine_winning_rate += 0.1*np.random.randn(self.arms)
        if play_result < self.machine_winning_rate[tiger_index]: 
            return 1 
        else:
            return 0 
        
class Agent5:
    def __init__(self, action_times, set_of_tiger, epsilon, alpha): 
        self.ns = np.zeros(set_of_tiger) 
        self.Qs = np.zeros(set_of_tiger) 
        self.epsilon = epsilon
        self.alpha = alpha
        
    def choose_machine(self, set_of_tiger):
        if np.random.rand() < self.epsilon: 
            tiger_index = np.random.randint(0, set_of_tiger)
        else:
            tiger_index = np.argmax(self.Qs)
        return tiger_index
    
    def play(self):
        play_result = np.random.rand() 
        return play_result
        
    def record(self, tiger_index, reward):
        self.ns[tiger_index] += 1
        self.Qs[tiger_index] += (reward-self.Qs[tiger_index])*self.alpha #1/n换成α
        
set_of_tiger=5
num_games = 2500
epsilon = 0.7
alpha = 0.01
env = Env(set_of_tiger=set_of_tiger)
agent5 = Agent5(action_times=num_games, set_of_tiger=set_of_tiger, epsilon=epsilon, alpha=alpha)

for i in range(num_games):
    tiger_index = agent5.choose_machine(set_of_tiger)   #随机选择一台老虎机玩
    play_re = agent5.play()   #玩的结果
    reward_i = env.reward(tiger_index, play_re)  #获得的奖励
    agent5.record(tiger_index, reward_i)   #记录玩的结果
    
print("每台老虎机玩的次数：",  agent5.ns)
print("统计每台老虎机的胜率：", agent5.Qs)
print("agent5打2500轮游戏的奖励总和：", sum(agent5.ns * agent5.Qs))
print("每台老虎机得的奖励是：", agent5.ns * agent5.Qs)

我自己调了很多次epsilon和alpha，个人认为还是epsilon对结果的影响最大。