大模型量化技术全解析,先理解线性量化的基础,再看对象/粒度/流程怎么选,最后是各种进阶招式。
1 为什么大模型必须量化
1.1 不量化,模型连显存都进不去
以 70B 参数模型为例粗算一下:
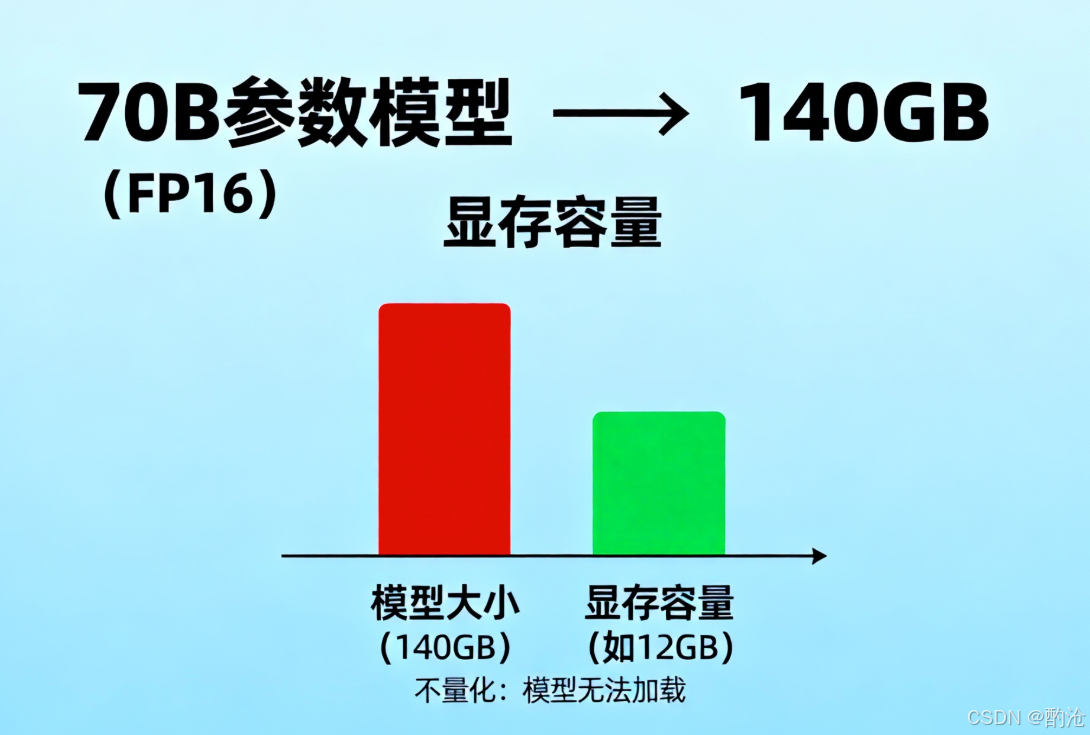
FP16 权重大小:70×109 参数×2 bytes≈140GB70\times10^9 \text{ 参数} \times 2 \text{ bytes} \approx 140\text{GB}70×109 参数×2 bytes≈140GB。推理时还要额外加上:激活、KV cache、多副本、碎片、编译优化带来的冗余......
如果不量化,很多大模型根本塞不进一张卡,连加载模型都是奢望,更别提高并发服务。
1.2 量化带来的现实收益
显存/内存线性缩小:FP16 → INT8:权重理论上减半;FP16 → INT4:权重理论上压到 1/4。
带宽压力显著下降:大模型推理常常是算力闲着、带宽先满,显卡计算过程需要频繁的把模型的参数值和激活值从显存加载到计算单元,计算完成后将结果放回显存。量化减少每次从显存拉数据的字节数,真实吞吐就上来了。
推理成本下降:显卡对整数运算速度快于浮点数,加快模型推理速度。
边缘部署才有可能:手机、嵌入式 NPU、CPU-only 机器,这些场景没量化基本不用想。
2 线性量化的数学模型
2.1 scale+zero-point:连续空间切成台阶
典型线性量化可以写成给定浮点数 (x),映射到整数 (q)

原本连续的实数轴被切成一个个等宽小区间,每个区间对应同一个整数。可以把它想象成把一条平滑曲线强行改成楼梯型的函数。
2.2 对称量化 vs 非对称量化
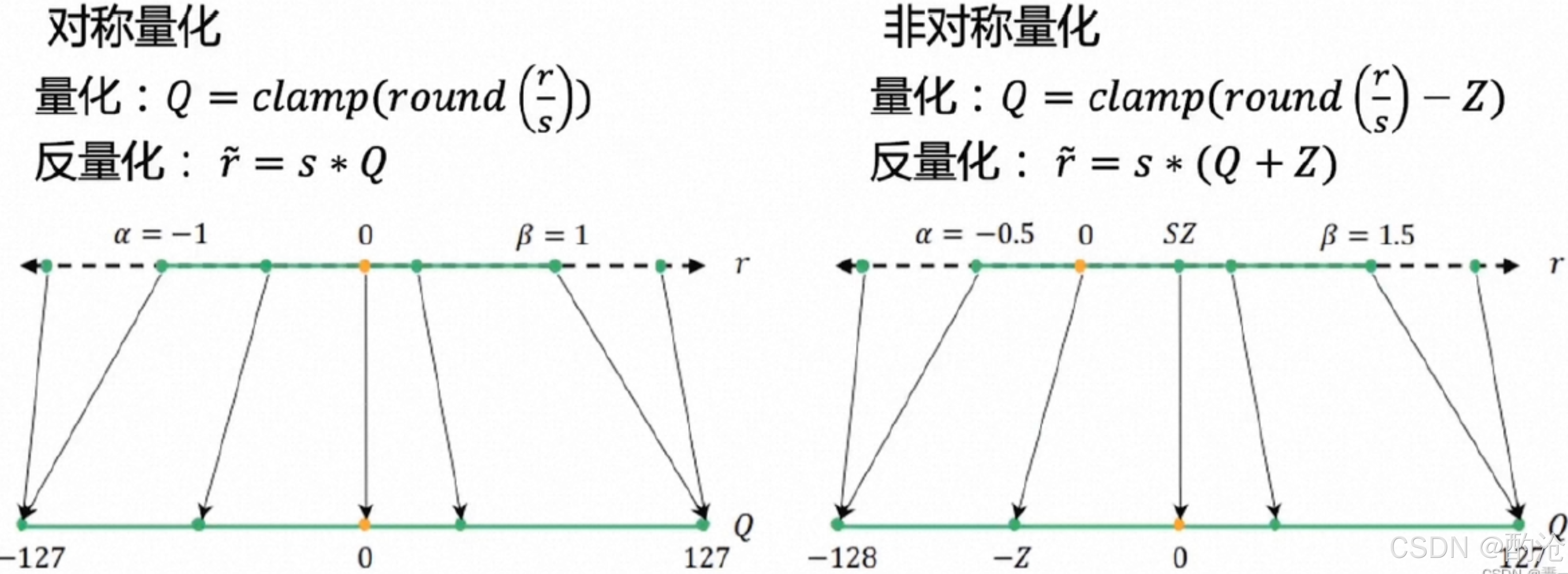
对称量化 :通常设 (z = 0) 或固定在中点;区间近似 ([-a, a]) 对称;优点是公式简单,易用高效整数 MAC;常用场景是权重量化(权重大多近似零均值)。
非对称量化 :(z) 可以不是 0,区间 [xmin,xmax][x_{\min}, x_{\max}][xmin,xmax] 不一定对称;优点是适合激活输出这种整体偏移很大的分布;缺点是硬件实现更复杂,需要额外处理偏移。
3 量化对象与粒度的设计空间
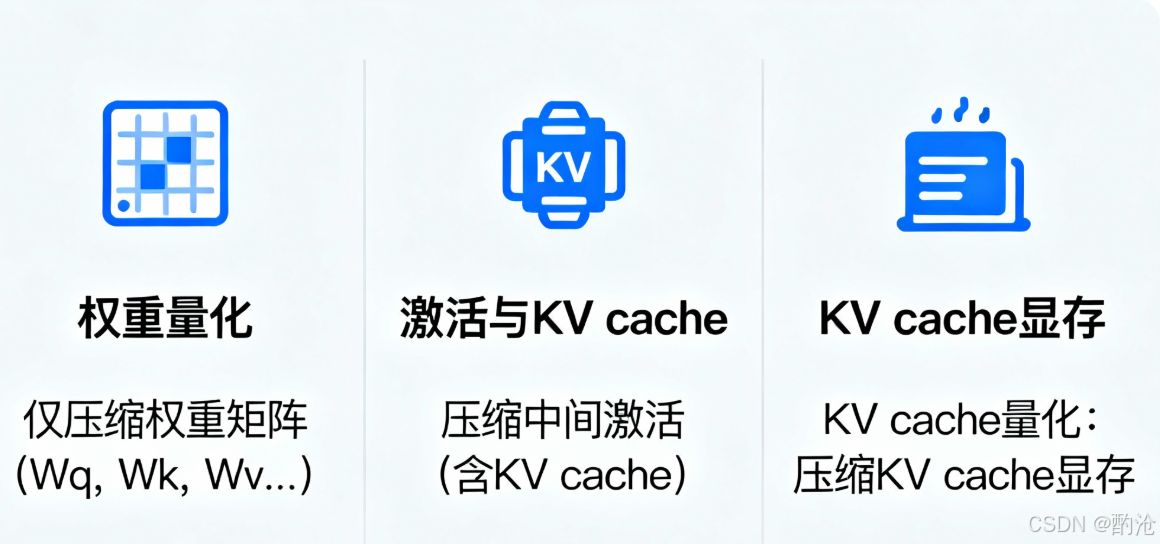
3.1 量化谁:权重vs激活vs V
权重量化:只压缩权重矩阵(Wq, Wk, Wv, W1, W2...);激活仍用 FP16/BF16;特点是最容易落地,也是当前推理部署的主流。
激活量化:中间激活(含 KV cache)也压到低比特;KV cache 显存显著下降;难点是激活分布受输入影响大、极值多,很容易炸。
KV cache 量化:KV cache 大小跟层数 × 头数 × head_dim × 序列长度成正比;长上下文 + 多用户并发时,KV 常常是显存第一大户;把 KV 从 FP16 压到 INT8/INT4,收益非常可观。
3.2 怎么切:tensor/channel/group
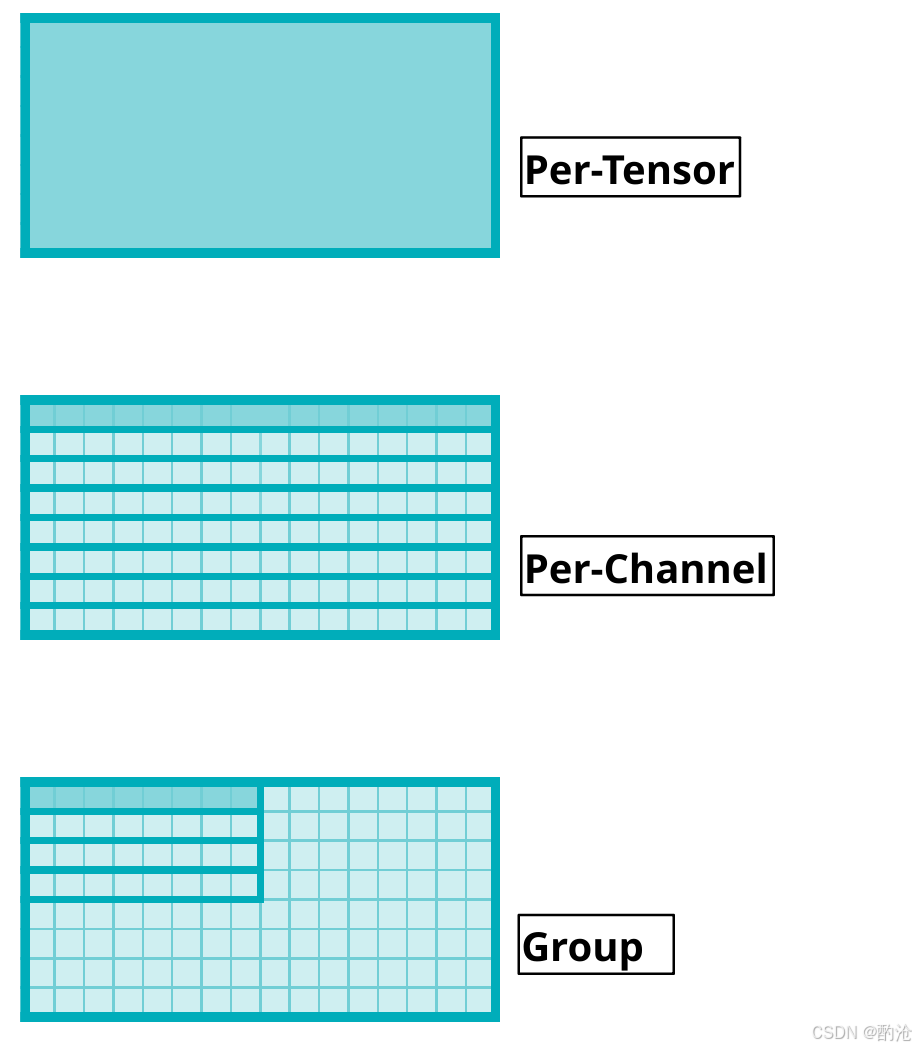
per-tensor 量化:整个矩阵共用一对 scale/zero-point;实现简单,但对 LLM 来说基本精度灾难。
per-channel 量化:(最常用)常见是按输出通道(每一行)独立一个 scale;每个输出神经元的权重分布不同,必须单独标尺;是当前 LLM 权重量化的默认选项。
per-group 量化:在一行内部按列分组,例如 group size = 32:每 32 个权重共用一个 scale;小 group精度好但需要多存 scale;大 group存储节省但误差更大;常见于 4bit/3bit 的折中设计。
混合粒度 / 混合精度:对关键层/关键通道抬高位宽或缩小 group;例如embedding / lm_head 用 8bit,其它层用 4bit;或者 Q/K 用更高精度,其它随缘。
3.3 何时做:PTQ vs QAT
PTQ(后训练量化):用一小批校准数据跑前向,收集分布信息(min/max、直方图等);然后一次性为每层算出 scale / zero-point;GPTQ 等会在这个阶段做局部优化;优点是不需要训练、不需要梯度。
QAT(量化感知训练):在训练/微调时引入 fake quant,前向模拟量化、反向用直通估计;模型学会在量化噪声存在的条件下工作精度最好,但成本也最高。
4 Transformer中具体量化什么
在一个标准 Transformer block 里,常见量化对象包括:
线性层权重:Attention:Wq, Wk, Wv, Wo;FFN:W1, W2(以及带 SwiGLU 时的 W3)
中间激活:自注意力的输入/输出、FFN 中间的激活值;常常含有离群值,量化设计要格外小心。
KV cache:尺度跟层数、头数、head 维度、序列长度成正比;长上下文和多用户并发时,KV 显存占比非常夸张。
5 主流量化方法的思路
5.1 GPTQ系:最小化layer输出误差
不要只看分布的 min/max,而是直接用层输出的误差作为优化目标。
选定一个线性层权重矩阵 (W),按行/列切成小 block;用一批校准样本前向,记录该层的输入激活 (X) 和输出 Y=XW⊤Y = XW^\topY=XW⊤;对每个 block,在 4bit/8bit 的约束下找量化后的 W^\hat{W}W^,使∣XW^⊤−Y∣2|X\hat{W}^\top - Y|^2∣XW^⊤−Y∣2尽可能小;这等价于在每个 block 上做一个局部二次优化问题。
优点:通常比简单的 min-max 量化精度好很多;在 4bit 权重量化中尤其有效。
缺点:实现相对复杂,校准 + 优化较耗时;不同模型/任务仍要调一些超参。
5.2 AWQ等:关键通道更多预算
在 LLM 中,权重和激活分布常常有少量离群值通道,幅值极大但对输出贡献很大。4bit 一压,这些通道几乎必崩。AWQ 的本质上把有限的量化预算优先用在最影响结果的那部分通道上:
评估通道重要性:找出对层输出影响最大的通道;
对重要通道做特殊处理:保留更高位宽;单独的 scale;先 rescale 到更友好的范围,再在下游层反向缩放回来。
5.3 moothQuant/LLM.int8:激活平滑
激活分布常带有少量巨大离群值。如果量化区间拉得很大,绝大多数小值都挤在中间几个 bin;如果裁掉离群值,又会严重失真。SmoothQuant 的做法非常物理:
对Y=XW⊤Y = XW^\topY=XW⊤在量化前做一个平移负担的变换:$
X' = X \cdot D,\quad W' = D^{-1} W$。其中 DDD 是对角缩放矩阵。变换后Y=X′W′⊤Y = X' W'^\topY=X′W′⊤。
语义不变(数学上完全等价);但激活和权重的分布都变了:激活离群值被压平;权重接受了一点放大负担。
LLM.int8()、各种混合精度方案也是类似直觉:极端值和关键层保留高精度,其他部分压低精度。
5.4 非线性量化码本:NF4
NF4 = Normal Float 4,最早在 QLoRA 工作中提出,用于 4bit 权重量化。线性 INT4 把刻度均匀铺开,浪费大量分辨率在远端尾部。核心有三点:
NF4 不是 int4,而是一种4bit 非均匀浮点格式:线性 INT4是16 个刻度在 [min, max] 内等间距;16 个刻度不均匀分布,刻度点在 0 附近更密、两端更稀疏,去拟合标准正态分布。
实际存的是索引,用查表还原值 :预先定义一个长度为 16 的查找表LUT=[v0,v1,...,v15]\text{LUT} = [v_0, v_1, \dots, v_{15}]LUT=[v0,v1,...,v15],这些 viv_ivi是针对高斯权重优化出的 16 个非均匀刻度。每个权重只在 0~15 里选一个 index 存起来。
再配合 block-wise 的线性变换 :对每个 block(比如 64/128 个权重为一组)估计均值和缩放 x~=x−μα\tilde{x} = \frac{x - \mu}{\alpha}x~=αx−μ,将x~\tilde{x}x~映射到 NF4 的刻度点上,选择最近的viv_ivi;反量化时x^=α⋅vindex+μ\hat{x} = \alpha \cdot v_{\text{index}} + \mux^=α⋅vindex+μ。
假设权重满足 w∼N(0,σ2)w \sim \mathcal{N}(0, \sigma^2)w∼N(0,σ2):信息论告诉我们最优的量化点应该在高概率区域(靠近 0)更密集,在尾部更稀疏。
6 工程落地:一套量化流程
准备校准数据集:从真实线上日志中采样几千到几万条 prompt;覆盖短问答、长上下文、多轮对话、代码、SQL 等。
前向收集统计信息:用原始 FP16 模型跑一遍校准集;对每层记录输入/输出激活的 min/max、均值、方差、直方图;权重的统计(有些方法直接从 checkpoint 读取)。
确定量化策略:决定位宽8bit 还是 4bit;粒度per-channel + group size;哪些层保持高精度(常见:embedding、lm_head、不稳定的 few 层)。
执行量化:使用选定算法(GPTQ / AWQ / 简单 linear...)生成量化权重;打包成目标格式(如 nibble packing + scale 表)。
离线评估:跑通用 benchmark + 业务特定评测;重点关注长上下文、代码、复杂推理等。
)。
执行量化:使用选定算法(GPTQ / AWQ / 简单 linear...)生成量化权重;打包成目标格式(如 nibble packing + scale 表)。
离线评估:跑通用 benchmark + 业务特定评测;重点关注长上下文、代码、复杂推理等。