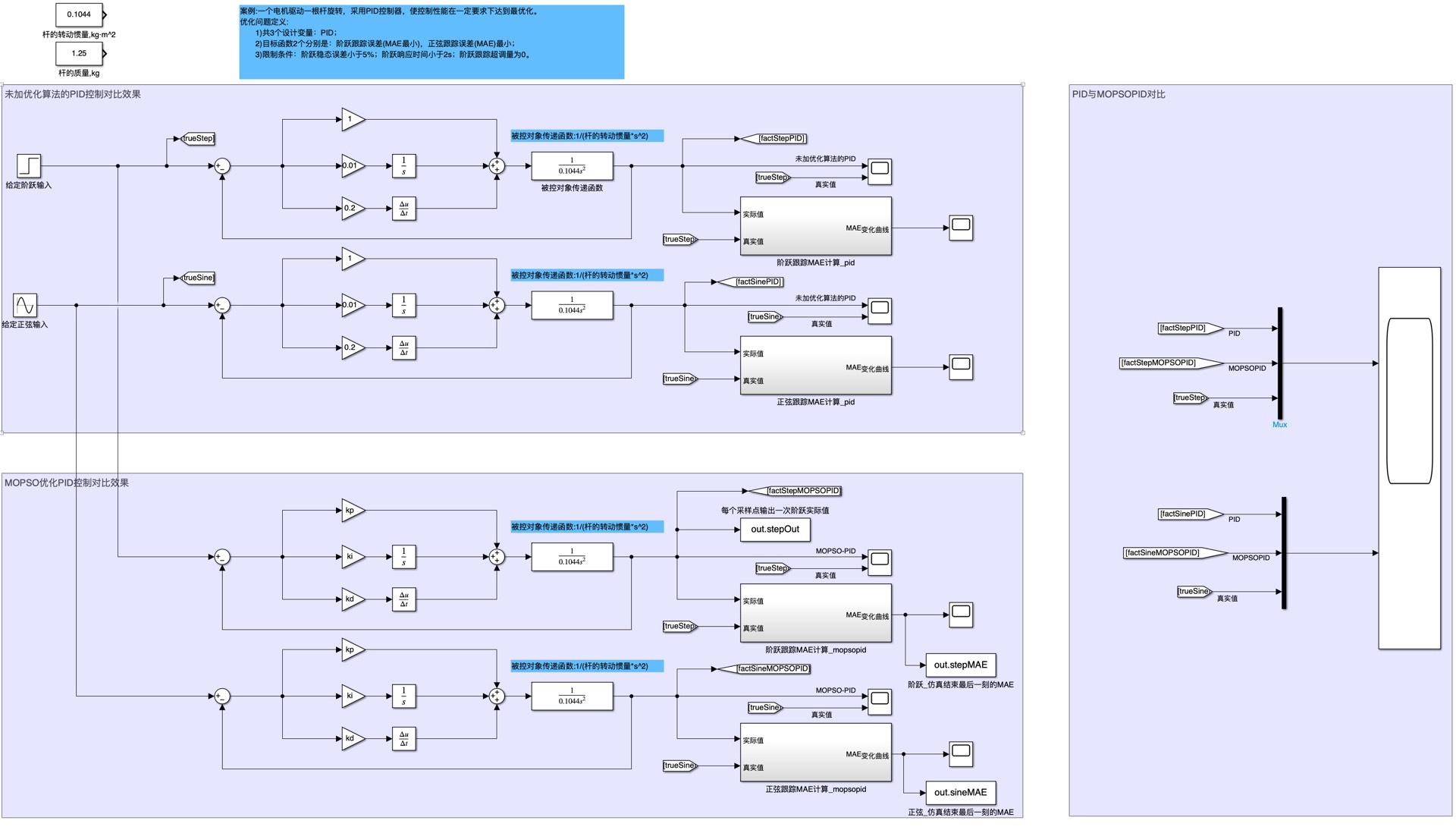
MOPSO-PID：多目标粒子群优化PID的探索之旅

MOPSO-PID/多目标粒子群优化PID/Simulink多目标粒子群整定PID参数/MOPSO寻优多目标PID参数传统粒子群整定PID参数的适应度目标只有一个(如ITAE指标)，如果想综合考虑被控对象的超调、响应速度、误差等指标，就需要运用到多目标粒子群算法来权衡选择。内容含1）MOPSO文件夹，适合先了解MOPSO算法；2）MOPSO-PID文件夹，将MOPSO运用到多目标PID参数整定中，选取了两个目标函数，并在结果选择中添加了三种限制条件，便于在非劣解集中选择最优解。两个文件夹互相独立，可非开运行。采用matlab编写代码和simulink搭建模型，代码含详细注释，附带一个说明文档。

在控制领域，PID控制器以其简单易用却又效果显著而广泛应用。然而，如何精准地整定PID参数，一直是工程师们需要攻克的难题。传统粒子群整定PID参数的方法，往往只聚焦于一个适应度目标，比如ITAE指标。但在实际工程里，我们常常希望能综合考量被控对象的超调、响应速度以及误差等多个重要指标，这时候，多目标粒子群算法（MOPSO）就闪亮登场了，它能够帮助我们在这些指标间进行权衡选择。

MOPSO算法初探

首先介绍一下MOPSO文件夹，这个文件夹是了解MOPSO算法的绝佳起点。MOPSO算法相较于传统粒子群算法，它不再局限于单一目标的优化，而是能够同时处理多个相互冲突的目标。

这里简单给大家看一段基础的粒子群算法代码（以单目标为例，方便理解原理）：

matlab 复制代码

% 初始化参数
pop_size = 50; % 种群大小
dim = 2; % 维度，对应PID的P、I、D参数
max_iter = 100; % 最大迭代次数
c1 = 1.5; % 学习因子1
c2 = 1.5; % 学习因子2
w = 0.9; % 惯性权重
w_damp = 0.99; % 惯性权重递减率
% 初始化粒子位置和速度
x = rand(pop_size, dim);
v = rand(pop_size, dim);
% 个体最优位置
pbest = x;
% 个体最优适应度
pbest_fitness = Inf(pop_size, 1);
% 全局最优位置
gbest = [];
% 全局最优适应度
gbest_fitness = Inf;

for iter = 1:max_iter
    % 计算适应度
    fitness = calculate_fitness(x);
    % 更新个体最优
    index = fitness < pbest_fitness;
    pbest(index, :) = x(index, :);
    pbest_fitness(index) = fitness(index);
    % 更新全局最优
    [min_fitness, min_index] = min(pbest_fitness);
    if min_fitness < gbest_fitness
        gbest_fitness = min_fitness;
        gbest = pbest(min_index, :);
    end
    % 更新速度和位置
    v = w * v + c1 * rand(pop_size, dim).*(pbest - x) + c2 * rand(pop_size, dim).*(repmat(gbest, pop_size, 1) - x);
    x = x + v;
    % 限制位置范围
    x = max(0, min(1, x));
    % 更新惯性权重
    w = w * w_damp;
end

这段代码实现了基本的粒子群算法流程。初始化粒子的位置和速度，在每次迭代中，通过比较当前适应度和个体最优适应度来更新个体最优位置，再从个体最优中找出全局最优。然后依据惯性权重、学习因子来更新粒子的速度和位置，并且限制粒子位置在一定范围内。MOPSO算法则是在此基础上，针对多目标情况进行了拓展。

MOPSO - PID：多目标PID参数整定实战

接下来看看MOPSO - PID文件夹，这里将MOPSO算法成功运用到了多目标PID参数整定中。在这个过程里，选取了两个目标函数，这两个目标函数分别从不同角度反映了系统性能，比如一个侧重于超调的控制，另一个则更关注响应速度。

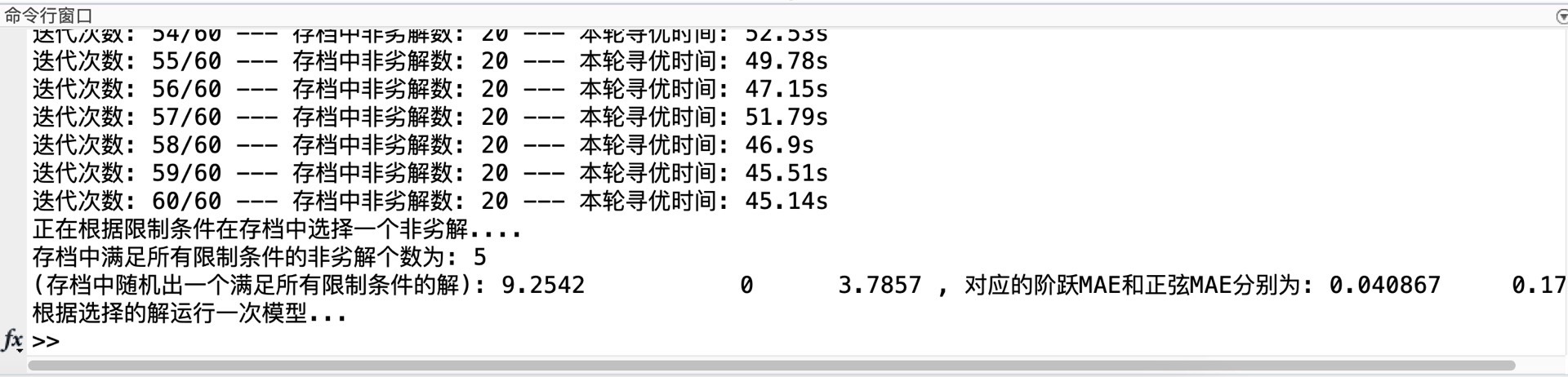
在结果选择方面，添加了三种限制条件，这极大地方便了我们在非劣解集中选择最优解。非劣解集是多目标优化中非常重要的概念，简单说就是这些解之间无法直接比较谁更优，因为它们在不同目标上各有优劣。而通过这三种限制条件，我们能从这个复杂的解集中挑选出最符合我们实际需求的解。

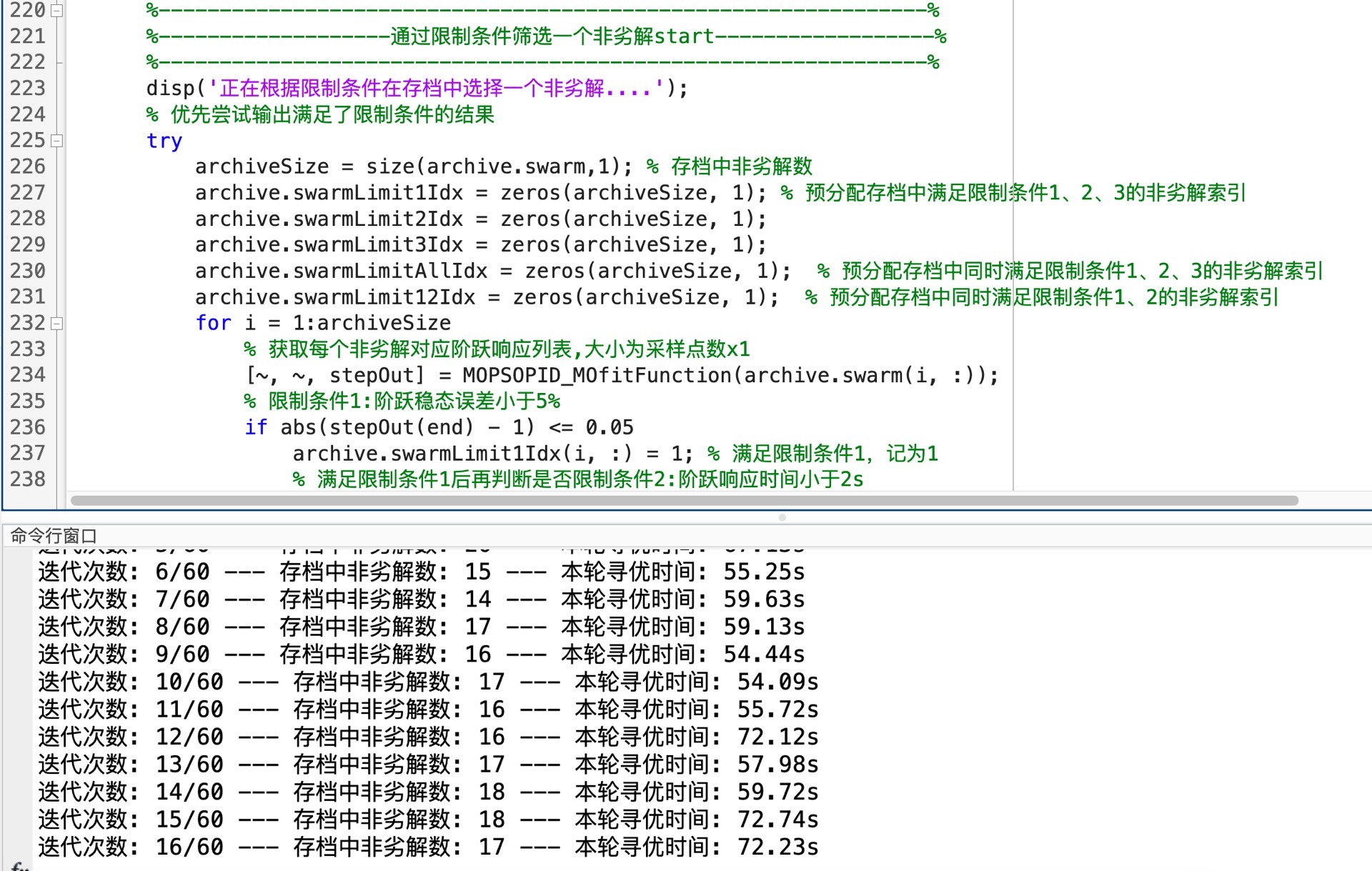
下面是MOPSO - PID的部分核心代码：

matlab 复制代码

% 初始化MOPSO参数
pop_size = 50; % 种群大小
dim = 3; % PID参数维度
max_iter = 100; % 最大迭代次数
% 初始化粒子位置和速度
x = rand(pop_size, dim);
v = rand(pop_size, dim);
% 计算初始目标函数值
obj_values = calculate_obj_functions(x);
% 快速非支配排序
[rank, crowding_distance] = fast_non_dominated_sort(obj_values);
% 找到当前的非劣解集
non_dominated_set = find(rank == 1);

这里初始化了MOPSO用于PID参数整定的相关参数，生成粒子的初始位置和速度后，计算每个粒子对应的目标函数值。然后通过快速非支配排序算法，确定每个粒子的等级以及拥挤距离，从而找出当前的非劣解集。

在Simulink中搭建与MOPSO - PID算法配套的模型也非常关键。通过将MOPSO优化得到的PID参数输入到Simulink搭建的被控对象模型中，就能直观地看到系统的响应情况。

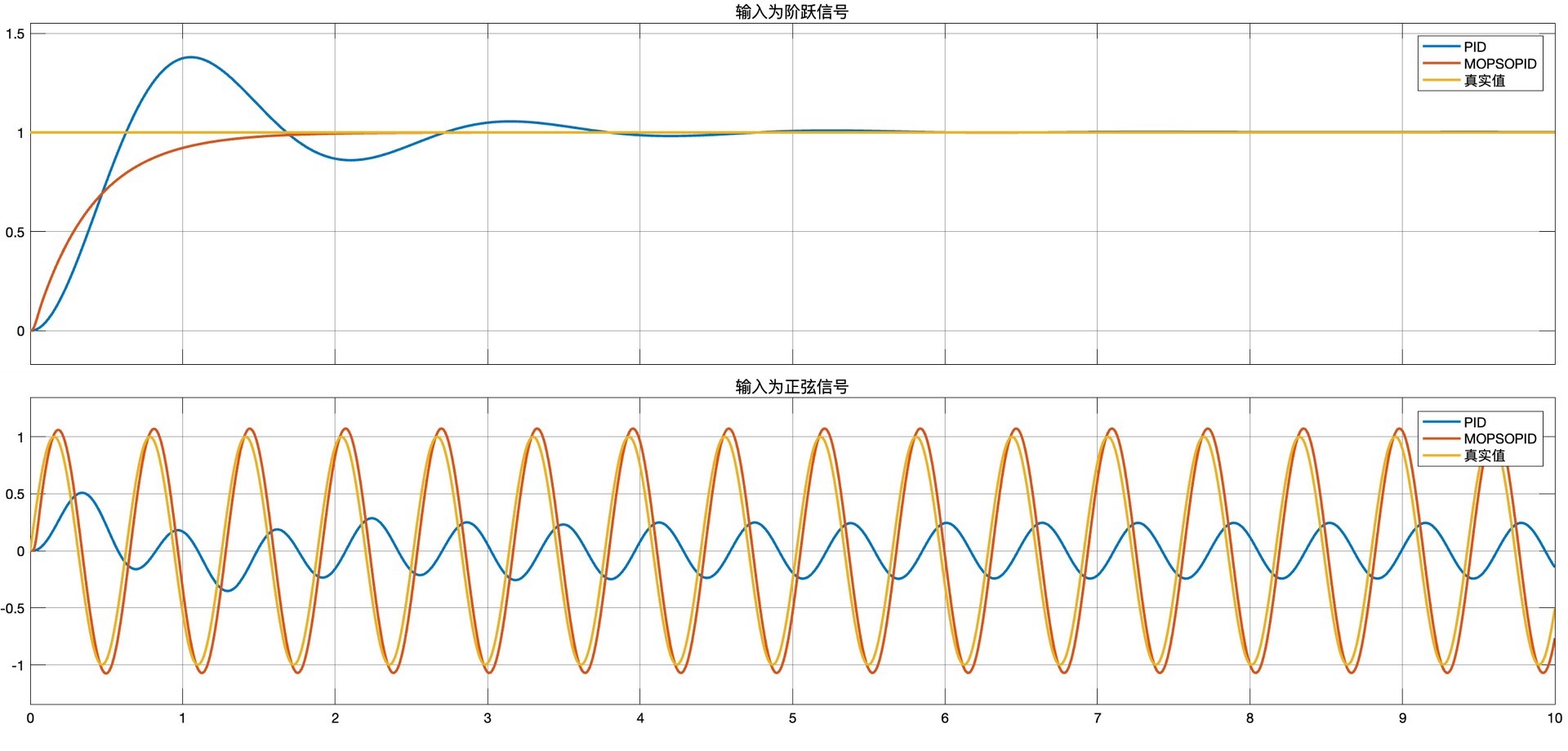
整个项目采用Matlab编写代码，并且代码中包含了详细的注释，同时还附带一个说明文档。这对于想要深入了解算法原理以及如何应用的朋友来说，是非常友好的。就算你是初次接触MOPSO - PID，通过阅读代码注释和说明文档，也能较快上手。

这两个文件夹互相独立，可以分开运行。MOPSO文件夹帮助我们深入理解多目标粒子群算法的精髓，而MOPSO - PID文件夹则是将理论与实际应用相结合，实现了多目标PID参数的整定。希望大家能通过这个项目，对多目标优化以及PID参数整定有更深刻的认识，在实际工程应用中也能更加得心应手。