【算法竞赛】二叉树

🔭 个人主页：散峰而望

《C语言：从基础到进阶》《编程工具的下载和使用》《C语言刷题》《算法竞赛从入门到获奖》《人工智能》《AI Agent》
愿为出海月，不做归山云

🎬博主简介

【算法竞赛】二叉树

前言
[1. 二叉树的概念](#1. 二叉树的概念)
- [1.1 二叉树的定义](#1.1 二叉树的定义)
- [1.2 二叉树的性质](#1.2 二叉树的性质)
- [1.3 特殊的二叉树](#1.3 特殊的二叉树)
- - [1.3.1 满二叉树](#1.3.1 满二叉树)
  - [1.3.2 完全二叉树](#1.3.2 完全二叉树)
[2. 二叉树的存储](#2. 二叉树的存储)
- [2.1 顺序存储](#2.1 顺序存储)
- [2.2 链式存储](#2.2 链式存储)
[3. 二叉树的遍历](#3. 二叉树的遍历)
- [3.1 深度优先遍历](#3.1 深度优先遍历)
- [3.2 宽度优先遍历](#3.2 宽度优先遍历)
结语

前言

二叉树是数据结构与算法竞赛中的核心内容之一，广泛应用于搜索、排序、动态规划等场景。其高效的层次化结构和灵活的遍历方式，为解决复杂问题提供了重要工具。

从基础概念到存储方式，再到遍历算法，掌握二叉树的理论与实现是算法竞赛选手的必备技能。理解满二叉树、完全二叉树等特殊结构的性质，能够帮助优化算法设计；而顺序存储与链式存储的选择，直接影响程序的时空效率。深度优先遍历和宽度优先遍历作为经典算法，不仅是解决二叉树问题的关键，也为图论等其他领域奠定基础。

本文系统梳理二叉树的核心知识点，结合算法竞赛的实际需求，提供清晰的理论框架和实用的代码示例，助力读者高效掌握这一重要数据结构。

1. 二叉树的概念

1.1 二叉树的定义

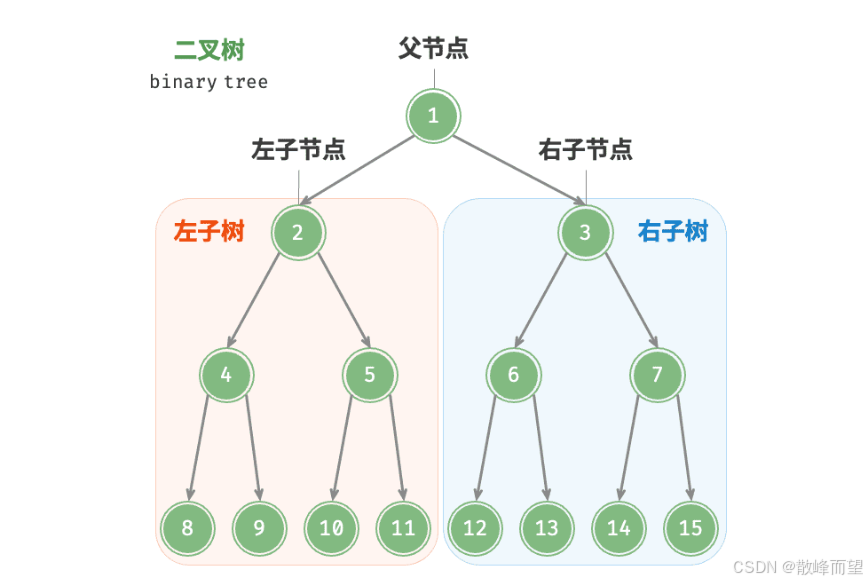
二叉树（binary tree）是一种非线性数据结构，一种特殊的树型结构。与链表类似，二叉树的基本单元是节点，每个节点包含值、左子节点引用和右子节点引用。

每个节点都至多只有 2 个引用（指针），分别指向左子节点和右子节点，该节点被称为这两个子节点的父节点。当给定一个二叉树的节点时，我们将该节点的左子节点及其以下节点形成的树称为该节点的左子树，同理可得右子树。

二叉的意思是这种树的每一个结点最多只有两个孩子结点。注意这里是最多有两个孩子，也可能没有孩子或者是只有一个孩子。

二叉树的子树有左右之分，其次序不能任意颠倒。

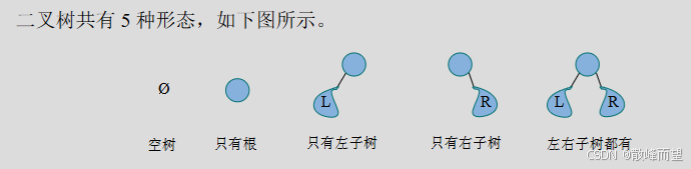
1.2 二叉树的性质

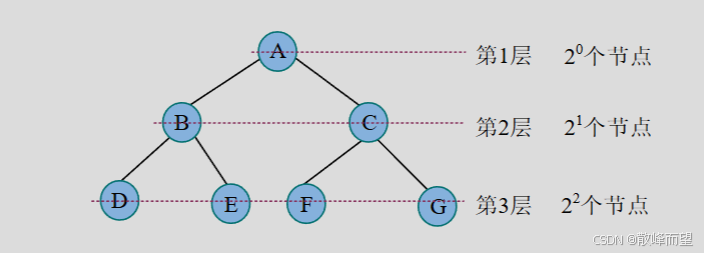
性质 1：在二叉树的第 i 层上至多有 2^(i-1) 个节点

一棵二叉树如下图所示。由于二叉树的每个节点最多有 2 个孩子，第 1 层树根为 1 个节点，

第 2 层最多为 2 个节点，第 3 层最多有 4 个节点，因为上一层的每个节点最多有 2 个孩子，因

此当前层最多是上一层节点数的两倍。

性质 2：深度为 k 的二叉树至多有 (2^k)-1个节点

∑ i = 1 k 2 i − 1 = 2 0 + 2 1 + ⋯ + 2 k − 1 = 2 k − 1 \sum_{i=1}^k 2^{i-1} = 2^0 + 2^1 + \cdots + 2^{k-1} = 2^k - 1 i=1∑k2i−1=20+21+⋯+2k−1=2k−1

性质 3：对于任何一棵二叉树，若叶子数为 n0，度为 2 的节点数为 n2，则 n0=n2+1
（节点的度：节点拥有的子树个数。树的度：树中节点的最大度数。)

证明：二叉树中的节点度数不超过 2，因此共有 3 种节点：度为 0、度为 1、度为 2。设二

叉树总的节点数为 n，度为 0 的节点数为 n0，度为 1 的节点数为 n1，度为 2 的节点数为 n2，总

节点数等于三种节点数之和，即 n=n0+n1+n2。

而总节点数又等于分支数 b+1，即 n=b+1。为什么呢？如下图所示，从下向上看，每一个

节点都对应一个分支，只有树根没有对应的分支，因此总的节点数为分支数 b+1。

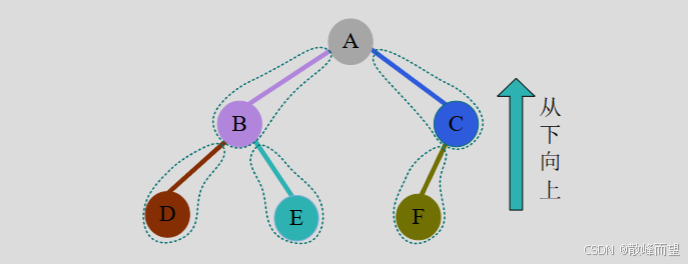
而分支数b怎么计算呢？从上向下看，如下图所示，每个度为 2 的节点都产生 2 个分支，

度为 1 的节点产生 1 个分支，度为 0 的节点没有分支，因此分支数 b=n1+2n2，则n=b+1=n1+2n2+1。

而前面已经得到 n=n0+n1+n2，两式联合得：n0=n2+1。

性质 4：具有 n 个节点的完全二叉树的深度必为 ⌊log2n⌋＋1

1.3 特殊的二叉树

1.3.1 满二叉树

一棵二叉树的所有非叶子节点都存在左右孩子并且所有叶子节点都在同一层上，那么这棵树就称为满二叉树，又称完全二叉树。

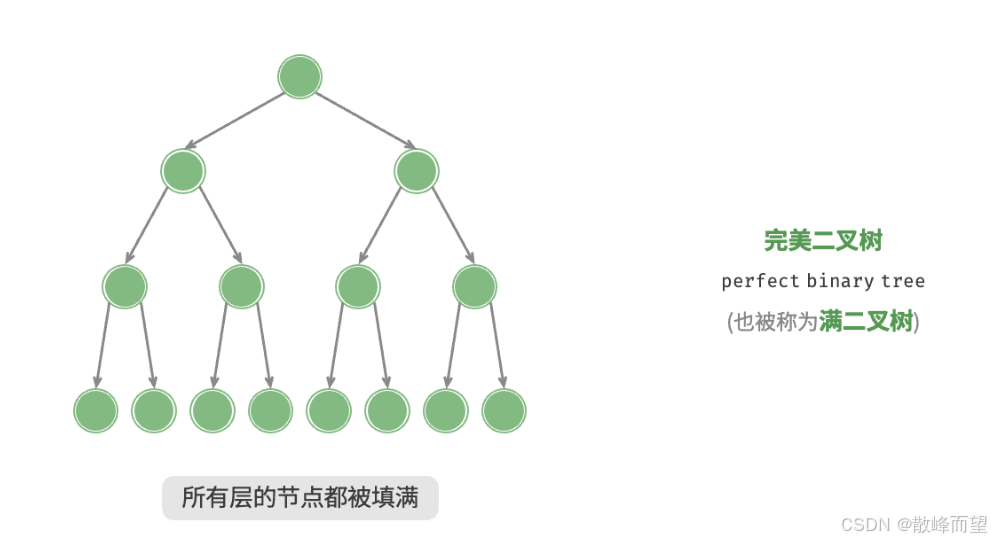
满二叉树的一些性质：

节点为 i 的左孩子的编号为 2 * i
节点为 i 的右孩子的编号为 2 * i + 1
节点 i 的双亲的编号为 i / 2

1.3.2 完全二叉树

对一棵树有 n 个结点的二叉树按层序编号，所有的结点的编号从 1~n 。如果这棵树所有结点和同

样深度的满二叉树的编号为从 1~n 的结点位置相同，则这棵二叉树为完全二叉树。

说白了，就是在满二叉树的基础上，在最后一层的叶子结点上，从右往左依次删除若干个结点，剩下的就是一棵完全二叉树。

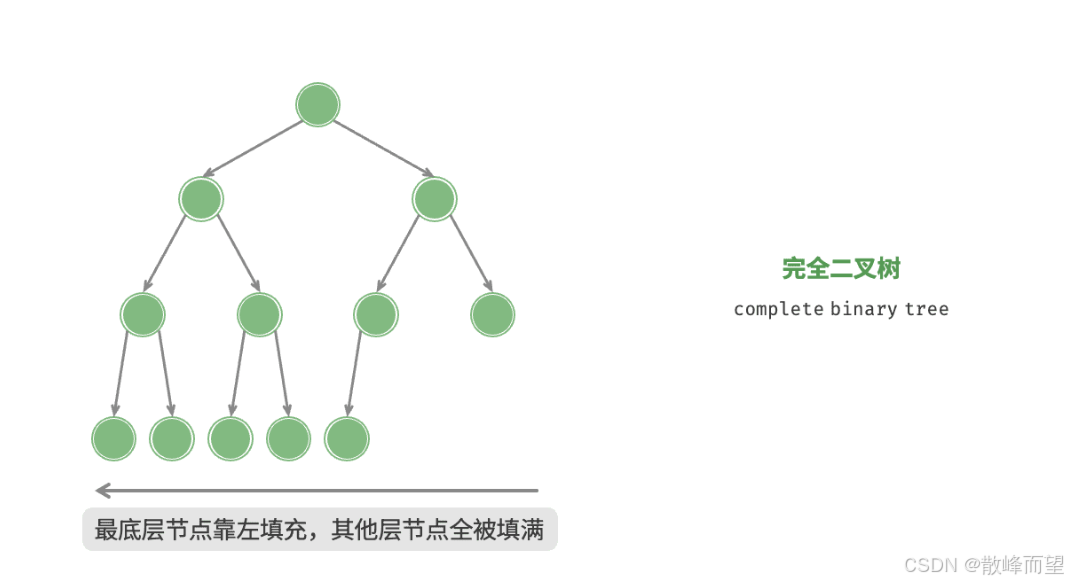
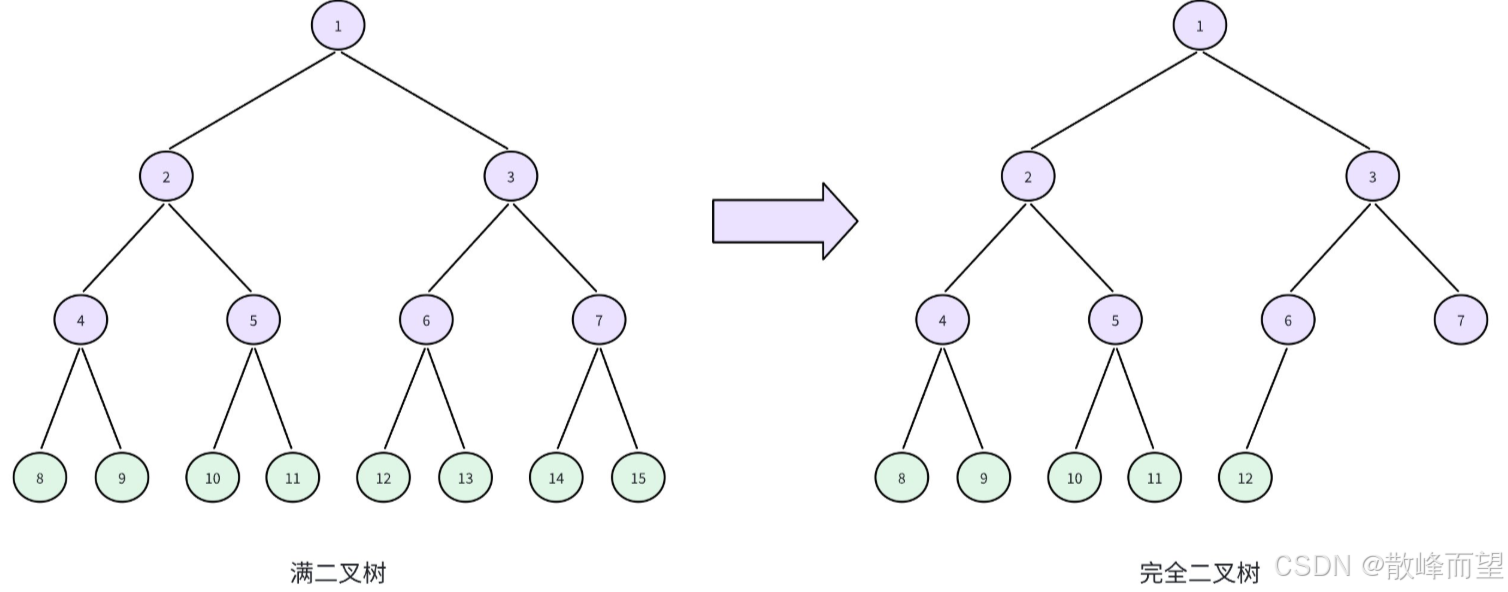
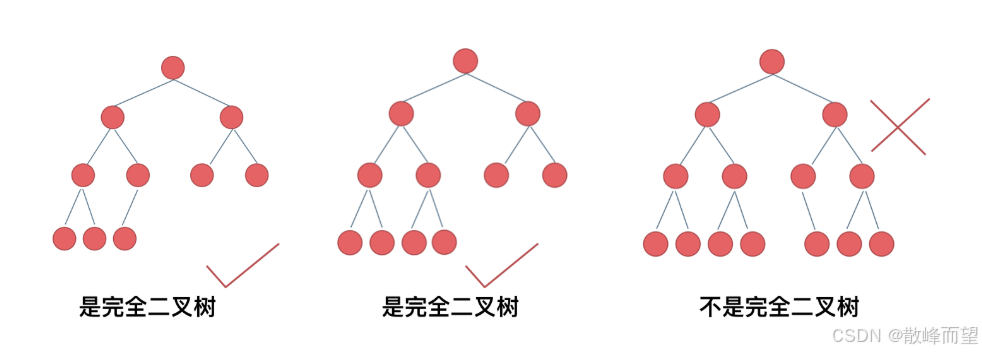
完全二叉树的一些性质：

节点为 i 的左孩子的编号为 2 * i
节点为 i 的右孩子的编号为 2 * i + 1
节点 i 的双亲的编号为 i / 2

除了上述两种二叉树，还有堆、二叉排序树、平衡二叉树、红黑树等，会在后续进行介绍。

2. 二叉树的存储

在【算法竞赛】树中，我们已经知道如何遍历树了，二叉树也是树，也是可以用 vector数组或者链式前向星来存储。仅需在存储的过程中标记谁是左孩子，谁是右孩子即可。

比如用 vector 数组存储时，可以先尾插左孩子，再尾插右孩子；
用链式前向星存储时，可以先头插左孩子，再头插右孩子。只不过这样存储下来，遍历孩子的时候先遇到的是右孩子，这点需要注意。

但是，由于二叉树结构的特殊性，我们除了用上述两种方式来存储，还可以用符合二叉树结构特性的方式：分别是顺序存储和链式存储。

2.1 顺序存储

顺序结构存储就是使用数组来存储。

在完全二叉树以及满二叉树的性质那里，我们了解到：如果从根节点出发，按照层序遍历的顺序，由 1 开始编号，那么父子之间的编号是可以计算出来的。那么在存储完全二叉树的时候，就按照编号，依次放在数组对应下标的位置上，然后通过计算找到左右孩子和父亲：

结点下标为 i ：

如果父存在，父下标为 i / 2

如果左孩子存在，左孩子下标为 i * 2

如果右孩子存在，右孩子下标为 i * 2 + 1

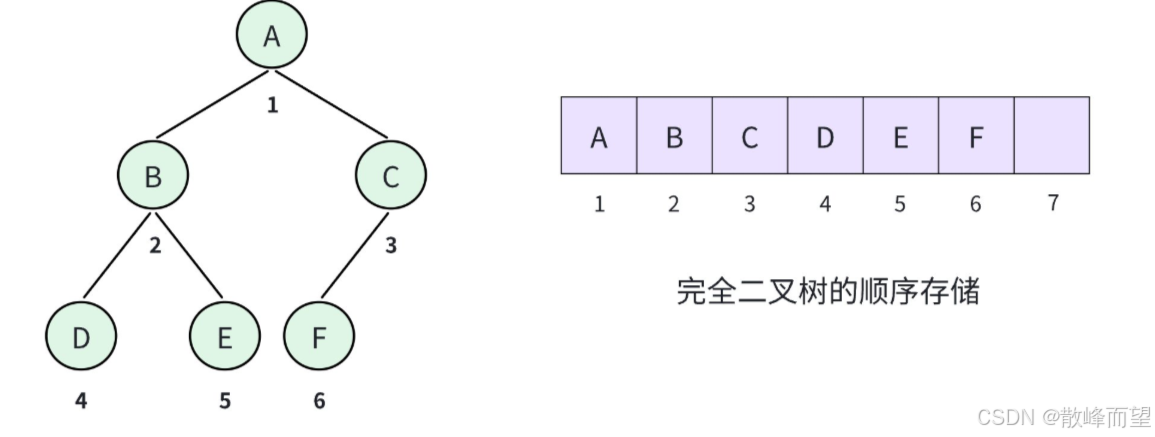
如果不是完全二叉树，也是可以用顺序存储。但是首先要先把这棵二叉树补成完全二叉树，然后再去编号。不然就无法通过计算找到左右孩子和父亲的编号。

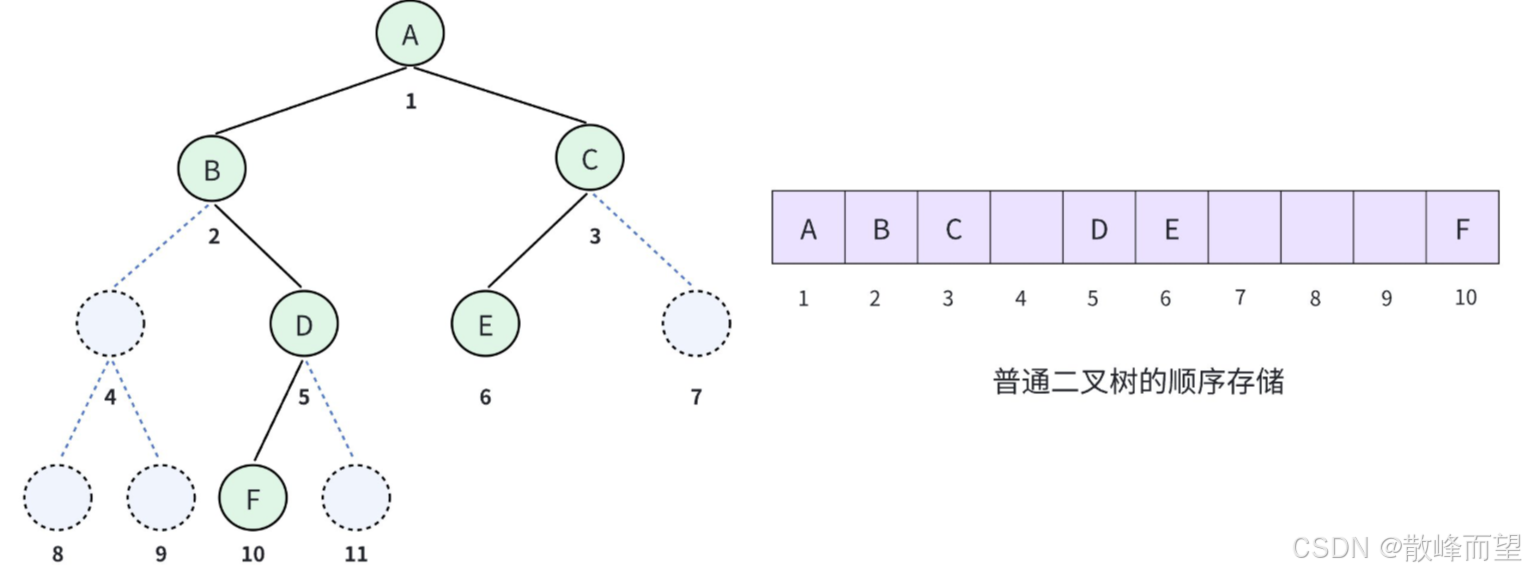
可以看到我们的二叉树其实只有 6 个节点，但是顺序存储却要分配 10 个空间，其中有 4 个空间都被浪费掉了。

有一种极端的情况，整棵树为一棵树右斜树，这显然会对存储空间造成很大的浪费。所以，顺序存储结构一般只用于完全二叉树或满二叉树。

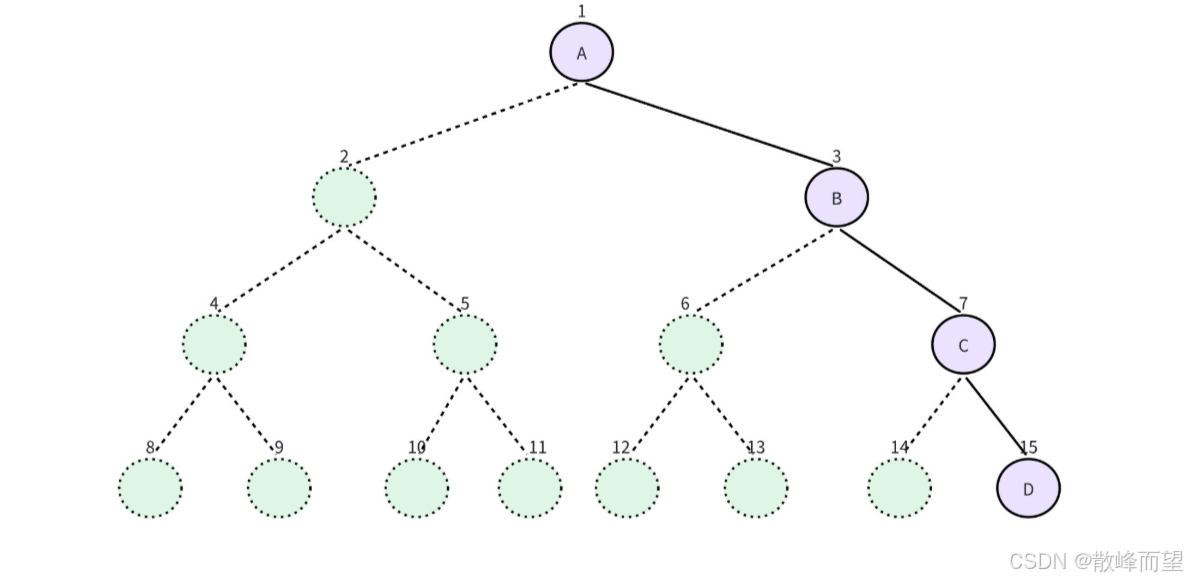
这种存储方式相对简单，按照层序遍历依次往里面填，这里就不做代码展示了。

2.2 链式存储

链式存储类比链表的存储，都有静态实现和动态实现的方式。

我们这里依旧只讲静态实现，也就是用数组模拟。动态实现，就是 new 和 delete 的方式，可以自行了解一下。

竞赛中给定的树结构一般都是有编号的，参考上一章的树结构。因此我们可以创建两个数组 l[N]，

r[N]，其中 l[i] 表示结点号为 i 的结点的左孩子编号，r[i] 表示结点号为 i 的结点的右孩子编号。这样就可以把二叉树存储起来。

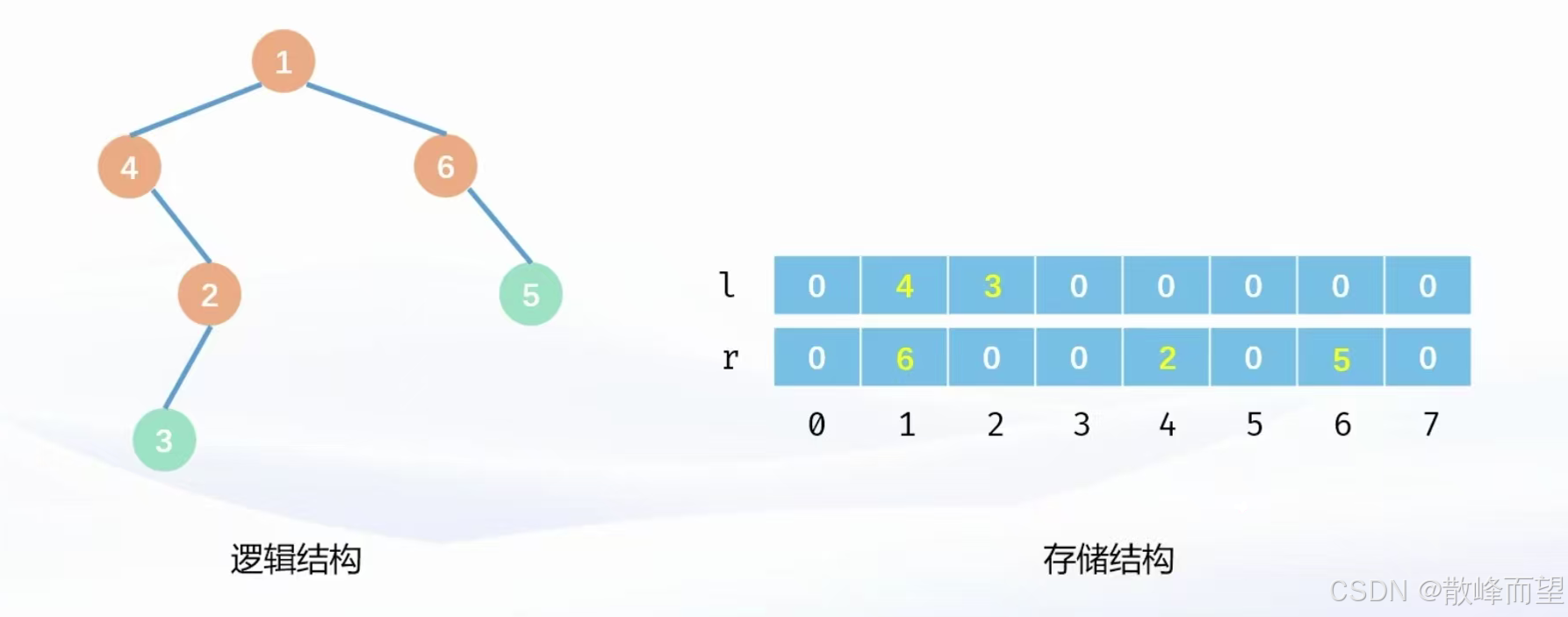
案例：

题目描述：

有一个 n(n <= 10^6) 个结点的二叉树。给出每个结点的两个子结点编号（均不超过 n），建立一棵二叉树（根节点的编号为 1），如果是叶子结点，则输入 0 0

输入描述：

第一行一个整数 n，表示结点数。

之后 n 行，第 i 行两个整数 l 、r ，分别表示结点 i 的左右子结点编号。若 l = 0 则表示无左子结点，r = 0 同理。

代码实现：

cpp 复制代码

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n;
int l[N], r[N];

int main()
{
	cin >> n;
	for(int i = 1; i <= n; i++)
	{
		cin >> l[i] >> r[i];
	}
	return 0;
}

3. 二叉树的遍历

3.1 深度优先遍历

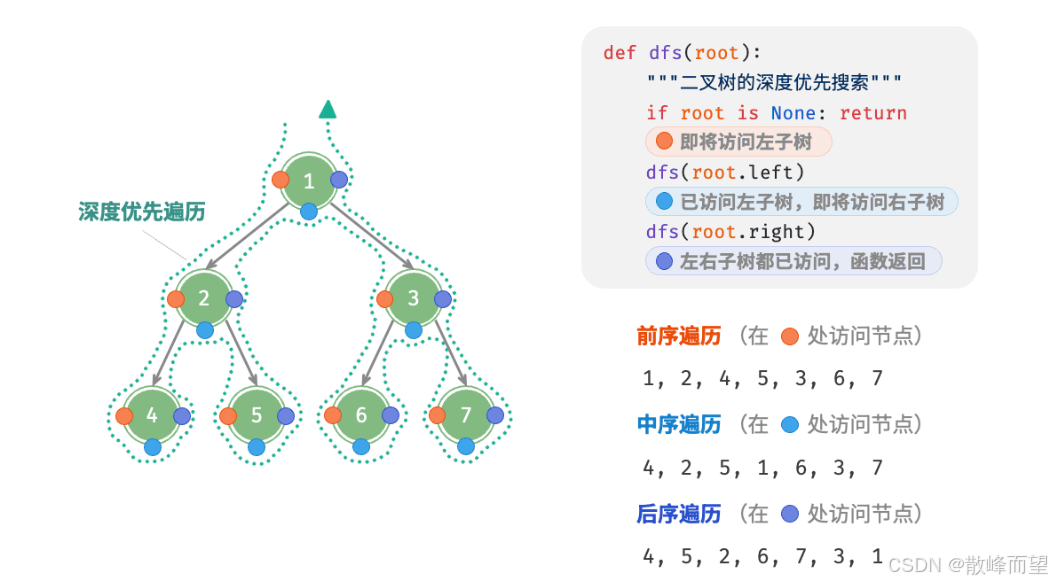
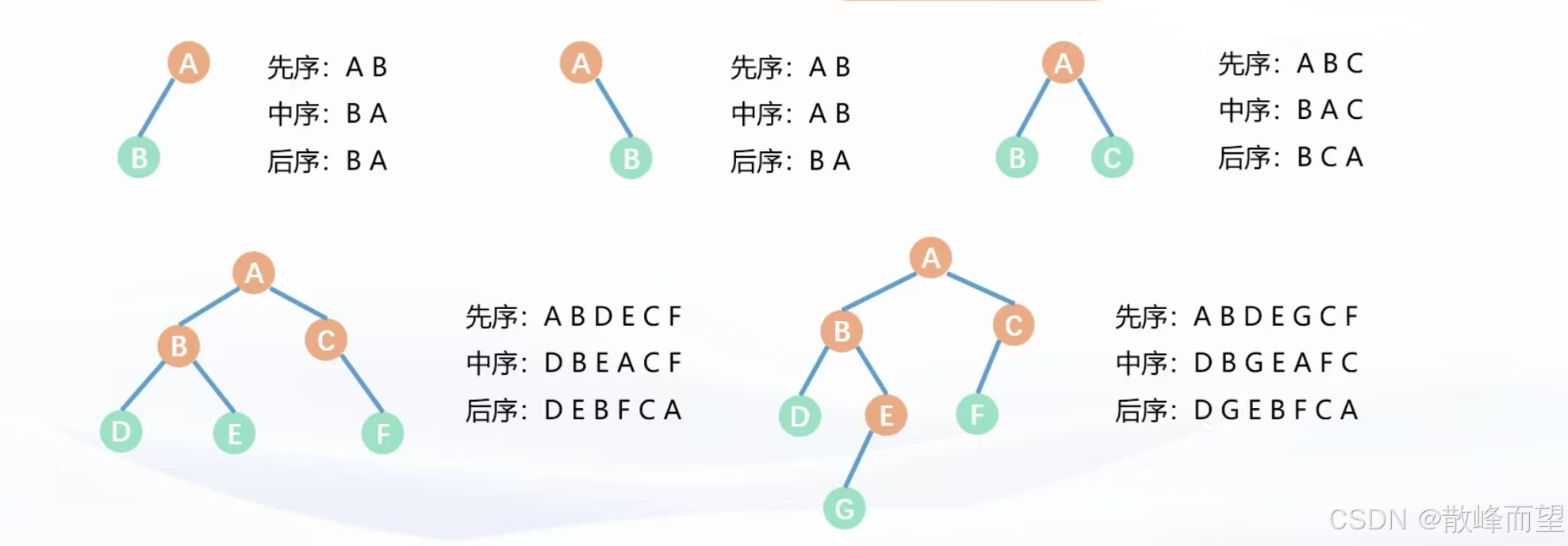
不同于常规树的深度优先遍历，二叉树因其独特的性质可以划分成三种深度优先遍历：先序遍历，中序遍历，和后序遍历。其中，三种遍历方式的不同在于处理根节点的时机。

对于一棵二叉树而言，整体可以划分成三部分：根节点 + 左子树 + 右子树：

• 先序遍历的顺序为：根 + 左 + 右；

• 中序遍历的顺序为：左 + 根 + 右；

• 后序遍历的顺序为：左 + 右 + 根。

案例：

题目描述：

有一个 n(n <= 10^6) 个结点的二叉树。给出每个结点的两个子结点编号（均不超过 n），建立一棵二叉树（根节点的编号为 1），如果是叶子结点，则输入 0 0

输入描述：

第一行一个整数 n，表示结点数。

之后 n 行，第 i 行两个整数 l 、r ，分别表示结点 i 的左右子结点编号。若 l = 0 则表示无左子结点，r = 0 同理。

测试用例：

测试一：

4

0 2

3 4

0 0

0 0

测试二：

2

2 0

0 0

测试三：

3

2 3

0 0

0 0

代码实现：

cpp 复制代码

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n;
int l[N], r[N];

void dfs1(int p)
{
	if(p == 0) return;
	
	//先处理根节点
	cout << p << " ";
	//左子树
	if(l[p]) dfs1(l[p]);
	//右子树 
	if(r[p]) dfs1(r[p]); 
}

void dfs2(int p)
{
	if(p == 0) return;
	
	//左子树
	if(l[p]) dfs2(l[p]);
	cout << p << " ";
	//右子树 
	if(r[p]) dfs2(r[p]); 
}

void dfs3(int p)
{
	if(p == 0) return;
	
	//左子树
	if(l[p]) dfs3(l[p]);
	//右子树 
	if(r[p]) dfs3(r[p]); 
	cout << p << " ";
}

int main()
{
	cin >> n;
	for(int i = 1; i <= n; i++)
	{
		cin >> l[i] >> r[i];
	}
    
	//先序
	dfs1(1);
	cout << endl;
	
	//中序
	dfs2(1);
	cout << endl;
	
	//后序
	dfs3(1);
	cout << endl; 
}

测试结果：

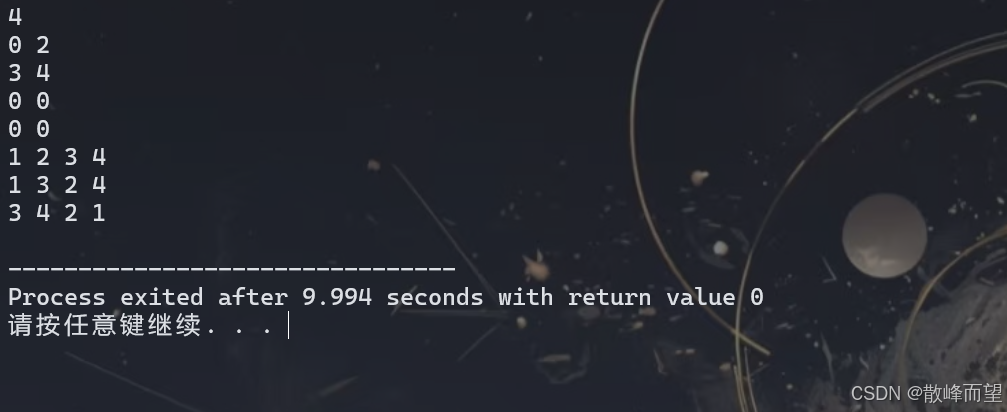
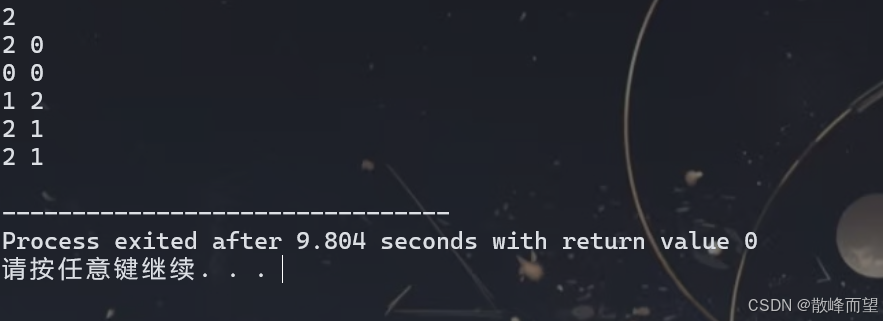
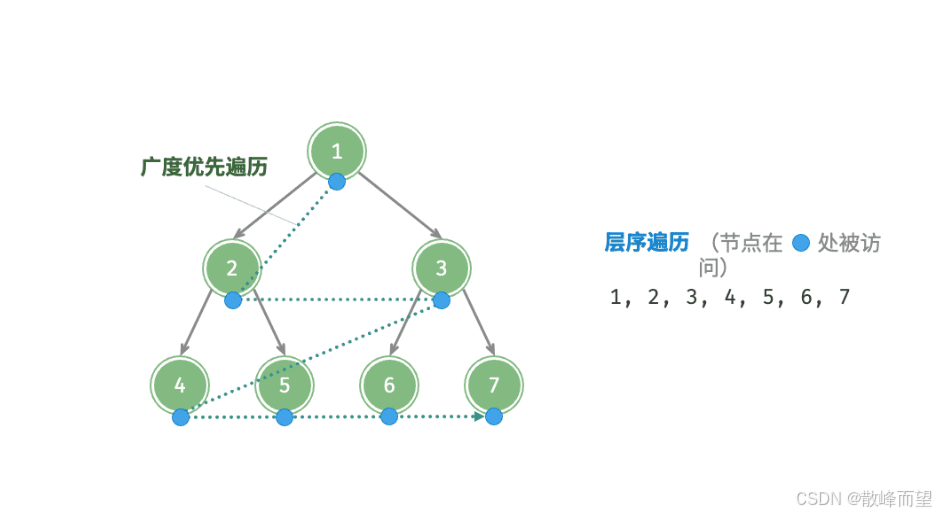
3.2 宽度优先遍历

这个就和常规的树的遍历方式一样，直接用队列帮助层序遍历即可。

代码实现：

cpp 复制代码

#include <iostream>
#include <queue>

using namespace std;

const int N = 1e6 + 10;

int n;
int l[N], r[N];

void bfs()
{
	queue<int> q;
	q.push(1);
	
	while(q.size())
	{
		auto p = q.front(); q.pop();
		cout << p << " ";
		
		//左右孩子入队列
		if(l[p]) q.push(l[p]);
		if(r[p]) q.push(r[p]); 
	}
	cout << endl;
}

int main()
{
	cin >> n;
	for(int i = 1; i <= n; i++)
	{
		cin >> l[i] >> r[i];
	}
	
	bfs();
	
	return 0;
 }

测试结果：

结语

二叉树作为数据结构中的核心内容，在算法竞赛和实际开发中具有广泛应用。从基础定义到存储方式，再到遍历方法，掌握二叉树的相关知识是解决复杂问题的关键。

满二叉树和完全二叉树因其特殊性，常出现在高效算法设计中。顺序存储与链式存储各有优劣，需根据具体场景选择。深度优先遍历和宽度优先遍历为处理树形结构提供了系统化的思路，是后续学习图算法的重要基础。

深入理解二叉树的性质与操作，能够为动态规划、搜索优化等高级算法打下坚实基础。持续练习经典问题（如重建二叉树、最近公共祖先等），有助于提升竞赛中的实战能力。

愿诸君能一起共渡重重浪，终见缛彩遥分地，繁光远缀天。