
这个图是不是一个有向无环图(DAG)?
如果有环(比如 A 依赖 B,B 依赖 C,C 又依赖 A),无法毕业
核心思路
如果在递归过程中,发现下一个节点在递归栈中(正在访问中),则找到了环。
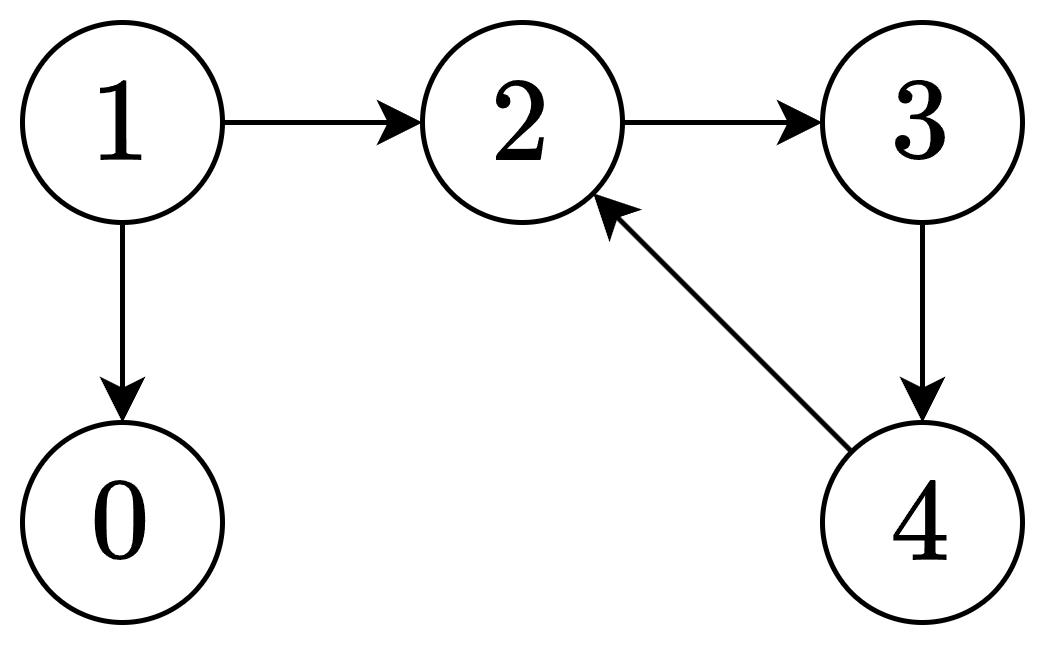
开始节点为:没有前置课程的课程,把题目全部放入队列
- 然后弹出队头,count += 1,表示修完了这门课
- 队头所有的后续课程 -1,同时检查后续课程还有没有前置课程了?没有就加入队列
- 循环弹出,直到没有可以修的课程
- 已经修完的课=总课程数?
需要两个表:
- indegrees(入度表) :"这门课还有多少个前提条件没完成"。
- indegrees[3] = 2,说明课程 3 有 2 门先修课。你现在不能修它
- adjacency(邻接表) :字典,键(Key)是课程 A,值(Value)是一个列表,里面装着所有依赖 A 的课程。
- adjacency[1] = [0]。这意味着:"修完 1 之后,记得去通知 0
例如: 修完B可以修[A,C],邻接表为:
| key | value |
|---|---|
| B | [A,C] |
python
from collections import deque, defaultdict
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
# 1. 统计入度和邻接表
indegrees = [0] * numCourses # "这门课还有多少个前提条件没完成" [0, 0, ...]
adjacency = defaultdict(list) # 依赖课程字典 {0: [], 1: [], ...}
# prerequisites = [[1,0]] 修完0,可以修1
# 想学cur(课程1),必先学pre(课程0)。 边:pre -> cur
for cur, pre in prerequisites:
adjacency[pre].append(cur) # 修完pre,可以修cur
indegrees[cur] += 1 # cur 需要多少先修课
# 2. 将所有不需要先修课的节点入队
q = deque()
for i in range(numCourses): # 遍历每一门课(从 0 到 numCourses - 1)
if indegrees[i] == 0:
q.append(i) # 课程标号入队
# 3. BFS
count = 0 # 统计修完的课程数
while q:
pre = q.popleft()
count += 1 #修完了这门课
# 队头所有的后续课程 -1,同时检查后续课程还有没有前置课程了?没有就加入队列
for cur in adjacency[pre]: # 队头pre的后续课程列表:adjacency[pre]
indegrees[cur] -= 1 # 前置课程-1
if indegrees[cur] == 0: # 没有前置课程了,加入队列
q.append(cur)
# 4. 如果修完的课程数等于总课数,说明无环
return count == numCourses时间复杂度:$O(V + E)
VVV 是课程总数(numCourses),EEE 是先修关系的数量(prerequisites 的长度)。
- 建图阶段:遍历 prerequisites, 填充邻接表和欠债数。这个过程耗时 O(E)O(E)O(E)
- 初始化队列:遍历 indegrees,将所有不需要先修课的节点入队。这个过程耗时 O(V)O(V)O(V)
- BFS 遍历:每个课程(节点)最多进出队列一次,总共 O(V)O(V)O(V)。每当修完一门课,我们会遍历它的"解锁名单"。由于所有名单加起来的总长度就是边的总数,所以这部分总共耗时 O(E)O(E)O(E)
O(E)+O(V)+O(V)+O(E)O(E) + O(V) + O(V) + O(E)O(E)+O(V)+O(V)+O(E),简化后就是 O(V+E)O(V + E)O(V+E)
空间复杂度 :O(V+E)O(V + E)O(V+E)
- adjacency(邻接表):存储了所有的先修关系,空间占用为 O(E)O(E)O(E)。
- indegrees (入度表):存储了 VVV 门课的先修数量,空间占用为 O(V)O(V)O(V)。
- 队列 (Queue):在最坏情况下(比如所有课都是基础课,互不依赖),队列中可能同时存在所有课程,空间占用为 O(V)O(V)O(V)。总计:把这些加起来,空间复杂度同样是 O(V+E)O(V + E)O(V+E)。