648,单词替换
在英语中,我们有一个叫做 词根 (root) 的概念,可以词根 后面 添加其他一些词组成另一个较长的单词------我们称这个词为 衍生词 (derivative )。例如,词根 help,跟随着 继承 词 "ful",可以形成新的单词 "helpful"。
现在,给定一个由许多 词根 组成的词典 dictionary 和一个用空格分隔单词形成的句子 sentence。你需要将句子中的所有 衍生词 用 词根 替换掉。如果 衍生词 有许多可以形成它的 词根 ,则用 最短 的 词根 替换它。
你需要输出替换之后的句子。
代码:
这个代码中,每个单词的子单词都需要和完整的dictionary来匹配,效率很低
python
class Solution:
def replaceWords(self, dictionary: List[str], sentence: str) -> str:
roots = set(dictionary)
new_sent = []
for word in sentence.split():
replaced = False
for i in range(1, len(word) + 1):
if word[:i] in dictionary:
new_sent.append(word[:i])
replaced = True
break
if not replaced:
new_sent.append(word)
return " ".join(new_sent)优化代码:使用前缀树Trie来实现:
python
class TrieNode:
def __init__(self):
self.children = {}
self.is_root = False # 标记是否是一个词根结尾
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
node = self.root
for ch in word:
if ch not in node.children:
node.children[ch] = TrieNode()
node = node.children[ch]
node.is_root = True
def find_prefix(self, word):
node = self.root
prefix = ""
for ch in word:
if ch not in node.children:
return word # 没找到字根 原样返回
node = node.children[ch]
prefix += ch
if node.is_root: # 找到最近的词根
return prefix
return word # 遍历完也没遇到词根
class Solution:
def replaceWords(self, dictionary: List[str], sentence: str) -> str:
trie = Trie()
for root in dictionary:
trie.insert(root)
words = sentence.split()
replaced = []
for w in words:
replaced.append(trie.find_prefix(w))
return " ".join(replaced)435,无重叠区间
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠。
注意 只在一点上接触的区间是 不重叠的 。例如 [1, 2] 和 [2, 3] 是不重叠的。
思路,把所有区间先按照右侧位置来从小到大排列,然后遍历
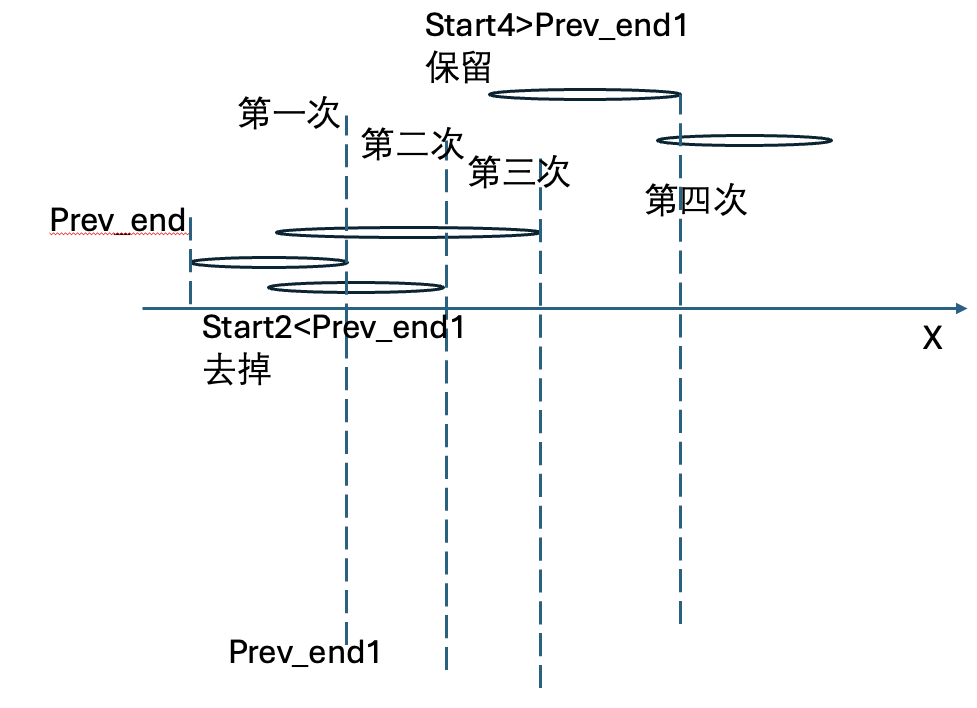

代码实现:
python
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
# 按结束时间排序
intervals.sort(key=lambda x: x[1])
removed = 0
prev_end = float('-inf')
for start, end in intervals:
if start >= prev_end:
# 不重叠,更新 prev_end
prev_end = end
else:
# 重叠,需要移除当前区间
removed += 1
return removed337,打家劫舍(动态规划)
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个"父"房子与之相连。一番侦察之后,聪明的小偷意识到"这个地方的所有房屋的排列类似于一棵二叉树"。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
动态规划问题:
这题就是 House Robber III 。核心思路是 树形 DP + 后序遍历
前置知识:
后序遍历:左->右->当前


先序遍历: 当前->左->右

中序遍历:左->当前 ->右


代码:
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
def dfs(node):
if not node:
return [0, 0] # 维护一个抢和不抢的价值列表
# 后续遍历
left = dfs(node.left)
right = dfs(node.right)
# 分解成根据当前节点的子节点构成的子问题
# rob_cur 当前节点抢,则子节点不能抢
rob_cur = node.val + left[0] + right[0]
# not_rob_cur当前节点不抢,则价值还是子节点的价值,选取子节点较大的那个节点
not_rob_cur = max(left) + max(right)
return [not_rob_cur, rob_cur]
res = dfs(root) # 维护一个抢和不抢的价值列表
return max(res) 1208. 尽可能使字符串相等
中等
给你两个长度相同的字符串,s 和 t。
将 s 中的第 i 个字符变到 t 中的第 i 个字符需要 |s[i] - t[i]| 的开销(开销可能为 0),也就是两个字符的 ASCII 码值的差的绝对值。
用于变更字符串的最大预算是 maxCost。在转化字符串时,总开销应当小于等于该预算,这也意味着字符串的转化可能是不完全的。
如果你可以将 s 的子字符串转化为它在 t 中对应的子字符串,则返回可以转化的最大长度。
如果 s 中没有子字符串可以转化成 t 中对应的子字符串,则返回 0。
思路:这个就是滑动窗口的问题
用ord(获取字母的ascii编码)
python
class Solution:
def equalSubstring(self, s: str, t: str, maxCost: int) -> int:
n = len(s)
l = 0
cost = 0
res = 0
for r in range(n):
cost += abs(ord(s[r]) - ord(t[r])) # ord()把字符转换成它的 ASCII 数值
while cost > maxCost:
cost -= abs(ord(s[l]) - ord(t[l]))
l += 1
# max(res旧的最大长度, r - l + 1 现在新的长度)
res = max(res, r - l + 1)
return res1248. 统计「优美子数组」
中等
给你一个整数数组 nums 和一个整数 k。如果某个连续子数组中恰好有 k 个奇数数字,我们就认为这个子数组是「优美子数组」。
请返回这个数组中 「优美子数组」 的数目。
思路:
这一题不建议用滑动窗口求解!
首先将序列转化为0/1的序列。
然后把k个奇数转化成前缀和为k的问题
通过一个字典来存前缀和为x的信息
从左到右遍历数组
如果当前的prefix减去k(代表一个区间,这个区间的奇数count等于k)
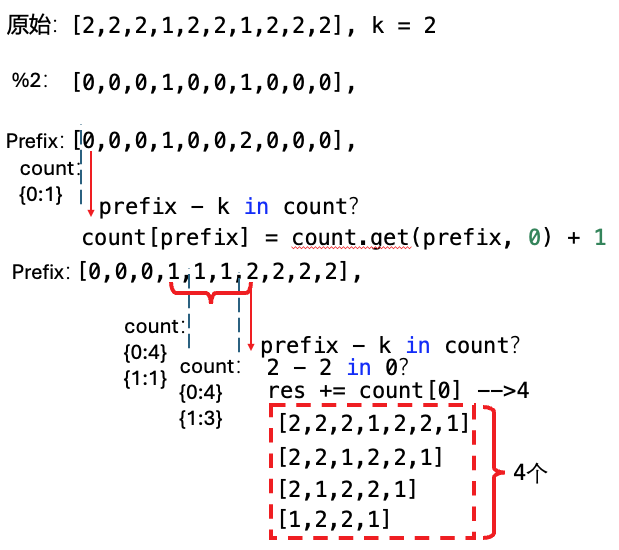
python
class Solution:
def numberOfSubarrays(self, nums, k):
count = {0: 0}
count[0] = 1 # prefix sum 为 0 的初始出现次数
prefix = 0 # prefix 当前的前缀奇数个数(相当于累加奇数变成的 1)
res = 0
# 找到可以组成恰好 k 个奇数的子数组
for x in nums:
prefix += (x % 2) # 奇数变 1 偶数变 0
if prefix - k in count:
res += count[prefix - k]
count[prefix] = count.get(prefix, 0) + 1 # 更新当前前缀出现次数
return res130. 被围绕的区域
中等
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' 组成,捕获 所有 被围绕的区域:
- **连接:**一个单元格与水平或垂直方向上相邻的单元格连接。
- 区域:连接所有
'O'的单元格来形成一个区域。 - 围绕: 如果您可以用
'X'单元格 连接这个区域 ,并且区域中没有任何单元格位于board边缘,则该区域被'X'单元格围绕。
通过 原地 将输入矩阵中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。你不需要返回任何值。
思路:
1,首先将和边缘相连接的O都改成A
2,把剩下所有O都改成X
3,把A都改成O
实现方式,定义dfs函数,搜索四个方向,如果是X或者越界,则直接返回不动,如果是O,则将其改为A
遍历方式,for循环平行遍历顶行和底行,for循环平行遍历第一列和最后一列
代码实现:
python
if not board or not board[0]:
return
m, n = len(board), len(board[0])
def dfs(i, j):
if i < 0 or i >= m or j < 0 or j >= n or board[i][j] != 'O':
return
board[i][j] = 'A'
dfs(i + 1, j)
dfs(i - 1, j)
dfs(i, j + 1)
dfs(i, j - 1)
# 1. 从四条边出发,把所有连通的 O 标为 A
for i in range(m):
dfs(i, 0)
dfs(i, n - 1)
for j in range(n):
dfs(0, j)
dfs(m - 1, j)
# 2. 扫描,将 O 变成 X
# 3. 将 A 变回 O
for i in range(m):
for j in range(n):
if board[i][j] == 'O':
board[i][j] = 'X'
elif board[i][j] == 'A':
board[i][j] = 'O'34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
思路:使用二分查找来分别查找左端点和右端点
分别设置left和right指针在左右两端
pos 默认是-1,如果找到了就标记为target的位置
通过left<=right的循环条件不断缩小区间,用mid和target进行比较来确定下一步怎么缩减
对于左端点:如果mid大于target,则将right缩减到mid-1,否则将left变成mid+1
对右端点同理
代码实现:
python
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
def find_left(nums, target):
left = 0
right = len(nums) - 1
pos = -1
while left <= right:
mid = (left + right) // 2
if nums[mid] >= target:
right = mid - 1
else:
left = mid + 1
if nums[mid] == target:
pos = mid
return pos
def find_right(nums, target):
left, right = 0, len(nums) - 1
pos = -1
while left <= right:
mid = (left + right) // 2
if nums[mid] <= target:
left = mid + 1
else:
right = mid - 1
if nums[mid] == target:
pos = mid
return pos
return [find_left(nums, target), find_right(nums, target)]
437. 路径总和 III
中等
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
思路:
这题需要用到前缀和来算区间
需要维护一个前缀count的字典
使用深度优先搜索,由于是前缀和,每次退出节点时要将prefix count 在当前节点的记录减掉
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
prefix_count = {0:1}
def dfs(node, curr_sum):
if not node:
return 0
curr_sum += node.val
# 有多少条从某个祖先节点到当前节点的路径,它们的值之和刚好等于 targetSum
count = prefix_count.get(curr_sum - targetSum, 0) # 加到prefix_count上
prefix_count[curr_sum] = prefix_count.get(curr_sum, 0) + 1 # 进入该节点
count += dfs(node.left, curr_sum)
count += dfs(node.right, curr_sum)
prefix_count[curr_sum] -= 1 # 往上返回时,要忘记当前节点的前缀和,退出该节点
return count
return dfs(root, 0)