进阶数据结构Splay应用-维护数列

引言

该问题几乎包含了所有的 s p l a y splay splay操作, 如果不了解 s p l a y splay splay可以单击这里

题目-维护数列

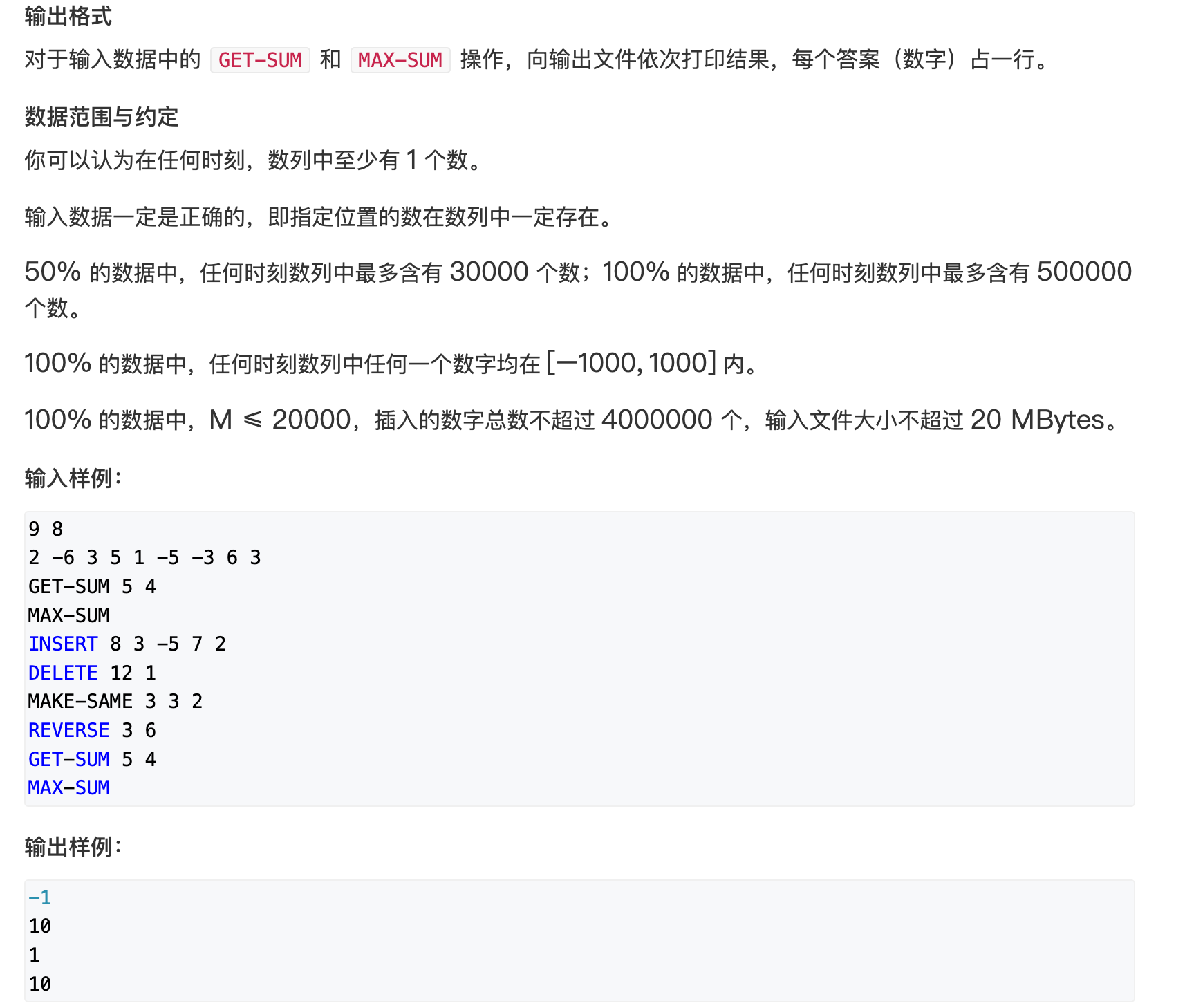
问题分析

因为涉及到区间翻转操作, 线段树无法实现(线段树解决的是区间属性问题)

其实最复杂的操作是求区间的最大
子段和 , 可以考虑 s p l a y splay splay维护的节点信息

最大子段和 m a x v maxv maxv
最长前缀和 l m a x lmax lmax
最长后缀和 r m a x rmax rmax
计算最长前缀和分为两种情况, 跨区间或者在左子区间, 因此还需要区间和 s s s

s p l a y splay splay每个节点表示一个数字 , 多个点构成的树的中序遍历就是希望求的序列 , 因此中序遍历维护的是序列

算法步骤

s p l a y splay splay维护的节点信息

维护最大子段和, m a x v , l m , r m , s u m maxv, lm, rm, sum maxv,lm,rm,sum
节点儿子, 父节点信息 s , p s, p s,p, 当前节点的权值 v v v
是否翻转 r e v rev rev
查询节点的前驱和后继 c n t cnt cnt
整个区间是否变成相同的数 s a m e same same

实现细节

如果一个点有延迟标记, 这个点的权值存储的是执行延迟标记之前的值还是执行延迟标记之后的值需要自己去定义

因为执行 s a m e same same或者 r e v rev rev延迟标记, 会对当前节点的值( m a x v , l m , r m , s u m maxv, lm, rm, sum maxv,lm,rm,sum)产生影响 , 可以定义当前节点的值( m a x v , l m , r m , s u m maxv, lm, rm, sum maxv,lm,rm,sum)是延迟标记操作之后的值

具体的来说

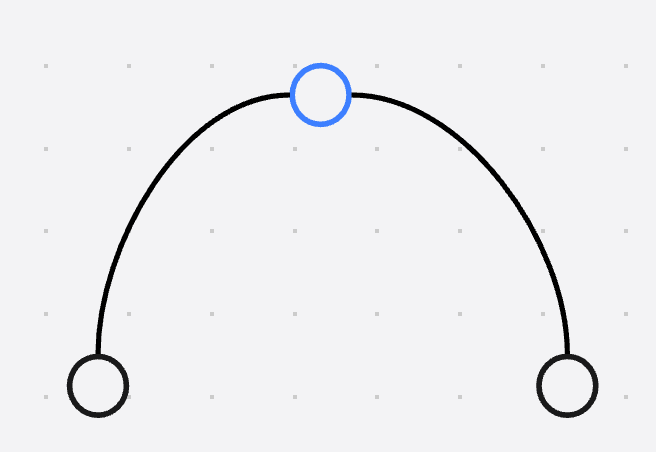
对于当前节点, 如果打上了延迟标记 , 那么将该节点的 m a x v , l m , r m , s u m maxv, lm, rm, sum maxv,lm,rm,sum都计算一遍

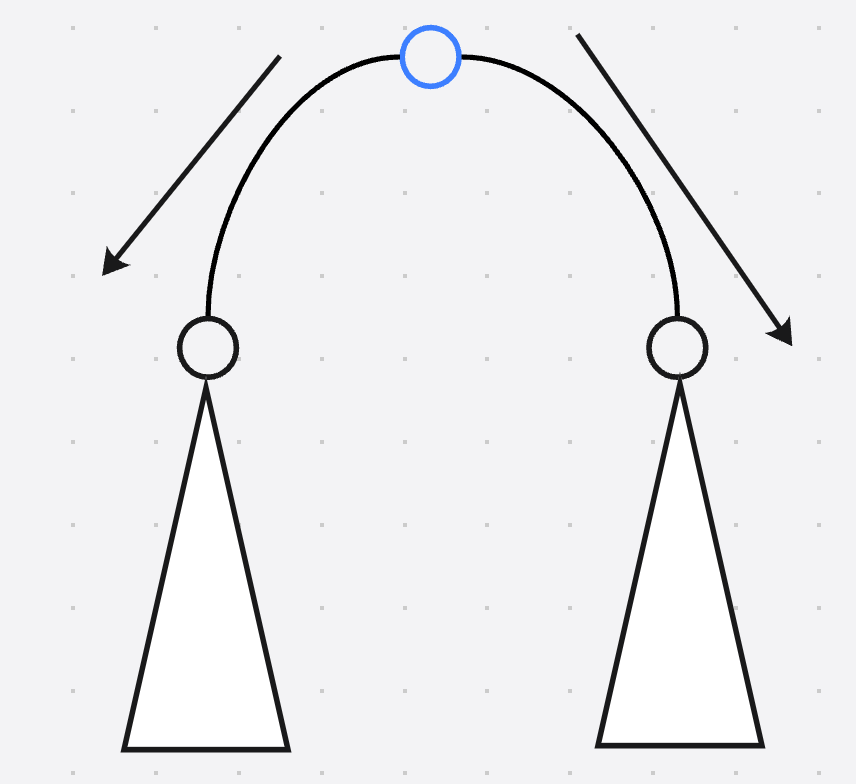
并且在节点执行push down延迟操作的时候, 不仅仅是直接将子节点打上标记, 而且将子节点的 m a x v , l m , r m , s u m maxv, lm, rm, sum maxv,lm,rm,sum计算一遍

在删除过程中 需要进行内存回收优化内存 , 也就是将删除的节点回收到节点池

因此初始化的时候, ms = sum = v, 不能是max(v, 0)

代码实现

注意事项:

计算跨区间的情况 , 需要加当前节点的值 v v v
注意内存池的指针变量不要和父节点变量 p p p重名
因为有哨兵节点的存在, 注意get_k()的参数
延迟标记的处理, 规定如果当前对某个子树打上延迟标记, 对于当前节点立刻生效
题目要求最大子段和最少包含一个点 , 因此初始化ms的时候, 不能设置为 max ⁡ ( v , 0 ) \max(v, 0) max(v,0), 而是没有选择的 设置为 v v v
0 0 0号点是边界哨兵节点 , 因此初始化节点池 的时候, 必须从 1 1 1开始

cpp 复制代码

#include <bits/stdc++.h>

using namespace std;

const int N = 5e5 + 10, INF = 1e9;

int n, m;
struct Node {
    int s[2], p, v;
    int rev, same, cnt;
    int ms, ls, rs, sum;

    // 因为内存回收机制的存在, 必须在此刻重置rev和same的延迟标记
    void init(int _v, int _p) {
        s[0] = s[1] = 0;
        p = _p, v = _v;
        cnt = 1;
        rev = same = 0;
        sum = ms = v;
        ls = rs = max(v, 0);
    }
} tr[N];
// nodes作为节点池, ptr分配节点
int root, nodes[N], ptr;
int w[N];

void pushup(int u) {
    Node &lson = tr[tr[u].s[0]], &rson = tr[tr[u].s[1]];
    tr[u].cnt = lson.cnt + rson.cnt + 1;
    tr[u].sum = lson.sum + rson.sum + tr[u].v;
    tr[u].ls = max(lson.ls, lson.sum + tr[u].v + rson.ls);
    tr[u].rs = max(rson.rs, rson.sum + tr[u].v + lson.rs);
    // 注意需要加当前节点的值
    tr[u].ms = max({lson.ms, rson.ms, lson.rs + tr[u].v + rson.ls});
}

void pushdown(int u) {
    Node &lson = tr[tr[u].s[0]], &rson = tr[tr[u].s[1]];
    if (tr[u].same) {
        tr[u].same = tr[u].rev = 0;
        if (tr[u].s[0]) {
            lson.same = 1;
            lson.v = tr[u].v;
            lson.sum = tr[u].v * lson.cnt;

            if (tr[u].v > 0) lson.ms = lson.ls = lson.rs = lson.sum;
            else {
                lson.ms = tr[u].v;
                lson.ls = lson.rs = 0;
            }
        }
        if (tr[u].s[1]) {
            rson.same = 1;
            rson.v = tr[u].v;
            rson.sum = tr[u].v * rson.cnt;

            if (tr[u].v > 0) rson.ms = rson.ls = rson.rs = rson.sum;
            else {
                rson.ms = tr[u].v;
                rson.ls = rson.rs = 0;
            }
        }
    }
    // 当子树的根被打上标记, 约定翻转, 这里就不需要翻转
    else if (tr[u].rev) {
        tr[u].rev = 0;
        lson.rev ^= 1, rson.rev ^= 1;
        swap(lson.ls, lson.rs), swap(rson.ls, rson.rs);
        swap(lson.s[0], lson.s[1]), swap(rson.s[0], rson.s[1]);
    }
}

void rotate(int x) {
    int y = tr[x].p, z = tr[y].p;
    int k = tr[y].s[1] == x;
    tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
    tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
    tr[x].s[k ^ 1] = y, tr[y].p = x;
    pushup(y), pushup(x);
}

void splay(int x, int k) {
    while (tr[x].p != k) {
        int y = tr[x].p, z = tr[y].p;
        if (z != k) {
            if ((tr[z].s[1] == y) ^ (tr[y].s[1] == x)) rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
    if (!k) root = x;
}

// 将一段序列构建二叉树
int build(int l, int r, int p) {
    int mid = l + r >> 1;
    int u = nodes[ptr--];
    tr[u].init(w[mid], p);
    if (l < mid) tr[u].s[0] = build(l, mid - 1, u);
    if (r > mid) tr[u].s[1] = build(mid + 1, r, u);

    pushup(u);
    return u;
}

int get_k(int k) {
    int u = root;
    while (u) {
        pushdown(u);
        int cnt = tr[tr[u].s[0]].cnt + 1;
        if (cnt > k) u = tr[u].s[0];
        else if (cnt == k) return u;
        else u = tr[u].s[1], k -= cnt;
    }
    return 0;
}

// 内存回收
void release(int u) {
    if (tr[u].s[0]) release(tr[u].s[0]);
    if (tr[u].s[1]) release(tr[u].s[1]);
    nodes[++ptr] = u;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    // 所有点是可用的
    for (int i = 1; i < N; ++i) nodes[++ptr] = i;

    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> w[i];
    // 为了保证数列时刻都有数字以及如果当前节点没有左右儿子节点不会造成影响
    tr[0].ms = w[0] = w[n + 1] = -INF;

    // 原序列初始化为树
    root = build(0, n + 1, 0);

    string op;
    while (m--) {
        cin >> op;
        if (op == "INSERT") {
            int posi, tot;
            cin >> posi >> tot;
            int u = get_k(posi + 1), v = get_k(posi + 2);
            splay(u, 0), splay(v, u);

            for (int i = 0; i < tot; ++i) cin >> w[i];

            tr[v].s[0] = build(0, tot - 1, v);
            pushup(v), pushup(u);
        }
        else if (op == "DELETE") {
            int posi, tot;
            cin >> posi >> tot;

            int u = get_k(posi), v = get_k(tot + posi + 1);
            splay(u, 0), splay(v, u);

            release(tr[v].s[0]);
            tr[v].s[0] = 0;
            pushup(v), pushup(u);
        }
        else if (op == "MAKE-SAME") {
            int posi, tot, c;
            cin >> posi >> tot >> c;

            int u = get_k(posi), v = get_k(tot + posi + 1);
            splay(u, 0), splay(v, u);

            Node &son = tr[tr[v].s[0]];
            son.same = 1;
            son.v = c;
            son.sum = son.cnt * c;

            if (c > 0) son.ms = son.ls = son.rs = son.sum;
            else {
                son.ms = c;
                son.ls = son.rs = 0;
            }
            pushup(v), pushup(u);
        }
        else if (op == "REVERSE") {
            int posi, tot;
            cin >> posi >> tot;

            int u = get_k(posi), v = get_k(tot + posi + 1);
            splay(u, 0), splay(v, u);

            Node &son = tr[tr[v].s[0]];

            son.rev ^= 1;
            swap(son.ls, son.rs);
            swap(son.s[0], son.s[1]);
            pushup(v), pushup(u);
        }
        else if (op == "GET-SUM") {
            int posi, tot;
            cin >> posi >> tot;

            int u = get_k(posi), v = get_k(tot + posi + 1);
            splay(u, 0), splay(v, u);

            cout << tr[tr[v].s[0]].sum << '\n';
            pushup(v), pushup(u);
        }
        else {
            cout << tr[root].ms << '\n';
        }
    }

    return 0;
}