前言
学习机器学习的过程中,我逐渐意识到:
如果只有代码,而没有理论,就很难真正理解模型在做什么
如果只有概念,而缺少一个系统框架,又难以把知识串成体系
《统计学习方法》正好提供了这样一个结构清晰的入口------它把机器学习的核心思想和经典算法用统计学的语言表达出来,帮助我们理解算法背后的原理。

因此,我决定开启这个专栏,用自己的方式整理学习笔记。主要目标是:
- 用更直白的语言梳理书中的概念
- 把知识点整理成便于查阅和复习的形式
- 记录自己的理解和思考过程
这些笔记主要是我个人的学习记录,如果恰好对你也有帮助,那就更好了。希望通过这个过程,能让自己对机器学习的理论基础有更扎实的理解。
第7章------支持向量机(上)
SVM上篇从最基础的线性可分情况出发,讲解硬间隔最大化的原理、函数间隔与几何间隔的概念、对偶优化算法,然后扩展到线性不可分的情况,引入软间隔最大化处理噪声数据,并介绍支持向量的定义和合页损失函数的等价形式。
SVM的核心思想可以这样理解:
首先,SVM本质上是一个分类算法,它的决策函数形式是 f ( x ) = s i g n ( w ⋅ x + b ) f(x) = sign(w \cdot x + b) f(x)=sign(w⋅x+b)
这个公式看起来很眼熟对吧?其实它和Logistic回归有着密切的联系------sign函数部分类似感知机,而 w ⋅ x + b w \cdot x + b w⋅x+b 部分则像Logistic回归中的线性组合。通过概率推导,我们发现当 log P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = w ⋅ x + b \log \frac{P(Y=1|x)}{1-P(Y=1|x)} = w \cdot x + b log1−P(Y=1∣x)P(Y=1∣x)=w⋅x+b 时,分类边界恰好就是超平面 w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0
这就建立了SVM与Logistic回归的理论联系。
但SVM的独特之处在于------它不满足于找到"一个"能分开数据的超平面,而是要找到"最好的那个"。什么叫最好?就是让分类最有把握、最稳定。这就引出了"间隔"的概念。
想象一下那张分类图:圆圈和叉叉分别代表两类数据,中间有无数条超平面都能把它们分开。SVM的聪明之处在于,它定义了一个"分类确信度"指标 ∣ w ⋅ x i + b ∣ ∣ ∣ w ∣ ∣ \frac{|w \cdot x_i + b|}{||w||} ∣∣w∣∣∣w⋅xi+b∣表示点离超平面越远、分类越可靠。同时,用"分类正确性"指标 y i y_i yi 来判断分类对不对。把二者结合起来,就得到了"几何间隔" γ i = y i ( w ⋅ x i + b ) ∣ ∣ w ∣ ∣ \gamma_i = \frac{y_i(w \cdot x_i + b)}{||w||} γi=∣∣w∣∣yi(w⋅xi+b)
SVM的目标很明确:让所有点中 间隔最小的那个点(也就是离超平面最近的点)的间隔尽可能大,即 max w , b min i = 1 , ⋯ , N γ i \max_{w,b} \min_{i=1,\cdots,N} \gamma_i w,bmaxi=1,⋯,Nminγi
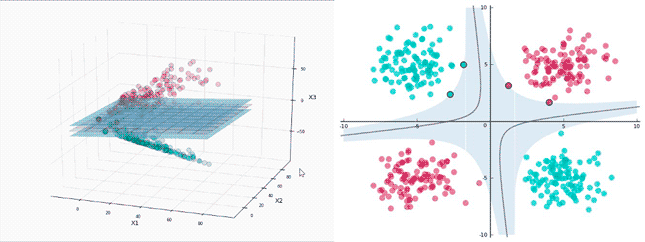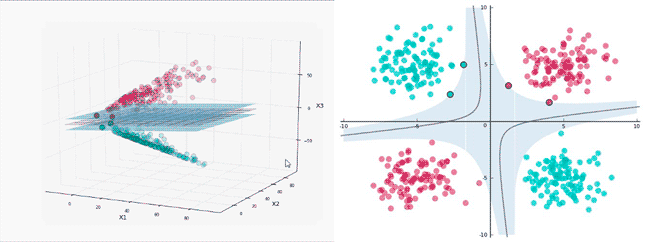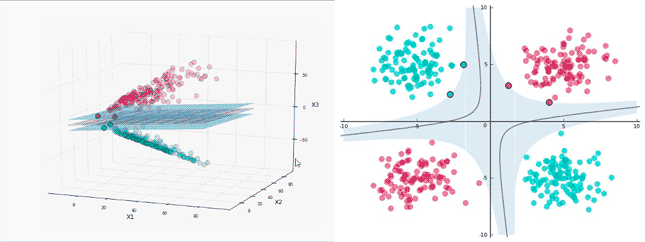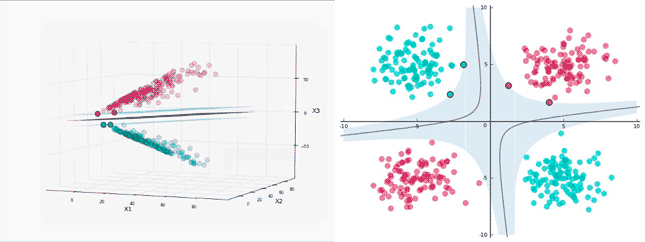
这些离超平面最近的点就是"支持向量",正是因为它们的"支持",我们才能确定唯一的最优超平面。这就是为什么叫"支持向量机"的原因。
7.1 线性可分支持向量机与硬间隔最大化
7.1.1 线性可分支持向量机
线性可分支持向量机解决的是最理想的情况:所有训练数据都能被一个超平面完美分开,没有任何错误。给定训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T = \{(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)},其中 x i ∈ R n x_i \in \mathbb{R}^n xi∈Rn 是特征向量, y i ∈ { + 1 , − 1 } y_i \in \{+1, -1\} yi∈{+1,−1} 是类标记。当数据线性可分时,存在无穷多个超平面都能将两类数据正确分开。
但SVM的目标不是随便找一个分离超平面,而是要找到间隔最大的那个最优超平面。这个最优分离超平面可以写成 w ∗ ⋅ x + b ∗ = 0 w^* \cdot x + b^* = 0 w∗⋅x+b∗=0,对应的分类决策函数是 f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x) = \text{sign}(w^* \cdot x + b^*) f(x)=sign(w∗⋅x+b∗)
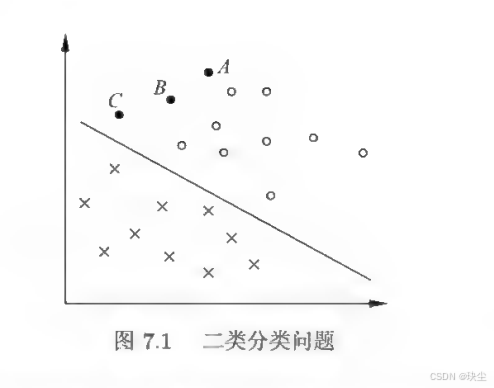
在所有能正确分类的超平面中,SVM选择的是让两类数据之间的"安全距离"最大的那一个,这样的分类器更稳定、泛化能力更强。这就是线性可分支持向量机的核心思想------通过间隔最大化来寻找最优分离超平面。
7.1.2 函数间隔和几何间隔
为了量化"点离超平面有多远"这个直观概念,我们需要定义两种间隔。首先是函数间隔,它是最直接的度量方式。对于超平面 ( w , b ) (w, b) (w,b) 和样本点 ( x i , y i ) (x_i, y_i) (xi,yi),函数间隔定义为 γ ^ i = y i ( w ⋅ x i + b ) \hat{\gamma}_i = y_i(w \cdot x_i + b) γ^i=yi(w⋅xi+b)
这个定义很巧妙:如果分类正确, w ⋅ x i + b w \cdot x_i + b w⋅xi+b 和 y i y_i yi 同号,函数间隔就是正值;而且这个值越大,说明分类越确信。整个训练集的函数间隔则取所有样本点中最小的那个,即 γ ^ = min i = 1 , ⋯ , N γ ^ i \hat{\gamma} = \min_{i=1,\cdots,N} \hat{\gamma}_i γ^=i=1,⋯,Nminγ^i
但函数间隔有个问题:如果我们把 w w w 和 b b b 同时扩大2倍,超平面其实没有变化,但函数间隔却变成了原来的2倍。为了消除这种不确定性,我们对法向量 w w w 加上约束,要求 ∣ ∣ w ∣ ∣ = 1 ||w|| = 1 ∣∣w∣∣=1,这样就得到了几何间隔。几何间隔的定义是 γ i = y i ( w ∣ ∣ w ∣ ∣ ⋅ x i + b ∣ ∣ w ∣ ∣ ) \gamma_i = y_i\left(\frac{w}{||w||} \cdot x_i + \frac{b}{||w||}\right) γi=yi(∣∣w∣∣w⋅xi+∣∣w∣∣b),它表示的是样本点到超平面的真实带符号距离。几何间隔和函数间隔的关系很简单: γ i = γ ^ i ∣ ∣ w ∣ ∣ \gamma_i = \frac{\hat{\gamma}_i}{||w||} γi=∣∣w∣∣γ^i,也就是说,几何间隔是归一化后的函数间隔,它不会因为参数的成比例缩放而改变,是一个稳定的度量。
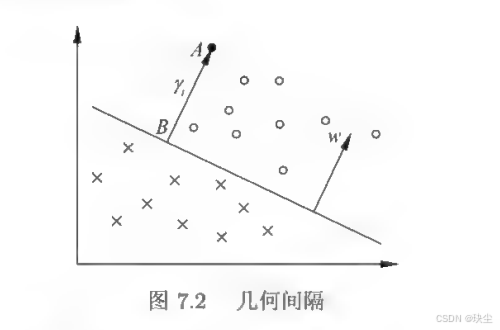
7.1.3 间隔最大化
支持向量机的目标不仅是"把两类样本分开",而是要 分得越稳越好 。
所谓"稳",可以理解成:我们希望两类样本和分界超平面之间留出一段 安全距离(间隔) 。
这样即便出现轻微噪声或新样本分布和训练数据不完全一致,分类器也不会轻易出错。
要做到这一点,我们希望:
每个样本距离超平面至少要有 γ \gamma γ 这么大。
进一步,根据几何间隔与函数间隔的关系,我们把问题改写成一个更容易处理的形式:
最大化 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1就等价于让间隔最大。
为了让优化问题更简洁,我们利用一个重要的性质:
把 w w w 和 b b b 同时按比例放大,超平面并不会改变。
所以我们可以把函数间隔 固定为 1。这样问题就变成了:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min_{w,b} \frac12 ||w||^2 w,bmin21∣∣w∣∣2
subject to y i ( w ⋅ x i + b ) ≥ 1 \text{subject to } y_i(w\cdot x_i + b)\ge 1 subject to yi(w⋅xi+b)≥1
这就是经典的 硬间隔最大化 SVM。
求解后,我们得到最优的分离超平面:
w ∗ ⋅ x + b ∗ = 0 w^*\cdot x + b^* = 0 w∗⋅x+b∗=0
分类决策函数就是:
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x) = \text{sign}(w^*\cdot x + b^*) f(x)=sign(w∗⋅x+b∗)
支持向量:谁决定了最终的超平面?
在所有训练样本中,并不是每个都会影响最终结果。
只有那些恰好压在间隔边界上的点 ,也就是满足: y i ( w ∗ ⋅ x i + b ∗ ) = 1 y_i(w^*\cdot x_i + b^*) = 1 yi(w∗⋅xi+b∗)=1 的样本,会对结果起作用。
这些点叫做 支持向量。
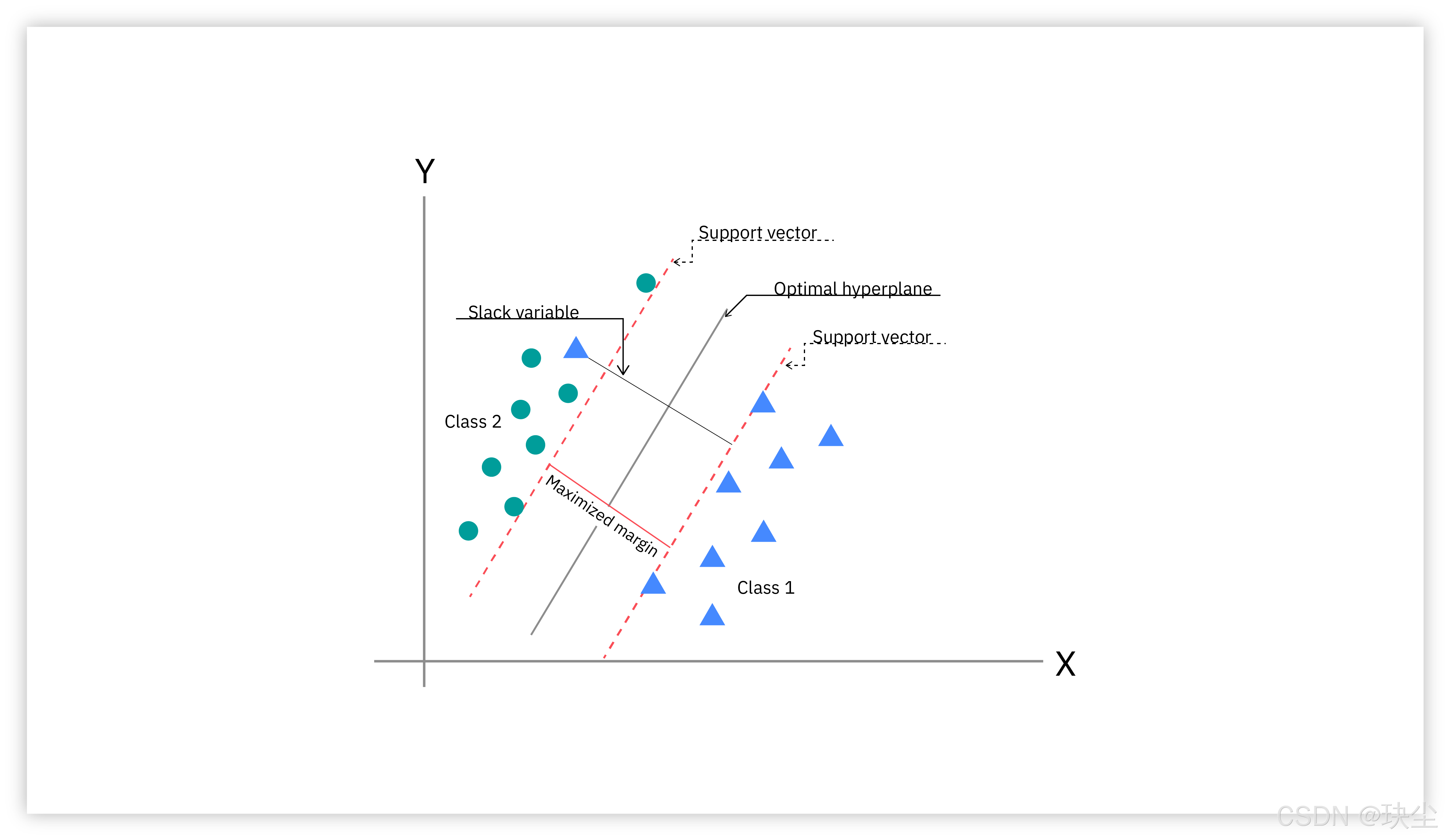
它们分别位于两侧的两个超平面上:
- 正类支持向量在: w ⋅ x + b = 1 w\cdot x + b = 1 w⋅x+b=1
- 负类支持向量在: w ⋅ x + b = − 1 w\cdot x + b = -1 w⋅x+b=−1
这两个超平面围出的带状区域就是"安全带",宽度为:
2 ∣ ∣ w ∣ ∣ \frac{2}{||w||} ∣∣w∣∣2
神奇的是:
只要这些支持向量不动,其他点随便移动都不会改变最终的超平面。
SVM 之所以叫"支持向量机",就是因为 分类结果完全由少数几个支持向量决定。
7.1.4 学习的对偶算法
为了更高效地求解 SVM,并为后面处理非线性问题铺路,我们需要把原问题转成它的 对偶问题。这个转换属于拉格朗日优化的内容,但这里只讲核心思想,不深入数学细节。
1、为什么要搞对偶?
两个原因:
① 对偶问题更容易求解。
原始变量是 w w w 和 b b b,维度高、约束多。对偶问题只涉及一组系数 α i \alpha_i αi,并且配上高效算法更容易求。
② 对偶形式只依赖样本内积 x i ⋅ x j x_i\cdot x_j xi⋅xj
这为后面"核函数"替代内积、从而做非线性分类,打下理论基础。
2、先写拉格朗日函数
对每个约束 y i ( w ⋅ x i + b ) ≥ 1 y_i(w\cdot x_i+b)\ge 1 yi(w⋅xi+b)≥1,
我们引入一个拉格朗日乘子 α i ≥ 0 \alpha_i\ge 0 αi≥0。
构造出拉格朗日函数:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ α i y i ( w ⋅ x i + b ) + ∑ α i L(w,b,\alpha) = \frac12 ||w||^2 - \sum \alpha_i y_i(w\cdot x_i + b) + \sum \alpha_i L(w,b,α)=21∣∣w∣∣2−∑αiyi(w⋅xi+b)+∑αi
核心想法是:
找到既满足约束、又能使目标函数最小的 w , b w,b w,b,同时让 α \alpha α 尽可能大。
3、通过对 w , b w, b w,b 求偏导,可以得到两条重要关系:
w = ∑ α i y i x i w = \sum \alpha_i y_i x_i w=∑αiyixi
∑ α i y i = 0 \sum \alpha_i y_i = 0 ∑αiyi=0
这两条非常关键。
第一条说明:最终的权重向量 w w w 是由训练样本线性组合得到的,而系数就是 α i y i \alpha_i y_i αiyi。
第二条是对偶问题的一个约束。
4、消去 w w w 和 b b b 后,就得到对偶问题
对偶问题是一个关于 α i \alpha_i αi 的优化:
min α 1 2 ∑ i , j α i α j y i y j ( x i ⋅ x j ) − ∑ i α i \min_\alpha \frac12 \sum_{i,j} \alpha_i\alpha_j y_i y_j(x_i\cdot x_j)- \sum_i \alpha_i αmin21i,j∑αiαjyiyj(xi⋅xj)−i∑αi
约束:
∑ i α i y i = 0 , α i ≥ 0 \sum_i \alpha_i y_i = 0,\quad \alpha_i \ge 0 i∑αiyi=0,αi≥0
这就是 线性可分 SVM 的对偶形式。
5、KKT 条件告诉我们:支持向量 ↔ α i > 0 \alpha_i > 0 αi>0
KKT 条件给出一个非常直观的结论:
α i ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 ) = 0 \alpha_i(y_i(w^*\cdot x_i + b^*) - 1) = 0 αi(yi(w∗⋅xi+b∗)−1)=0
因此:
-
若样本不是支持向量,则 α i = 0 \alpha_i = 0 αi=0
-
若样本恰好压在间隔边界上,则 α i > 0 \alpha_i > 0 αi>0
6、最终的模型长这样
权重向量:
w ∗ = ∑ α i ∗ y i x i w^* = \sum \alpha_i^* y_i x_i w∗=∑αi∗yixi
偏置可以用任意一个支持向量求:
b ∗ = y j − ∑ i α i ∗ y i ( x i ⋅ x j ) b^* = y_j - \sum_i \alpha_i^*y_i(x_i\cdot x_j) b∗=yj−i∑αi∗yi(xi⋅xj)
最终分类函数:
f ( x ) = sign ( ∑ i α i ∗ y i ( x ⋅ x i ) + b ∗ ) f(x) = \text{sign}\left(\sum_i \alpha_i^* y_i (x\cdot x_i) + b^*\right) f(x)=sign(i∑αi∗yi(x⋅xi)+b∗)
对于线性可分问题,上述线性可分支持向量机的学习(硬问隔最大化)算法是完美的。但是,训练数据集线性可分是理想的情形。在现实问题中,训练数据集往往是线性不可分的,即在样本中出现噪声或特异点。此时,有更一般的学习算法。
7.2 线性支持向量机与软间隔最大化
7.2.1 线性支持向量机
在现实中,数据往往不是整整齐齐地分成两类。它们会混在一起,有些点可能跑到对方阵营附近,这种情况就叫做"线性不可分"。既然完全分开做不到,我们只能退而求其次:允许一些点分错,但整体的间隔要尽可能大。
这就是软间隔的思想。
在硬间隔 SVM 中,要求所有样本必须满足:
y i ( w ⋅ x i + b ) ≥ 1. y_i(w\cdot x_i+b)\ge 1. yi(w⋅xi+b)≥1.
但如果数据本来就无法完全隔开,这个条件根本做不到。
于是我们给每个样本点加一个"违规量":
ξ i ≥ 0. \xi_i\ge 0. ξi≥0.
它表示:
- ξ = 0:完全满足要求
- 0 < ξ < 1:点在间隔带里面了,但没越界
- ξ > 1:这个点甚至被分错类了
所以新的条件变成:
y i ( w ⋅ x i + b ) ≥ 1 − ξ i . y_i(w\cdot x_i+b)\ge 1-\xi_i. yi(w⋅xi+b)≥1−ξi.
允许违规可以,但不能太随便。于是我们在目标函数里加了"处罚":
1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ ξ i . \frac12||w||^2 + C\sum\xi_i. 21∣∣w∣∣2+C∑ξi.
这里有两个部分:
- 第一项:让间隔尽可能大
- 第二项:让违规(误分类)尽可能少
- C:控制这两者的平衡
简单理解:
| C 大 | C 小 |
|---|---|
| 惩罚更重,不许分错,模型更严格 | 惩罚变轻,可以容忍错误,模型更宽松 |
最终,我们要做的事情是:
min 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ ξ i \min\frac12||w||^2 + C\sum\xi_i min21∣∣w∣∣2+C∑ξi
满足:
- 样本可以软性满足分类条件 y i ( w ⋅ x i + b ) ≥ 1 − ξ i y_i(w\cdot x_i+b)\ge 1-\xi_i yi(w⋅xi+b)≥1−ξi
- 不能出现负的松弛量 ξ i ≥ 0 \xi_i\ge 0 ξi≥0
这是一个标准的凸二次规划问题,保证有唯一解。
求出来的解,就是 线性支持向量机。
7.2.2 学习的对偶算法
上面的问题可以直接求解,但在支持向量机中,更常用的方法是求 对偶问题。为什么?
- 对偶问题更容易处理约束
- 更容易扩展到核函数
- 训练中只用到样本之间的内积(非常重要)
所以我们需要把原始问题"翻译"成它的对偶形式。
1. 建立拉格朗日函数:把约束揉进去
为了把约束问题变成一个"无约束"的形式,我们加上拉格朗日乘子:
- α:用来约束分类条件
- μ:用来约束 ξ ≥ 0
于是得到一个大公式(不必强背):
L ( w , b , ξ , α , μ ) = ⋯ L(w,b,\xi,\alpha,\mu)=\cdots L(w,b,ξ,α,μ)=⋯
意义不用深究,只要知道:它是用来把约束塞进目标函数中的数学工具。
2. 对 w、b、ξ 求偏导并令其为零
这步的本质是:把不需要的变量消掉,只留下 α。
求导后可以得到三个重要结论:
- w = ∑ α i y i x i w = \sum\alpha_i y_i x_i w=∑αiyixi ⟶ 最终的 w 是由支持向量组合出来的
- ∑ α i y i = 0 \sum\alpha_i y_i = 0 ∑αiyi=0 ⟶ 保证分界线的方向正确
- 0 ≤ α i ≤ C 0\le\alpha_i\le C 0≤αi≤C ⟶ 有了 C 的上界,控制误分类
3. 得到真正要解的对偶问题
把上面的关系代回去,得到最终的二次规划:
max α − 1 2 ∑ i , j α i α j y i y j ( x i ⋅ x j ) + ∑ α i \max_{\alpha}-\frac12\sum_{i,j}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum\alpha_i αmax−21i,j∑αiαjyiyj(xi⋅xj)+∑αi
约束:
- ∑ α i y i = 0 \sum\alpha_i y_i=0 ∑αiyi=0
- 0 ≤ α i ≤ C 0\le\alpha_i\le C 0≤αi≤C
这就是对偶问题。训练 SVM,就是求 α 的过程。
4. 求出 w 和 b
α 求出来后:
w ∗ = ∑ α i ∗ y i x i w^*=\sum\alpha_i^*y_ix_i w∗=∑αi∗yixi
找一个满足
0 < α j ∗ < C 0<\alpha_j^*<C 0<αj∗<C
的点(它一定是支持向量),用它求 b:
b ∗ = y j − ∑ y i α i ∗ ( x i ⋅ x j ) b^*=y_j-\sum y_i\alpha_i^*(x_i\cdot x_j) b∗=yj−∑yiαi∗(xi⋅xj)
5. 最终的分类器
f ( x ) = sign ( ∑ α i ∗ y i ( x ⋅ x i ) + b ∗ ) f(x)=\text{sign}\left(\sum \alpha_i^* y_i(x\cdot x_i)+b^*\right) f(x)=sign(∑αi∗yi(x⋅xi)+b∗)
你会发现:
- 所有 α i α_i αi 为 0 的点都没用
- 只有支持向量 α i > 0 α_i > 0 αi>0 才会参与分类
- 这就是"支持向量机"的本质含义
7.2.3 支持向量
在线性不可分的情况下,将对偶问题的解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) \alpha^* = (\alpha_1^*, \alpha_2^*, \cdots, \alpha_N^*) α∗=(α1∗,α2∗,⋯,αN∗) 中对应于 α i ∗ > 0 \alpha_i^* > 0 αi∗>0 的样本点 ( x i , y i ) (x_i, y_i) (xi,yi) 的实例 x i x_i xi 称为支持向量(软间隔的支持向量)。如图所示,这时的支持向量要比线性可分时的情况复杂一些。图中,分离超平面由实线表示,间隔边界由虚线表示,正例点由"○"表示,负例点由"×"表示,图中还标出了实例 x i x_i xi 到间隔边界的距离 ξ i ∥ w ∥ \frac{\xi_i}{\|w\|} ∥w∥ξi。
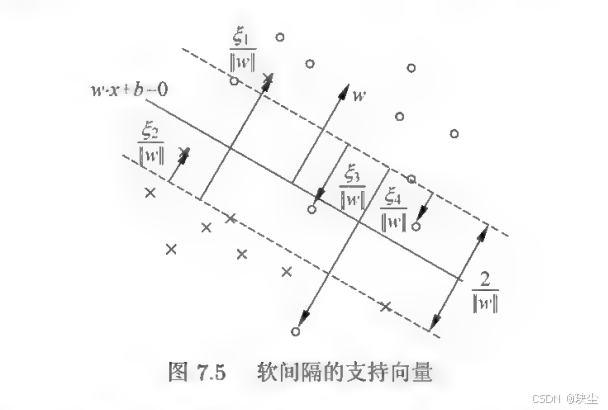
软间隔的支持向量 x i x_i xi 或者在间隔边界上,或者在间隔边界与分离超平面之间,或者在分离超平面误分一侧。具体而言:
- 若 α i ∗ < C \alpha_i^* < C αi∗<C,则 ξ i = 0 \xi_i = 0 ξi=0,支持向量 x i x_i xi 恰好落在间隔边界上
- 若 α i ∗ = C \alpha_i^* = C αi∗=C, 0 < ξ i < 1 0 < \xi_i < 1 0<ξi<1,则分类正确, x i x_i xi 在间隔边界与分离超平面之间
- 若 α i ∗ = C \alpha_i^* = C αi∗=C, ξ i = 1 \xi_i = 1 ξi=1,则 x i x_i xi 在分离超平面上
- 若 α i ∗ = C \alpha_i^* = C αi∗=C, ξ i > 1 \xi_i > 1 ξi>1,则 x i x_i xi 位于分离超平面误分一侧
7.2.4 合页损失函数
在线性支持向量机中,我们最终学到的是一个分离超平面 w ∗ ⋅ x + b ∗ = 0 w^* \cdot x + b^* = 0 w∗⋅x+b∗=0,以及根据它来分类的决策函数 f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\text{sign}(w^* \cdot x + b^*) f(x)=sign(w∗⋅x+b∗)。在线性不可分的情况下,SVM 通过软间隔最大化来学习模型,也就是允许少量样本不满足严格的间隔要求。虽然原来的推导是通过带约束的二次规划完成的,但 SVM 还可以换一种更直观的方式理解:它相当于在最小化一种叫做"合页损失"的函数。
更具体地说,线性 SVM 会优化下面这个目标:
∑ i = 1 N [ 1 − y i ( w ⋅ x i + b ) ] ∗ + + λ ∣ w ∣ 2 \sum_{i=1}^{N}[1 - y_i(w \cdot x_i + b)]*+ + \lambda|w|^2 i=1∑N[1−yi(w⋅xi+b)]∗++λ∣w∣2
其中第一部分是对训练数据的损失,采用的是合页损失
L ( y ( w ⋅ x + b ) ) = [ 1 − y ( w ⋅ x + b ) ] ∗ + L(y(w\cdot x+b))=[1-y(w\cdot x+b)]*+ L(y(w⋅x+b))=[1−y(w⋅x+b)]∗+
而符号 [ z ] + [z]_+ [z]+ 的意思就是"如果 z 是正的就取 z,否则就取 0"。这意味着:如果某个样本不仅被分对了,而且离超平面至少有 1 的"安全距离",那么它的损失就是 0;但如果它离超平面太近,或者干脆被分错了,那么损失就会变成 1 − y ( w ⋅ x + b ) 1 - y(w\cdot x+b) 1−y(w⋅x+b),距离越"不安全",损失越大。所以合页损失的逻辑是:不仅要分类正确,还要"分得舒服",确信度要足够高才算真正没有损失。
与这种损失形式对应的,是原来软间隔最大化的那套数学推导。原始问题是最小化
1 2 ∣ w ∣ 2 + C ∑ i = 1 N ξ i \frac{1}{2}|w|^2 + C\sum_{i=1}^{N}\xi_i 21∣w∣2+Ci=1∑Nξi
同时满足
y i ( w ⋅ x i + b ) ≥ 1 − ξ i , ξ i ≥ 0 。 y_i(w\cdot x_i+b)\ge 1-\xi_i,\quad \xi_i\ge 0。 yi(w⋅xi+b)≥1−ξi,ξi≥0。
定理告诉我们,这个带松弛变量、带约束的优化问题,其实和"合页损失 + 正则化项"的无约束问题完全等价。换句话说,只要最小化合页损失,我们就间接完成了软间隔最大化,得到的模型和之前一样。
为了更好理解合页损失,可以看看它的形状。横轴是样本的函数间隔 y ( w ⋅ x + b ) y(w\cdot x+b) y(w⋅x+b),纵轴是损失值。当间隔大于 1 时,损失是 0;小于 1 时,损失线性增大。图像看起来就像一个折起来的合页,因此得名"合页损失"。另外,图中还画了真正的分类损失------0-1 损失。虽然 0-1 损失意义很直接:分错了就记 1 分损失,分对了记 0 分,但它太不光滑,几乎无法直接优化。合页损失刚好是它的上界,形状更规整、数学性质更好,所以 SVM 实际上是在优化一个可计算的"替代品"。
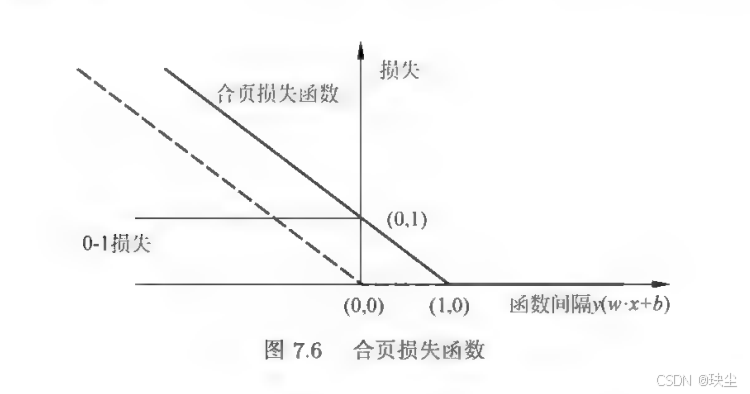
图中虚线显示的是一条感知机的损失线,表达式是 [ − y ( w ⋅ x + b ) ] + [-y(w\cdot x+b)]_+ [−y(w⋅x+b)]+。和合页损失相比,感知机"要求更低":只要分对了就没损失,不管距离近还是远。但合页损失不一样,它希望分类不仅正确,而且要有足够大的间隔,所以会推动分类面变得更"安全"。这也是 SVM 比感知机更稳定、更有泛化能力的原因之一。