一公式
计算平面直角坐标系中两个点的距离,核心是基于欧几里得距离公式:、
对于点 P1(x1, y1) 和 P2(x2, y2),距离 d = √[(x2-x1)² + (y2-y1)²]
二代码化
python
#Point1 x, y坐标
x1 = 100
y1 = 200
#Point2 x, y坐标
x2 = 300
y2 =200
distance = (pow(x2-x1,2) + pow(y2-y1,2)) **0.5 Pow还是用**
python
#使用**
distance1 = (((x2-x1) **2) + ((y2-y1**2))) **0.5
#使用pow
distance2 = pow(pow(x2-x1,2) + pow(y2-y1,2),0.5)
print(distance1)
print(distance2)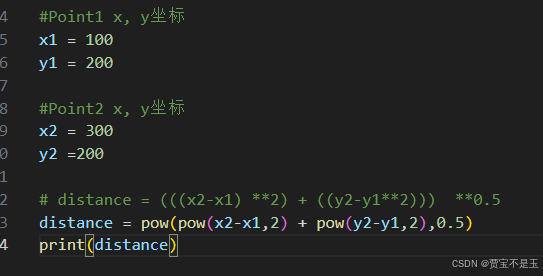
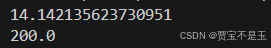
为什么出错,我明白了就是括号中来回增加,弄乱了
更正后的效果
python
#Point1 x, y坐标
x1 = 100
y1 = 200
#Point2 x, y坐标
x2 = 300
y2 =200
distance1 = ((x2-x1) **2 + (y2-y1)**2) ** 0.5
distance2 = pow((pow(x2-x1,2) + pow(y2-y1,2)),0.5)
print(distance1)
print(distance2)如何规避这个问题呢?
分别赋值
python
# 把两个算式分别变量赋值
a = pow(x2-x1,2)
b = pow(y2-y1,2)
c = pow(a+b,0.5)
print(f"点1 x:{x1}, y:{y1}, 点2 x:{x2}, y:{y2}")
print(f"采用分别赋值的办法,最后结果为{c}")