SLAM中的非线性优-3D图优化之相对位姿Between Factor右扰动（八）

前两节已经详细讲解了左扰动的推导方式，本节来看下右扰动的推导，另外右扰动的方式，也被GTSAM中Between Factor所采用，待理论推导后，再来展示相关代码部分，接下来继续沿用之前的图来说明问题

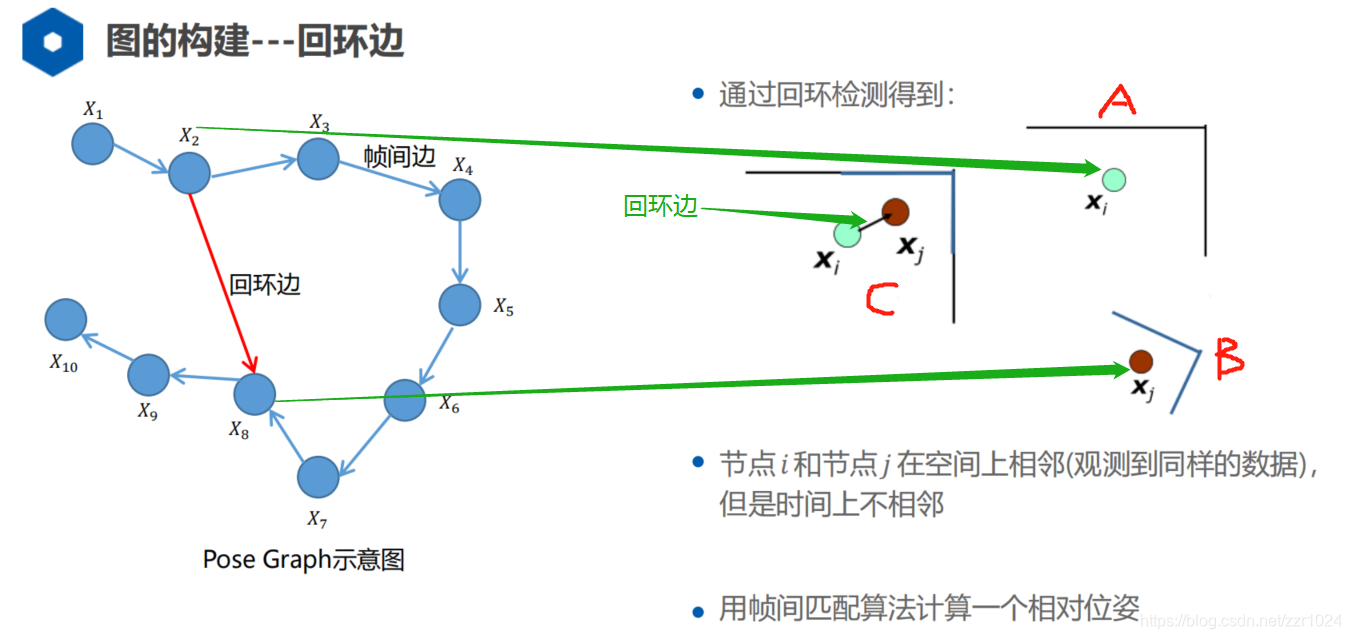
所谓右扰动，即扰动项放在待求量的右边，上节基础部分已展示，这里不再重复。

一. 问题描述

1.1 对i时刻位姿施加右扰动

1.2 对j时刻位姿施加右扰动

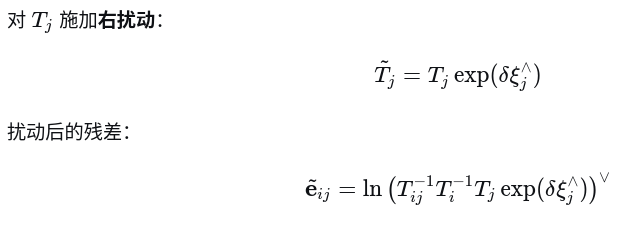
二. 雅可比推导

3.1 先对i时刻求导

(1) 用指数表示原始残差

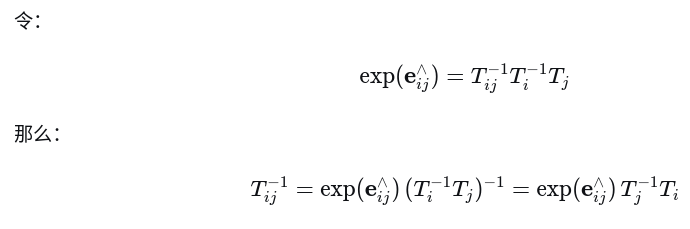(2) 代入扰动后的残差

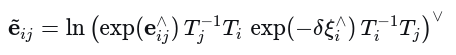
(3) 利用伴随性质

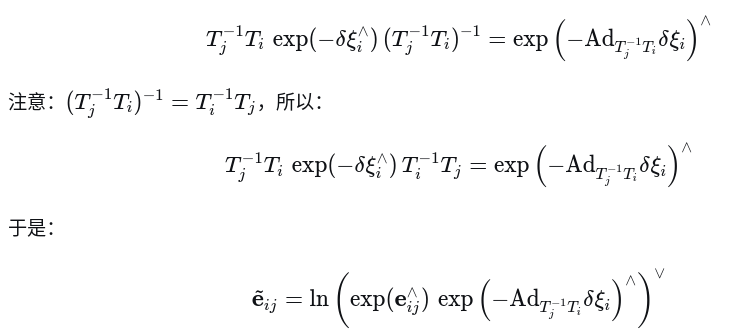
(4) 应用 BCH 公式

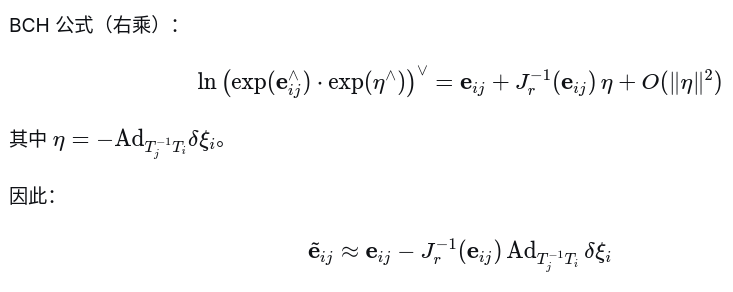
(5) 得到雅可比

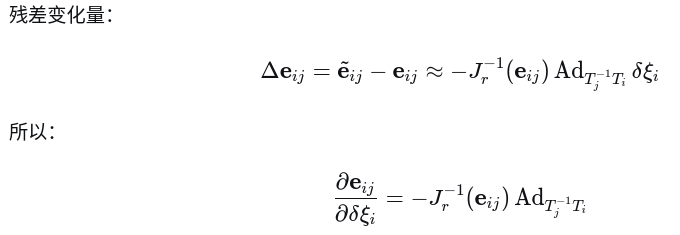
(6) 最终结果（右扰动）

注意：在（六）中介绍过，右雅可比可近似为单位阵，因此i时刻雅可比可简化为如下

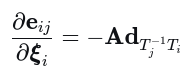
(7) 与左扰动对比

(8) 验证零空间性质

3.2 再对j时刻求导

(1) 用指数表示原始残差

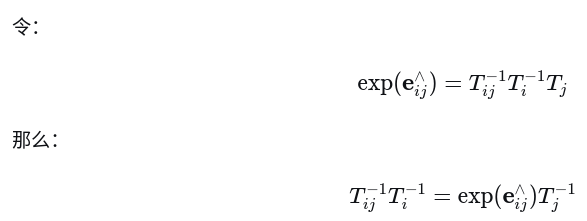
(2) 代入扰动后的残差

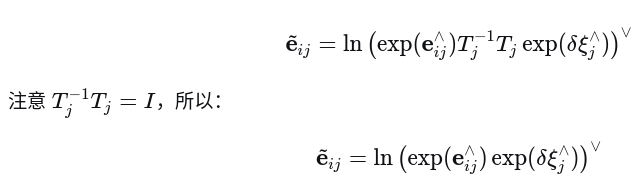
(3) 应用 BCH 公式

(4) 得到雅可比

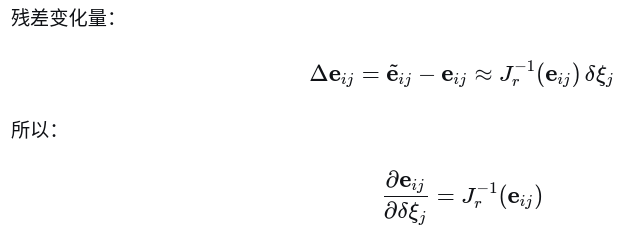
(5) 最终结果（右扰动）

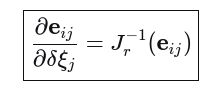
同样，右雅可的逆可近似为单位阵，因此

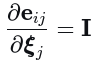
(6) 与左扰动对比

(7) 验证零空间性质

三. 代码展示

此处代码以GTSAM-4.2.0版本为例，误差模型跟雅可比如下所示

复制代码

    /// evaluate error, returns vector of errors size of tangent space
    Vector evaluateError(const T& p1, const T& p2, boost::optional<Matrix&> H1 =
      boost::none, boost::optional<Matrix&> H2 = boost::none) const override {
      T hx = traits<T>::Between(p1, p2, H1, H2); // h(x)
      // manifold equivalent of h(x)-z -> log(z,h(x))
#ifdef GTSAM_SLOW_BUT_CORRECT_BETWEENFACTOR
      typename traits<T>::ChartJacobian::Jacobian Hlocal;
      Vector rval = traits<T>::Local(measured_, hx, boost::none, (H1 || H2) ? &Hlocal : 0);
      if (H1) *H1 = Hlocal * (*H1);
      if (H2) *H2 = Hlocal * (*H2);
      return rval;
#else
      return traits<T>::Local(measured_, hx);
#endif
    }

这里的

复制代码

T hx = traits<T>::Between(p1, p2, H1, H2); // h(x) 即为雅可比矩阵

内部实现

复制代码

  Class between(const Class& g, ChartJacobian H1,
      ChartJacobian H2 = boost::none) const {
    Class result = derived().inverse() * g;
    if (H1) *H1 = - result.inverse().AdjointMap();
    if (H2) *H2 = Eigen::Matrix<double, N, N>::Identity();
    return result;
  }

上述中H1即为推导中的i时刻雅可比；H2为j时刻雅可比，与推导完全一致

返回值

复制代码

return traits<T>::Local(measured_, hx);

Vector6 Pose3::ChartAtOrigin::Local(const Pose3& pose, ChartJacobian Hpose) {
#ifdef GTSAM_POSE3_EXPMAP
  return Logmap(pose, Hpose);
#else
  Matrix3 DR;
  Vector3 omega = Rot3::LocalCoordinates(pose.rotation(), Hpose ? &DR : 0);
  if (Hpose) {
    *Hpose = I_6x6;
    Hpose->topLeftCorner<3, 3>() = DR;
  }
  Vector6 xi;
  xi << omega, pose.translation();
  return xi;
#endif
}

即为残差项

复制代码

#ifdef GTSAM_SLOW_BUT_CORRECT_BETWEENFACTOR
      typename traits<T>::ChartJacobian::Jacobian Hlocal;
      Vector rval = traits<T>::Local(measured_, hx, boost::none, (H1 || H2) ? &Hlocal : 0);
      if (H1) *H1 = Hlocal * (*H1);
      if (H2) *H2 = Hlocal * (*H2);
      return rval;
#else
        
#endif

这里放下一节再讲解；

总结：

本节详细推导了右扰动下的残差跟雅可比，并展示了gtsam库中的实现，与推导一摸一样，足以证明理论的正确性，下一节将详细对比左右扰动下雅可比代码实现