CCF-NOI2025第二试题目与解析（第二题、集合（set））

汉克老师2025-12-12 16:04

一、先看原题：

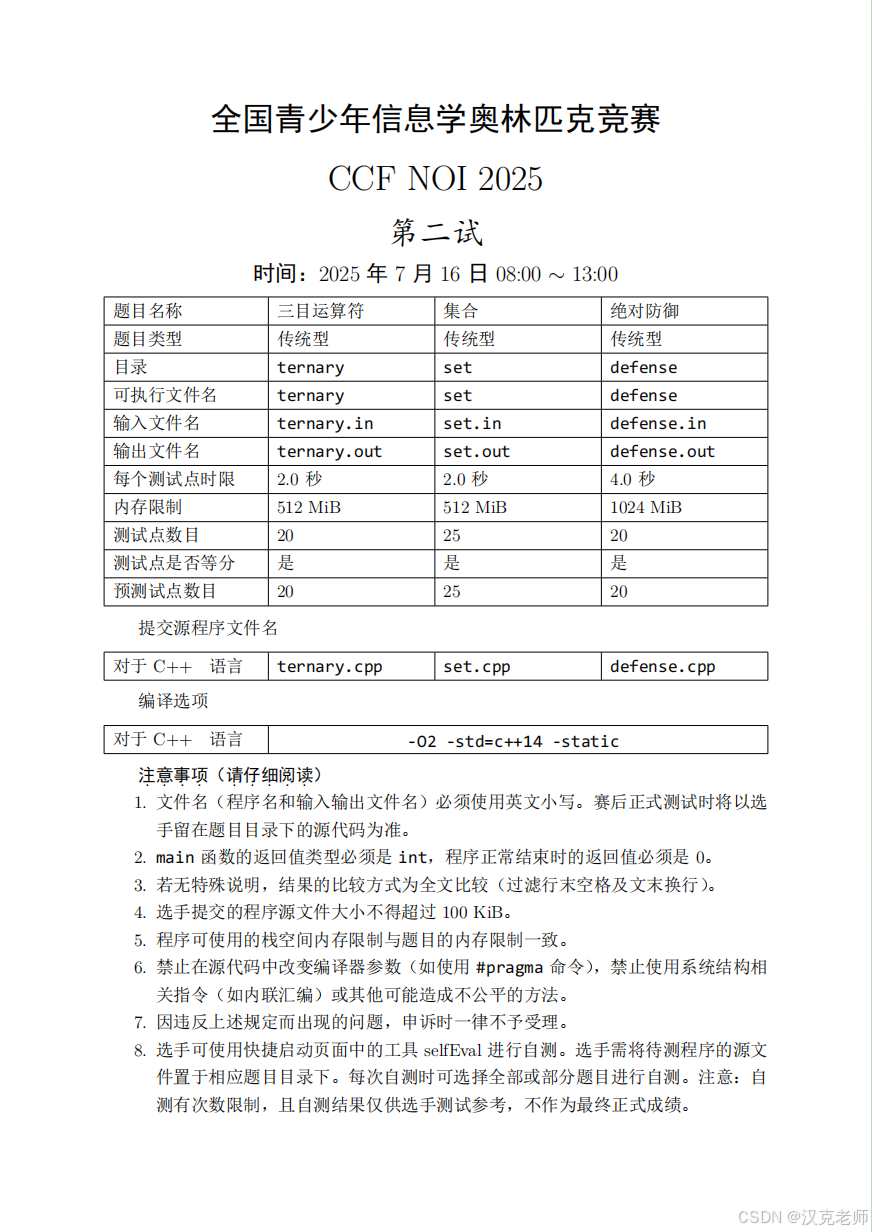
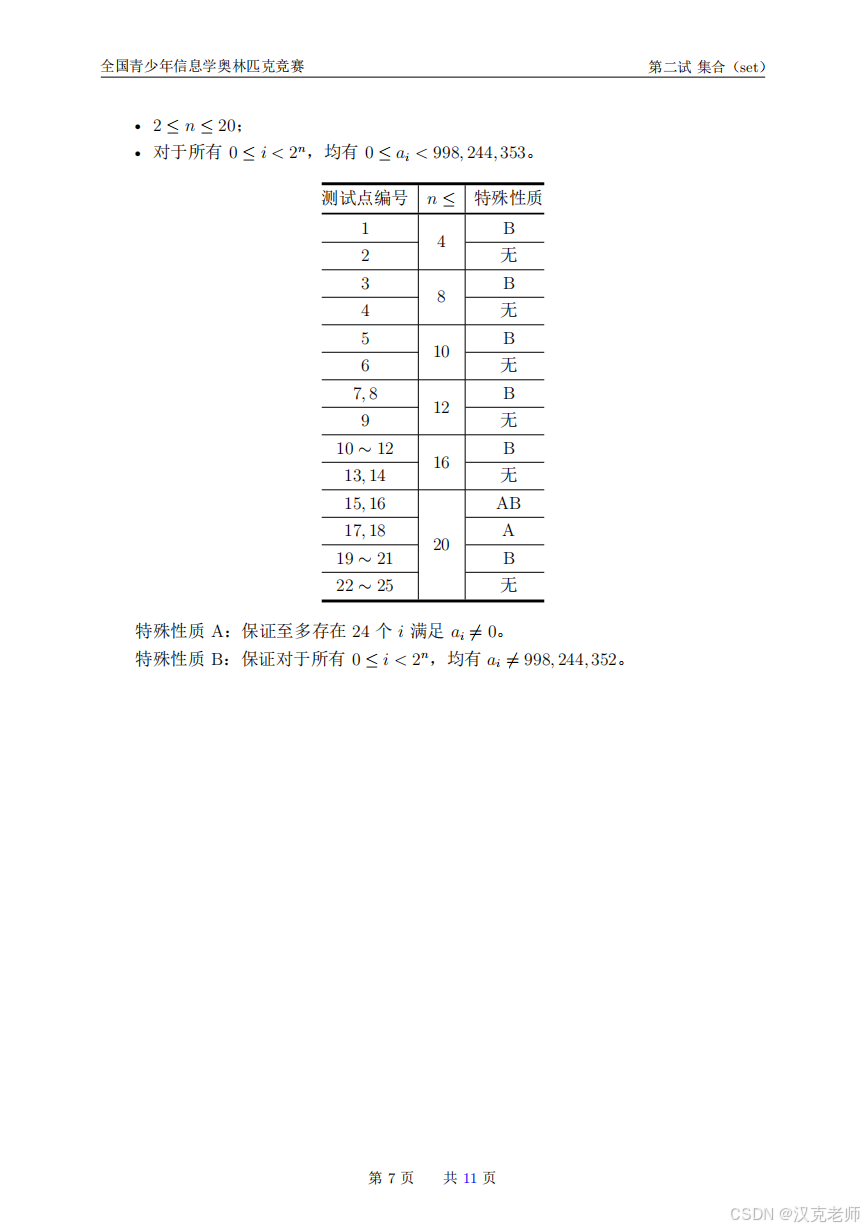
二、把题目讲成小故事

1、🌟 故事版：小精灵"集合村"的秘密力量 🌟

在一个叫做 位运算王国 的地方，住着一群编号从 0 到 2^n - 1 的小精灵。

每个小精灵 i 手中都拿着一个数 a[i]。

国王出了一个题目：

"找出所有精灵组成的各种小队（任意组合），每个小队的力量按某种特殊的公式计算，最后把所有小队的力量加起来！"

可是小队数量太多啦！光是 n=20 时，小队数量就有：

2^(2^20) （天文数字！）

根本算不过来。

于是国王召唤了三位魔法师：

🔮 魔法师 f（负责乘法小盒子）

🔮 魔法师 g（负责修正奇怪的概率）

🔮 魔法师 h（负责计算最终力量）

他们使用一种特殊的魔法药水：Milthm

2、🧪 第一章：Milthm 魔法药水是什么？

Milthm 药水长这样：

Milthm {

a ------ 正常的数

b ------ 一个"诅咒层数"

}

故事解释：

🎭 当 b = 0 时

表示这瓶药水 很正常

里面的真实数就是 a

👻 当 b > 0 时

表示它被封印了！

真实值是 0

（就像数被"吞掉"了）

这样设计是为了应对：

  • 加法结果取模可能变成 0

  • 0 不能随便求逆

  • 连续变 0 会让结果崩掉

所以，当加法取模结果变 0，我们就把 b + 1（封印层数加一）。

3、🧪 第二章：三种魔法师的道具

每个精灵 i 会生成：

🧰 （1） f[i] = Milthm(a[i] + 1)

小故事：

精灵 i 带着一个"+1 号力量水晶"；

f[i] 记录着这个水晶的魔力。

🧰 （2） g[i] 的意思是：

g[i] = (2 a[i] + 1) / (a[i] + 1)^2

小故事：

g[i] 记录这个精灵带来的"贡献修正系数"。

这个公式来自数学推导（卷积平方后要除多出来的次数）。

4、⚙️ 第三章：魔法师们开始工作（算法主线）

（1）🔥 第一阶段：子集乘积 DP（SOS DP）

魔法师 f 和 g 要把 所有包含某些精灵的小队的效果 算出来。

他们使用一台叫做：

💡 子集快速卷积机（SOS DP）

你可以把它想象成：

"如果一个集合不包含某个精灵，那我把包含这个精灵的小队力量乘过来。"

于是：

cpp 复制代码 
for 每个比特 i
    for 每个集合 S
        if S 不含 i：
            f[S] *= f[S | (1<<i)]
            g[S] *= g[S | (1<<i)]

故事解释：

对于"没有精灵 i 的队伍 S"，我们把"加上精灵 i 的队伍 S+i"的魔力乘进来。

这样 f[S] 最后就代表所有"包含在 S 的精灵组成的小队"的乘积总效果！

(2) 🔥 第二阶段：给每个 f[S] 加上一个"队伍大小的魔法系数"

cpp 复制代码 
f[S] *= (-2)^(popcount(S))
g[S] *= (2)^(-popcount(S))

你可以理解为：

队伍人越多，加的增益/削弱越大

（3）🔥 第三阶段：再次用 SOS DP 求 f 的前缀和

cpp 复制代码 
for 每个比特 i
    for S 不含 i：
        f[S+i] += f[S]

故事解释：

像"洪水向下流"，对所有 S 的上级集合累加。

最终：

f[S] = 某种"所有队伍贡献的累加值"

(4)🔥 第四阶段：平方+莫比乌斯反演求 h

cpp 复制代码 
h[S] = f[S]^2
做莫比乌斯反演

故事解释：

h[S] 记录"所有队伍 U 满足 U 的异或等于 S 的贡献总和"

(5) 🔥 第五阶段：最终整合

cpp 复制代码 
ans = Σ ( h[S] * g[S] )

故事解释：

h 说"队伍 XOR = S 时力量是这个"

g 说"但要乘一个修正因子 g[S]"

最终求和得到答案！

5、魔法师工作为什么能这么快？

因为我们始终只处理：

  • 2^n 个精灵 → 最多 1,048,576

  • 2^n 个子集 → 最多 1,048,576

  • 时间复杂度 O(n * 2^n) → 可行

而不是 2^(2^n) 那个天文数字。

6、对魔法师工作的总结：

我们的问题是：

"所有队伍力量求和，其中队伍太多数不过来，所以我们用魔法把所有队伍一起算。"

我们使用了三位魔法师：

魔法师 作用
f 合并队伍力量
g 修正贡献
h 计算 XOR 对应的队伍力量

Milthm 药水解决：

  • 加法结果变 0 时的麻烦

  • 保证取模不会坏掉

  • 能支持大量乘法和合并

最后用：

  • 两次 SOS DP

  • 一次莫比乌斯反演

  • 一次卷积平方

成功在 O(n * 2^n) 内求解！

三、参考程序：

cpp 复制代码 
#include <cstdio>
using namespace std;
typedef long long ll;

const ll mod = 998244353;
const int N = 20;

/*
====================================================
🌟 Milthm 结构：处理"集合村小精灵能量"避免取模异常
====================================================

小精灵状态相当于：
    a × (mod)^b

其中：
    a = 保留下来的"真正数字"
    b = "爆炸次数"（发生 +mod 或 *mod 时，会产生 log 层的能量）

为什么需要？
----------------
在 SOS DP 中，每个元素都会被加、减、乘很多次。
如果有时发生"加出 0"，则 mod 下"0"会被当做 0，
但真实数学上，可能是 (mod) 的倍数，不是普通 0。

因此：
    用 Milthm 来记录"真实值 = a × mod^b"

当 b > 0 时，真实值一定是"实际 0"（mod 意义下），
但不是"普通的 0"，需要在最终时判断。
*/

struct Milthm {
    ll a;   // 当前值 a
    ll b;   // 记录被 mod 掉的次数（相当于乘了 mod^b）

    Milthm() {}

    // 用普通整数构造一个 Milthm
    Milthm(ll x) {
        x %= mod;
        if (x > 0) {
            // 这是正常数
            a = x;
            b = 0;
        } else {
            // x % mod == 0，真实值可能是 mod 的倍数
            a = 1;  // 只是标记用，不重要
            b = 1;  // 标记这个数是 "mod × 某个东西"
        }
    }

    // 直接指定 a,b
    Milthm(ll a_, ll b_) {
        a = a_;
        b = b_;
    }

    // 输出"真实值"
    ll real_val() {
        // 如果 b > 0，则真实值 = 0（mod 意义下）
        return b == 0 ? a : 0;
    }
};

/*
====================================================
🌟 Milthm 运算规则
====================================================
所有运算都遵守数学意义：

    (a1 * mod^b1) + (a2 * mod^b2)

要根据 b 值判断谁更小（更"弱"），并保持 mod^b 精确记录。
*/

// 加法：小精灵力量加法
Milthm operator + (const Milthm & a, const Milthm & b) {
    // b 小的是真正"强"的，因为不被 mod 淹没
    if (a.b < b.b) return a;
    if (a.b > b.b) return b;

    // b 相同，说明可以正常相加
    ll x = (a.a + b.a) % mod;

    if (x == 0) {
        // 如果 mod 意义下变成 0，要记录"爆炸了一次"
        return Milthm(1, a.b + 1);
    } else {
        return Milthm(x, a.b);
    }
}

Milthm & operator += (Milthm & a, const Milthm & b) {
    return a = a + b;
}

// 取负号
Milthm operator - (const Milthm & a) {
    return Milthm(mod - a.a, a.b);
}

Milthm & operator -= (Milthm & a, const Milthm & b) {
    return a += -b;
}

// 乘法：a × mod^b × c × mod^d = (ac) × mod^(b+d)
Milthm operator * (const Milthm & a, const Milthm & b) {
    return Milthm(a.a * b.a % mod, a.b + b.b);
}

Milthm & operator *= (Milthm & a, const Milthm & b) {
    return a = a * b;
}

// --------------------------------------------------
// 常用函数
// --------------------------------------------------

// 快速幂
ll qpow(ll a, ll b) {
    if (a < 0) a += mod;
    if (b < 0) b += mod - 1;

    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return ans;
}

// Milthm 取逆：
//   (a × mod^b)^(-1) = a^(-1) × mod^(-b)
Milthm inv(Milthm x) {
    return Milthm(qpow(x.a, mod - 2), -x.b);
}


// 快速读入
int read() {
    int x = 0, ch;
    do ch = getchar(); while (ch < '0');
    do {
        x = x * 10 + (ch - '0');
        ch = getchar();
    } while (ch >= '0');
    return x;
}

Milthm f[1 << N], g[1 << N], h[1 << N];
ll a[1 << N];
int n;

int main() {
    read();
    int t = read();

    while (t--) {
        n = read();

        // ======================================
        // 初始化小精灵基础能量 f[], g[]
        // ======================================
        for (int i = 0; i < (1 << n); i++) {
            a[i] = read();

            // f[S] = a[S] + 1  的小精灵形式
            f[i] = Milthm(a[i] + 1);

            // g[S] = (2a+1)/(a+1)^2
            g[i] = Milthm(2 * a[i] + 1)
                   * inv(a[i] + 1)
                   * inv(a[i] + 1);
        }

        // ==============================================
        // 第一遍 SOS DP：
        //   f[S] = ∏ f[T] (T ⊇ S)
        //   g[S] = 同理
        // 小精灵收集"所有超集 T"的力量乘积
        // ==============================================
        for (int i = 0; i < n; i++) {
            for (int S = 0; S < (1 << n); S++) {
                if (((S >> i) & 1) == 0) {
                    f[S] *= f[S | (1 << i)];
                    g[S] *= g[S | (1 << i)];
                }
            }
        }

        // ======================================
        // 第二步：按故事：
        //   f[S] ×= (-2)^|S|
        //   g[S] ×= 2^(-|S|)
        // ======================================
        for (int S = 0; S < (1 << n); S++) {
            f[S] *= qpow(-2, __builtin_popcount(S));
            g[S] *= qpow(2, -__builtin_popcount(S));
        }

        // ======================================
        // 第三步：SOS 逆变换 (Zeta Inversion)
        //   f = 子集和恢复
        // ======================================
        for (int i = 0; i < n; i++) {
            for (int S = 0; S < (1 << n); S++) {
                if (((S >> i) & 1) == 0) {
                    f[S | (1 << i)] += f[S];
                }
            }
        }

        // ======================================
        // h[S] = f[S]^2
        // ======================================
        for (int S = 0; S < (1 << n); S++) {
            h[S] = f[S] * f[S];
        }

        // ======================================
        // 再做一次 Möbius 反演
        // h[S] = h[S] - h[T] (T ⊂ S)
        // ======================================
        for (int i = 0; i < n; i++) {
            for (int S = 0; S < (1 << n); S++) {
                if (((S >> i) & 1) == 0) {
                    h[S | (1 << i)] -= h[S];
                }
            }
        }

        // ======================================
        // 最终答案：
        //   sum_S h[S] * g[S]
        // ======================================
        Milthm ans = 0;
        for (int S = 0; S < (1 << n); S++) {
            ans += h[S] * g[S];
        }

        // 输出真实值
        printf("%lld\n", ans.real_val());
    }

    return 0;
}

四、程序说明：

  • Milthm ：负责处理"取模异常"，记录真实值是否被 mod 吃掉。

  • f[S]：收集"小精灵从所有超集 T 传来的力量"的乘积。

  • g[S]：是一个特殊权重，用于最后统计。

  • h[S] = f[S]^2 经过 Möbius 反演：得到"正好来自 S 的贡献"。

  • 最终 ：sum h[S] * g[S]。

全程使用 SOS DP（超集 DP） + Möbius 反演 + 防模异常 Milthm。

五、算法补充讲解（一）:子集卷积

1、什么是子集卷积

2、直观意义

3、为什么直接暴力做很慢

4、更快的思路概览（把枚举"转化"）

关键思想是：

  • 用 按"元素个数（popcount）分层" 的技巧把函数拆成"按大小（size）归类"的数组；

  • 对每一层用 子集 Zeta 变换（subset zeta） 把"子集求和"转化成在所有 mask 上做乘法；

  • 在变换域把按大小的多项式做"普通卷积"后，再用 Möbius 逆变换 恢复回原来的空间。

这种方法能把复杂度降到 O(n^2 * 2^n)（常见实现），对 n≤20 是可行的。

5、具体算法步骤（标准做法，复杂度 O(n^2 * 2^n)）

cpp 复制代码 
for bit in [0..n-1]:
    for mask in [0..N-1]:
        if mask has bit:
            F_k[mask] += F_k[mask ^ (1<<bit)]

6、为什么这一步能得到正确答案

7、完整小程序（子集和 + 恢复 + 超集和 示例）

下面给出一个清晰的实现模板（带模运算），注意这是「按大小分层 + zeta + 卷积 + inverse zeta」的标准实现，返回所有 h[mask]：

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll MOD = 998244353;

int main() {
    int n;
    cin >> n;
    int N = 1 << n;
    vector<ll> f(N), g(N);
    for (int i = 0; i < N; ++i) cin >> f[i];
    for (int i = 0; i < N; ++i) cin >> g[i];

    // 按大小分层：F[k][mask]
    vector<vector<ll>> F(n+1, vector<ll>(N, 0)), G(n+1, vector<ll>(N, 0));
    for (int mask = 0; mask < N; ++mask) {
        int k = __builtin_popcount(mask);
        F[k][mask] = (f[mask] % MOD + MOD) % MOD;
        G[k][mask] = (g[mask] % MOD + MOD) % MOD;
    }

    // subset zeta：每层单独做
    for (int k = 0; k <= n; ++k) {
        for (int bit = 0; bit < n; ++bit) {
            for (int mask = 0; mask < N; ++mask) {
                if (mask & (1 << bit)) {
                    F[k][mask] = (F[k][mask] + F[k][mask ^ (1 << bit)]) % MOD;
                    G[k][mask] = (G[k][mask] + G[k][mask ^ (1 << bit)]) % MOD;
                }
            }
        }
    }

    // 在变换域做大小卷积：Hhat[s][mask] = sum_{i=0..s} Fhat[i][mask]*Ghat[s-i][mask]
    vector<vector<ll>> Hhat(n+1, vector<ll>(N, 0));
    for (int mask = 0; mask < N; ++mask) {
        for (int i = 0; i <= n; ++i) if (F[i][mask]) {
            for (int j = 0; j + i <= n; ++j) if (G[j][mask]) {
                Hhat[i+j][mask] = (Hhat[i+j][mask] + F[i][mask] * G[j][mask]) % MOD;
            }
        }
    }

    // 逆变换（Möbius）把 Hhat -> H（每层单独做）
    for (int k = 0; k <= n; ++k) {
        for (int bit = 0; bit < n; ++bit) {
            for (int mask = 0; mask < N; ++mask) {
                if (mask & (1 << bit)) {
                    Hhat[k][mask] = (Hhat[k][mask] - Hhat[k][mask ^ (1 << bit)]) % MOD;
                    if (Hhat[k][mask] < 0) Hhat[k][mask] += MOD;
                }
            }
        }
    }

    // 最终 h[mask] = H[ popcount(mask) ][ mask ]
    vector<ll> h(N);
    for (int mask = 0; mask < N; ++mask) {
        int k = __builtin_popcount(mask);
        h[mask] = Hhat[k][mask];
    }

    // 输出或使用 h
    for (int mask = 0; mask < N; ++mask) {
        cout << h[mask] << (mask+1==N?'\n':' ');
    }
    return 0;
}

注 ：上面代码给出的是核心子集卷积计算。实际比赛里你会把 f,g 的定义替换为题目需要的值，最后可能只用 h[全局] 或者对 h 做进一步合并。

8、手算与验证

（1）手算 n=2 的子集卷积

（2）代入程序验证：

六、算法补充讲解（二）: SOS DP（Sum Over Subsets DP）

1、什么是 SOS DP

SOS DP 是一类常用的位掩码技巧，用来快速把 "对子集/超集做累加/累乘" 的操作在 O(n * 2^n) 时间内完成（而不是暴力的 O(3^n) 或更慢）。常见用途：把某个函数 f(S) 的子集和、超集和、或者把这些和用于后续的卷积/DP 等操作。

2、直观比喻

想象有 n 个开关（编号 0..n-1），每个开关可能关或开，一个配置（mask）表示哪几个开着。每个配置有一个值 f[mask]（比如每个配置的金币数）。你想知道：对于每一个配置 mask，它包含的所有子配置 （也就是可以关掉一些开关得到的那些配置）的金币总和是多少？

SOS DP 就是把"对每个 mask 找所有子配置并求和"这件事，用"把信息沿着开关一位位传递"的办法高效做完。

3、常见的两种变换（核心）

subset zeta（子集前缀和）

把 f 变成 F，使得
F[mask] = sum_{sub ⊆ mask} f[sub]（即 mask 的所有子集的和）

subset mobius（子集莫比乌斯逆变换）

f[mask] = sum_{sub ⊆ mask} μ( mask, sub ) * F[sub] ------ 用来从 F 恢复原始 f。在二进制位实现上就是 zeta 的逆操作。

（另外还有"对超集求和"的对应版本，做法类似，只是循环条件反过来。）

4、为什么能快

把按位考虑：对每一位 i（0..n-1），我们用一次循环把所有"含 i 的掩码"与"不含 i 的掩码"的关系处理好。每位处理需要 O(2^n) 次操作，一共 n 位，所以 O(n * 2^n)。这比枚举每个 mask 的所有子集（每个 mask 要枚举 2^{popcount(mask)}）要快很多。

5、具体操作（代码模板 & 解释）

目标：计算 F[mask] = sum_{sub ⊆ mask} f[sub]

实现（子集和）

cpp 复制代码 
// 计算 F[mask] = sum_{sub ⊆ mask} f[sub]
int n;              // 元素个数
int N = 1 << n;     // 掩码总数
vector<long long> f(N), F(N);

// 假设 f 已经填好
F = f; // 先拷贝
for (int bit = 0; bit < n; ++bit) {
    for (int mask = 0; mask < N; ++mask) {
        if (mask & (1 << bit)) {
            F[mask] += F[mask ^ (1 << bit)];
            // 若需要取模，记得在这里 mod
        }
    }
}

含义 ：对于每一位 bit，把那些不含 bit 的子集 的值累到含 bit 的 mask 上，从而逐位把所有子集的和累到 F[mask]。

恢复原始 f（Mobius 逆变换）

如果你有 F，想恢复 f：

cpp 复制代码 
// 假设 F 已经是 sum over subsets 的结果
vector<long long> recovered = F;
for (int bit = 0; bit < n; ++bit) {
    for (int mask = 0; mask < N; ++mask) {
        if (mask & (1 << bit)) {
            recovered[mask] -= recovered[mask ^ (1 << bit)];
            // 若取模，注意保持非负
        }
    }
}
// 现在 recovered == original f（在没有溢出/模干扰下）

这两段是互逆的：先 zeta（加），再 mobius（减）可以还原回去。

示例：n=3 的具体数值演示

设 n = 3，N = 8（mask 从 0 到 7），我们取：

f = [1,2,3,4,5,6,7,8] // f[0]=1, f[1]=2, ..., f[7]=8

我们手算 F[mask] = sum_{sub ⊆ mask} f[sub]，结果如下（我按二进制写 mask）：

mask (bin) mask (dec) f[mask] F[mask] = sum_{sub⊆mask} f[sub]
000 0 1 1
001 1 2 1 + 2 = 3
010 2 3 1 + 3 = 4
011 3 4 1+2+3+4 = 10
100 4 5 1+5 = 6
101 5 6 1+2+5+6 = 14
110 6 7 1+3+5+7 = 16
111 7 8 1+2+3+4+5+6+7+8 = 36

用上面的 zeta 代码能在 O(n * 2^n) 时间得到同样的 F。

变种：求"超集和"而不是"子集和"

如果你要求 G[mask] = sum_{sup ⊇ mask} f[sup]（mask 的所有超集的和），只需把循环的条件和方向换一下：

cpp 复制代码 
// G[mask] = sum_{sup ⊇ mask} f[sup]
G = f;
for (int bit = 0; bit < n; ++bit) {
    for (int mask = 0; mask < N; ++mask) {
        if ((mask & (1 << bit)) == 0) {
            G[mask] += G[mask | (1 << bit)];
        }
    }
}

注意：两者经常混用，写代码前先确认你要枚举子集还是超集。

常见应用场景（比赛里超实用）

  • 计算每个 mask 的子集和 或超集和（最基础）

  • 用在 子集卷积（subset convolution） 中作为子步骤

  • 进行 bitmask 状态的 DP 优化，例如合并 DP、计数划分等

  • 求每个 mask 的最小/最大值在其子集/超集中的值（把加法换成 min/max 并稍改循环顺序）

  • 用于 FFT-like 的变换（在集合上的"点值到系数"转换）

常见错误与调试建议

  1. 反方向写循环 ：子集和和超集和的 if 条件正好相反，写错会得不到期望结果。

    • 子集和：if (mask & (1<<bit)) F[mask] += F[mask^(1<<bit)];

    • 超集和：if ((mask & (1<<bit)) == 0) G[mask] += G[mask|(1<<bit)];

  2. 忘记初始化 F = f：必须先拷贝原数组，否则累加不对。

  3. 模运算忘记取模或处理负数 ：在加减时注意 mod。

  4. 误以为能直接还原到子集卷积：子集卷积还需要按大小分层并做逐层卷积，直接用 SOS 还不足够（SOS 是子集卷积的关键子步骤）。

代码演示：完整小程序（子集和 + 恢复 + 超集和 示例）

下面的 C++程序读取 n 和数组 f，计算并打印 F_sub（子集和）和 G_sup（超集和），并验证 mobius 能否还原 f。

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int main() {
    int n;
    cin >> n;
    int N = 1 << n;
    vector<ll> f(N);
    for (int i = 0; i < N; ++i) cin >> f[i];

    // 子集和 F[mask] = sum_{sub ⊆ mask} f[sub]
    vector<ll> F = f;
    for (int bit = 0; bit < n; ++bit) {
        for (int mask = 0; mask < N; ++mask) {
            if (mask & (1 << bit)) {
                F[mask] += F[mask ^ (1 << bit)];
            }
        }
    }

    // 用 Mobius 逆变换恢复 f
    vector<ll> recovered = F;
    for (int bit = 0; bit < n; ++bit) {
        for (int mask = 0; mask < N; ++mask) {
            if (mask & (1 << bit)) {
                recovered[mask] -= recovered[mask ^ (1 << bit)];
            }
        }
    }

    // 超集和 G[mask] = sum_{sup ⊇ mask} f[sup]
    vector<ll> G = f;
    for (int bit = 0; bit < n; ++bit) {
        for (int mask = 0; mask < N; ++mask) {
            if ((mask & (1 << bit)) == 0) {
                G[mask] += G[mask | (1 << bit)];
            }
        }
    }

    // 输出
    cout << "mask f[mask] F_sub[mask] recovered[mask] G_sup[mask]\n";
    for (int mask = 0; mask < N; ++mask) {
        cout << bitset<16>(mask).to_string().substr(16-n) << " "
             << mask << " "
             << f[mask] << " "
             << F[mask] << " "
             << recovered[mask] << " "
             << G[mask] << "\n";
    }
    return 0;
}

运行时可以输入 n=3 和 f = 1 2 3 4 5 6 7 8 来验证表格与我们之前的示例一致。

七、算法补充讲解（三）:取模异常（mod 异常）

1、本题中需要处理（mod 异常）

Milthm 是一个"带有阶（b）"的模数系统，用来解决在多次乘法、加法、逆变换中出现的"结果被 mod 了之后无法区分真实值是不是 0"这个问题。

也就是说：

它保证：只要真实值不是 0，那么最终 real_val() 就一定能正确返回它
如果真实值是 0，它用 (a=1, b>=1) 表示"这是某个 mod 异常形成的 0"

它是一种模拟"模意义下的唯一表示"的技巧，让复杂的卷积在 modulo 998244353 下保持数学意义上的正确性。

2、直观比喻

想象一下：

  • a 是"车上的油量"

  • 取模 998244353 就像"过收费站时会被要求把油量除以 998244353 后剩下余数继续跑"

  • 如果你油量刚好是 998244353，你经过收费站后变成 0 ------ 但你并不是"真的没有油"！

于是出现了：

"油表显示 0，但实际上你本来是满油，只是被除法系统截断了！"

这就是所谓的：

❗ 取模异常（mod 0 artifact）

比如一个数字 x = 998244353

在 mod 998244353 下是：

x % mod == 0

但 真实值不是 0！

而计算机无法知道它为什么是 0：

  • 是真实 0？

  • 还是被 mod 之后"伪装成 0"？

这种情况在卷积、逆变换、乘法累积中会反复出现，导致算法 严重错误！

3、🧨 Milthm 的目的：区分"真零"和"假零"

Milthm 定义：

cpp 复制代码 
struct Milthm {
    ll a; // 取模后的数值（余数）
    ll b; // 阶，用来记录"被 modulo 冲掉了几次"
};

当你构造 Milthm(x) 时：

cpp 复制代码 
Milthm(ll x) {
    x %= mod;
    if (x > 0) {
        a = x; 
        b = 0;      // 真实非0，没有被mod
    } else {
        a = 1;
        b = 1;      // 表示这个数是真零还是mod零？记录为"异常零"
    }
}

也就是说：

真实意义 Milthm 表示法
真零（真实值=0） a=1, b=1 但在计算链中阶数会继续增加
假零（被 mod 掉的非零） a=1, b≥1
非零真实值 a = x%mod, b = 0

最终答案 real_val()：

cpp 复制代码 
ll real_val() {
    return b == 0 ? a : 0; 
}

含义：

  • 如果没有发生异常（b=0），返回 a（真正的 mod 值）

  • 如果 b>0，说明这个数最终应该是 0

4、🔥 最关键：运算规则保证异常值正确传播

➤ 加法（避免 0 + something 被计算成错误）

cpp 复制代码 
Milthm operator + (const Milthm &a, const Milthm &b) {
    if (a.b < b.b) return a;
    if (a.b > b.b) return b;
    ll x = (a.a + b.a) % mod;
    if (x == 0) return Milthm(1, a.b+1);  // 新的异常零
    else return Milthm(x, a.b);
}

分析：

  • 如果 a、b 的阶不同，代表其中一个是真实意义更"弱"的数，取阶小者

  • 如果阶相同，进行正常模加

  • 如果结果模后变成 0，则 b++

    ------ 这是最重要的：因为我们要记住这个 "0" 是模溢出的产物，不是真零！

➤ 乘法（阶 b 累加）

cpp 复制代码 
Milthm operator * (const Milthm &a, const Milthm &b) {
    return Milthm(a.a * b.a % mod, a.b + b.b);
}

乘法作用：

  • a.a 和 b.a 正常模乘

  • 阶 b 相加

  • 每次产生的异常零会继续传播

乘法是建立整个结构正确性的另一个关键理由。

🧪 来看一个真实例子（解释为什么必须用 Milthm）

假设要计算：

(998244353 - 5) + 5

在真实数学：

998244348 + 5 = 998244353 = 0 (mod) 但真实值 ≠ 0

普通 mod 计算得到：

0

你已经永远失去真实信息！

Milthm 会这样算：

  1. (998244348 -> Milthm(a=998244348, b=0))

  2. (5 -> Milthm(a=5, b=0))

  3. 和：(a.a + b.a) % mod == 0

    → 于是产生异常零，返回 (a=1, b=1)

  4. 最终输出时，因为 b≥1，结果为 0

但 内部仍然记得：这是"假零"，不会污染接下来的卷积。

为什么这个结构必须出现在本题？

本题有：

  • 大量 乘积

  • 大量 逆元

  • 大量 子集 DP

  • 大量 卷积

  • 模数是 998244353 → 出现很多恰好模掉为 0 的情况

如果使用普通 long long mod 运算：

  • 一旦中间值出现模零，真实信息会永远丢失

  • 导致最终结果全部错

因此必须使用类似 Milthm 的技巧：

保留"这个值曾经被 mod 踩成 0 的痕迹（b）"，保证所有运算在数学意义上正确。

相关推荐
Ayu阿予2 小时前
C++从源文件到可执行文件的过程
开发语言·c++
福尔摩斯张2 小时前
基于C++的UDP网络通信系统设计与实现
linux·c语言·开发语言·网络·c++·tcp/ip·udp
mit6.8242 小时前
presum|
算法
不穿格子的程序员2 小时前
从零开始写算法——链表篇2:从“回文”到“环形”——链表双指针技巧的深度解析
数据结构·算法·链表·回文链表·环形链表
hkNaruto2 小时前
【规范】Linux平台C/C++程序版本发布调试规范手册 兼容银河麒麟
linux·c语言·c++
guygg882 小时前
基于Matlab的压缩感知信道估计算法实现
开发语言·算法·matlab
诺....3 小时前
C语言不确定循环会影响输入输出缓冲区的刷新
c语言·数据结构·算法
热门推荐
01GitHub 镜像站点02【AutoGLM部署】本地私有化部署AI手机Agent03UV安装并设置国内源04Open-AutoGLM Windows 安装部署教程05【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）06Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08Linux下V2Ray安装配置指南09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10BongoCat - 跨平台键盘猫动画工具