RF Power Amplifiers for Wireless Communications 第三章学习笔记

目录

• 章节导读与精读
• 本章相关公式推导
• 中文参考译文
• • [3.1 Introduction](#3.1 Introduction)
  • [3.2 Reduced Conduction Angle---Waveform Analysis](#3.2 Reduced Conduction Angle—Waveform Analysis)
  • [3.3 Output Termination](#3.3 Output Termination)
  • [3.4 Reduced Conduction Angle Mode Analysis---FET Model](#3.4 Reduced Conduction Angle Mode Analysis—FET Model)
  • • [Case 1: Class A](#Case 1: Class A)
    • [Case 2: Class AB](#Case 2: Class AB)
    • [Case 3: Class B](#Case 3: Class B)
    • [Case 4: Class C](#Case 4: Class C)
  • [3.5 Reduced Conduction Angle Mode Analysis---BJT Model](#3.5 Reduced Conduction Angle Mode Analysis—BJT Model)
  • [3.6 Effect of I-V "Knee"](#3.6 Effect of I-V “Knee”)
  • [3.7 Input Drive Requirements](#3.7 Input Drive Requirements)
  • [3.8 Conclusions](#3.8 Conclusions)
  • 参考文献

章节导读与精读

3.1小节概述本章将介绍通过减少导通角改变放大器模式 ，得到多类放大器。并提到功率利用因子的概念，指出效率和功率利用率是需要关注的两个方面。

3.2小节从波形的角度分析减小导通角与工作模式的关系 ，并使用傅里叶分析输出，指出不同模式与不同分量的关系。

3.3小节从放大器输出终端 的角度，基于理想假设（谐波短路），分析并计算功率和效率。

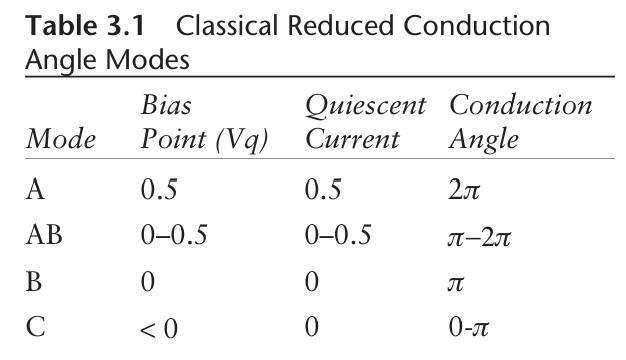
3.4小节通过使用理想的FET模型分析减小导通角的影响 ，并分别给出了A、AB、B和C类四种放大器及其对应-3 dB 降额输入的结果和分析。

3.5小节先提出了BJT模型尽管原理不同，但仍存在分析AB\C类工作模式的合理性 。因此，通过理想化的BJT模型可以搭建与FET类似的放大器，虽然存在一些轻微的差异。

3.6小节基于已有的理想模型分析，考虑了knee电压的存在，引入后分析并修正结果。

3.7小节从输入端条件 ，分别分析了输入阻抗和驱动条件对放大器的影响。指出了BJT比FET在某些情况下具有优势，以及可以通过波形整形为输入端提供合适的驱动。

本章相关公式推导

波形分析、傅里叶级数分析、效率、降额输入输出等公式推导，另起一篇文章

中文参考译文

3.1 Introduction

本章将介绍所谓传统的、或称为"减小导通角"的高效率放大器模式，即熟悉的 Class AB、Class B 和 Class C 配置。

通过将有源器件偏置到较低的静态电流，并依靠射频驱动信号将器件推入导通区，以实现更高效率的 RF 放大器，这一概念十分古老，可以追溯到真空管的早期时代。因此，它常常被认为是一个基础主题，不值得过多讨论。然而，我们将看到，在基于理想器件模型的一些基础分析中，会出现许多在现代无线通信系统背景下非常重要的问题。

比通常在基础教材中呈现的更直接但更详细的分析将表明，仅仅减少 RF 功率器件的导通角是必要条件，但往往不足以获得有意义的效率提升。通常，还需要将驱动电平从 Class A 状态显著提高，并在信号频率的谐波上提供适当的阻抗终端。许多旧教材假定 PA 器件输出端所有高次谐波都会被短路处理。这简化了分析，并且在真空管放大器时代更容易实现。然而，这种假设导致了关于当今晶体管器件应采用何种匹配拓扑结构的一些混淆，这个主题将在第 4 章中进一步讨论。

现代无线系统对 PA 设计者提出了严峻的要求。手机终端的 PA 必须尽可能高效，以节省电池功率。基站也需要满足效率要求，因为存在功耗和散热限制。在比较不同 PA 配置时，一个非常重要的概念是所谓的"功率利用因子"（PUF）。本章将对此进行定义，其基本含义是：某模式下器件所输出的 RF 功率，与该器件作为简单 Class A 放大器所能输出的功率之比 。PUF 反映了成本效益，即"每美元瓦数"。在固态器件领域，如果某种高效率配置仅能输出该器件在 Class A 模式下 RF 功率的一半，即使效率高达 95%，仍需使用两个芯片（或一个面积加倍的芯片）来满足指定的输出功率需求。这不仅仅是花费加倍的问题；更大的芯片通常具有更低的增益和更窄的匹配带宽。

无线系统通常采用包络幅度可变的调制方式。该主题将在后续章节深入讨论，但在分析传统的高效率模式时也非常重要。因此，有必要研究 Class AB 模式在不同输入功率水平下的行为。这是第 3.5 节的主题，其中包含一些令人意外的结论。

3.2 Reduced Conduction Angle---Waveform Analysis

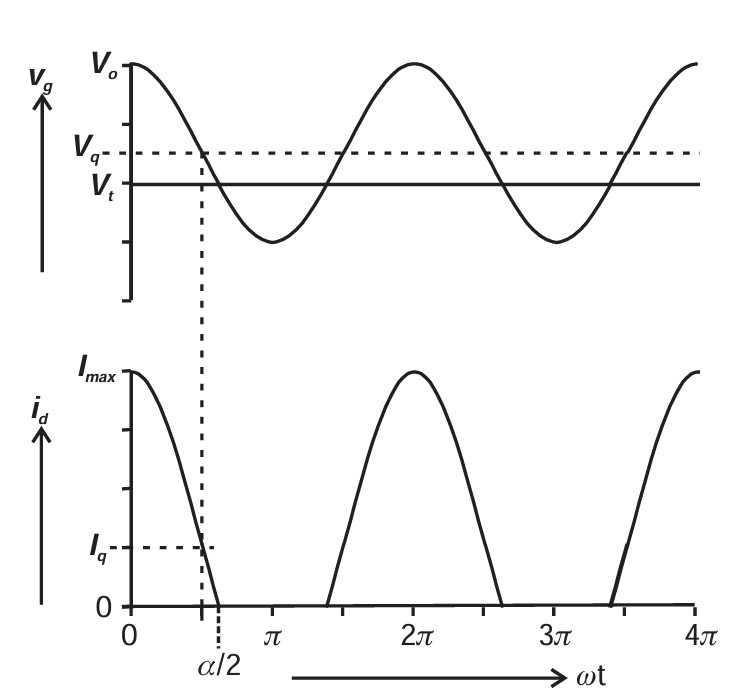
图3.1 Reduced conduction angle current waveform.

减小导通角的基本过程如图 3.1 所示。器件被偏置在超出 Class A 条件、接近截止的位置。很明显，如果 RF 驱动幅度足够大，在射频周期的负半周期，器件将被推到其截止点 V_t 之外。同样显然的是，为了使电流摆动到理想化的饱和点 I_max，驱动电平必须从 Class A 状态提高。定量而言，所需的信号电压幅度为
V s = ( 1 − V q ) ( 3.1 ) V_s=(1-V_q)\quad(3.1) Vs=(1−Vq)(3.1)

其中 V_q 是归一化的静态偏置点，定义为
V t = 0 , V o = 1 V_t=0, V_o=1 Vt=0,Vo=1

最初，将假设当静态偏置点变化时，信号电压将按照式 (3.1) 增加，以保持峰值电流为 I_max。同时暂时假设器件是理想跨导型的，并且输出电压被保持在零以上，以维持器件导通。关于输出 RF 负载的考虑将在后续部分详细讨论。

因此，器件中的电流呈现熟悉的截断正弦波形。导通角 α 表示 RF 周期中器件导通的部分。在本章中我们选择使用余弦函数描述电流波形。由于余弦函数在时间轴零点左右是对称的，因此导通角的定义曾引起一些混淆。在本书中，我们采用一种可能非标准但数学更严谨的定义，即 α 表示整个导通角度，包括时间零点两侧相等的部分。因此，电流截止点为 ωt=±α/2。现在可以根据静态偏置点和导通角，对传统的工作模式进行定义，如表 3.1 所示。

观察图 3.1 中的电流波形，可以直观地看出随着导通角减小，平均分量（即直流电源消耗）将减少。但较不明显的是基波分量会发生什么变化，并且显然会产生谐波。这些问题都可以通过对波形进行傅里叶分析来获得答案。

射频电流波形可以写成：
i d ( θ ) = I q + I p k ⋅ c o s θ , − α / 2 < θ < α / 2 ; = 0 , − π < θ < − α / 2 ; − α / 2 < θ < π i_d(\theta)=I_q+I_{pk}\cdot cos\theta, -\alpha/2<\theta<\alpha/2; \\=0,-\pi<\theta<-\alpha/2;-\alpha/2<\theta<\pi id(θ)=Iq+Ipk⋅cosθ,−α/2<θ<α/2;=0,−π<θ<−α/2;−α/2<θ<π

其中 c o s ( α / 2 ) = − ( I q I p k ) cos(\alpha/2)=-(\frac{I_q}{I_{pk}}) cos(α/2)=−(IpkIq)，且 I p k = I m a x − I q I_{pk}=I_{max}-I_q Ipk=Imax−Iq，

所以 i d ( θ ) = I m a x 1 − c o s ( α / 2 ) ⋅ ( c o s θ − c o s ( α / 2 ) ) i_d(\theta)=\frac{I_{max}}{1-cos(\alpha/2)}\cdot(cos\theta-cos(\alpha/2)) id(θ)=1−cos(α/2)Imax⋅(cosθ−cos(α/2))。

其平均电流（直流分量）为：
I d c = 1 2 π ⋅ ∫ − α / 2 α / 2 I m a x 1 − c o s ( α / 2 ) ⋅ ( c o s θ − c o s ( α / 2 ) ) ⋅ d θ I_{dc}=\frac{1}{2\pi}\cdot \int_{-\alpha/2}^{\alpha/2}\frac{I_{max}}{1-cos(\alpha/2)}\cdot (cos\theta-cos(\alpha/2))\cdot d\theta Idc=2π1⋅∫−α/2α/21−cos(α/2)Imax⋅(cosθ−cos(α/2))⋅dθ

第 n 次谐波的幅度为：
I n = 1 π ⋅ ∫ − α / 2 α / 2 I m a x 1 − c o s ( α / 2 ) ⋅ ( c o s θ − c o s ( α / 2 ) ) ⋅ c o s n θ d θ I_{n}=\frac{1}{\pi}\cdot \int_{-\alpha/2}^{\alpha/2}\frac{I_{max}}{1-cos(\alpha/2)}\cdot (cos\theta-cos(\alpha/2))\cdot cosn\theta d\theta In=π1⋅∫−α/2α/21−cos(α/2)Imax⋅(cosθ−cos(α/2))⋅cosnθdθ

由于选择了偶函数作为射频电流波形，因此不存在正交分量。

对这些积分进行求值（直到 n = 5）的结果显示在图 3.2 中，但最重要的 I_dc 和 I₁ 的结果为：
I d c = I m a x 2 π ⋅ 2 ⋅ s i n ( α / 2 ) − α ⋅ c o s ( α / 2 ) 1 − c o s ( α / 2 ) ( 3.2 ) I 1 = I m a x 2 π ⋅ α − s i n α 1 − c o s ( α / 2 ) ( 3.3 ) I_{dc}=\frac{I_{max}}{2\pi}\cdot\frac{2\cdot sin(\alpha/2)-\alpha\cdot cos(\alpha/2)}{1-cos(\alpha/2)}\quad(3.2) \\I_1=\frac{I_{max}}{2\pi}\cdot\frac{\alpha- sin\alpha}{1-cos(\alpha/2)}\quad(3.3) Idc=2πImax⋅1−cos(α/2)2⋅sin(α/2)−α⋅cos(α/2)(3.2)I1=2πImax⋅1−cos(α/2)α−sinα(3.3)

图3.2 Fourier analysis of reduced conduction angle current waveforms.

更仔细观察图 3.2 的曲线，可以看到随着导通角减小，直流分量单调下降。特别地，Class B 条件下 α = π \alpha=\pi α=π在式 3.2中可得到：
I d c ( C l a s s B ) = I m a x / π I_{dc}(Class B)=I_{max}/\pi Idc(ClassB)=Imax/π

可与 Class A 条件比较，在 Class A 中
I d c ( C l a s s A ) = I m a x / 2 I_{dc}(Class A)=I_{max}/2 Idc(ClassA)=Imax/2

此外，Class B（ α = π \alpha=\pi α=π）的基波分量在式 3.3 中为
I 1 ( C l a s s B ) = I m a x / 2 I_{1}(Class B)=I_{max}/2 I1(ClassB)=Imax/2

这当然与 Class A 条件下的基波分量相同。因此，仅从电流波形角度看，似乎有可能在不改变基波成分的情况下，将直流功率消耗降低 π/2 倍。换句话说，效率可从 Class A 的 1/2 提高到 Class B 的 π/4（约 78.5%）。但要实现这些可能性，还必须考虑输出端的终端网络以及电压波形。

对于导通角小于 π 的情况，即 Class C 工作，直流分量继续下降，但电流基波分量也开始低于 Class A 的水平。这将造成效率进一步提高，但 PUF（功率利用因子）降低；基波功率将低于晶体管的 Class A 额定输出。有关内容将在后续章节进一步讨论。

• 导通角与效率和功率存在一定的制约：增大导通角可以使得效率得到提高，但是代价是输出功率降低，即PUF降低；同时效率提高是基于理想的工作条件下，使得电压电流的摆幅在周期内达到最大。

前几个谐波的幅度也绘制在图 3.2 中。注意在 Class AB 范围内以及一直到 Class B 中点，除了基波之外最大的谐波是二次谐波。它是正的（与基波同相），从频域的角度讲，部分截止的晶体管会产生相当大的二次谐波，它会减少基波正弦波的谷值并使峰值更尖锐，从而在整体峰-峰幅度近似不变的情况下降低平均电平。顺便指出，利用晶体管的截止特性并不是生成这种理想二次谐波成分的唯一方法。例如，可以通过调整输入匹配网络的频率响应，使驱动电压具有适当的、与基波同相的二次谐波增强（假定该驱动来自另一非线性放大器级）。这带来一些有趣的可能性（见 3.7 节），因为我们将看到传统依赖截止特性的方式在驱动功率方面相当低效------这在 GHz 频段尤其重要，因为功率晶体管的增益往往十分有限。

图 3.2 中可见奇次谐波在 Class B 点处穿过零，但在 AB 模式中，三次谐波并非可以忽略。然而，在幅度低于约 0.1 的情况下，跨导特性的弱非线性成分可能显著改变整体的线性情况。但需要指出的是，在 Class B（α=π）附近进行小幅度偏置调节，可以作为控制三次谐波成分精确水平的可行方法；这将在后续 Class F 放大器的讨论中显得非常重要。

3.3 Output Termination

很明显，晶体管电流中包含一些显著的谐波分量，尤其是二次谐波。因此，在给定负载条件下分析并绘制产生的电压波形是一个更复杂的问题。首先，可以通过假设所有谐波都呈现短路来大幅简化分析；实际上，这一条件构成经典或传统高效率放大器模式定义的一部分。我们将看到，对于现代固态器件设计而言，这一假设是相当理想化的。然而，大多数旧教材之所以采用这一假设，有以下三个原因：

1. 谐波短路与基波最佳电阻匹配结合时，总能在性能上接近采用多个谐波终端（这些替代方案将在后续章节 4 和 5 中讨论）的更优解决方案。
2. 谐波"短路"在老式电子管功放中非常容易实现。对于即便是千瓦级的器件，其负载线阻抗依然以 kΩ 计，因此一个简单的并联谐振电路即可轻松实现谐波短路。
3. 在这种假设下，分析大大简化，因为输出射频波形将简化为单一正弦波。

因此，我们将在这种经典的简化假设下继续分析传统的高效率模式，但同时需要仔细审视这种假设的影响，并最终对其进行修改。

图 3.3 给出了进一步分析所需的电路。减小导通角后的电流波形流过一个交流耦合的负载，该负载包括用于基波的负载电阻，以及一个概念性的谐波短路，这里通过并联在基波频率上的并联谐振电路表示。所有谐波在负载端都被短路，因此不会产生电压，所以漏极电压是一个正弦波，其幅度通过负载电阻设定，以产生最大允许的电压摆幅，其方式与前面讨论的 Class A 放大器相似。在本分析中，我们将假设，当输入驱动电平使峰值电流达到 I_max 时，会产生最大电压摆幅。在这些假设下，通过适当选择负载电阻，可以直接使用图 3.2 的曲线计算输出功率和效率，因为在每种情况下，晶体管端的基波射频输出电压均为幅度为 V_dc 的正弦波。

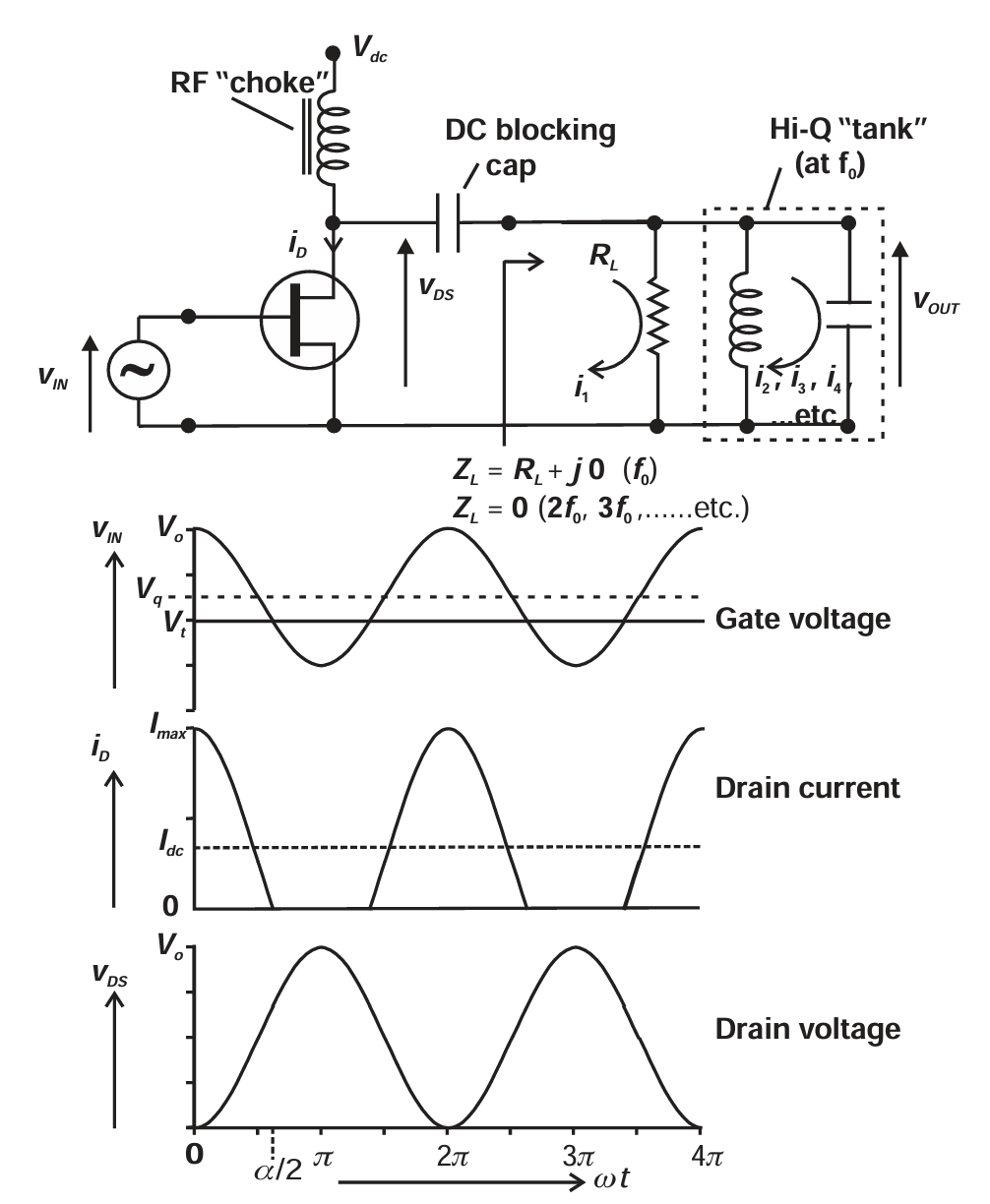
图3.3 Circuit and waveforms for analysis of reduced conduction angle amplifier modes.

因此，基波射频输出功率为：
P 1 = V d c 2 ⋅ I 1 2 ( 3.4 ) P_1=\frac{V_{dc}}{\sqrt{2}}\cdot\frac{I_1}{\sqrt{2}}\quad(3.4) P1=2 Vdc⋅2 I1(3.4)

其中I₁由公式 (3.3) 给出，而直流电源电流为：
P d c = V d c ⋅ I d c ( 3.5 ) P_{dc}=V_{dc}\cdot I_{dc}\quad(3.5) Pdc=Vdc⋅Idc(3.5)

其中 I_dc 由公式 (3.2) 给出。

输出效率定义为：
η = P 1 P d c ( 3.6 ) \eta=\frac{P_1}{P_{dc}}\quad(3.6) η=PdcP1(3.6)

除非另有说明，本书将采用此效率定义。这种做法通常会让系统设计人员不太满意，因为他们更倾向于考虑驱动功率，而在射频功率放大器中，驱动功率往往是相当可观的。这导致了另一种效率定义，即所谓的"功率附加效率"（PAE）：
P A E = P 1 − P I N P d c ( 3.7 ) PAE=\frac{P_1-P_{IN}}{P_{dc}}\quad(3.7) PAE=PdcP1−PIN(3.7)

其中 P_IN 为射频驱动功率。一般来说，如果射频功率增益小于 10 dB，那么驱动功率的需求将开始严重削弱 PA 级的漏极（或输出）效率，而且效率越高，这种影响就越严重。另一方面，设计者通常可以通过增加增益来改善情况，例如缩小带宽、恰当地使用一些正反馈、改进封装，或者使用"更高性能"的工艺技术。在这方面，将增益和输出效率视为两个独立因素是有益的，同时明确在系统级或多级 PA 级中，它们将共同影响整体效率。

• P₁-P_IN就等于对基波的增益，如果增益过低，增大大P_dc可以获得较大输出，但是此时PAE会变小；最优应该是提高增益。
  
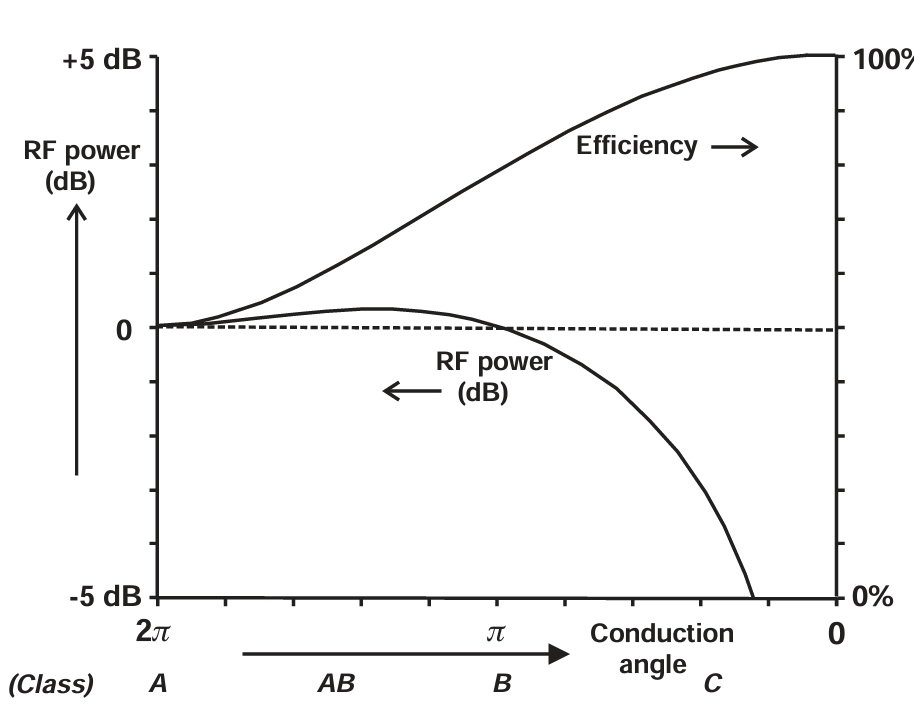
  图3.4 RF power (relative to Class A) and efficiency as a function of conduction angle; optimum load and harmonic short assumed.

因此，可以将公式 (3.2) 到 (3.6) 的结果绘制出来，以显示输出功率和效率随导通角变化的总体情况。这些结果如图 3.4 所示。假设理想条件：完美的谐波短路、线性电流摆幅达到 I_max，以及最大电压摆幅为 2·V_dc，且无拐点区。在这些条件下，负载电阻的最优值为：
R O P T = V d c / I 1 ( 3.8 ) R_{OPT}=V_{dc}/I_1\quad(3.8) ROPT=Vdc/I1(3.8)

其中 I₁ 是电流的基波傅里叶分量，由公式 (3.3) 给出，并在图 3.2 中绘出。我们已经注意到，Class B 条件下的基波分量与 Class A 相同，前提是增加驱动电压幅度以获得相同的射频峰值电流 I_max。因此，Class B 的负载电阻值便与上一章中广泛讨论的线性负载线值相同。从理论上讲，对于 Class AB 操作，这个值应稍微降低：在中间 AB 范围内约低 10%，以补偿基波幅度相较于 Class A 的小幅增加。在实际中，考虑到弱非线性效应以及更现实的拐点导通区域，实际最优值至少会有所调整 10%，因此通常在初期忽略 AB 区域的理论变化。

Class AB、B 和 C 操作的主要特征可以从图 3.4 的曲线中确定，接下来的章节将对其进行更详细的讨论。但在这里可以先总结几个要点：

1. 在 Class A 和 Class B 操作之间，基波射频输出功率基本保持不变，在中间 AB 区域相比 Class A 输出略有几分贝的增加。
2. Class B 条件下输出功率与 Class A 相同，但直流电源减少 π/2 倍，理想效率为 π/4。
3. Class C 条件下，随着导通角减小至较低值，效率持续提高；然而，这伴随着射频输出功率的大幅下降。

3.4 Reduced Conduction Angle Mode Analysis---FET Model

本节将通过考虑一些具体案例，进一步说明和分析各种常规的降导通角模式。这些案例使用 Excel 电子表格（AB_Waves）进行分析，该表格计算给定偏置和输入信号幅度条件下 RF 电流波形的傅里叶分量。初始情况下，假设器件特性为理想化。

该程序需要三个输入参数，全部为归一化电压：

• V_q 是输入直流偏置点，归一化（本书中一致）在 0（截止、电压阈值或关闭）到 1（饱和或开通通道）之间。程序假设理想强非线性跨导模型，输入电压范围可以超过这些限制，分别假设为截止或硬饱和。
• V_s 是输入信号的幅度，假设为正弦信号。为了获得最大电流摆幅（即摆动至 I_max），V_s 的值应选择为：
  V s = 1 − V q V_s=1-V_q Vs=1−Vq
• R_L 是基波负载电阻的归一化值。该值由用户选择，R_L 相对于 Class A 负载线值归一化为 1。

因此，器件电流 i_d 定义为：
i d = g m ⋅ I m a x 2 ⋅ ( V q + V s c o s θ ) , ( V q + V s c o s θ ) > 0 , = 0 , ( V q + V s c o s θ ) < 0 i_d=g_m\cdot \frac{I_{max}}{2}\cdot (V_q+V_scos\theta),(V_q+V_scos\theta)>0, \\=0,(V_q+V_scos\theta)<0 id=gm⋅2Imax⋅(Vq+Vscosθ),(Vq+Vscosθ)>0,=0,(Vq+Vscosθ)<0

其中跨导 g_m 仅用于避免量纲冲突，并假设其归一化值为 1。在此计算中，峰值电流 I_max 也归一化为 1。

对于选定的 V_q 值，可以在零到最大驱动电平（1--V_q）之间选择 V_s 值。构建电流波形，并计算直流分量和基波分量，即 I_dc 和 I₁。如果假设输出谐波短路，则 RF 输出功率为
P R F = I 1 2 R L 2 ( 3.9 ) P_{RF}=\frac{I_1^2R_L}{2}\quad(3.9) PRF=2I12RL(3.9)

该功率可直接与 Class A 功率比较，其归一化值为 1 2 \frac{1}{2} 21。相应的直流供电电流 I_dc 也可直接与 Class A 的归一化值 I_max/2（即 1 2 \frac{1}{2} 21）进行比较。因此，对于每个 V_q 值的最大驱动电平，可以相对于 Class A 条件计算效率
η = 1 2 ⋅ I 1 I d c ( 3.10 ) \eta=\frac{1}{2}\cdot\frac{I_1}{I_{dc}}\quad(3.10) η=21⋅IdcI1(3.10)

这里假设允许完整的轨到轨电压，并且负载电阻的值为
R L = R A ⋅ I 1 1 2 ( 3.11 ) R_L=R_A\cdot \frac{I_1}{\frac{1}{2}}\quad(3.11) RL=RA⋅21I1(3.11)

其中 R_A 为 Class A 负载线电阻值。

在计算"降低驱动电平"信号下的功率和效率时，通常假设负载电阻保持不变，即维持在峰值功率条件下的最优值。因此，降低驱动电平条件下的功率可以使用公式 (3.9) 计算，效率则由以下公式给出
η p b o = η m a x I d c m a x I d c I 1 I 1 m a x \eta_{pbo}=\eta_{max}\frac{I_{dc max}}{I_{dc}}\frac{I_1}{I_{1 max}} ηpbo=ηmaxIdcIdcmaxI1maxI1

其中，"max"后缀指的是最大驱动电平下 I_dc 和 I₁ 的相应值。需要注意的是，降低驱动电平的效率并非由公式 (3.10) 给出，后者给出的是在实际情况下通过增大负载电阻以维持轨到轨电压摆幅时的效率。

Case 1: Class A

Class A 条件为检查输出显示以及功率和效率提供了起点和参考点。理想 Class A 条件所需的输入为：
V q = 0.5 ; V s = 0.5 ; R L = 1.0 V_q=0.5; V_s=0.5;R_L=1.0 Vq=0.5;Vs=0.5;RL=1.0

相应的输出如图 3.5 所示。

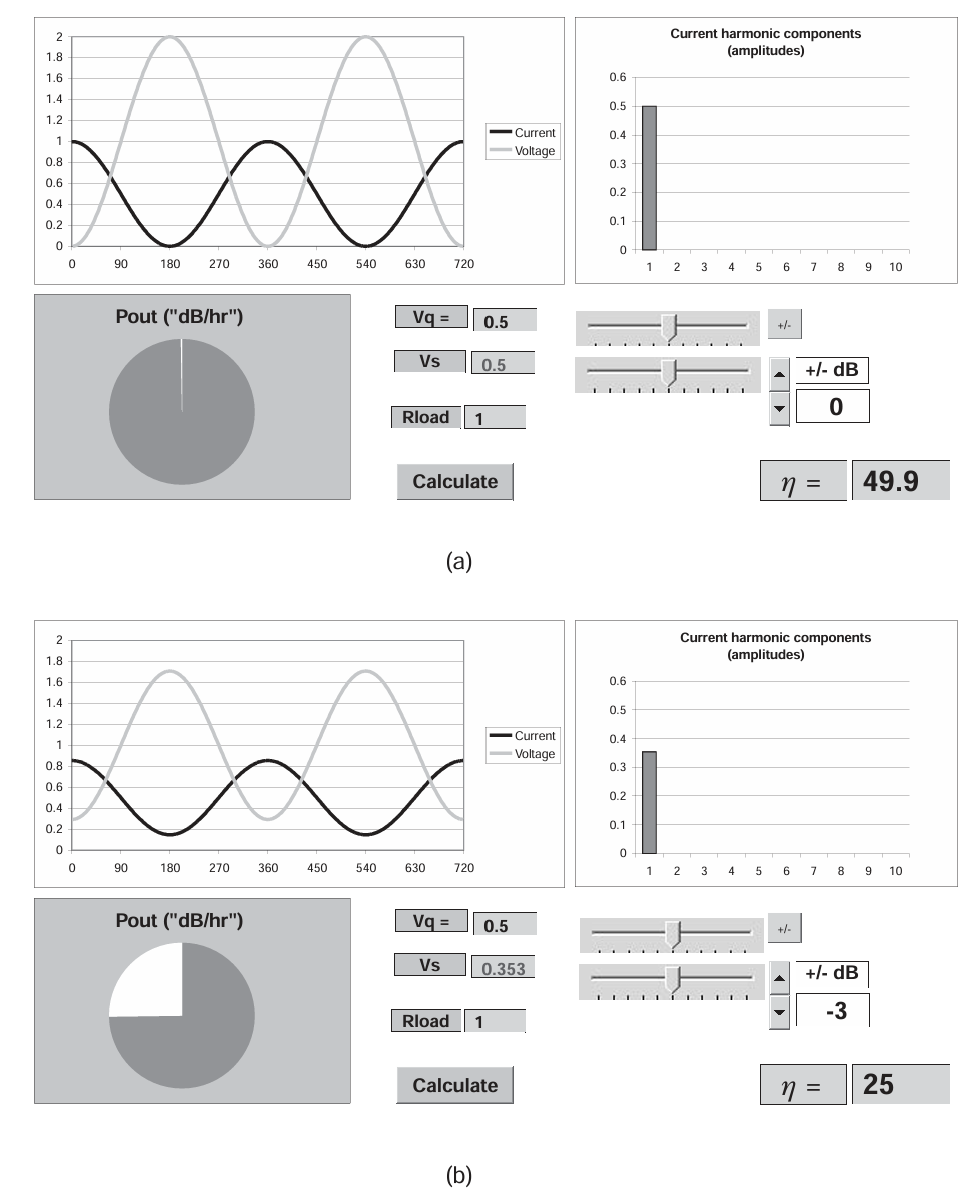
图3.5 Class A mode: (a) full drive, and (b) 3 dB backoff conditions.

该显示没有任何意外，与理想的负载线匹配线性放大器一致，显示输出效率为 50%。在全驱动条件下，功率计显示 0 dB，表示功率利用因子为 1。后续的其他情况将以此条件作为功率参考。由于负载电阻的最优选择，输出电压的正弦幅值为 V_dc，输出效率为 50%。

图 3.5(b) 显示了同一放大器在驱动电平降低 3 dB 时的情况。对于当前序列，假设晶体管的输入阻抗保持不变，因此输入功率下降 3 dB 对应电压摆幅幅值降低了 2 \sqrt{2} 2 倍。还假设输出负载条件（尤其是负载电阻值）在输入功率变化时保持不变。因此，在这种情况下，输出电压和电流摆幅也将按相同的 2 \sqrt{2} 2 因子减小。由此，输出功率如预期下降 3 dB，与线性放大器一致。然而需要注意的是，在 3 dB 降驱动条件下，效率却下降到令人担忧的 25%。顺便指出，如果为了降低驱动条件将负载电阻增加 2 \sqrt{2} 2 倍，最大电压摆幅可以恢复，同时 RF 功率和效率也相应增加。但这样会产生一个新的、更低的最大线性功率；负载电阻不能随着驱动电平的变化而简单调整。

Case 2: Class AB

中间 Class AB 条件的输入参数为：
V q = 0.3 ; V s = 0.7 ; R L = 0.94 V_q=0.3; V_s=0.7;R_L=0.94 Vq=0.3;Vs=0.7;RL=0.94

相应的输出波形如图 3.6 所示。注意，R_L 的值现在已从 Class A 负载线值降低，反映了基波电流分量的增大。RF 输出相较于 Class A 条件显示了小幅增加（0.25 dB，功率计盒子阴影反转表示），同时伴随着器件电流的直流分量显著下降。这带来了效率的有益提升（68%）。这种有利效果仅以增加驱动功率为代价。相比于 Class A 操作， V_s 从 0.5 增加到 0.7，理想情况下对应约 3 dB 的额外驱动功率，可被视为整体功率增益相对于 Class A 模式的降低。如果线性增益起始低于 10 dB，则功率附加效率提升将明显不如理想。

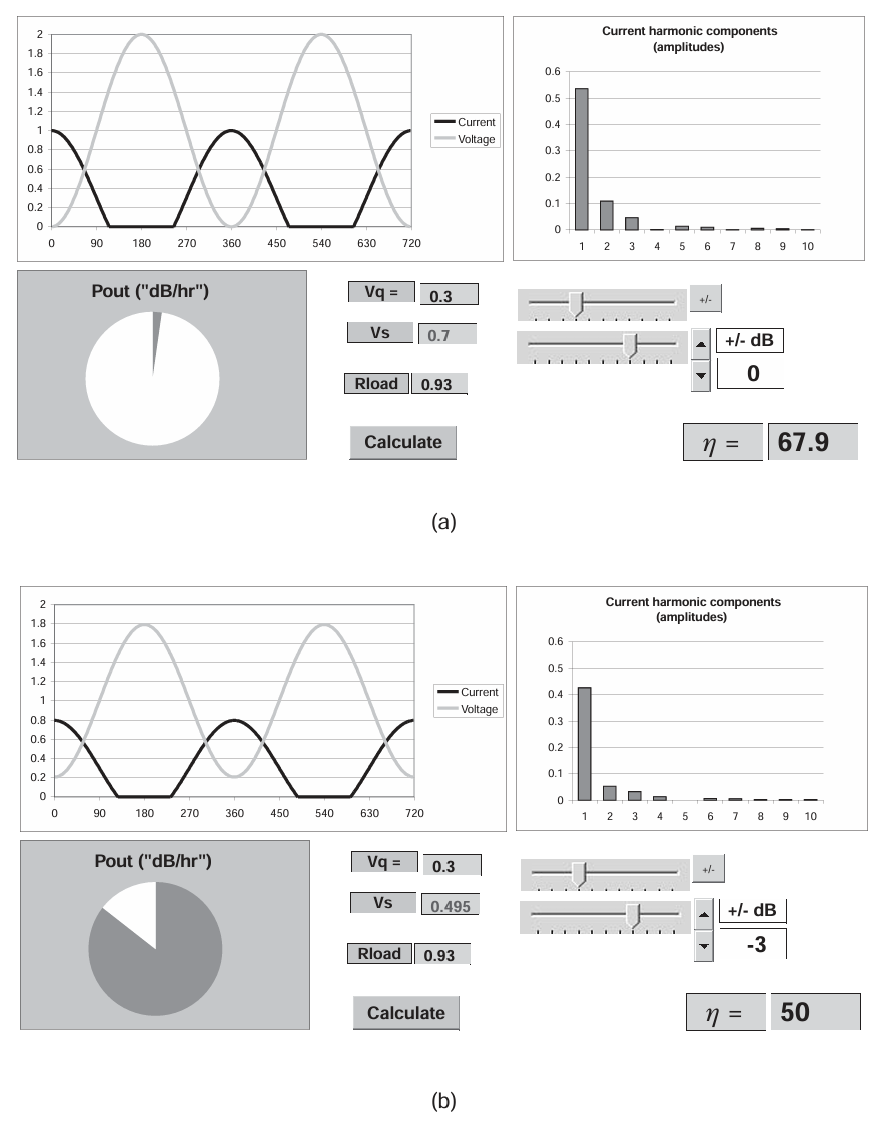
图3.6 Class AB operation, I_q = 0.3: (a) full drive, and (b) 3 dB backoff.

理想 Class AB 操作中有一个重要问题常被忽视。图 3.6(b) 显示了驱动电平降低 3 dB 的影响，与 Class A 情况不同，输出功率并未出现相应的 3 dB 下降。换句话说，这不是一个线性放大器；在此峰值功率下，幅度调制信号的包络将发生明显失真。原因在于一个简单的数学事实：在 Class AB 操作中，导通角不仅依赖于静态偏置点，也依赖于驱动电平。这可能会让经验丰富的功率放大器工程师感到意外，他们经常实验发现 Class AB 可以提供类似于 Class A 操作的有效线性动态范围。这个看似与实践的冲突将在后文（见第 3.5 节）中解释，但并不会以任何方式否定当前的观察结果。

Case 3: Class B

Class B 条件的输入参数为：
V q = 0 ; V s = 1.0 ; R L = 1.0 V_q=0; V_s=1.0;R_L=1.0 Vq=0;Vs=1.0;RL=1.0

相应的输出波形如图 3.7 所示。RF 功率已恢复到其原始（Class A）值，对应于 PUF 为 1。与 Class A 条件相比，直流电源降低了 2/π 倍，效率为 π/4，约 78.5%；这是一个经典结果。

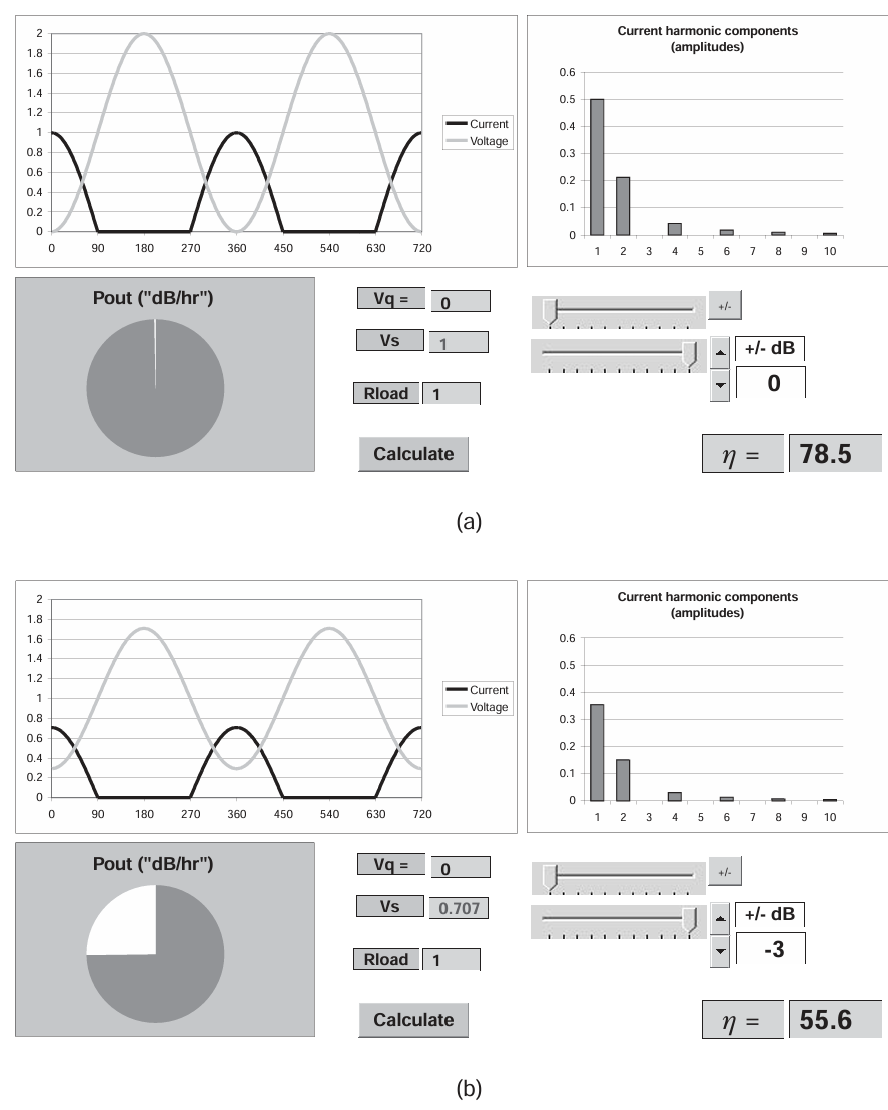
图3.7 Class B operation, V_q= 0: (a) full drive, and (b) 3 dB PBO.

缺点是，理论上为了达到所示的 Class B 条件，需要额外约 6 dB 的驱动功率。这在 RF 和微波频率下会显著降低功率增益，而在这些频段，即使线性增益高于 10 dB 也是一种奢侈。一方面，这指向了使用更高增益器件技术的必要性。GaAs HBT 和 PHEMT 技术在 2 GHz 以下的手机 PA 中的广泛应用就是这一问题的体现。另一方面，也应公平指出，BJT 器件在功率增益下降方面表现比前面考虑的 FET 器件稍好。为了生成所需的电流波形，已注意到可以利用输入端适当的非线性特性，以降低正弦信号的高驱动需求。BJT 在一定程度上通过其输入二极管结的 I-V 特性实现了这一点，Class B 的功率增益降低可能仅约 2 dB。即便是 FET 器件，也可以设法将输出产生的部分二次谐波加入输入驱动信号，从而降低 Class B 操作所需的基波驱动幅度。此问题将在第 3.7 节中进一步讨论。

然而，Class B 模式在降低驱动条件下的线性度表现出了明显优势，如图 3.7(b) 所示的 3 dB 降额条件。由于驱动信号相对于截止电平的对称性，导通角随驱动电平变化而保持恒定。因此，驱动功率降低 3 dB 将导致输出功率相应降低 3 dB，Class B 放大器表现出线性特性 。在固定负载电阻值下，3 dB 降额条件下的效率降低至 55%。在该驱动电平下，通过增加负载电阻值并允许更大的电压摆幅，可以提高输出功率和效率。事实上，如果电压摆幅被允许恢复到最大值（使用 √2Ropt 的电阻值），效率将回到 78.5%。尽管乍看似乎不切实际，但它为改善可变信号幅度范围（如幅度调制信号）下的效率提供了可能。这一点最早在 1936 年 Doherty 的经典论文中提出^[1]，将在第 10 章详细讨论。

需要注意的是，这里的"线性"是指最终正弦输出信号水平，假设所有谐波电压都被短路。乍看之下，将 Class B 器件描述为放大器，甚至是线性放大器，似乎不太合适。显然，内部存在高度非线性过程，但功率输入-输出特性显示出线性行为。

Case 4: Class C

"中等" Class C 条件的输入参数为：
V q = − 0.6 ; V s = 1.6 ; V k = 0 ; R L = 1.2 V_q=-0.6; V_s=1.6;V_k=0;R_L=1.2 Vq=−0.6;Vs=1.6;Vk=0;RL=1.2

在最大驱动和 −3 dB 条件下的输出如图 3.8 所示。

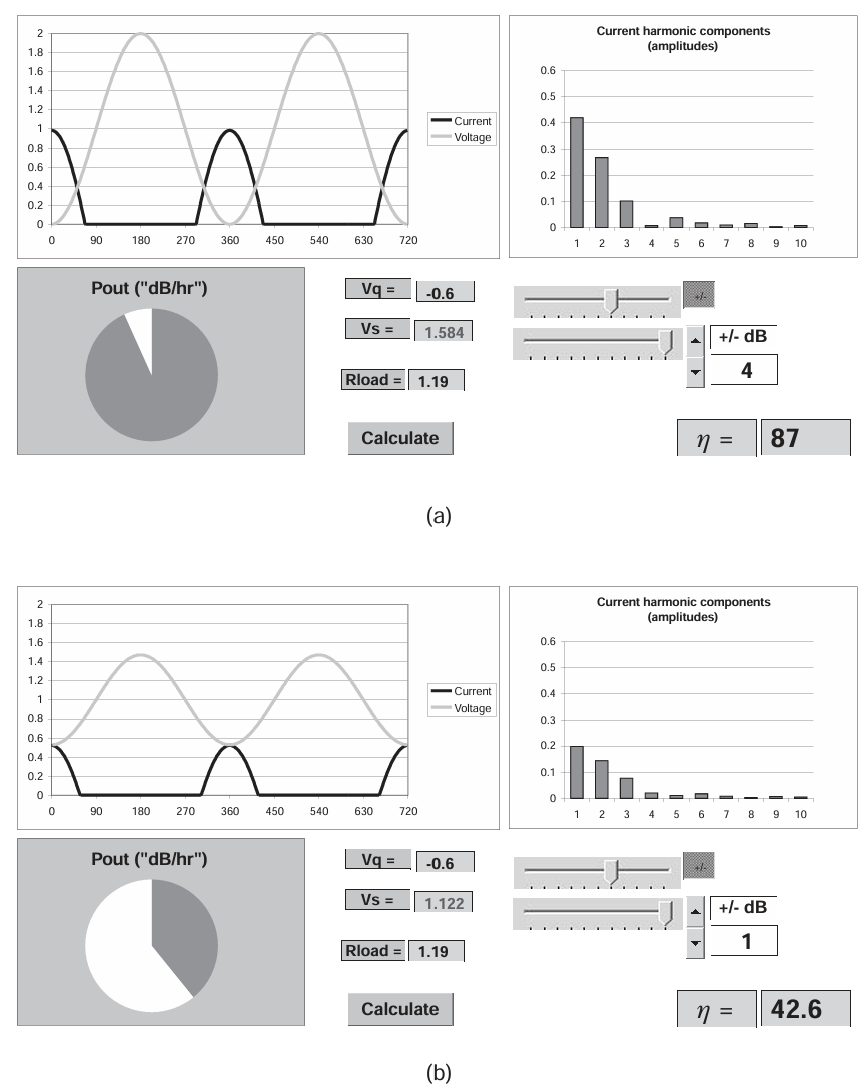
图3.8 Class C operation, V_q = −0.6: (a) full drive, and (b) 3 dB backoff.

电流波形开始呈现一系列短脉冲的形态，这些脉冲的直流分量很低，但基波 RF 分量也低于 Class AB 情况。因此，可以获得非常高的效率，但代价是 RF 输出功率降低以及输入驱动需求非常高。3 dB 降额条件下（图 3.8(b)）同样显示出高度非线性响应，并伴随较大的增益扩展。使用 Class C 模式的主要问题之一是输入电压的大幅负摆，这恰好与漏极/集电极输出电压峰值重合。这正是任何晶体管中反向击穿的最糟糕条件，即使在该周期点流过少量漏电流，也会对效率产生不利影响 。因此，加上 PUF 和功率增益迅速下降，高频和微波频率下的固态放大器中很少采用真正的 Class C 操作。目前对该模式的兴趣有所回升，主要是由于可以使用数字信号驱动 RF 功率器件。这个话题将在第 7 章和第 10 章进一步讨论。然而，图 3.9 显示了经典 Class AB 和 Class C 模式的理论功率与效率比较，以及一种概念性器件，其电流波形为矩形脉冲，而非正弦波顶帽。显然，这一概念具有一定的潜在应用价值。

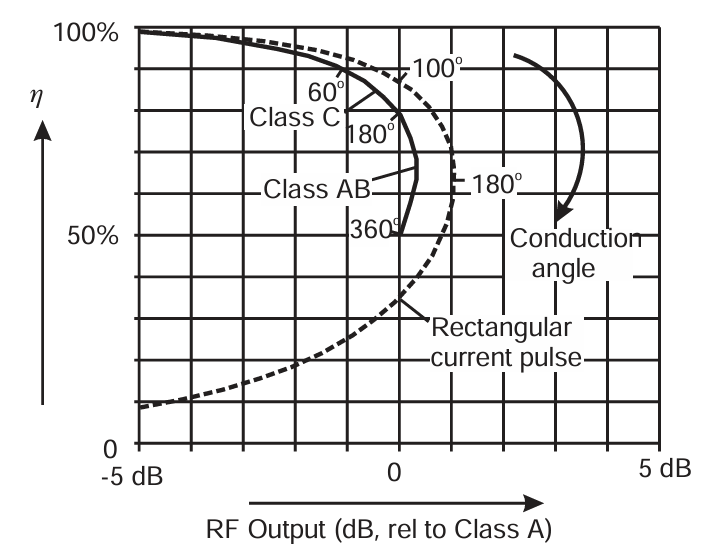
图3.9 Power/efficiency sweeps for ideal Class AB/C PAs at maximum drive (solid); equivalent plot for rectangular pulses also shown (dotted).

案例 (1) 到 (4) 及随附的 3 dB PBO 线性测试，对减少导通角模式的线性特性提供了一个较为有限的视角。图 3.10 显示了一个代表性偏置范围和 20 dB 输入功率降额范围的更广泛特性集。这些曲线是按照公式 (3.9) 至 (3.12) 计算的。使用理想 FET 模型，Class A (V_q = 0.5) 和 Class B (V_q = 0) 条件给出完全线性响应，但中间的 Class AB 设置显示出明显的增益压缩。因此可见，理想 FET 模型并非 Class AB 线性度的最优特性。这是一个重要但通常被忽略的观察。在实际中，器件的跨导在有源区通常会显示一定的增益扩展，这倾向于减小，甚至在某些情况下抵消因导通角减小造成的增益压缩。该主题将在第 4 章中更详细地讨论。

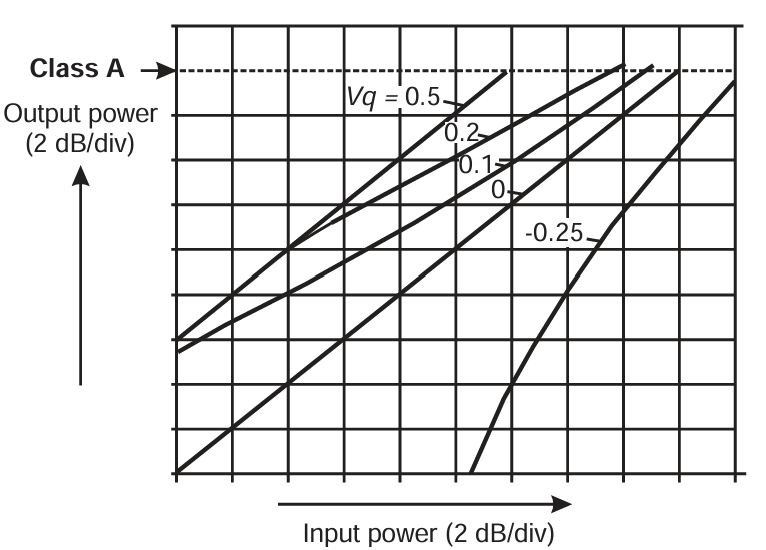
图3.10 Linearity of reduced conduction angle modes for FET model; loadline match at the peak power level and ideal output harmonic short-circuit are assumed.

图 3.11 显示了相同偏置设置下的输出功率与效率特性。Class A PBO 的效率随功率成反比下降，而 Class B 情况的效率下降与功率平方根成比例。中间情况在这两种特性之间过渡，并且最显著的是，当信号低于截断开始的水平时，特性会回到反功率规律。

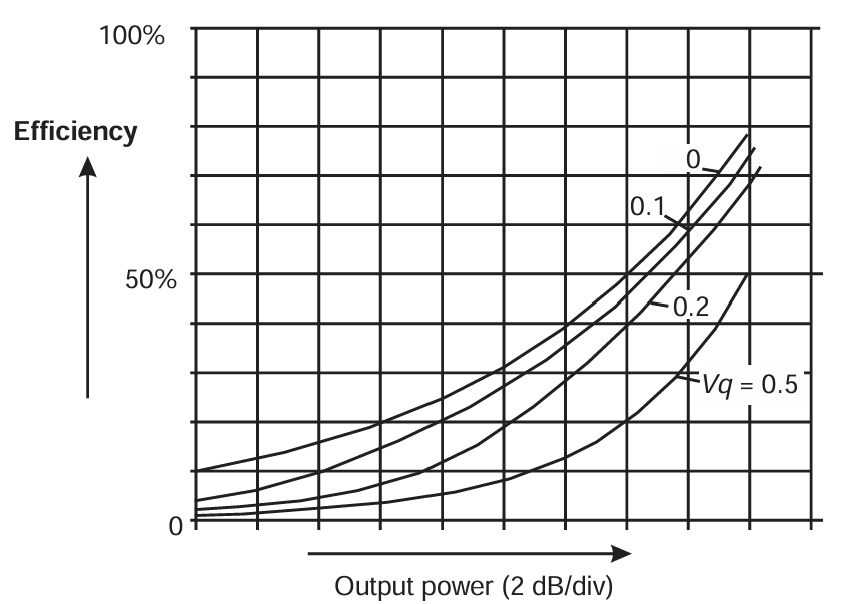
图3.11 Efficiency versus power backoff (PBO) for reduced conduction angle modes, FET model.

3.5 Reduced Conduction Angle Mode Analysis---BJT Model

到目前为止，对降低导通角模式的分析一直假设采用理想化的 FET 特性。BJT 在物理层面上是完全不同的器件，但在其上应用了类似的 Class AB/C 概念，并且经验表明可得到类似的结果。因此，本节将以与对 FET 相同的理想化思路来分析 BJT 的降低导通角模式。

虽然在模拟集成电路的线性设计中，BJT 通常被视为电流放大器，但在功率放大器分析中采用跨导模型更为合适 。如果用以下关系来表示 BJT 的输出电流
i c = I m a x e k ( v b e − 1 ) ( 3.13 ) i_c=I_{max}e^{k(v_{be}-1)}\quad(3.13) ic=Imaxek(vbe−1)(3.13)

则集电极电流 i_c 将呈现对基极-发射极电压 v_be 的指数依赖关系，这符合物理特性。k 的值可以根据需要选择，使得传输特性能够在与 FET 分析中相同的归一化输入电压尺度上绘制。图 3.12 说明了这一点，其中 k = 2 时，两种特性至少在功能上看起来相似。与 FET 器件在突然导通后表现出线性区域不同，BJT 器件的导通更为平滑，但没有这种线性区域。更高的 k 值会使导通更陡峭，但会导致更非线性的有效区域。显然，图 3.12 中绘制的三个 k 值都可能代表同一个器件，只是输入电压尺度的归一化方式不同。

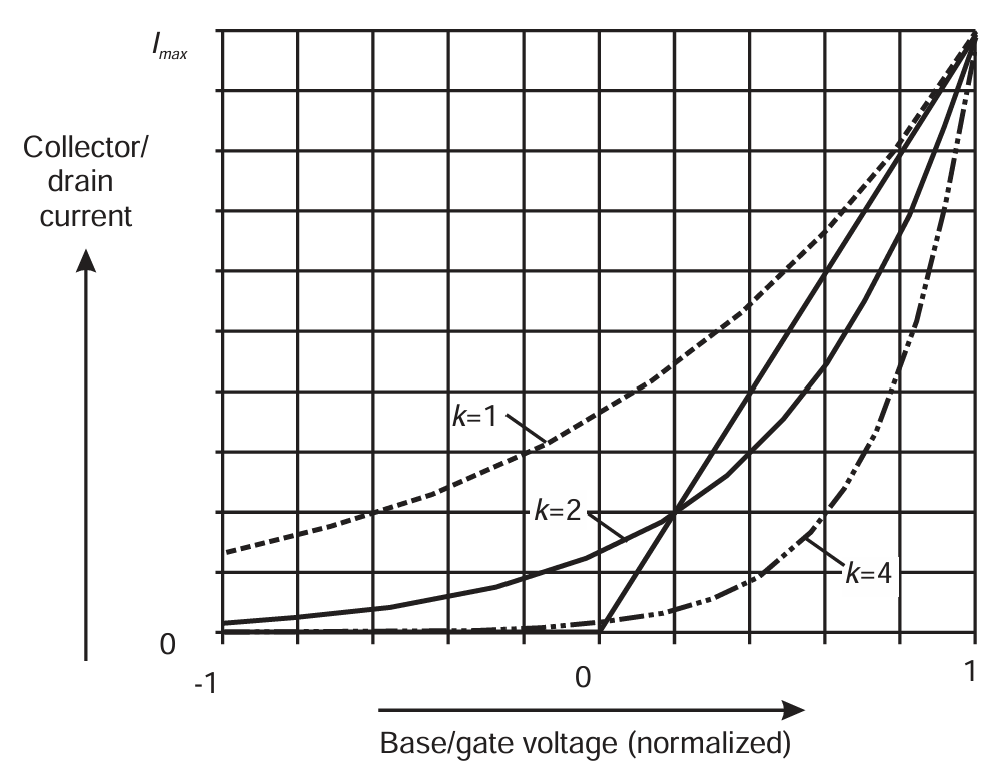
图3.12 Exponential BJT transfer characteristic, compared to ideal FET.

降低导通角模式可以通过不同的静态偏置条件以及正弦输入电压幅度来分析
v b e = V q + V s c o s ω t ( 3.14 ) v_{be}=V_q+V_scos\omega t\quad(3.14) vbe=Vq+Vscosωt(3.14)

与之前对 FET 的分析一样，静态偏置 V_q 和信号幅度 V_s 都采用从 0 到 1 的归一化尺度。其中，当 v_be =1 时，按照式 (3.13)，其对应允许的最大集电极电流 I_max 。

不幸的是，对 BJT 的 Class AB 模式进行后续分析时，其合理性比 FET 要更具疑问性，因为必须对器件输入电压 v_be 做额外的假设。对于 FET，我们到目前为止的假设是输入阻抗基本为开路，尤其是假设输入电压是外部信号的线性缩放版本 。但在 BJT 中，这个假设没那么合理，因为器件输入端对外部负载呈现的是非线性电阻 。具有讽刺意味的是，这种额外的非线性效应反而有助于改善线性度（参见第 4 章及文献 [2]），但它也带来显著复杂性。在本初步分析中将忽略这些复杂性；暂时假设 v_be 是正弦输入信号的线性缩放形式。

将 v_be 的表达式（3.10）代入式（3.9），得到
i c = I m a x e k ( V q − 1 ) ⋅ e k V s c o s θ , ( θ = ω t ) i_c=I_{max}e^{k(V_q-1)}\cdot e^{kV_scos\theta},(\theta=\omega t) ic=Imaxek(Vq−1)⋅ekVscosθ,(θ=ωt)

展开第二项指数函数，可得：
i c = I m a x e k ( V q − 1 ) [ 1 + ( k V s ) c o s θ + ( k V s ) 2 2 c o s 2 θ + ( k V s ) 3 6 c o s 3 θ + ( k V s ) 4 24 c o s 4 θ + ( k V s ) 5 120 c o s 5 θ + ... ... ] ( 3.15 ) i_c=I_{max}e^{k(V_q-1)}[1+(kV_s)cos\theta+\frac{(kV_s)^2}{2}cos^2\theta+\frac{(kV_s)^3}{6}cos^3\theta+\frac{(kV_s)^4}{24}cos^4\theta+\frac{(kV_s)^5}{120}cos^5\theta+......]\quad(3.15) ic=Imaxek(Vq−1)[1+(kVs)cosθ+2(kVs)2cos2θ+6(kVs)3cos3θ+24(kVs)4cos4θ+120(kVs)5cos5θ+......](3.15)

因此，当 kV_s 下降到低于 1 时，器件特性会变得越来越线性。当 kV_s>1 时，式 (3.15) 的高阶项将逐渐变得重要。不过，当 kV_s=2 时，可以注意到七次项的系数为 8/315，约为基波成分系数的 1%。对于图 3.12 中的 k=2，这个条件是重要的，因为它对应于 BJT 的 Class B 等效条件。

可以将式 (3.15) 中的余弦幂展开，并推导出输出电流的功率级数，包括 DC、基波和谐波成分。然而，这里将"勉为其难"地采用直接计算方式。图 3.13 展示了不同 V_q 设置下的功率传输特性。与 FET 模型（图 3.10）的对应计算相同，假设输出负载电阻在每个 V_q 的最大驱动点被选为能够实现满摆幅输出电压，并且所有谐波电压被短路。对应的功率回退（PBO）效率曲线见图 3.14。对于准 Class A 条件 V_q=V_s=0.5，线性度较好（虽然不完美），最大效率约 45%。较低静态偏置设置会在高驱动区呈现逐渐增强的增益扩展特性。准 Class B 条件 V_q=0,V_s=1 的效率峰值为 70%，并在最高 6 dB 功率范围内出现约 4 dB 的增益扩展。

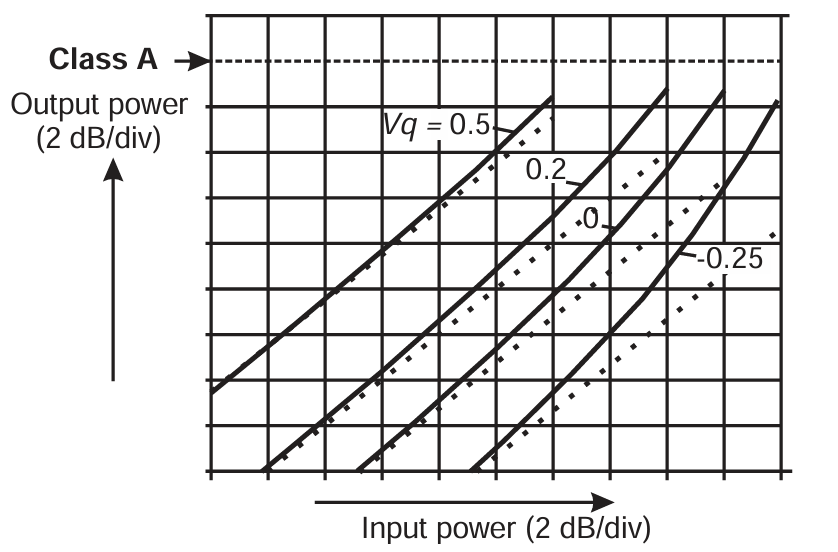
图3.13 BJT Class AB power transfer characteristics (same scales and equivalent normalization as in the FET case, Figure 3.10).

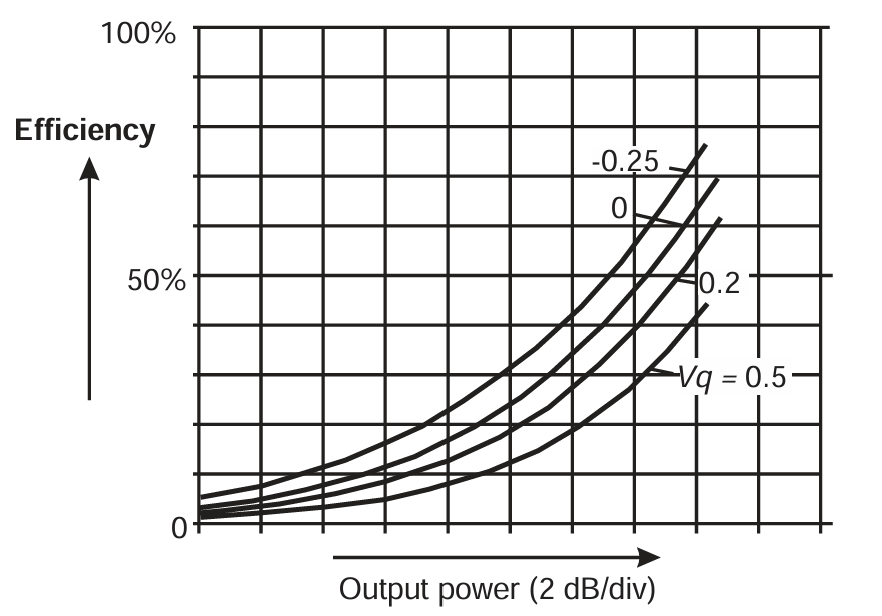
图3.14 BJT Class AB efficiency versus output power (compare with equivalent FET plot, Figure 3.11).

尽管这些结果在总体趋势上与对应的 FET 计算"看起来类似"，但仍存在一些明显差异。尤其是，BJT 的指数特性会导致当静态偏置降低时，小信号增益显著下降；而更低的静态偏置条件则表现出令人不安的明显增益扩展 。将在第 4 章（参考文献 [2]）中展示，如果考虑输入端匹配网络与基--射极结非线性阻抗之间的相互作用，BJT 可以获得更为线性的响应。这一点也印证了一个普遍观察：BJT（尤其是 GHz 级的现代衍生器件 HBT）在可变包络信号的线性度与效率折衷方面，往往优于 FET。无论如何，可以指出的是增益扩展比增益压缩要更容易线性化补偿。在实际设计中存在许多不同的机制，它们几乎不可避免地会在 Class AB BJT 功率放大器中引入某些抵消或抵减效应，从而改善互调失真或邻道功率响应。

3.6 Effect of I-V "Knee"

前述分析现在可扩展，用来考察更真实的"拐点电压"对结果的影响。对于 FET 和 BJT，这些影响都非常类似。在晶体管放大器中，knee 电压通常占 DC 电源电压相当大的百分比；在便携式电池供电的 PA 应用中，knee 电压的影响甚至可能主导整个设计思路。

图 3.15 显示了一个经过修改的"理想 FET" I--V 特性，其中加入了更真实的导通区域。参数 V_k 是归一化到 DC 电源电压 V_dc 的 knee 电压，晶体管电流被修改为：
I d = v g ⋅ g m ⋅ I m a x ( 1 − e − ( v d s V k ) ) ( 3.16 ) I_d=v_g\cdot g_m\cdot I_{max}(1-e^{-(\frac{v_{ds}}{V_k})})\quad(3.16) Id=vg⋅gm⋅Imax(1−e−(Vkvds))(3.16)

其中 v_ds 是漏--源（输出）电压，也归一化到 V_dc。

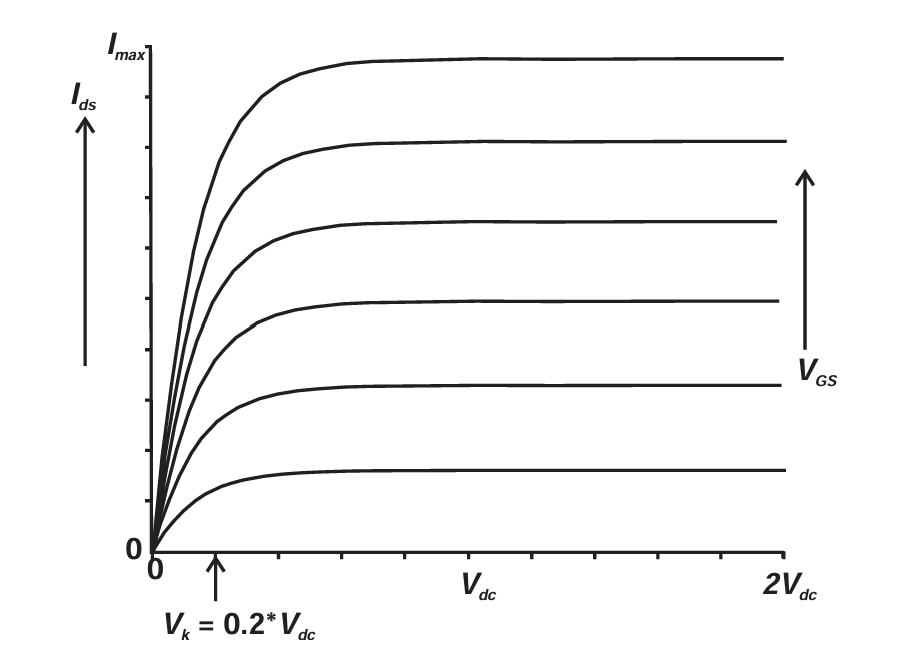
图3.15 Knee region modification to ideal I-V characteristics.

当 v_ds = V_k 时，
I d = v g ⋅ g m ⋅ I m a x ⋅ ( 1 − e − 1 ) I_d=v_g\cdot g_m\cdot I_{max}\cdot(1-e^{-1}) Id=vg⋅gm⋅Imax⋅(1−e−1)

因此在 knee 电压处的电流将会下降至其高电压饱和值的大约 63%。如果 V_k 归一化到电源电压，取值为 0.1 对许多实际器件来说是合理的。例如在 5 V 电源下工作的 MESFET 或 BJT，或者在 24 V 电源下 knee 为 4 V 的 LDMOS。

由于此时的器件电流同时依赖输入与输出电压，输出电压预测变成一个"递归求解问题"。为了避免这种难度，可以直接指定输出电压摆幅，然后用跨导关系乘以漏电压依赖项（式 3.16）来计算电流。输出电压幅度参数 V_out 也归一化到 V_dc。

比如一个Class B 放大器，V_q = 0，V_s = 1.0，V_k = 0.1，V_out = 1.0。

这些条件下的波形如图 3.16(a)。应与理想（无 knee）Class B 情况（图 3.7）直接对比。最显著的特征是电流波形出现了明显的"双峰"结构。这是因为漏电压会下降到接近 0 的必然结果。虽然这种双峰脉冲的 DC 分量依然较低，但 RF 输出功率比理想情况降低超过 2 dB。不过效率仍保持在 70% 左右。

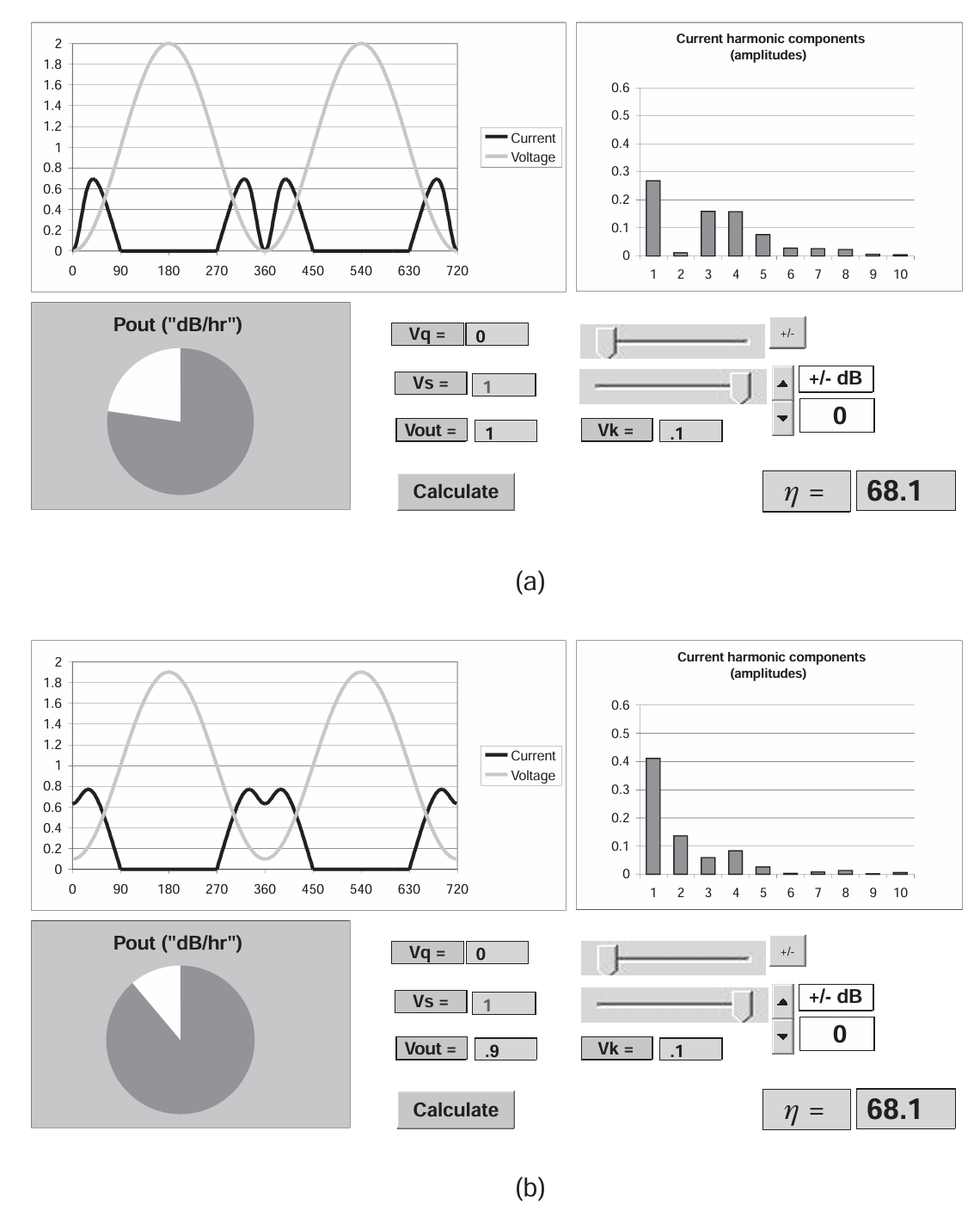
图3.16 Class B operation with I-V knee effects included: (a) full output RF voltage swing, and (b) swing reduced by 10%.

这代表着 RF 功率以及 PUF发生了重大损失。显然恢复性能的第一步，就是减少输出电压摆幅，使电流不再跌到 0。图 3.16(b) 展示了以下参数下的结果：
V q = 0 ; V s = 1.0 ; V k = 0.1 ; V o u t = 0.9 V_q=0;V_s=1.0;V_k=0.1;V_{out}=0.9 Vq=0;Vs=1.0;Vk=0.1;Vout=0.9

RF 输出功率恢复到距离理想值 仅 1 dB，并且效率也幸运地保持相同的水平。进一步实验 V_out 参数显示此处条件接近最优：仅比理想损失 1 dB 功率，效率下降不到 10%。（再继续减小 V_out，RF 功率仅略有提高，但效率显著下降。）更具讽刺意味或巧合的是，此时计算出的最佳输出负载电阻约为 0.98，几乎与理想模型预测值完全一致。这种"模型中不同的理想化假设相互抵消彼此的不利影响"的情况并不罕见，也为这种类型的建模分析提供了强有力的支持。

3.7 Input Drive Requirements

在此前对传统高效率工作模式的讨论中，多次强调过一个重要缺点，它们所需的驱动电平比使用同一器件的线性 Class A 放大器要高得多，可以高出 6 dB。这一点在更高的射频频率下尤其麻烦，因为超过 10 dB 的线性增益常常是一种奢侈品。若要获得更高增益，则需要付出昂贵的器件技术或封装成本。因此，在 10 GHz 以上的大多数功率放大器实际上都采用 Class A 工作模式，正是出于这个原因。

如 3.3 节提到的，实验证据表明双极型晶体管，以及程度较小的 FET，其 Class A 与 Class B 的功率增益差异并没有理论分析那么大。从某种角度看，BJT 似乎天生适合 Class B 工作：在零基极偏置时，大幅度射频驱动信号会自然地使正向二极管导通与关断，集电极电流也随之开关。关键在于输入阻抗在整个射频周期中发生显著变化，因此 Class B 所需的额外射频驱动功率并不能简单预测。与此相反，FET 更自然地表现为线性放大器，在正弦驱动下需要靠截止特性完成大部分波形塑形；其栅极阻抗在整个射频周期中基本保持常数（除去由耗尽电容引起的一些小变化）。因此，额外的 6 dB 驱动需求几乎无法避免，这也可能成为 FET 相比 BJT 的一个显著劣势。

基于效率与功率增益的理想化结果，图 3.17 定量展示了高频高效率 PA 设计中的问题------可用增益可能轻易掉到 10 dB 以下。例如，对于一个输出效率为75%、功率增益为6 dB（对应线性增益约 12 dB） 的 Class B 功放。如果其前驱动级效率为 50%，那么整体效率只有 55%。在这种情况下，功放的效率与增益之间必须权衡。从系统角度看，更合理的方式可能是将功放工作在中度 AB 状态，使其功率增益比 Class B 高约 3 dB。例如65%的 PA 效率下可以达到9 dB 的功率增益，此时两级总体效率约为 57%。虽然整体效率提升并不显著，但这说明如果功率增益明显下降，则再追求超高效率的 PA 并无太大意义 。

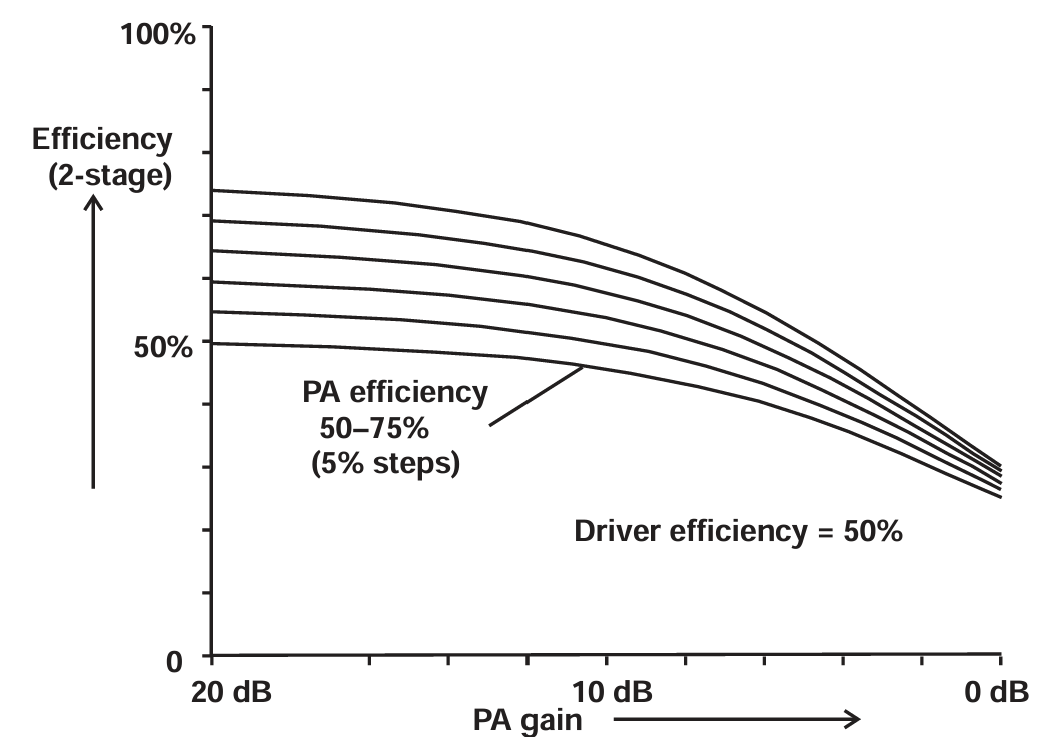
图3.17 Effect of PA gain and drive power on overall system efficiency.

在多级放大器链中，PA 级的驱动信号可能并非正弦波。事实上，可以通过调制驱动信号的波形（特别是其二次谐波成分）来缓解 Class AB 或 Class B 的驱动需求。图 3.18 显示了一个典型、几乎最优的情况：如果驱动级能够让 PA 输入处产生类似 Class B 的波形，那么就可以获得 Class B 的全部传统优点，而不必承受过高的驱动功率。实际上，图 3.18 中波形经整形后的基波成分，与在 Class A 操作中在相同电压范围摆动的正弦波完全相同。因此就基波功率增益而言，该 PA 与 Class A 相同；就效率而言，它又具备 Class B 的效率 。此外，由于 PA 晶体管只在其线性区域内工作，并且大幅负向摆幅被消除，这种方式甚至可能允许器件使用比传统过驱方式更高的供电电压 。

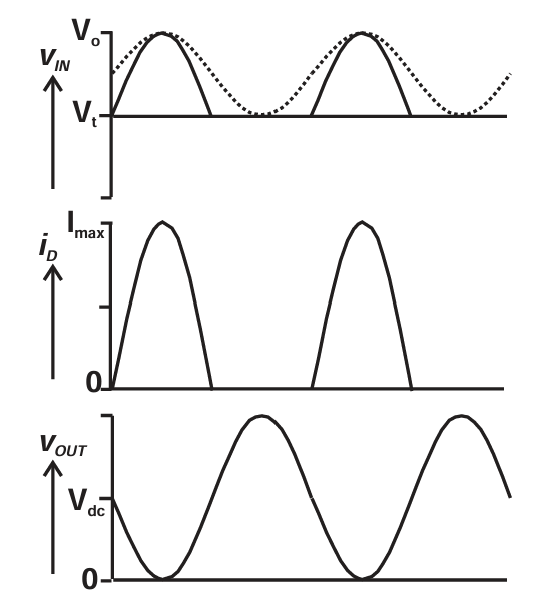
图3.18 Class B operation with a wave-shaped RF drive signal. Fundamental component of drive signal (dotted) is half of the amplitude required if drive signal were sinusoidal.

生成这种整形驱动波形需要产生足够的二次谐波成分，可通过驱动级的非线性操作，或从 PA 输出端反馈部分二次谐波来实现。甚至可能利用输入结的非线性 C--V 特性 来产生有利的波形整形（见参考文献 [3]，并将在第 4 章进一步讨论）。需要注意的是如果二次谐波相位设置不当，反而会导致效率下降 。通过中间级匹配网络的频率响应，还可以进一步调整谐波的混合比例。图 3.19 展示了一种可能的实现方式驱动级可采用"倒置 Class B "工作方式，即器件偏置接近饱和区，负向的 RF 驱动使电流在小于半周期的时间内降至零。如果驱动器输出负载呈现足够宽带的电阻性，其输出电压波形将正是驱动 Class B PA 所需要的那种（见图 3.19©）。

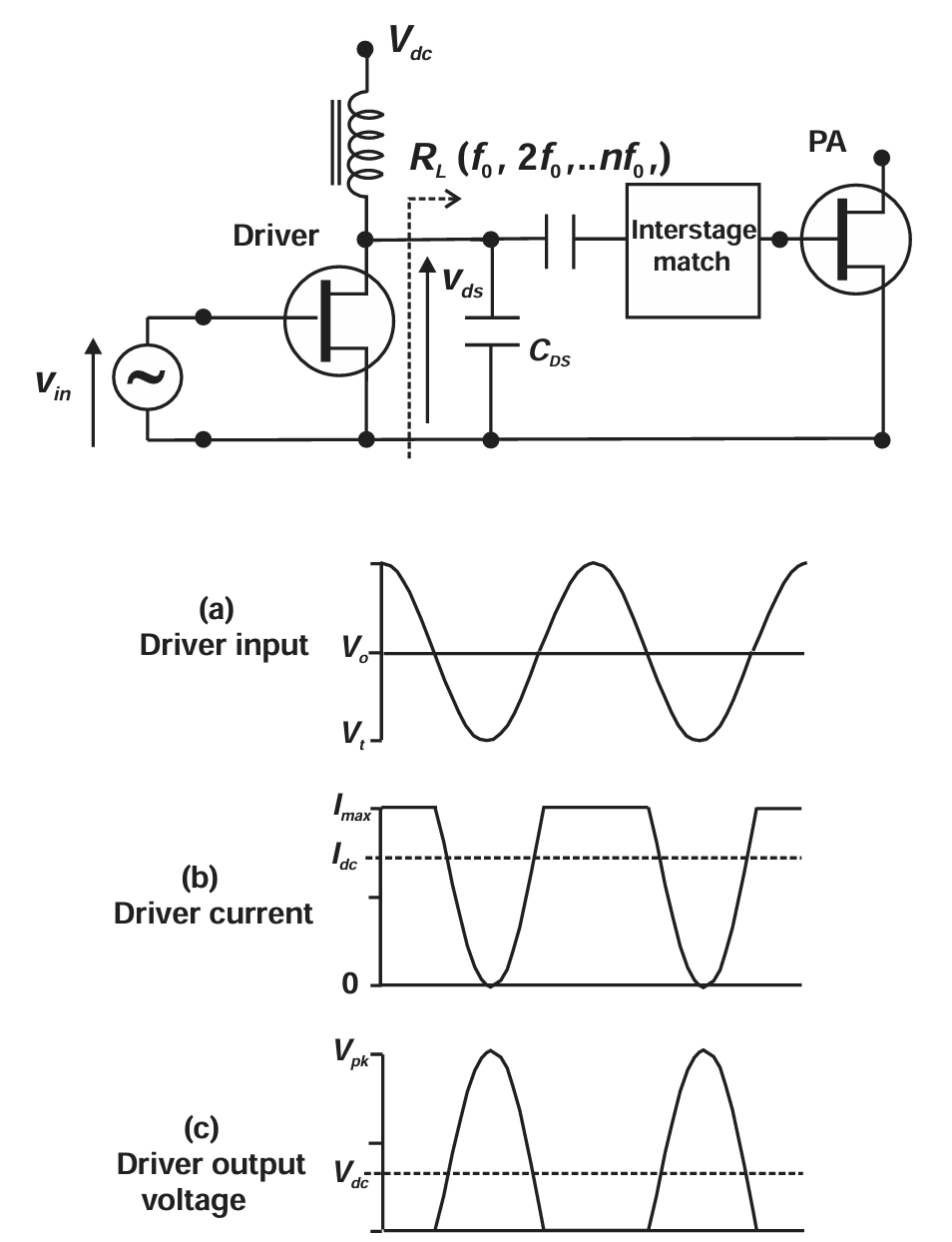
图3.19 Voltage and current waveforms for possible PA driver stage, producing a suitably wave-shaped output voltage for a Class B PA input.

这种放大器的效率通常较低，因为电流波形并非最佳。图 3.19 所示驱动放大器的效率可以做如下简单估计：

• 当前波形：反向半波整流余弦波，峰值I_max，基波分量幅值I₁=I_max/2，直流分量I_dc=（1-1/ π \pi π）·I_max
• 电压波形：半波整流余弦波，峰值电流I_max（B类波形），峰值电压V_pk= π \pi π·V_dc，基波分量幅值V₁= π \pi π·V_dc/2.
• 所以基波射频功率=(V₁·I₁)/2=(I_max· π \pi π·V_dc)/8，直流功率=V_dc·(1-1/ π \pi π)·I_max，效率=( π \pi π/8)/(1-(1/ π \pi π))=57.6%

这是一个对驱动级来说可以接受的效率。不幸的是，PA 晶体管的输入并不会表现为宽带电阻，因此需要设计一个宽带的级间匹配网络，将 PA 级的输入阻抗变换为所需的电阻负载.图 3.19 的波形都是在假设这一点的基础上给出的。这样的网络在实际中是可行的，尤其当匹配仅在谐波频率上需要达到要求，而不是在连续频带范围内时。

正如本节开头所指出的，这是一个值得进一步研究的高级主题，而本节内容并不能构成一个完整的解决方案。然而可以推测，这种条件（或某种弱化版本）在实际中被使用的频率远高于其被有意识设计的频率。在多级 PA 中，通过对偏置和级间匹配进行适当调谐，通常会观察到复杂的行为，其在功率、线性度和效率之间的权衡似乎与调谐输出匹配时获得的情况一样突出。本质上来说，几乎任何在 PA 级驱动信号中引入的二次谐波，只要相位适当，都可以降低实现高效率模式所需的表观过驱动量，而这无疑在许多实际情形中都会成为一个影响因素。

3.8 Conclusions

本章介绍了传统的缩短导通角模式，并重点利用理想化的数学模型进行了定量分析。对经典的 A、AB、B 和 C 类模式进行了详细分析，并分别量化了有限拐点电压以及线性区弱非线性效应对 FET 和 BJT 模型的影响。同时，本章也研究了 PA 增益对整体效率的影响，并讨论了可能存在的折衷关系。最后，提出了一些通过驱动信号波形整形来改善多级 PA 性能的可能方法。

本章的大部分分析均采用了输出负载谐波短路的传统假设。这在实际实现高效率射频放大器中是一个非常重要的问题，并将在下一章中进行更为详细的讨论。

参考文献

1\] Doherty, W. H., "A New High Efficiency Power Amplifier for Modulated Waves," Proc. IRE, Vol. 24, No. 9, September 1936, pp. 1163--1182. \[2\] Cripps, S. C., Advanced Techniques in RF Power Amplifier Design, Norwood, MA: Artech House, 2002. \[3\] White, P. M., "Effect of Input Harmonic Termination on High Efficiency Class B and Class F Operation of PHEMT Devices," Proc. IEEE Intl. Microw. Symp., MTT-S 1998, THIF-05.