
通过两种阈值方法的对比,可观察小波变化去噪在混合非高斯噪声环境下的鲁棒去噪效果。程序还绘制了时域波形、细节系数图及功率谱密度对比,为工程应用提供直观结果。
原创程序,非AI生成,请勿翻卖。截图为真实运行结果,包运行成功
文章目录
程序简介
本文所述的例程构建了包含多频率的真实测试信号,并在其上叠加拉普拉斯噪声、脉冲噪声与高斯噪声的混合非高斯扰动,用于验证小波变换在复杂噪声环境下的去噪性能。程序首先对含噪信号进行多层小波分解,获得每一层的近似系数与细节系数,然后分别实现两类针对非高斯噪声的阈值化处理方法
阈值化后的细节系数配合最深层近似系数重构信号,并分别计算重构前后的 SNR 与 RMSE,用于定量评估去噪效果。最后,代码给出了时域波形、SWT 系数矩阵以及功率谱密度的对比图,以展示不同阈值策略在处理非高斯噪声时的表现差异。
运行结果
真实信号、含噪信号、去噪后的信号曲线:
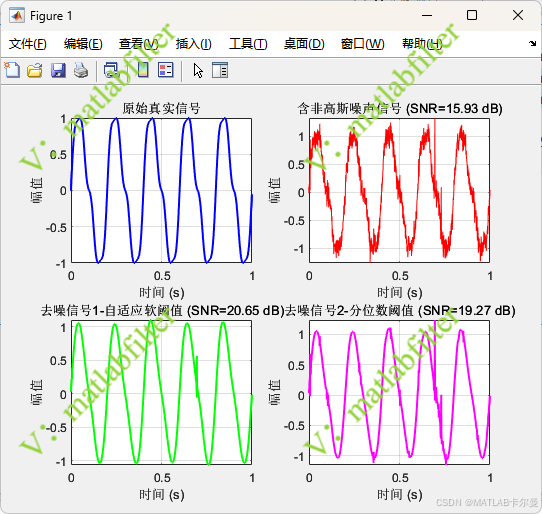
细节系数矩阵:
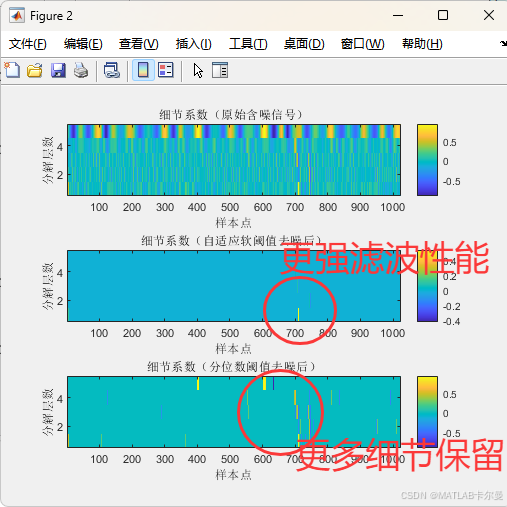
功率谱密度:
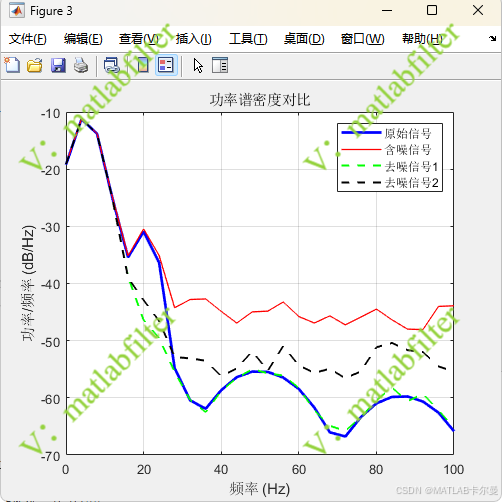
命令行7输出:

MATLAB源代码
完整代码如下:
matlab
%% 小波变换:非高斯噪声去噪
% 作者:matlabfilter
% 2025-12-09/Ver1
clear; close all; clc;
%% 生成含非高斯噪声的测试信号
fs = 1024; % 采样频率
t = 0:1/fs:1-1/fs; % 时间向量(长度1024=2^10)
N = length(t);
% 原始信号:多频率成分
f1 = 5; f2 = 10; f3 = 20;
signal_clean = sin(2*pi*f1*t) + 0.2*sin(2*pi*f2*t) + 0.1*sin(2*pi*f3*t);
% 添加非高斯噪声
% 类型1:拉普拉斯噪声(尖峰分布)
laplace_noise = laprnd(1, N, 0, 0.01);
% 类型2:脉冲噪声(椒盐噪声)
impulse_noise = zeros(1, N);
impulse_idx = randperm(N, round(0.01*N)); % 1%的位置
impulse_noise(impulse_idx) = randn(1, length(impulse_idx)) * 0.5;
% 类型3:混合噪声 同时添加高斯噪声
mixed_noise = laplace_noise + impulse_noise + 0.1*randn(1, N);
% 含噪信号
signal_noisy = signal_clean + mixed_noise*1;
%% SWT分解
level = 5; % 分解层数
wname = 'db4'; % 小波基完整代码下载链接:
https://download.csdn.net/download/callmeup/92445555
或:
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者