文章目录
- [一. 力扣 [53. 最大子数组和](https://leetcode.cn/problems/maximum-subarray/description/)](#一. 力扣 53. 最大子数组和)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [二. 力扣 [918. 环形子数组的最大和](https://leetcode.cn/problems/maximum-sum-circular-subarray/description/)](#二. 力扣 918. 环形子数组的最大和)
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [三. 力扣 [152. 乘积最大子数组](https://leetcode.cn/problems/maximum-product-subarray/description/)](#三. 力扣 152. 乘积最大子数组)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [四. 力扣 [1567. 乘积为正数的最长子数组长度](https://leetcode.cn/problems/maximum-length-of-subarray-with-positive-product/description/)](#四. 力扣 1567. 乘积为正数的最长子数组长度)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [五. 力扣 [413. 等差数列划分](https://leetcode.cn/problems/arithmetic-slices/description/)](#五. 力扣 413. 等差数列划分)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [六. 力扣 [978. 最长湍流子数组](https://leetcode.cn/problems/longest-turbulent-subarray/description/)](#六. 力扣 978. 最长湍流子数组)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [七. 力扣 [139. 单词拆分](https://leetcode.cn/problems/word-break/description/)](#七. 力扣 139. 单词拆分)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
- [八. 力扣 [467. 环绕字符串中唯一的子字符串](https://leetcode.cn/problems/unique-substrings-in-wraparound-string/description/)](#八. 力扣 467. 环绕字符串中唯一的子字符串)
-
- [1. 题目解析](#1. 题目解析)
- [2. 算法原理](#2. 算法原理)
- [3. 代码](#3. 代码)
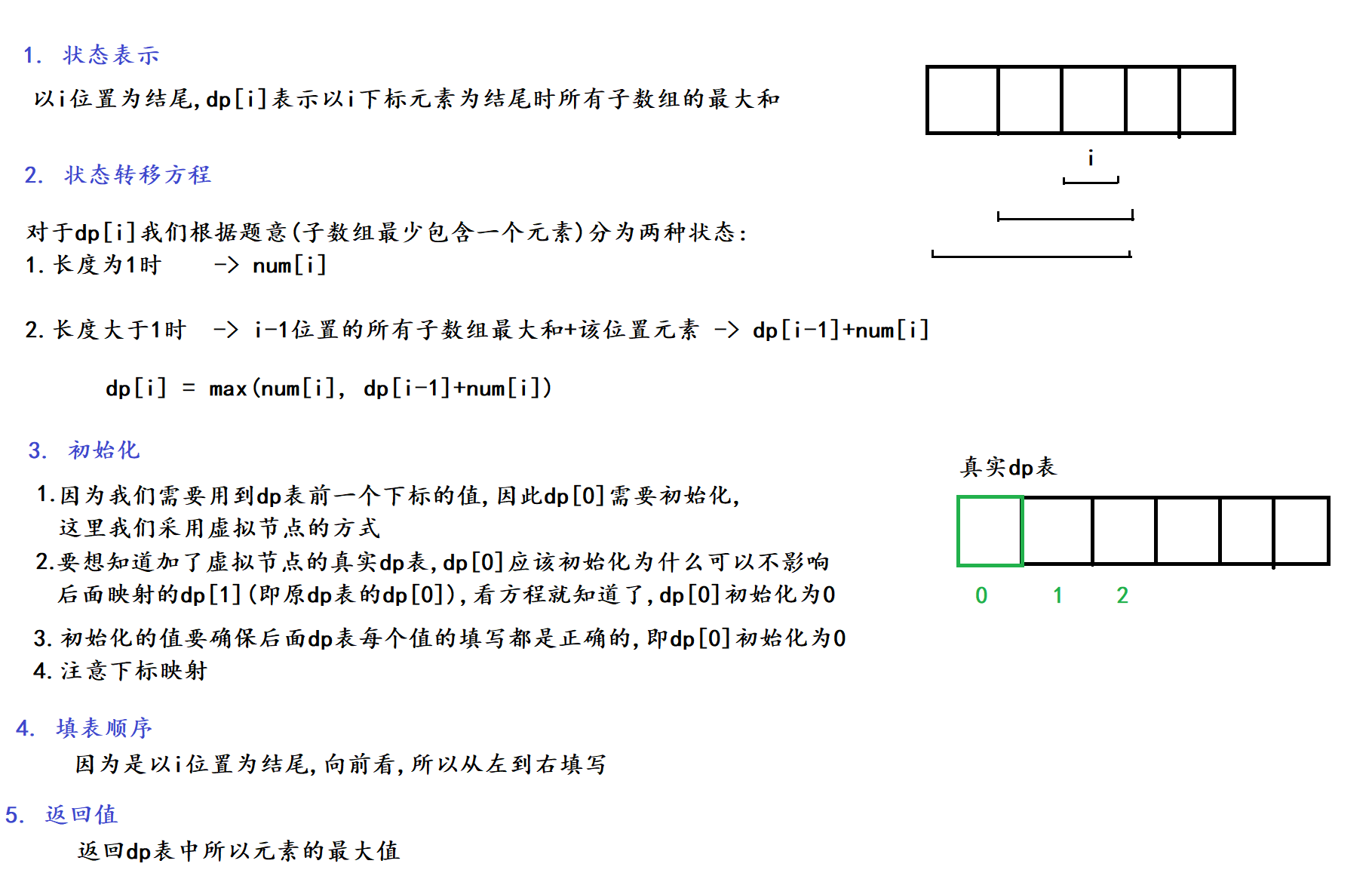
一. 力扣 53. 最大子数组和
1. 题目解析
这道题的题目非常简短, 也很好理解, 这里不过多赘述
2. 算法原理
每一步注意点和细节都写在了图解里~
3. 代码
java
public int maxSubArray(int[] nums) {
// 建dp表, 初始化dp
int n = nums.length;
int[] dp = new int[n + 1];
// 填写dp表, 边填表边求最大值
int ret = -0x3f3f3f3f;
for (int i = 1; i <= n; i++) {
dp[i] = Math.max(nums[i - 1], dp[i - 1] + nums[i - 1]);
ret = Math.max(ret, dp[i]);
}
return ret;
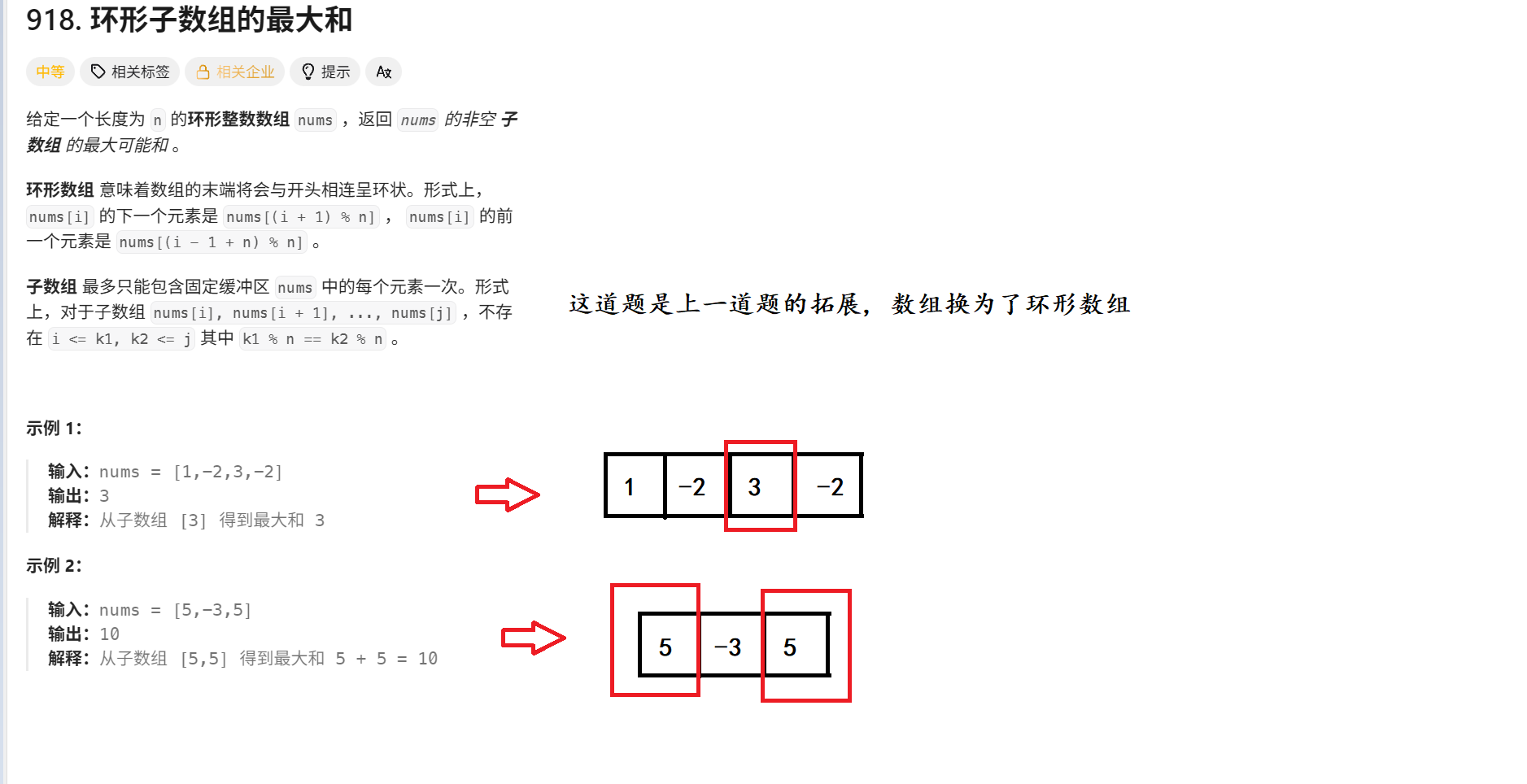
}二. 力扣 918. 环形子数组的最大和
1. 题目解析
这道题可以理解为上一道题的进阶版本, 题意不难理解
2. 算法原理
所有注意点都标记在了图解里, 保姆级教学~
3. 代码
java
public int maxSubarraySumCircular(int[] nums) {
// 创建和初始化dp表
int n = nums.length;
int[] f = new int[n + 1];
int[] g = new int[n + 1];
int sum = 0;
// 填写dp表
int fmax = -0x3f3f3f3f;
int gmin = 0x3f3f3f3f;
for (int i = 1; i <= n; i++) {
sum += nums[i - 1];
f[i] = Math.max(nums[i - 1], f[i - 1] + nums[i - 1]);
fmax = Math.max(fmax, f[i]);
g[i] = Math.min(nums[i - 1], g[i - 1] + nums[i - 1]);
gmin = Math.min(gmin, g[i]);
}
return gmin == sum ? fmax : Math.max(fmax, sum - gmin);
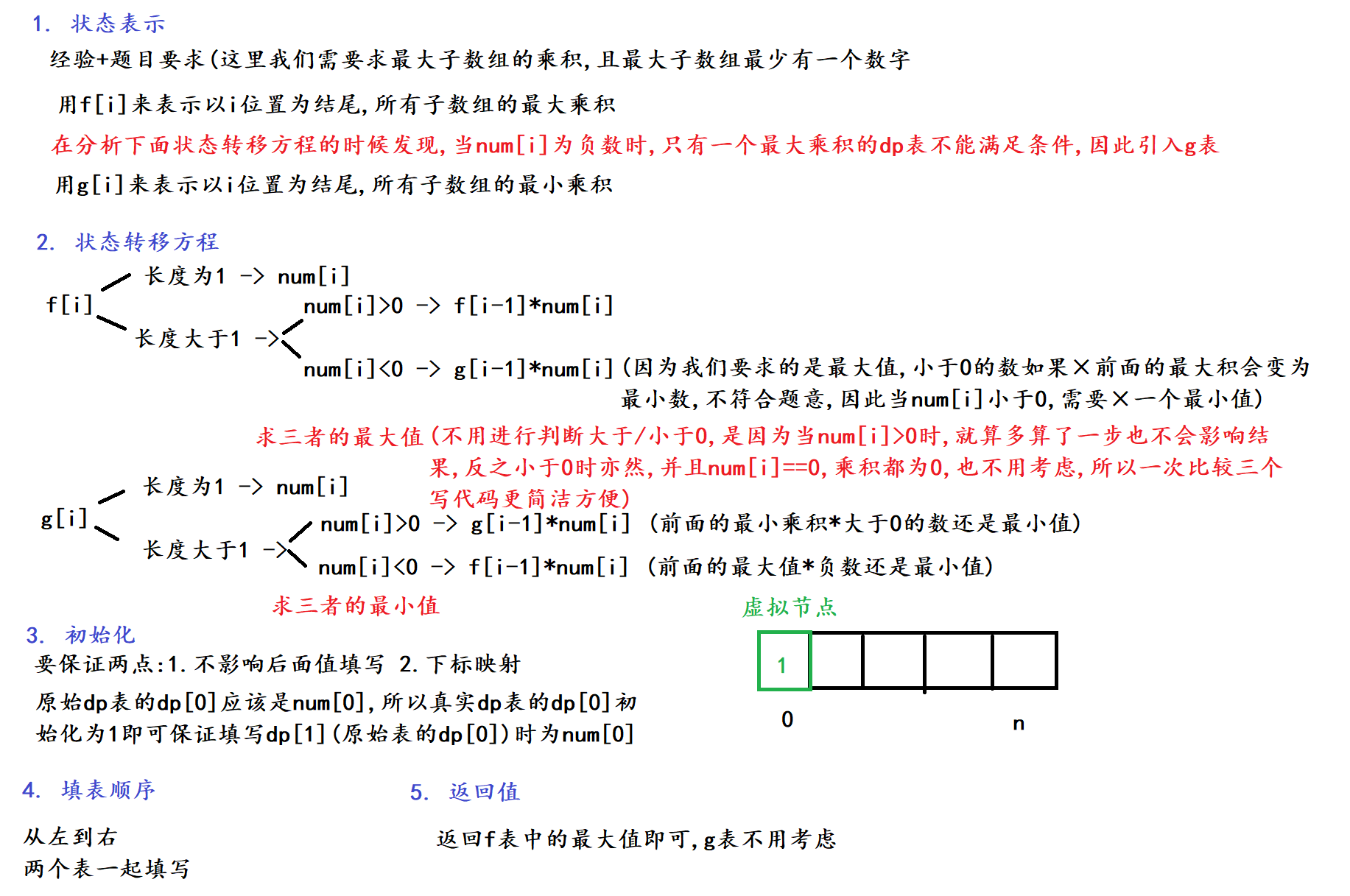
}三. 力扣 152. 乘积最大子数组
1. 题目解析
这道题和第一道题十分相似, 最大和变为了最大乘积, 但本质没变
2. 算法原理
不多哔哔, 直接上图, 原因/做法都已标明
3. 代码
java
public int maxProduct(int[] nums) {
// 创建dp表
int n = nums.length;
int[] f = new int[n + 1];
int[] g = new int[n + 1];
// 初始化dp表
f[0] = g[0] = 1;
int ret = -0x3f3f3f3f;
// 填表
for (int i = 1; i <= n; i++) {
int t = nums[i - 1];
f[i] = Math.max(t, Math.max(f[i - 1] * t, g[i - 1] * t));
g[i] = Math.min(t, Math.min(g[i - 1] * t, f[i - 1] * t));
ret = Math.max(f[i], ret);
}
return ret;
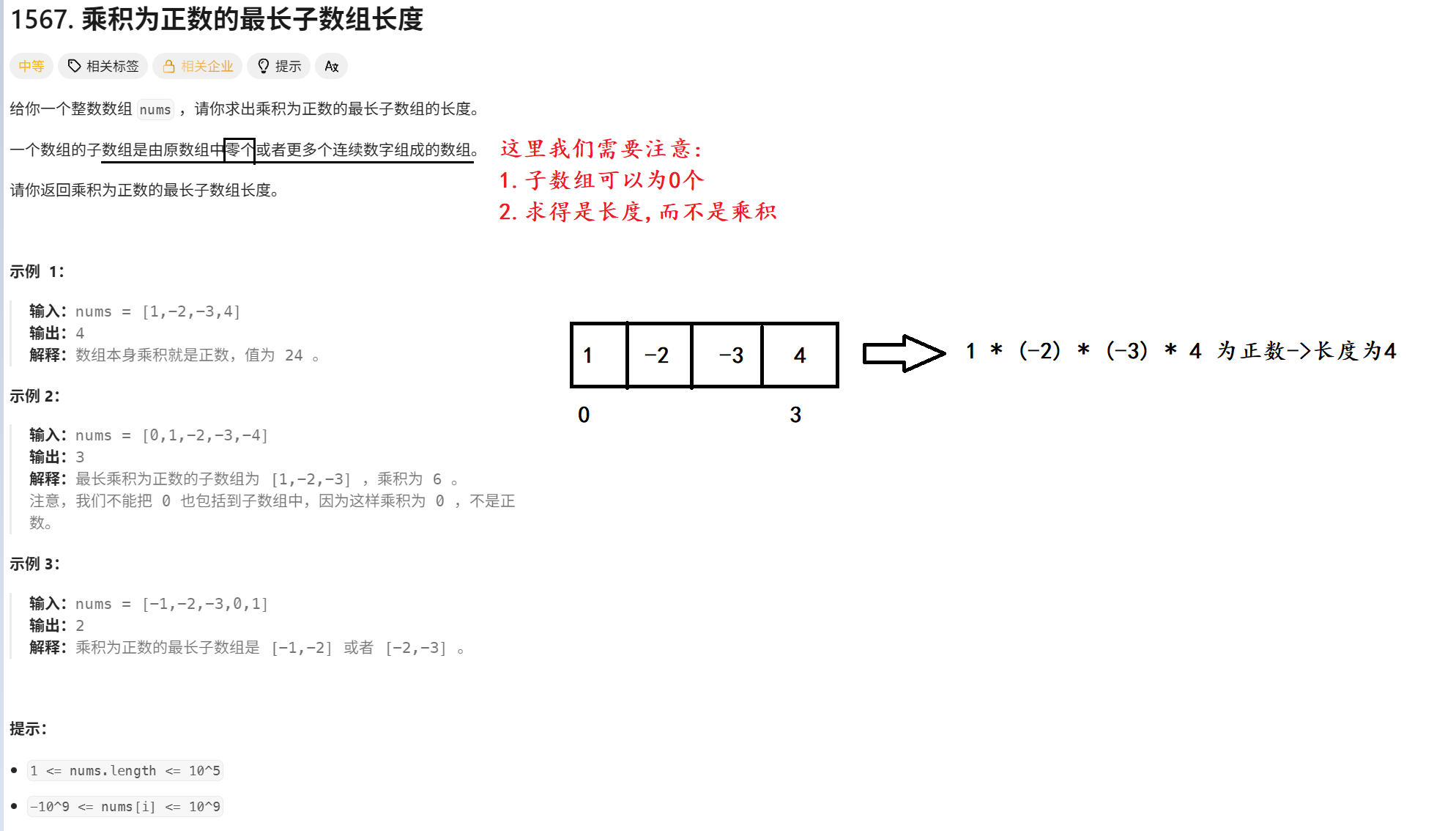
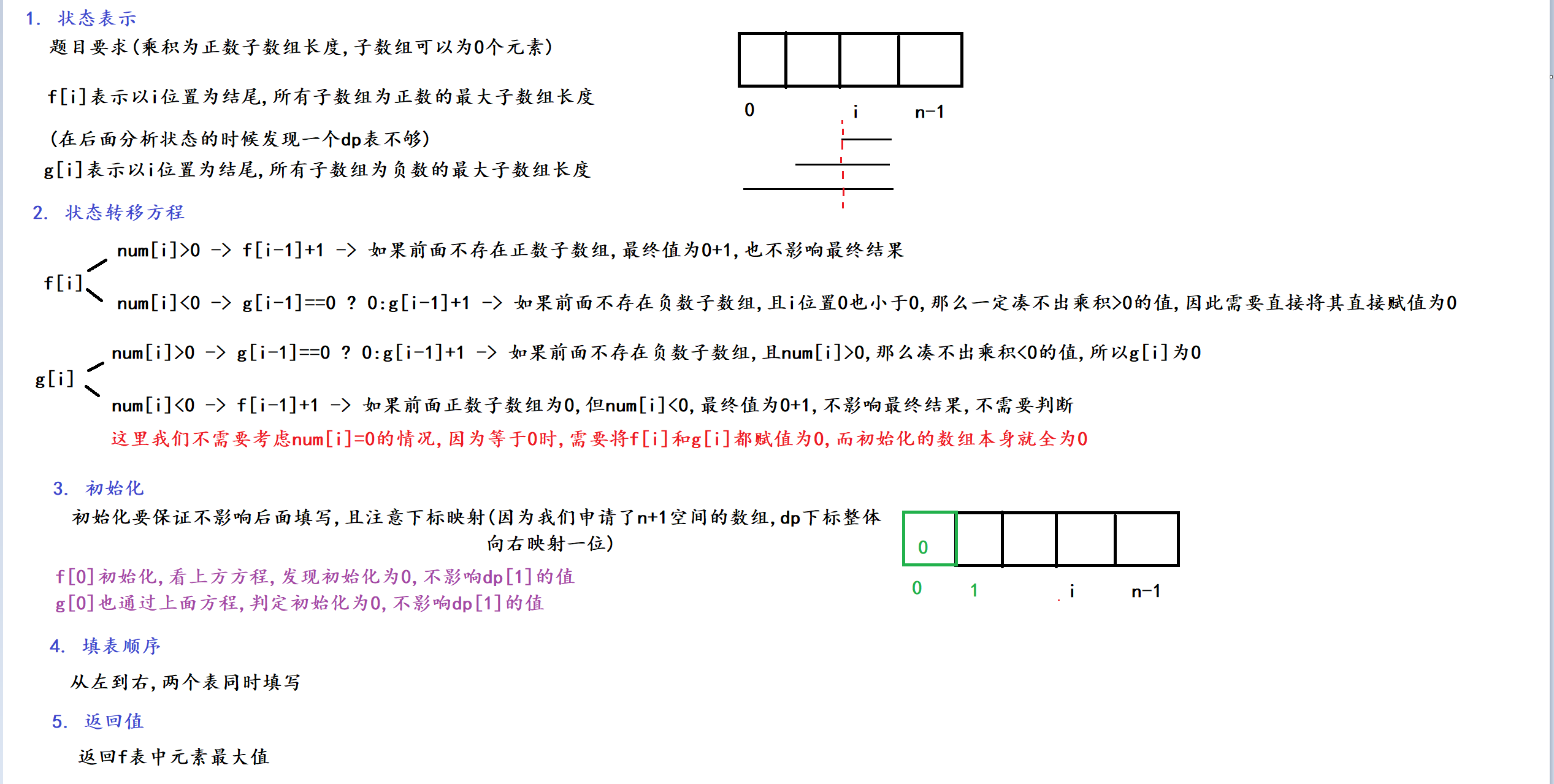
}四. 力扣 1567. 乘积为正数的最长子数组长度
1. 题目解析
有一些新题目要求, 下面都已经点出
2. 算法原理
需要注意的点较多, 但答题思路一致
3. 代码
java
public int getMaxLen(int[] nums) {
int n = nums.length;
int[] f = new int[n + 1];
int[] g = new int[n + 1];
int ret = 0;
for (int i = 1; i <= n; i++) {
int t = nums[i - 1];
if (t > 0) {
f[i] = f[i - 1] + 1;
g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
}else if (t < 0) {
f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
g[i] = f[i - 1] + 1;
}
ret = Math.max(ret, f[i]);
}
return ret;
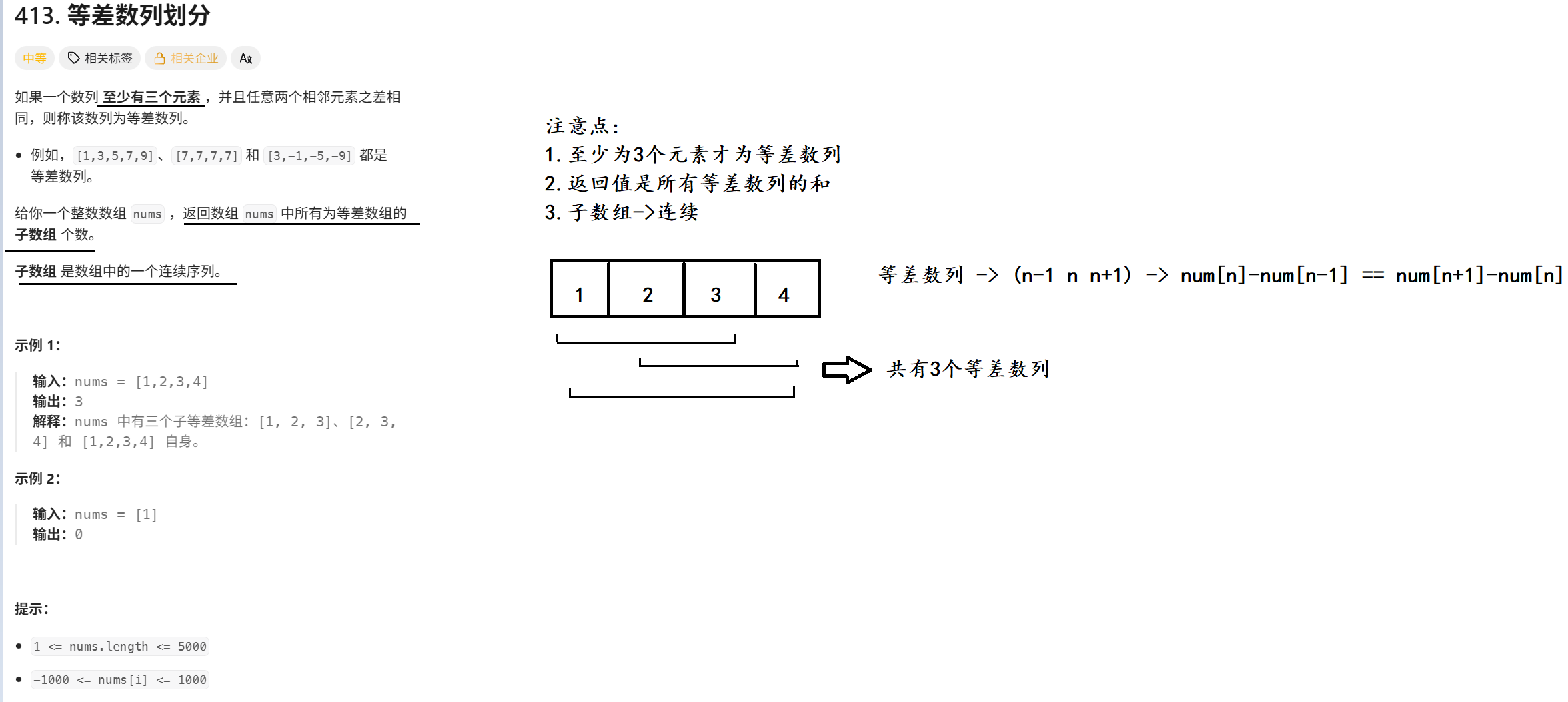
}五. 力扣 413. 等差数列划分
1. 题目解析
注意点都写在了下面图解
2. 算法原理
3. 代码
java
public int numberOfArithmeticSlices(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
int ret = 0;
for (int i = 2; i < n; i++) {
dp[i] = nums[i - 1] - nums[i - 2] == nums[i] - nums[i - 1] ? dp[i - 1] + 1 : 0;
ret += dp[i];
}
return ret;
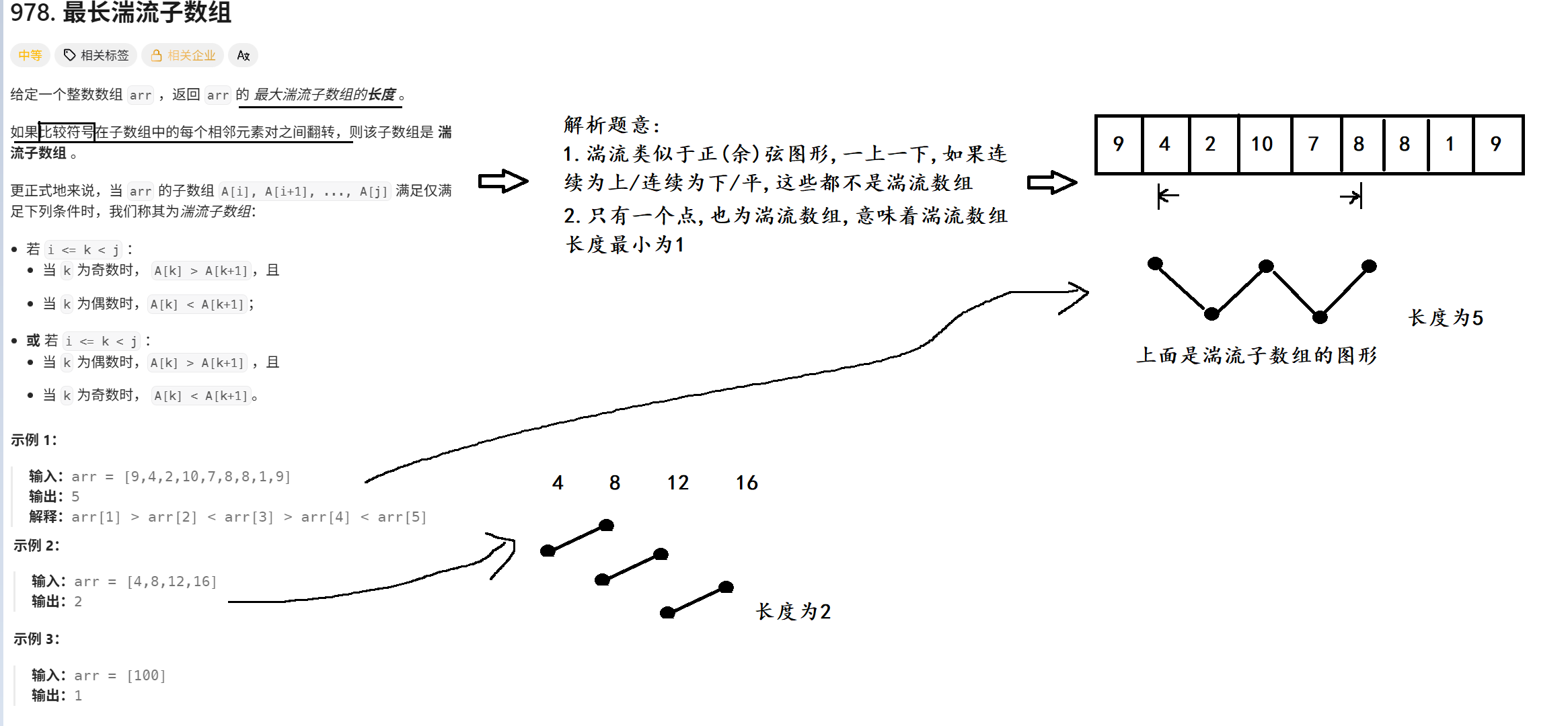
}六. 力扣 978. 最长湍流子数组
1. 题目解析
题目理解很重要, 下面我们把这道题细细解读一下
2. 算法原理
3. 代码
java
public int maxTurbulenceSize(int[] arr) {
int n = arr.length;
int[] f = new int[n];
int[] g = new int[n];
for (int i = 0; i < n; i++) {
f[i] = g[i] = 1;
}
int ret = 1;
for (int i = 1; i < n; i++) {
if (arr[i] > arr[i - 1]) {
f[i] = g[i - 1] + 1;
}else if (arr[i] < arr[i - 1]) {
g[i] = f[i - 1] + 1;
}
ret = Math.max(ret, Math.max(f[i], g[i]));
}
return ret;
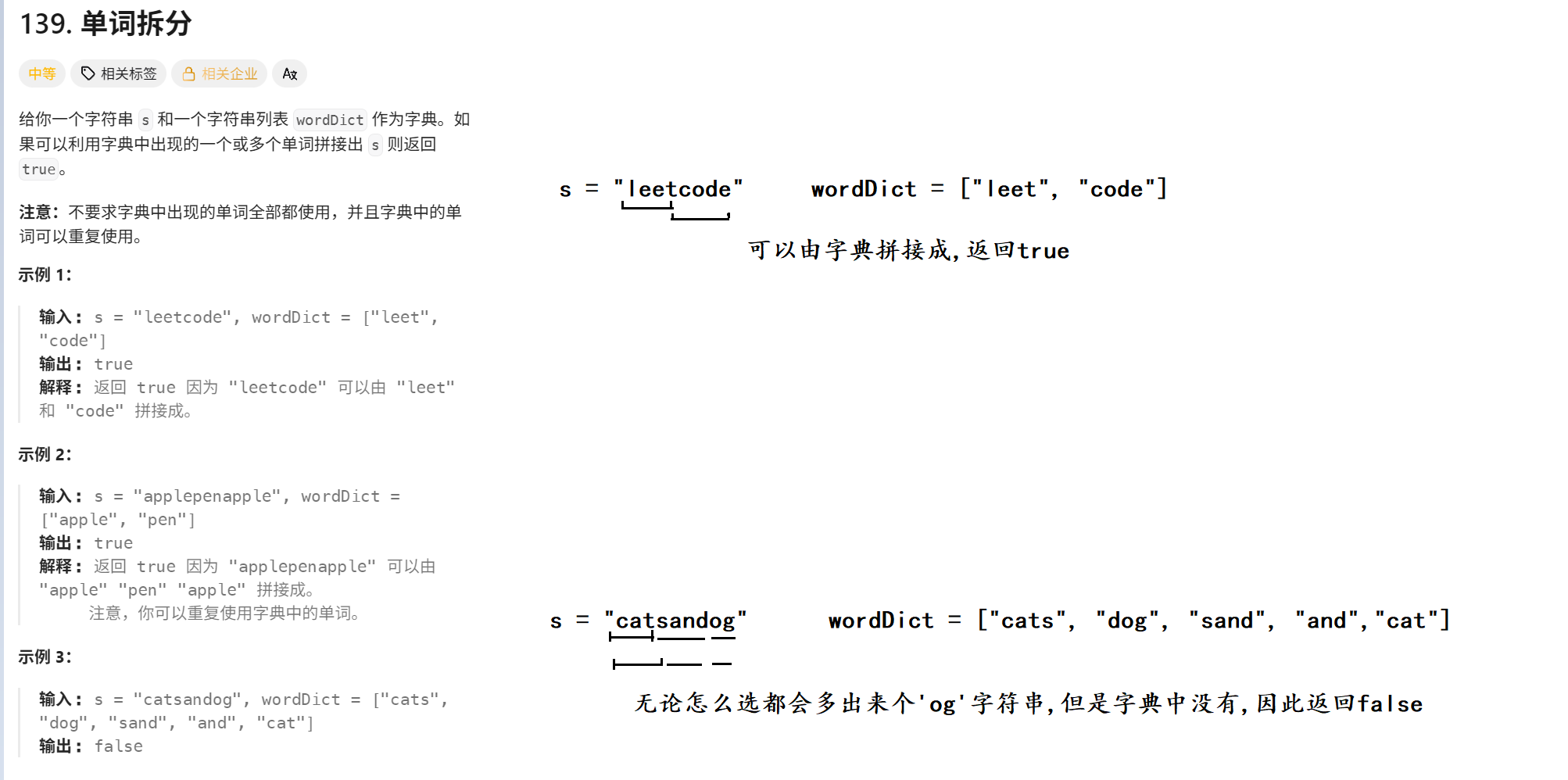
}七. 力扣 139. 单词拆分
1. 题目解析
2. 算法原理
3. 代码
java
public boolean wordBreak(String s, List<String> wordDict) {
int n = s.length();
s = " " + s;
boolean[] dp = new boolean[n + 1];
dp[0] = true;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
String t = new String(s.substring(j, i + 1));
if (dp[j - 1] && wordDict.contains(t)) {
dp[i] = true;
break;
}
}
}
return dp[n];
}八. 力扣 467. 环绕字符串中唯一的子字符串
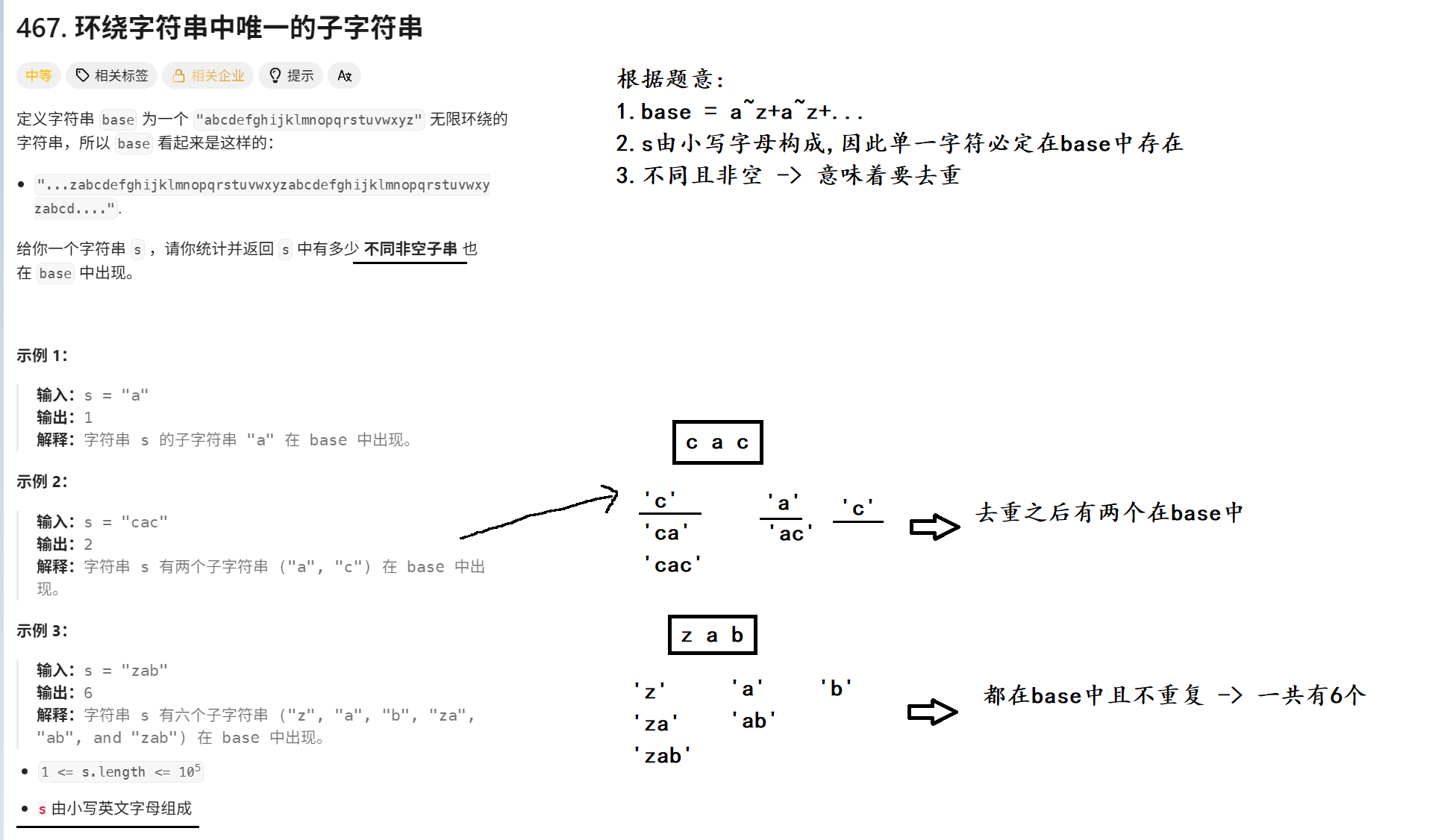
1. 题目解析
2. 算法原理
3. 代码
java
public int findSubstringInWraproundString(String s) {
int n = s.length();
char[] c = s.toCharArray();
int[] dp = new int[n];
dp[0] = 1;
for (int i = 1; i < n; i++) {
if (c[i - 1] + 1 == c[i] || c[i - 1] == 'z' && c[i] == 'a') {
dp[i] = dp[i - 1] + 1;
}else {
dp[i] = 1;
}
}
int[] ch = new int[26];
for (int i = 0; i < n; i++) {
ch[c[i] - 'a'] = Math.max(ch[c[i] - 'a'], dp[i]);
}
int ret = 0;
for (int x : ch) {
ret += x;
}
return ret;
}