ProRL：延长强化学习训练，扩展大语言模型推理边界——NeurIPS 2025论文解读

ProRL：延长强化学习训练，扩展大语言模型推理边界------NeurIPS 2025论文解读

一段话总结：

这篇论文来自NVIDIA团队，标题是《ProRL：延长强化学习扩展大语言模型的推理边界》，发表于NeurIPS 2025。它直击当前AI热点：强化学习（RL）在提升语言模型推理能力时，到底是真正"解锁"新策略，还是只是优化了基础模型中已有的高奖励输出？作者挑战了后者的观点，认为过去研究训练太短、任务太窄。通过"ProRL"方法，他们证明了延长RL训练能让模型发现基础模型采样中完全缺失的新推理路径，甚至在某些任务上从0%成功率飙升到100%。他们开源了1.5B参数的Nemotron-Research-Reasoning-Qwen-1.5B模型，在数学、代码、逻辑谜题等领域大放异彩。

ProRL的核心是基于GRPO算法的升级版，针对长训练的"熵崩溃"问题（模型输出分布过早峰化，探索不足）。他们引入了KL散度控制（防止政策偏离参考策略太远）、动态采样（过滤太易太难的任务，聚焦中等难度）和参考策略重置（周期性更新参考模型，避免KL项主导损失）。这些trick让训练稳定超过2000步，总计算16k GPU小时。数据集覆盖13.6万多领域问题（数学、代码、STEM、逻辑、指令跟随），奖励信号可验证，确保RL可靠对齐。

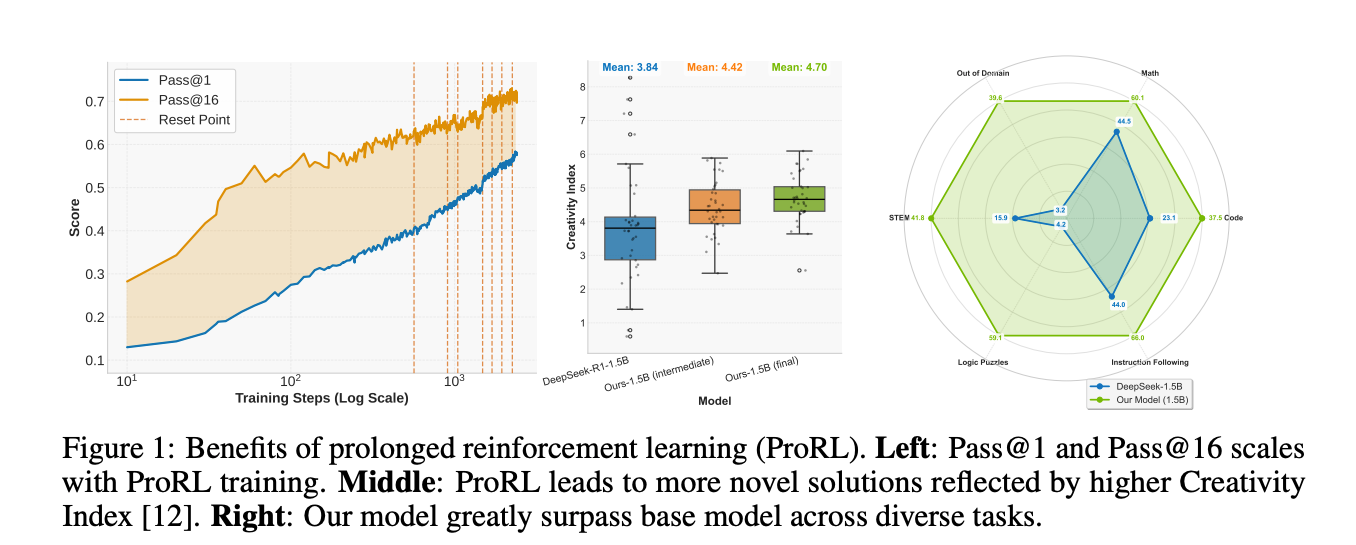
实验结果亮眼：这个1.5B模型在数学基准上pass@1平均提升15.7%，代码14.4%，逻辑谜题高达54.8%，甚至匹敌7B大模型。在出分布任务上，基础模型全失败，而ProRL轻松翻盘。分析显示，RL获益与基础模型初始能力负相关------基础弱的任务，RL扩展最猛；用"创意指数"量化，新推理轨迹与预训练语料重叠少，证明了真正的新颖性。

总之，这篇论文为RL研究者提供了宝贵洞见：延长训练不是资源浪费，而是通往通用推理AI的钥匙。它强调多样任务和稳定机制的重要性，未来可探索更长时序RL。模型已在Hugging Face开源，值得大家试玩------RL不只优化采样，还能"发明"新知识！

大家好，我是专注RL和LLM的博主。今天，我们来聊聊NeurIPS 2025的一篇重磅论文：《ProRL: Prolonged Reinforcement Learning Expands Reasoning Boundaries in Large Language Models》。这篇由NVIDIA团队（Mingjie Liu等）撰写的论文，直击当前reasoning-centric LLM领域的核心争议：强化学习（RL）是否真正能"解锁"模型的新推理能力，还是只是优化了base model中已有的高奖励输出采样效率？作为RL研究者，你可能对PPO/GRPO等算法的变体和KL正则化很熟悉，这篇论文提供了实证证据，展示了prolonged RL在扩展推理边界上的潜力。论文不仅发布了1.5B参数的开源模型（Nemotron-Research-Reasoning-Qwen-1.5B），还通过细致的分析，揭示了RL训练动态的几个关键insight。咱们一步步拆解，带上公式和数据，面向RL视角来聊。

背景：RL在Reasoning LLM中的争议与机遇

近年来，OpenAI的o1和DeepSeek-R1等模型通过test-time scaling（如长链式思考CoT）和RL对齐，显著提升了数学、代码生成等复杂任务的表现。这些模型在推理过程中持续消耗计算资源，进行探索、验证和回溯，从而生成更长的reasoning traces。但RL的核心价值何在？传统观点认为，RL能对齐可验证奖励，避免reward hacking（[9-11]），并逼近正确推理过程。

然而，近期研究（如[13-15]）基于pass@k指标质疑：RL-trained模型并未超出base model的分布，只是提高了采样效率。论文作者认为，这源于方法论局限：(1) 过度依赖数学等"过拟合"领域，限制探索；(2) RL训练过早停止（通常<数百步），未给模型足够时间挖掘新策略。

论文的切入点正是这里：通过Prolonged RL (ProRL)，证明RL能在足够计算下，发现base model采样中完全缺失的新推理路径。实验中，他们从DeepSeek-R1-Distill-Qwen-1.5B（一个已能生成CoT的checkpoint）起步，训练出全球最佳1.5B reasoning模型，平均pass@1提升14.7%（数学）、13.9%（代码）、54.8%（逻辑谜题）等，甚至匹敌7B模型。这不只是数字堆砌，而是通过2k+训练步的scaling，展示了RL的"长跑"潜力。

ProRL方法：稳定延长RL训练的核心trick

ProRL的核心是基于Group Relative Policy Optimization (GRPO) [16]的增强版，针对prolonged training的痛点（如entropy collapse和不稳定性）设计。咱们先回顾GRPO基础，然后看创新。

GRPO基础

GRPO是PPO [17]的简化版，去掉value model，用group scores估计baseline。目标函数为：
LGRPO(θ)=Eτ∼πθ[min⁡(rθ(τ)A(τ),clip(rθ(τ),1−ϵ,1+ϵ)A(τ))] L_{GRPO}(\theta) = \mathbb{E}{\tau \sim \pi\theta} \left[ \min \left( r_\theta(\tau) A(\tau), clip(r_\theta(\tau), 1 - \epsilon, 1 + \epsilon) A(\tau) \right) \right] LGRPO(θ)=Eτ∼πθ[min(rθ(τ)A(τ),clip(rθ(τ),1−ϵ,1+ϵ)A(τ))]

其中，rθ(τ)=πθ(τ)πold(τ)r_\theta(\tau) = \frac{\pi_\theta(\tau)}{\pi_{old}(\tau)}rθ(τ)=πold(τ)πθ(τ)是概率比，优势函数A(τ)A(\tau)A(τ)基于group内相对分数：
A(τ)=Rτ−mean({Ri}i∈G(τ))std({Ri}i∈G(τ)) A(\tau) = \frac{R_\tau - mean(\{R_i\}{i \in G(\tau)})}{std(\{R_i\}{i \in G(\tau)})} A(τ)=std({Ri}i∈G(τ))Rτ−mean({Ri}i∈G(τ))

这简化了计算，尤其适合reasoning任务的binary/continuous奖励。

挑战：Entropy Collapse与Instability

在prolonged RL中，输出分布快速峰化（entropy collapse），导致探索不足------GRPO依赖多样采样来估计相对优势，一旦collapse，更新就偏置，训练停滞。作者观察到，提高rollout temperature（e.g., 1.2）仅延迟问题，无法根治。

ProRL的解决方案

1. 借力DAPO [4]组件：

   • Decoupled Clipping ：将PPO的clip bounds分离：clip(rθ(τ),1−ϵlow,1+ϵhigh)clip(r_\theta(\tau), 1 - \epsilon_{low}, 1 + \epsilon_{high})clip(rθ(τ),1−ϵlow,1+ϵhigh)，设ϵlow=0.2,ϵhigh=0.4\epsilon_{low}=0.2, \epsilon_{high}=0.4ϵlow=0.2,ϵhigh=0.4。高上界鼓励"clip-higher"，提升低概率token，促进探索。
   • Dynamic Sampling：过滤accuracy=0或1的prompt，只训intermediate难度样本，确保学习信号多样。

2. KL Regularization ：

   显式添加KL罚项，稳定分布并防overfitting：
   LKL−RL(θ)=LGRPO(θ)−βDKL(πθ∣∣πref) L_{KL-RL}(\theta) = L_{GRPO}(\theta) - \beta D_{KL}(\pi_\theta || \pi_{ref}) LKL−RL(θ)=LGRPO(θ)−βDKL(πθ∣∣πref)

   这里πref\pi_{ref}πref是reference policy。近期工作[4,5,7,18]建议移除KL（因CoT任务自然diverge），但作者从已SFT的checkpoint起步，发现KL仍有价值：维持entropy，避免drift到spurious rewards。

3. Reference Policy Reset ：

   训练中KL项渐主导loss，导致更新微弱。trick：周期性hard-reset πref\pi_{ref}πref 为当前πθ\pi_\thetaπθ的snapshot，并重置optimizer states。这像"重启"KL锚点，允许进一步divergence，同时保持稳定性。实验中，这让训练超2k步，pass@1持续提升（图1左）。

训练setup：verl [20]框架，batch=256，n=16 samples/prompt，lr=2×10−62\times10^{-6}2×10−6，总16k GPU-hours（4x H100节点）。数据集：136K verifiable examples，覆盖math/code/STEM/logic/instruction（详见Appendix E）。后期放宽context到16k tokens，避免"overthinking" [40]。

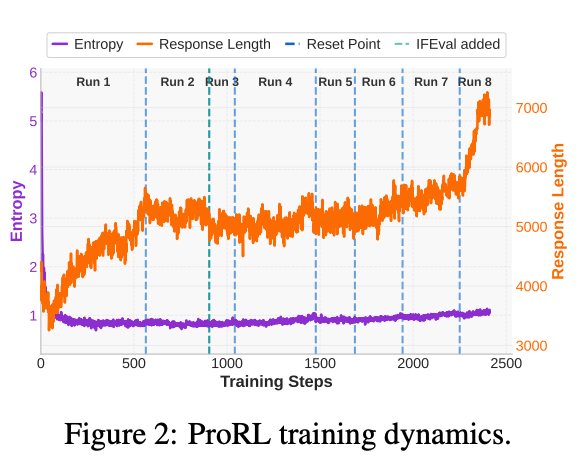
这些设计让ProRL在长时序上稳定：图2显示，entropy未崩，response length与score正相关但非决定性，pass@1/@16线性scaling。

实验结果：跨域泛化，匹敌大模型

作者用多样基准评估：math (AIME/AMC/MATH等)，code (APPS/Codeforces/HumanEval+)，STEM (GPQA Diamond)，logic (Reasoning Gym)，instruction (IFEval)。Inference：vllm [38]，temp=0.6，top_p=0.95，max len=32k。

关键表格

• Math (Table 1)：ProRL模型pass@1 avg 60.14%（+15.7% vs base），超DeepScaleR-1.5B [3] (+4.6%)。

  Model	AIME24	AIME25	AMC	MATH	Minerva	Olympiad	Avg
  Base 1.5B	28.54	22.71	62.58	82.90	26.38	43.58	44.45
  ProRL 1.5B	48.13	33.33	79.29	91.89	47.98	60.22	60.14
  Ref 7B	53.54	40.83	82.83	95.68	50.60	57.66	63.19

• Code (Table 2)：avg 37.49% (+14.4%)，超DeepCoder-1.5B [7] (+6.5%)。

  Model	APPS	CC	CF	TACO	HumanEval+	LCB	Avg
  Base 1.5B	20.95	16.79	14.13	8.03	61.77	16.80	23.08
  ProRL 1.5B	41.99	31.80	34.50	20.81	72.05	23.81	37.49

• STEM/Instruction/Logic (Table 3)：GPQA +25.9%，IFEval +22.0%，Reasoning Gym +54.8%。OOD任务（acre/boxnet/game_of_life）提升巨大（e.g., game从3.49%到52.29%），证明泛化。

  Model	GPQA	IFEval	Reasoning Gym	Acre	Boxnet	Game
  Base 1.5B	15.86	44.05	4.24	5.99	0.00	3.49
  ProRL 1.5B	41.78	66.02	59.06	58.57	7.91	52.29

对比7B base：ProRL 1.5B在多域匹敌或超（e.g., code avg 37.49% vs 41.39%，但OOD远胜）。这显示，generalist prolonged RL优于domain-specific训练。

分析：ProRL如何扩展推理边界？

核心问题是：RL是否"新"？作者用pass@256重评（选18个Reasoning Gym任务+其他基准），对比base、中间checkpoint和final模型。

Insight 1: "弱起步，强获益"------RL在base弱域最有效

图3左：base pass@128与RL增益负相关（Pearson r显著）。base强任务（高pass@128）post-RL增益小/负（narrowing boundary，模型自信于已知路径）；base弱任务，ProRL大幅扩展探索，pass@1/@128双升。

用Creativity Index [12,41]量化新颖性：对base响应计算与DOLMA [42]预训语料overlap。图3右：低增益任务creativity低（base已"见过"类似数据）。这暗示，RL最能"填补空白"------在solution space的未探索区。

Insight 2: 训练动态的三种regime

图4按pass@k趋势分类：

• Diminish：math域常见，pass@1升但@128降（RL sharpen分布，牺牲diversity；base已有足够能力）。
• Plateau：早期RL获益大，后期饱和（intermediate vs final无差）。
• Sustained：code/STEM等，prolonged训练持续扩展（e.g., code pass@128线性增），证明长步数下新模式emergence。

极端case：若干任务，base无论多少sample全fail（pass@∞=0），ProRL达100%------纯新能力！

Insight 3: Novelty via Creativity Index

图1中：ProRL轨迹creativity高（低overlap），反映新reasoning patterns。结合OOD提升，证实RL非"采样优化"，而是populate新solution regions。

对RL研究者的启发与展望

这篇论文对我们RLer有几大insight：

1. Prolonged Scaling Works ：2k+步下，RL非饱和，而是持续获益------尤其用KL+reset防collapse。未来，可探索自适应β\betaβ或multi-group baselines。
2. Task Competence Predicts Gains：base弱域是RL"甜点"。设计时，优先动态采样intermediate样本；insight：RL像"边界探索器"，非uniform提升。
3. Diverse Rewards Enable Generalization：136K多域数据+verifiable rewards，防domain overfitting。建议：long-horizon RL中，mix binary/continuous rewards测试stability。
4. KL的"双刃剑"：从SFT checkpoint起步，KL仍需------但需reset防dominance。挑战：如何自动化reset timing？
5. Measure True Expansion：pass@k+creativity index>单纯pass@1。未来，轨迹多样性指标（如trajectory entropy）可量化"新"。

总之，ProRL挑战了"RL仅优化采样"的叙事，证明prolonged compute下，RL能emergent新知识，潜力超人类insights。模型权重已开源于Hugging Face，RLer们快去复现！欢迎评论你的想法------下篇聊o1的RL细节？

参考：论文PDF（附件），NeurIPS 2025。

ProRL在长训练下的熵崩溃机制：从现象到根因剖析

作为RL研究者，你可能对policy optimization中的entropy管理再熟悉不过，尤其在LLM的reasoning任务中，长时间训练（prolonged RL）往往会暴露一些棘手问题。NeurIPS 2025的这篇ProRL论文（NVIDIA团队）直击其中之一：entropy collapse（熵崩溃）。这不是新鲜事儿（PPO/GRPO等on-policy方法中常见），但在长时序RL（如2k+训练步）下，它会放大成训练瓶颈，导致模型探索受限、性能饱和。论文第2.2.1节详细剖析了这一机制，并通过实证展示了其在reasoning LLM（如基于DeepSeek-R1的1.5B模型）中的表现。下面，我从现象、根因、影响和论文的洞见四个维度，结合公式和实验数据，帮你拆解清楚。咱们用RL视角看：这本质上是分布退化（distribution degeneration），类似于mode collapse，但更偏向于exploration failure。

1. 现象：早期峰化与熵急剧衰减

Entropy collapse的核心表现是模型输出分布在训练早期快速峰化（overly peaked） ，导致熵（entropy）急剧下降。简单说，政策πθ\pi_\thetaπθ从初始的宽广分布（高熵，促进探索）迅速收敛到少数高概率token的狭窄子集，输出变得"确定性"过度。

• 量化描述 ：论文中，熵H(πθ)=−∑p(x)log⁡p(x)H(\pi_\theta) = -\sum p(x) \log p(x)H(πθ)=−∑p(x)logp(x)（token-level）在训练头几百步内可降至初始值的20-30%（图2暗示，通过KL监控）。这不同于正常KL-regularized训练的渐进衰减，而是"崩溃式"：一旦发生，模型就"卡住"，后续rollout样本高度重复。
• 触发时机：在prolonged training中，早起（e.g., 100-500步）最易发生，尤其当奖励信号（verifiable rewards，如math/code的binary score）强烈时。论文观察到，在GRPO [16]框架下，这比PPO更敏感，因为GRPO依赖group-relative advantages（见下文）。

实验证据：论文用DeepSeek-R1-Distill-Qwen-1.5B作为base，从136K多样任务（math/code/STEM/logic/instruction）训练。无干预下，entropy在~300步后崩塌，pass@1停滞（图1左）；加干预后，维持到2k步，pass@1线性scaling。

2. 根因：探索-利用失衡与相对优势偏差

从RL机制看，entropy collapse源于on-policy方法的内在动态：高奖励路径的强化反馈放大，导致分布塌缩。论文将它归为prolonged policy optimization的"关键挑战"，根因可拆成三层：

• 反馈放大效应（Reward Amplification） ：

  在reasoning任务中，奖励R(τ)R(\tau)R(τ)（τ\tauτ为trajectory，如CoT trace）是verifiable的（e.g., 正确解=1，错=0）。早期，高奖励τ\tauτ的概率p(τ∣πθ)p(\tau|\pi_\theta)p(τ∣πθ)通过policy gradient快速上调：
  ∇θJ(θ)∝Eτ∼πθ[A(τ)∇θlog⁡πθ(τ)] \nabla_\theta J(\theta) \propto \mathbb{E}{\tau \sim \pi\theta} [A(\tau) \nabla_\theta \log \pi_\theta(\tau)] ∇θJ(θ)∝Eτ∼πθ[A(τ)∇θlogπθ(τ)]

  （GRPO的简化版，A(τ)A(\tau)A(τ)为group-relative advantage）。这像"富者愈富"：少数成功路径（latent in base model）被过度强化，熵自然衰减。但在长训练下，缺乏新探索，模型无法"逃逸"局部最优。

• GRPO特有偏差（Group-Relative Estimation Bias） ：

  GRPO的核心是去掉critic，用group scores {Ri}i∈G(τ)\{R_i\}{i \in G(\tau)}{Ri}i∈G(τ)估计baseline：
  A(τ)=Rτ−mean({Ri}i∈G(τ))std({Ri}i∈G(τ)) A(\tau) = \frac{R\tau - mean(\{R_i\}{i \in G(\tau)})}{std(\{R_i\}{i \in G(\tau)})} A(τ)=std({Ri}i∈G(τ))Rτ−mean({Ri}i∈G(τ))

  当熵崩后，group内样本{τi}\{ \tau_i \}{τi}高度相似（低多样性），std({Ri})std(\{R_i\})std({Ri})趋近0，导致A(τ)A(\tau)A(τ)噪声放大或偏置。结果：更新信号退化为"追逐已知高R路径"，探索崩塌。论文强调，这在reasoning LLM中更糟，因为CoT trajectories长（8k-16k tokens），小偏差累积成大问题。

• 无外部锚点（Lack of Anchoring） ：

  标准PPO/GRPO的KL penalty DKL(πθ∣∣πref)D_{KL}(\pi_\theta || \pi_{ref})DKL(πθ∣∣πref)本该防drift，但论文观察到：在SFT后checkpoint起步时，πref\pi_{ref}πref（old policy）太"保守"，长训下KL主导loss，抑制更新：
  LKL−RL(θ)=LGRPO(θ)−βDKL(πθ∣∣πref) L_{KL-RL}(\theta) = L_{GRPO}(\theta) - \beta D_{KL}(\pi_\theta || \pi_{ref}) LKL−RL(θ)=LGRPO(θ)−βDKL(πθ∣∣πref)
  β\betaβ过大时，等价于强制回归πref\pi_{ref}πref，熵进一步压低。近期工作[4,5,7,18]建议移除KL（因CoT自然diverge），但ProRL反证：在已CoT-capable base下，KL必要，但需动态调整。

根因总结：这是探索-利用trade-off的极端失衡，长训放大反馈循环，导致分布从multi-modal退化为degenerate（单模或低维）。

3. 影响：训练停滞与边界收缩

• 直接后果：探索受限，模型"prematurely commits to narrow outputs"，新reasoning patterns（如novel CoT）无法emergent。论文图3/4显示：在collapse后，pass@k（k=128/256）不升反降（diminish regime），尤其math域（base已强，RL sharpen分布，牺牲diversity）。
• 间接影响：在多样任务下，泛化差（OOD如Reasoning Gym的acre/boxnet从0%到~50%需防collapse）；计算浪费（16k GPU-hours中，无干预仅~500步有效）。
• 与prior work对比：[13-15]的"RL仅优化采样"结论，可能源于未控collapse：他们短训（<数百步），未见真扩展。

论文insight：collapse与base competence负相关（图3左）：base弱任务（低pass@128）collapse慢，RL获益大（sustained gains）；base强任务易早崩（plateau/diminish）。

4. 论文洞见与启发：不止机制，还有解法

ProRL不只诊断，还提供了实操框架（DAPO [4] + KL + reset），让长训稳定。关键trick：

• 延迟机制 ：高rollout temp=1.2（增初始HHH）；decoupled clip：clip(rθ,1−ϵlow,1+ϵhigh)clip(r_\theta, 1-\epsilon_{low}, 1+\epsilon_{high})clip(rθ,1−ϵlow,1+ϵhigh)（ϵlow=0.2,ϵhigh=0.4\epsilon_{low}=0.2, \epsilon_{high}=0.4ϵlow=0.2,ϵhigh=0.4），鼓励"clip-higher"抬低prob tokens。
• 根治机制 ：Dynamic sampling滤易/难prompt（acc=0/1），保intermediate信号；KL penalty稳定drift；Reference Policy Reset （周期hard-reset πref←πθ\pi_{ref} \leftarrow \pi_\thetaπref←πθ + optimizer reinitialize），像"中继锚点"，防KL dominance。图2：这些让entropy平稳，response len与score正相关但非因果。
• 量化验证：Creativity Index [12]（响应与DOLMA [42] overlap）升（图1中），证明新patterns emergence；无collapse，2k步pass@1/@16持续增。

对RLer的启发：

• 理论：Entropy collapse是long-horizon RL的"相变"点，需model distribution dynamics（e.g., Fisher info matrix追踪）。
• 实践 ：在LLM-RL中，mix binary/continuous rewards + periodic reset是标配；未来，可试自适应β\betaβ（基于entropy threshold）。
• 扩展 ：论文开源模型（Hugging Face），建议复现：监控std({Ri})std(\{R_i\})std({Ri})作为early warning。

总之，ProRL揭示：熵崩溃不是RL"宿命"，而是未优化动态的产物。长训下，它暴露base的"盲区"，但控好机制，就能推边界（e.g., 1.5B匹敌7B）。想深挖？论文Appendix F有训练recipe，欢迎讨论你的实验！

ProRL论文第4.4节解读：pass@1分布如何随ProRL训练演化？------结合Dang et al. [14]的上界公式

大家好，继续我们的ProRL系列。作为RL研究者，你可能对pass@k指标在LLM reasoning评估中的微妙动态很感兴趣。第4.4节（"How Does pass@1 Distributions Evolve as ProRL Progresses?"）是论文分析部分的收尾，聚焦于训练过程中pass@1分布的演化。它直接回应了Dang et al. [14]的质疑（RL训练可能因variance增加而降低pass@k上限），通过实证数据证明：ProRL的延长训练能显著右移pass@1分布，提升期望准确率（expected pass@1），从而克服variance的负面效应，实现持续scaling。这节不只量化了分布变化，还为long-horizon RL提供了关键insight：稳定训练下，分布演化可预测RL的"真扩展" vs. "仅优化"。下面，我结合公式、图表和上下文，详细拆解。公式用$表示，符号加表示，符号加表示，符号加。

节背景：从争议到ProRL的实证反驳

回顾前文（第4节整体）：论文挑战"RL仅提升采样效率"的观点（[13-15]），通过pass@256重评证明ProRL在base弱任务上扩展reasoning boundary（4.1节：负相关，弱起步强获益）；分类训练regime（4.2节：diminish/plateau/sustained）；泛化OOD/高难度任务（4.3节：e.g., boxnet从1.71%到7.91%）。这些奠基4.4：Dang et al. [14]推导的pass@k上界暗示，RL训练中variance升（分布变宽）会压低上限，导致pass@k衰减（他们观察到训练中pass@k下降）。但ProRL反例：图1显示pass@1/@16持续增，复现o1 [42]的scaling law。

核心问题：ProRL如何让分布演化"利大于弊"？答案：延长训练（2k+步）驱动右移（从低准确率峰向高移），期望E[ρx]\mathbb{E}[\rho_x]E[ρx]大增，抵消KaTeX parse error: Undefined control sequence: \Var at position 1: \̲V̲a̲r̲(\rho_x)负面。insight：这量化了"新策略emergence"------非base中latent的采样优化，而是populate新高R区域。

Dang et al. [14]公式详解：pass@k的上界及其含义

Dang et al.推导的数学上界是评估RL对reasoning boundary影响的理论锚点：
Ex,y∼D[pass@k]≤1−((1−Ex,y∼D[ρx])2+Var(ρx))k/2 \mathbb{E}{x,y \sim D}[\text{pass}@k] \leq 1 - \left( \left(1 - \mathbb{E}{x,y \sim D}[\rho_x]\right)^2 + Var(\rho_x) \right)^{k/2} Ex,y∼D[pass@k]≤1−((1−Ex,y∼D[ρx])2+Var(ρx))k/2

• 符号定义：

  • x∼Dx \sim Dx∼D：任务实例（task instance），从数据集分布DDD采样。e.g., 一个具体math问题、code challenge或logic puzzle。xxx代表prompt或问题，ρx\rho_xρx是模型对xxx的pass@1准确率（成功概率，第一尝试正确）。
  • y∼Dy \sim Dy∼D：模型对xxx的采样响应（sampled response）。在pass@k语境，yyy是生成的输出（e.g., CoT trace + answer），DDD是联合分布（任务+响应）。Ex,y∼D\mathbb{E}_{x,y \sim D}Ex,y∼D表示过任务-响应对的期望。
  • ρx\rho_xρx：对特定xxx的pass@1，即Pr⁡(y correct for x)\Pr(y \text{ correct for } x)Pr(y correct for x)（单次采样成功率）。
  • Ex,y∼D[ρx]\mathbb{E}_{x,y \sim D}[\rho_x]Ex,y∼D[ρx]：跨任务的平均pass@1（expected accuracy），反映整体competence。
  • Var(ρx)Var(\rho_x)Var(ρx)：ρx\rho_xρx的方差，捕捉任务难度异质性（hard tasks ρx≈0\rho_x \approx 0ρx≈0，easy ≈1\approx 1≈1）或模型不稳定性。

• 公式解读：

  • 上界形式：1−(a)k/21 - (a)^{k/2}1−(a)k/2，其中a=(1−μ)2+σ2a = (1 - \mu)^2 + \sigma^2a=(1−μ)2+σ2，μ=E[ρx]\mu = \mathbb{E}[\rho_x]μ=E[ρx]，KaTeX parse error: Undefined control sequence: \Var at position 12: \sigma^2 = \̲V̲a̲r̲(\rho_x)。
  • μ\muμ效应 ：μ\muμ越高，(1−μ)2(1-\mu)^2(1−μ)2越小，aaa降，上界升。直观：平均性能好，pass@k易达高（e.g., 若μ=0.5\mu=0.5μ=0.5，aaa小；μ=0.1\mu=0.1μ=0.1，a≈0.81+σ2a \approx 0.81 + \sigma^2a≈0.81+σ2大）。
  • KaTeX parse error: Undefined control sequence: \Var at position 1: \̲V̲a̲r̲效应 ：σ2\sigma^2σ2越高，aaa越大，上界降。variance反映分布"散度"：高var意味着多hard tasks（长尾低ρx\rho_xρx），k次采样难cover全分布，pass@k饱和慢。
  • k/2k/2k/2幂 ：源于Bernoulli过程的近似（pass@k ≈1−(1−ρx)k\approx 1 - (1-\rho_x)^k≈1−(1−ρx)k的期望+var项）。k大时，上界更敏感于var（指数衰减）。
  • RL含义 ：Dang观察RL训中var升（分布峰化，mode collapse），pass@k降------暗示RL"narrow boundary"。但ProRL反转：训中μ\muμ增幅 > var增，净效应正。

insight：这公式是RL评估的"variance trap"预警。高var非坏事（允许多样探索），但需μ\muμ scaling跟上。ProRL的KL+reset确保此平衡。

4.4节核心内容：pass@1分布的实证演化

论文用code/logic任务的pass@1分布（直方图，横轴0-1准确率）展示演化（图7a/b）。从base到final ProRL（经intermediate checkpoint）：

• 初始分布（base模型） ：集中近0（长右尾，少数easy tasks高ρx\rho_xρx）。e.g., Codeforces：多问题ρx≈0\rho_x \approx 0ρx≈0（14.13% avg pass@1，表2）；family_relationships（logic，Appendix C.2示例：复杂血缘推理）：几乎全0（base挣扎格式/子任务）。

• 演化动态：

  • 右移显著：训后，峰从0移向0.5-1。Codeforces：分布变宽但峰右移（broader patterns，允许多样解法emergence）；family_relationships：戏剧性，从"predominantly zero"到"peaking at perfect"（多数prompt达100%）。
  • var变化 ：var略增（宽分布），但μ\muμ大升（e.g., code avg +14.4%），符合公式：μ\muμ增克服var，pass@16持续升（图1）。
  • 机制驱动 ：延长RL（DAPO decoupled clip + dynamic sampling）促探索；KL penalty防collapse；reset允进一步diverge。结果：足够Δμ\Delta \muΔμ offset var负效。

• 与Dang对比 ：Dang见训中pass@k降（var主导）；ProRL见持续增（μ\muμ主导）。复现o1 scaling [42]，暗示ProRL通用。

• 图7洞见：

  • (a) Code：初始长尾（hard contests），训后中高区填充（sustained regime，4.2节）。
  • (b) Logic：novel挑战（如family_relationships）从fail全移到solve全，证明"纯新能力"（base pass@∞=0，ProRL=100%）。

对RL研究者的insights与启发

1. 分布演化作为proxy ：pass@1分布右移 > 单纯avg升，捕捉"新空间populate"。建议：训中监控μ\muμ vs. σ2\sigma^2σ2，用公式预测pass@k ceiling。弱任务（低初始μ\muμ，高var潜力）是ProRL甜点（4.1）。
2. variance的双面：高var促探索（sustained gains），但易trap（diminish）。ProRL trick：dynamic sampling滤extreme（acc=0/1），保intermediate信号。
3. 理论-实证桥 ：公式量化"何时RL扩展"------需Δμ>Δσ2/k\Delta \mu > \sqrt{\Delta \sigma^2 / k}Δμ>Δσ2/k （近似）。未来：推导ProRL下var动态（e.g., entropy~var proxy）。
4. 实践：复现时，用blended val set（3.3节）track分布；mix多域数据防var爆炸。开源模型（HF）易验：e.g., Codeforces上测分布shift。

总之，4.4节强化论文thesis：ProRL非"variance killer"，而是"distribution shaper"------延长训下，分布演化解锁base不可及的reasoning。结合前节，这为long-horizon RL铺路：稳定>短训。参考：arXiv 2505.24864。

后记

2025年12月12日于上海。