一、算法分类概述
排序算法是计算机科学中最基础且重要的算法类别,用于将数据元素按照特定顺序重新排列。根据是否通过比较元素大小进行排序,可分为比较排序 和非比较排序两大类。以下是11种常见排序算法的全面对比分析。
二、基本比较排序算法
1. 冒泡排序(Bubble Sort)
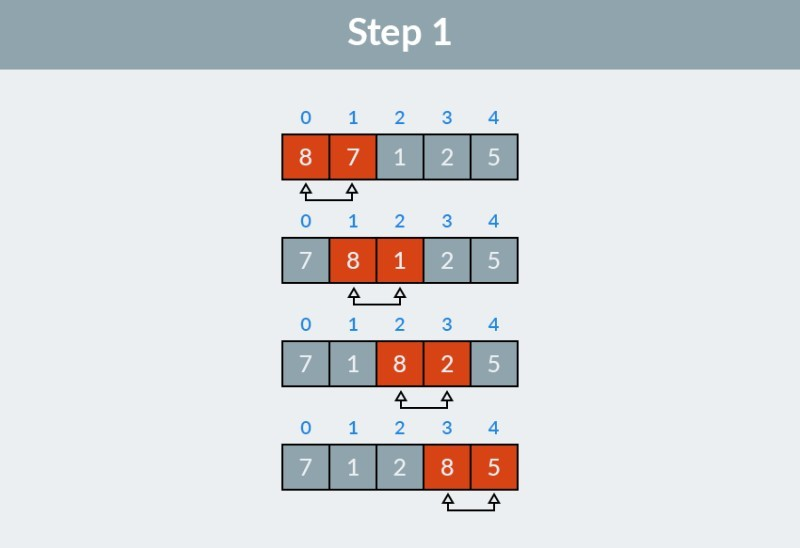
算法原理:通过重复遍历数组,依次比较相邻元素,若顺序错误则交换位置,使较大元素逐步"浮"到数组末端。每轮遍历会确定一个元素的最终位置。
核心步骤:
-
从数组第一个元素开始,比较相邻元素
-
如果前一个元素大于后一个元素,交换它们的位置
-
重复上述过程,直到整个数组有序
复杂度分析:
-
时间复杂度:最好情况O(n)(已排序时),平均和最坏情况O(n²)
-
空间复杂度:O(1)(原地排序)
-
稳定性:稳定排序算法
适用场景:适用于小规模数据排序、教学演示、数据基本有序的场景。当数据规模超过1000时,建议使用更高效的算法。
2. 选择排序(Selection Sort)

算法原理:每次从未排序部分选择最小(或最大)元素,放到已排序部分的末尾。每轮遍历只进行一次交换操作。
核心步骤:
-
在未排序序列中找到最小元素
-
将其与未排序序列的第一个元素交换
-
重复上述过程,直到所有元素排序完成
复杂度分析:
-
时间复杂度:O(n²)(无论数据是否有序)
-
空间复杂度:O(1)(原地排序)
-
稳定性:不稳定排序算法
适用场景:适用于小规模数据、内存受限环境、交换操作成本较高的场景。每轮只交换一次,在交换成本高时优势明显。
3. 插入排序(Insertion Sort)
算法原理:将数组分为已排序和未排序两部分,每次从未排序部分取出第一个元素,在已排序部分从后向前扫描,找到合适位置插入,使已排序部分保持有序。
核心步骤:
-
将第一个元素视为已排序
-
取出下一个元素,在已排序序列中从后向前扫描
-
找到合适位置后插入
-
重复上述过程,直到所有元素排序完成
复杂度分析:
-
时间复杂度:最好情况O(n)(已排序时),平均和最坏情况O(n²)
-
空间复杂度:O(1)(原地排序)
-
稳定性:稳定排序算法
适用场景:适用于小规模数据、近乎有序的数据、作为高级算法的组成部分(如Timsort中的插入排序优化)。
三、高效分治排序算法
4. 快速排序(Quick Sort)
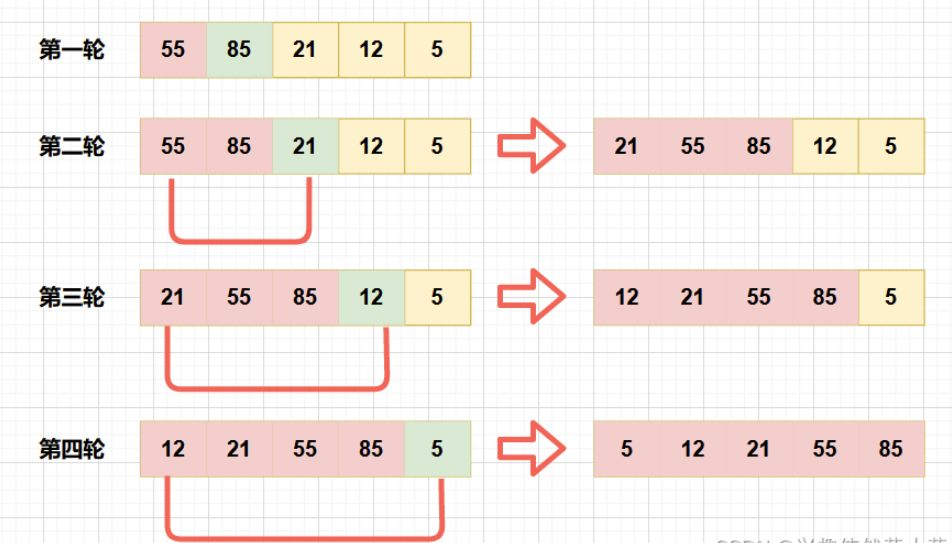
算法原理:采用分治策略,选择一个基准元素,将数组分为小于基准和大于基准的两部分,然后递归地对这两部分进行快速排序。
核心步骤:
-
从数组中选择一个基准元素(pivot)
-
将数组分为两部分:小于基准的放在左边,大于基准的放在右边
-
递归地对左右两部分进行快速排序
复杂度分析:
-
时间复杂度:平均情况O(n log n),最坏情况O(n²)(如已排序且基准选择不当)
-
空间复杂度:O(log n)(递归栈空间)
-
稳定性:不稳定排序算法
适用场景:适用于大规模数据排序,是实际应用中最常用的排序算法之一。通过优化基准选择策略(如三数取中法、随机选择),可以避免最坏情况。
5. 归并排序(Merge Sort)
算法原理:采用分治思想,将数组递归地拆分为两半,直到每个子数组只有一个元素,然后将有序子数组合并成一个更大的有序数组。
核心步骤:
-
将数组递归地拆分为两半,直到每个子数组只有一个元素
-
将两个有序子数组合并成一个有序数组
-
重复合并过程,直到整个数组有序
复杂度分析:
-
时间复杂度:O(n log n)(无论数据是否有序)
-
空间复杂度:O(n)(需要额外存储空间)
-
稳定性:稳定排序算法
适用场景:适用于大规模数据排序、外部排序(处理存储在磁盘上的大数据集)、需要稳定排序的场景。虽然空间复杂度较高,但其稳定的O(n log n)性能使其在处理大规模数据时具有显著优势。
6. 堆排序(Heap Sort)
算法原理:利用堆这种数据结构,将数组构造成一个大顶堆(或小顶堆),然后将堆顶元素与末尾元素交换,重新调整堆,重复此过程直到整个数组有序。
核心步骤:
-
将待排序序列构造成一个大顶堆
-
将堆顶元素与末尾元素交换,此时末尾元素为最大值
-
重新调整堆,使其满足堆性质
-
重复上述过程,直到整个序列有序
复杂度分析:
-
时间复杂度:O(n log n)(所有情况)
-
空间复杂度:O(1)(原地排序)
-
稳定性:不稳定排序算法
适用场景:适用于数据量非常大的场合(百万数据级别),不需要大量递归或多维暂存数组,适合内存受限环境。
四、改进型排序算法
7. 希尔排序(Shell Sort)
算法原理:是插入排序的改进版本,通过将数组按增量分组,对每组进行插入排序,然后逐步缩小增量,最终对整个数组进行一次插入排序。
核心步骤:
-
选择一个增量序列(如n/2, n/4, ..., 1)
-
按增量将数组分组,对每组进行插入排序
-
逐步缩小增量,重复分组排序
-
当增量为1时,对整个数组进行插入排序
复杂度分析:
-
时间复杂度:平均O(n log n)到O(n²),取决于增量序列的选择
-
空间复杂度:O(1)(原地排序)
-
稳定性:不稳定排序算法
适用场景:适用于中等规模数据(5000以下),比冒泡排序快5倍,比插入排序快2倍,但比快速排序、归并排序、堆排序慢。
8. 鸡尾酒排序(Cocktail Sort)
算法原理:冒泡排序的改进版本,也称为双向冒泡排序,通过双向遍历数组来提升性能。
核心步骤:
-
从左到右遍历,将最大元素移到末尾
-
从右到左遍历,将最小元素移到开头
-
缩小排序范围,重复双向遍历
-
当没有交换发生时结束
复杂度分析:
-
时间复杂度:最好情况O(n),平均和最坏情况O(n²)
-
空间复杂度:O(1)(原地排序)
-
稳定性:稳定排序算法
适用场景:适用于部分有序的小规模数据,比传统冒泡排序效率略高,但实际应用较少。
五、非比较排序算法
9. 计数排序(Counting Sort)
算法原理:非比较排序算法,通过统计每个元素出现的次数,然后根据统计结果确定每个元素在有序序列中的位置。
核心步骤:
-
找出待排序数组中的最大值和最小值
-
统计每个元素出现的次数
-
根据统计结果,计算每个元素的最终位置
-
将元素放入正确位置
复杂度分析:
-
时间复杂度:O(n + k),其中k为数据范围
-
空间复杂度:O(n + k)
-
稳定性:稳定排序算法
适用场景:适用于数据范围较小且为整数的场景,当数据范围k远大于数据量n时,空间消耗较大。
10. 桶排序(Bucket Sort)
算法原理:将数据分到有限数量的桶中,每个桶再分别排序,最后合并所有桶的结果。
核心步骤:
-
设置一个定量的数组当作空桶
-
遍历输入数据,将数据分配到对应的桶中
-
对每个非空桶进行排序
-
从非空桶中把排好序的数据拼接起来
复杂度分析:
-
时间复杂度:平均O(n + k),最坏O(n²)(所有元素在一个桶中)
-
空间复杂度:O(n + k)
-
稳定性:稳定排序算法(取决于桶内排序算法的稳定性)
适用场景:适用于数据分布均匀且数据范围有限的情况,特别适合浮点数排序。
11. 基数排序(Radix Sort)
算法原理:按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。
核心步骤:
-
取得数组中的最大数,并取得位数
-
从最低位开始,依次对每一位进行排序(通常使用计数排序或桶排序)
-
重复上述过程,直到最高位
复杂度分析:
-
时间复杂度:O(d × (n + k)),其中d为位数,k为基数
-
空间复杂度:O(n + k)
-
稳定性:稳定排序算法
适用场景:适用于整数或字符串等位数数据排序,当位数d较小且数据量n较大时,性能优异。
六、11种排序算法综合对比表
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 空间复杂度 | 稳定性 | 适用场景 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 | 小规模数据、教学演示 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 | 小规模数据、交换成本高 |
| 插入排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 | 小规模数据、近乎有序 |
| 快速排序 | O(n log n) | O(n²) | O(n log n) | O(log n) | 不稳定 | 大规模数据、实际应用 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 | 大规模数据、稳定需求 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 不稳定 | 大规模数据、内存受限 |
| 希尔排序 | O(n log n) | O(n²) | O(n) | O(1) | 不稳定 | 中等规模数据 |
| 鸡尾酒排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 | 部分有序小规模数据 |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(n + k) | 稳定 | 数据范围小的整数 |
| 桶排序 | O(n + k) | O(n²) | O(n) | O(n + k) | 稳定 | 数据分布均匀 |
| 基数排序 | O(d × (n + k)) | O(d × (n + k)) | O(d × (n + k)) | O(n + k) | 稳定 | 整数或字符串排序 |
七、算法选择建议
-
小规模数据(n < 50):优先选择插入排序或冒泡排序
-
中等规模数据(50 < n < 1000):快速排序通常表现最佳
-
大规模数据(n > 1000):快速排序或归并排序
-
需要稳定排序:选择归并排序、计数排序、桶排序或基数排序
-
内存受限:选择堆排序、选择排序或插入排序
-
数据基本有序:插入排序性能接近O(n)
-
数据范围小且为整数:计数排序或基数排序
-
数据分布均匀:桶排序
每种排序算法都有其独特的优势和适用场景,在实际应用中应根据数据规模、数据特性、内存限制和稳定性要求等因素综合选择。