最近被实验室任务和课程大作业压垮了,几乎没时间写博客(恼),为了证明自己没死就把原来计划的文章篇幅砍半先更新出来了......
为了方便知识体系的系统性构建与扩展,机器人学(Robotics)系列将细分为多个子模块,包括运动学与动力学、感知、规划、控制等任何Robotics或偏Robotics的方面,总之博主对自己博客系列的追求就是"大而美"吧......
齐次变换矩阵
机器人操作的定义是指通过某种机构使零件和工具在空间中运动,为此我们需要表达零件、工具以及机构本身的位置和姿态,其包括三个基本问题:
- 如何描述一个物体在空间中的位姿;
- 如何在不同的参照物下描述一个物体的位姿;
- 如何描述一个物体在空间中的运动。
这三个问题分别对应着位姿描述、变换映射和变换算子,它们可以统一由齐次变换矩阵表示。
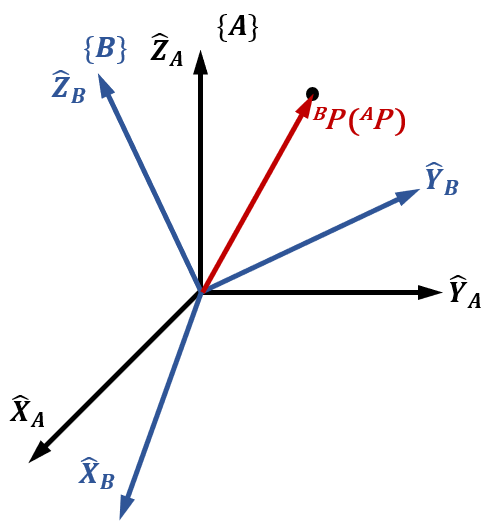
我们采用世界坐标系 (World Frame)作为讨论任何问题的基本参照。一个坐标系{A}\{A\}{A}用三个相互正交的单位矢量X^A,Y^A,Z^A\hat X_A,\hat Y_A,\hat Z_AX^A,Y^A,Z^A来表示。
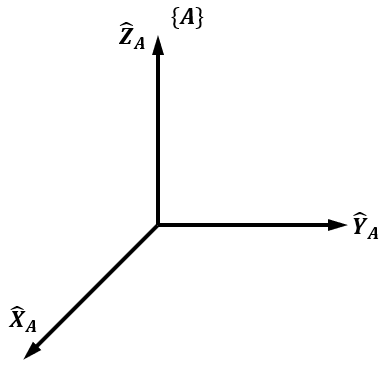
位姿描述
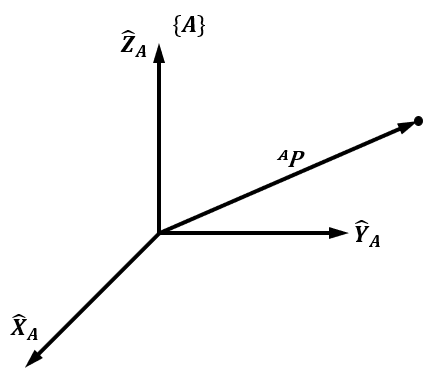
位置 (Position)表示物体在空间中的坐标。世界坐标系中任何点的位置都可以由一个3×13\times13×1的位置矢量 来描述。我们用AP^APAP表示点PPP在{A}\{A\}{A}下的位置矢量
AP=[pxpypz] ^AP=\begin{bmatrix}p_x\\p_y\\p_z\end{bmatrix} AP= pxpypz
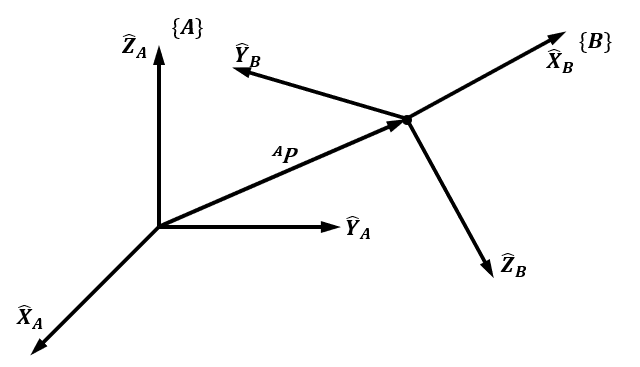
姿态 (Orientation)表示物体的旋转状态或朝向。为了描述物体的姿态,我们需要在物体上固定一个坐标系,并且给出此坐标系相对于参考坐标系的描述。假设固定在物体上的坐标系为{B}\{B\}{B},其主轴方向的单位矢量为X^B,Y^B,Z^B\hat X_B,\hat Y_B,\hat Z_BX^B,Y^B,Z^B,则以{A}\{A\}{A}为参考坐标系描述{B}\{B\}{B}最基本的方法为给出{B}\{B\}{B}的主轴单位矢量在坐标系{A}\{A\}{A}下的表示AX^B,AY^B,AZ^B^A\hat X_B,^A\hat Y_B,^A\hat Z_BAX^B,AY^B,AZ^B。将AX^B,AY^B,AZ^B^A\hat X_B,^A\hat Y_B,^A\hat Z_BAX^B,AY^B,AZ^B按顺序排列可以得到一个3×33\times33×3的矩阵,我们称之为旋转矩阵 (Rotation Matrix)。{B}\{B\}{B}相对于{A}\{A\}{A}的旋转矩阵用BAR^A_BRBAR表示
BAR=(AX^BAY^BAZ^B)=[r11r12r13r21r22r23r31r32r33] ^A_BR=(^A\hat X_B{^A\hat Y_B}{^A\hat Z_B})=\begin{bmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{bmatrix} BAR=(AX^BAY^BAZ^B)= r11r21r31r12r22r32r13r23r33
一个矢量的坐标是其在对应坐标系主轴单位矢量上的投影分量,因此BAR^A_BRBAR中的每个元素也可用{B}\{B\}{B}和{A}\{A\}{A}主轴单位矢量的点积表示
BAR=(AX^BAY^BAZ^B)=[X^B⋅X^AY^B⋅X^AZ^B⋅X^AX^B⋅Y^AY^B⋅Y^AZ^B⋅Y^AX^B⋅Z^AY^B⋅Z^AZ^B⋅Z^A] ^A_BR=(^A\hat X_B{^A\hat Y_B}{^A\hat Z_B})=\begin{bmatrix}\hat X_B\cdot\hat X_A&\hat Y_B\cdot\hat X_A&\hat Z_B\cdot\hat X_A\\\hat X_B\cdot\hat Y_A&\hat Y_B\cdot\hat Y_A&\hat Z_B\cdot\hat Y_A\\\hat X_B\cdot\hat Z_A&\hat Y_B\cdot\hat Z_A&\hat Z_B\cdot\hat Z_A\end{bmatrix} BAR=(AX^BAY^BAZ^B)= X^B⋅X^AX^B⋅Y^AX^B⋅Z^AY^B⋅X^AY^B⋅Y^AY^B⋅Z^AZ^B⋅X^AZ^B⋅Y^AZ^B⋅Z^A
进一步观察上式,可以发现BAR^A_BRBAR的行是{A}\{A\}{A}的主轴单位矢量在{B}\{B\}{B}中的表达,因此BAR^A_BRBAR和ABR^B_ARABR之间互为转置
BAR=(AX^BAY^BAZ^B)=[BX^ATBY^ATBZ^AT]=ABRT ^A_BR=(^A\hat X_B{^A\hat Y_B}{^A\hat Z_B})=\begin{bmatrix}^B\hat X_A^T\\^B\hat Y_A^T\\^B\hat Z_A^T\end{bmatrix}={^B_AR}^T BAR=(AX^BAY^BAZ^B)= BX^ATBY^ATBZ^AT =ABRT
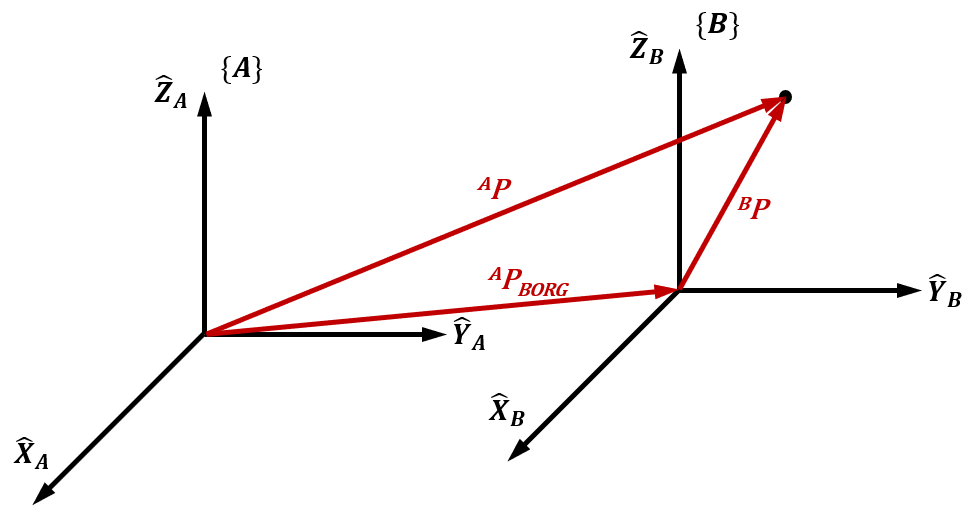
位置和姿态的组合称作位姿 (Pose)。我们在物体上任选一点来描述其位置,并将其作为物体坐标系的原点。{B}\{B\}{B}相对于{A}\{A\}{A}的位姿由旋转矩阵BAR^A_BRBAR及其原点在{A}\{A\}{A}下的位置矢量APBORG^AP_{BORG}APBORG组成(下标ORG表示原点(Origin))
{B}={BAR,APBORG} \{B\}=\{^A_BR,{^AP_{BORG}}\} {B}={BAR,APBORG}
变换映射
将矢量描述从一个坐标系的描述转换到另一个坐标系的描述被称为映射(Mapping)。
当{A}\{A\}{A}与{B}\{B\}{B}的姿态相同,原点位置不同时,可以根据矢量加法由BP^BPBP得到AP^APAP
AP=BP+APBORG ^AP={^BP}+{^AP_{BORG}} AP=BP+APBORG
当{A}\{A\}{A}与{B}\{B\}{B}的原点位置相同,姿态不同时,AP^APAP的每个分量即BP^BPBP在{A}\{A\}{A}的每个主轴单位矢量上的投影
Apx=BX^A⋅BPApy=BY^A⋅BPApz=BZ^A⋅BP \begin{split} ^Ap_x={^B\hat X_A}\cdot{^BP}\\ ^Ap_y={^B\hat Y_A}\cdot{^BP}\\ ^Ap_z={^B\hat Z_A}\cdot{^BP}\\ \end{split} Apx=BX^A⋅BPApy=BY^A⋅BPApz=BZ^A⋅BP
由于旋转矩阵BAR^A_BRBAR的每一行正是BX^A,BY^A,BZ^A^B\hat X_A,{^B\hat Y_A},{^B\hat Z_A}BX^A,BY^A,BZ^A,因此上式可写成矩阵相乘的简化形式
AP=BARBP ^AP={^A_BR}{^BP} AP=BARBP
当{A}\{A\}{A}与{B}\{B\}{B}的原点位置和姿态都不相同时,我们可以引入一个中间坐标系{B′}\{B'\}{B′}。{B′}\{B'\}{B′}由{B}\{B\}{B}绕自身原点旋转到与{A}\{A\}{A}相同的姿态得到。

现在我们可以先将BP^BPBP通过旋转变换表示为B′P^{B'}PB′P,再通过平移变换表示为AP^APAP
B′P=BARBPAP=B′P+APBORG=BARBP+APBORG \begin{split} ^{B'}P&={^A_BR}{^BP}\\ ^AP&={^{B'}P}+{^AP_{BORG}}\\ &={^A_BR}{^BP}+{^AP_{BORG}} \end{split} B′PAP=BARBP=B′P+APBORG=BARBP+APBORG
上式能够表示将一个矢量描述从一个坐标系变换到另一个坐标系的一般变换映射,我们同样可以利用矩阵对其进行简化
AP1\]=\[BARAPBORG0T1\]⏟BAT\[BP1\] \\begin{bmatrix}\^AP\\\\1\\end{bmatrix}=\\underset{\^A_BT}{\\underbrace{\\begin{bmatrix}\^A_BR\&\^AP_{BORG}\\\\\\mathbf{0}\^T\&1\\end{bmatrix}}}\\begin{bmatrix}\^BP\\\\1\\end{bmatrix} \[AP1\]=BAT \[BAR0TAPBORG1\]\[BP1
其中0T\mathbf 0^T0T是一个三维零向量。BAT^A_BTBAT是{B}\{B\}{B}相对于{A}\{A\}{A}的齐次变换矩阵 (Homogeneous Transformation Matrix),它完整地定义了由{B}\{B\}{B}到{A}\{A\}{A}的一般变换映射。在计算过程中我们可以省略第四行的元素,将其简写为以下形式
AP=BATAP ^AP={^A_BT}{^AP} AP=BATAP
变换算子
用于对点或矢量进行移动或旋转的矩阵称为算子(Operator)。
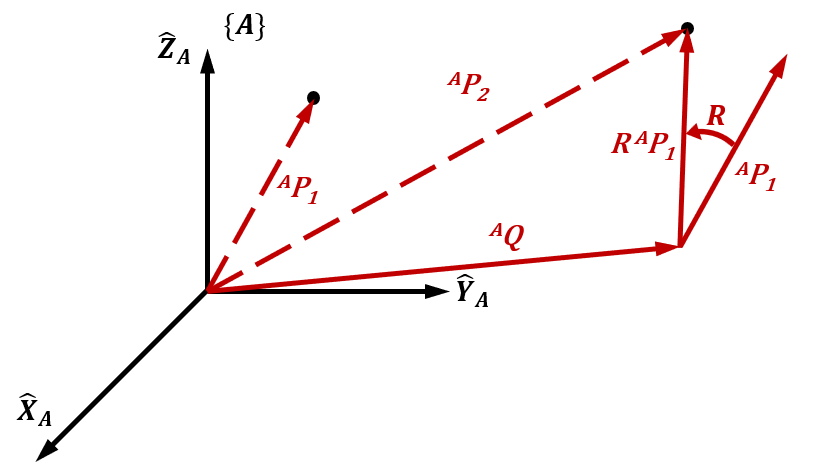
平移算子 将空间中的一个点沿着一个已知的矢量方向移动一定距离。假如位置矢量为AP2^AP_2AP2的点由位置矢量为AP1^AP_1AP1的点通过矢量AQ^AQAQ进行平移得到,则AP2^AP_2AP2计算如下
AP2=AP1+AQ ^AP_2={^AP_1}+{^AQ} AP2=AP1+AQ

用矩阵算子写出上述平移变换,有
AP2=DQ(q)AP1 ^AP_2=D_Q(q){^AP_1} AP2=DQ(q)AP1
其中qqq是沿单位矢量Q^\hat QQ^方向平移的数量,即AQ=qQ^^AQ=q\hat QAQ=qQ^。而算子DQ(q)D_Q(q)DQ(q)则将该平移表示为齐次变换形式
DQ(q)=[100qx010qy001qz0001] D_Q(q)=\begin{bmatrix}1&0&0&q_x\\0&1&0&q_y\\0&0&1&q_z\\0&0&0&1\end{bmatrix} DQ(q)= 100001000010qxqyqz1
旋转算子 将一个矢量以坐标系原点为中心旋转。旋转算子可以由旋转矩阵表示,假如AP2^AP_2AP2由AP1^AP_1AP1经旋转RRR得到,若我们同步将坐标系{A}\{A\}{A}旋转到{A′}\{A'\}{A′},则此时
A′P2=AP1 ^{A'}P_2={^AP_1} A′P2=AP1
而我们现在只需根据变换映射,通过旋转矩阵AA′R^{A'}_ARAA′R将A′P2^{A'}P_2A′P2变换到AP2^AP_2AP2即可
AP2=AA′RA′P2=AA′RAP1 ^AP_2={^{A'}_AR}{^{A'}P_2}={^{A'}_AR}{^AP_1} AP2=AA′RA′P2=AA′RAP1

AA′R{^{A'}_AR}AA′R即由AP1^AP_1AP1到AP2^AP_2AP2的旋转算子RRR,其齐次变换形式为
R=[r11r12r130r21r22r230r31r32r3300001] R=\begin{bmatrix}r_{11}&r_{12}&r_{13}&0\\r_{21}&r_{22}&r_{23}&0\\r_{31}&r_{32}&r_{33}&0\\0&0&0&1\end{bmatrix} R= r11r21r310r12r22r320r13r23r3300001
与DQ(q)D_Q(q)DQ(q)类似,为了在算子符号中表征具体的旋转操作,我们将用另一个符号RK(θ)R_K(\theta)RK(θ)定义旋转算子
AP2=RK(θ)AP1 ^AP_2=R_K(\theta){^AP_1} AP2=RK(θ)AP1
RK(θ)R_K(\theta)RK(θ)表示绕K^\hat KK^轴旋转θ\thetaθ角度。对于一般的旋转轴K^\hat KK^,RK(θ)R_K(\theta)RK(θ)的形式较为复杂。而在三维空间中的任意旋转都可以被拆解为绕X^,Y^,Z^\hat X,\hat Y,\hat ZX^,Y^,Z^三个轴的旋转,以X^,Y^,Z^\hat X,\hat Y,\hat ZX^,Y^,Z^为轴的旋转算子则有如下简洁的形式(由于我们将在计算中用到许多三角函数,因此三角函数用对应首字母简记,即sin\sinsin记为sss,cos\coscos记为ccc)
Rx(θ)=[10000cθ−sθ00sθcθ00001] R_x(\theta)=\begin{bmatrix}1&0&0&0\\0&c\theta&-s\theta&0\\0&s\theta&c\theta&0\\0&0&0&1\end{bmatrix} Rx(θ)= 10000cθsθ00−sθcθ00001
Ry(θ)=[cθ0sθ00100−sθ0cθ00001] R_y(\theta)=\begin{bmatrix}c\theta&0&s\theta&0\\0&1&0&0\\-s\theta&0&c\theta&0\\0&0&0&1\end{bmatrix} Ry(θ)= cθ0−sθ00100sθ0cθ00001
Rz(θ)=[cθ−sθ00sθcθ0000100001] R_z(\theta)=\begin{bmatrix}c\theta&-s\theta&0&0\\s\theta&c\theta&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} Rz(θ)= cθsθ00−sθcθ0000100001
(推导方法:直接列写坐标系绕自身X^,Y^,Z^\hat X,\hat Y,\hat ZX^,Y^,Z^旋转后得到的新主轴单位矢量在原坐标系下的坐标,进而得到对应的旋转矩阵)
关于具体的RK(θ)R_K(\theta)RK(θ)形式与绕坐标轴旋转的组合将在下一篇介绍。
与变换映射一样,同时包含平移和旋转变换的算子即一般变换算子,其形式与齐次变换矩阵相同
T=[r11r12r13qxr21r22r23qyr31r32r33qz0001] T=\begin{bmatrix}r_{11}&r_{12}&r_{13}&q_x\\r_{21}&r_{22}&r_{23}&q_y\\r_{31}&r_{32}&r_{33}&q_z\\0&0&0&1\end{bmatrix} T= r11r21r310r12r22r320r13r23r330qxqyqz1
算子TTT将矢量AP1^AP_1AP1平移并旋转得到一个新矢量
AP2=TAP1 ^AP_2=T{^AP_1} AP2=TAP1
至此,我们可以给出齐次变换矩阵的三种解释:
- 位姿描述 :BAT^A_BTBAT表示相对于坐标系{A}\{A\}{A}的坐标系{B}\{B\}{B};
- 变换映射 :BAT^A_BTBAT是映射BP→AP^BP\rightarrow{^AP}BP→AP;
- 变换算子 :TTT将AP1^AP_1AP1变换为AP2^AP_2AP2。
复合变换与逆变换
多个变换的复合可以通过乘法计算。例如已知{C}\{C\}{C}相对于{B}\{B\}{B}的表示CBT^B_CTCBT和{B}\{B\}{B}相对于{A}\{A\}{A}的表示BAT^A_BTBAT,如果需要通过CP^CPCP求AP^APAP,可先将CP^CPCP变换成BP^BPBP再变换成AP^APAP:
BP=CBTCPAP=BATBP=BATCBTCP \begin{split} ^BP&={^B_CT}{^CP}\\ ^AP&={^A_BT}{^BP}={^A_BT}{^B_CT}{^CP} \end{split} BPAP=CBTCP=BATBP=BATCBTCP
由此可定义CAT=BATCBT^A_CT={^A_BT}{^B_CT}CAT=BATCBT。
我们还会需要通过{B}\{B\}{B}相对于{A}\{A\}{A}的表示BAT^A_BTBAT反求{A}\{A\}{A}相对于{B}\{B\}{B}的表示ABT^B_ATABT,即求BAT^A_BTBAT的逆。求解思路是将其拆分为旋转变换和平移变换,即由BAR^A_BRBAR和APBORG^AP_{BORG}APBORG求ABR^B_ARABR和BPAORG^BP_{AORG}BPAORG。
ABR^B_ARABR的计算由旋转矩阵的性质可知
ABR=BART ^B_AR={^A_BR^T} ABR=BART
BPAORG^BP_{AORG}BPAORG则可以由APBORG^AP_{BORG}APBORG到BPBORG^BP_{BORG}BPBORG映射方程间接得到
BPBORG=ABTAPBORG=ABRAPBORG+BPAORG \begin{split} ^BP_{BORG}&={^B_AT}{^AP_{BORG}}\\ &={^B_AR}{^AP_{BORG}}+{^BP_{AORG}}\\ \end{split} BPBORG=ABTAPBORG=ABRAPBORG+BPAORG
其中BPBORG^BP_{BORG}BPBORG即{B}\{B\}{B}的原点相对于{B}\{B\}{B}的坐标,值为零,因而
BPAORG=−ABRAPBORG=−BARTAPBORG \begin{split} ^BP_{AORG}&=-{^B_AR}{^AP_{BORG}}\\ &=-{^A_BR^T}{^AP_{BORG}} \end{split} BPAORG=−ABRAPBORG=−BARTAPBORG
最终我们可以写出ABT^B_ATABT为
ABT=[BART−BARTAPBORG0T1] ^B_AT=\begin{bmatrix}^A_BR^T&-{^A_BR^T}{^AP_{BORG}}\\\mathbf{0}^T&1\end{bmatrix} ABT=[BART0T−BARTAPBORG1]
参考文献
1\] 机器人学导论(第四版)John J. Craig著