永磁同步直线电机（PMLSM）控制器：滑模控制的探索

永磁同步直线电机（PMLSM）的控制器。包含： ①滑模控制器采用超螺旋法（STA---SMC）②一个传统的滑模算法（SMC）直线电机直线电机直线电机

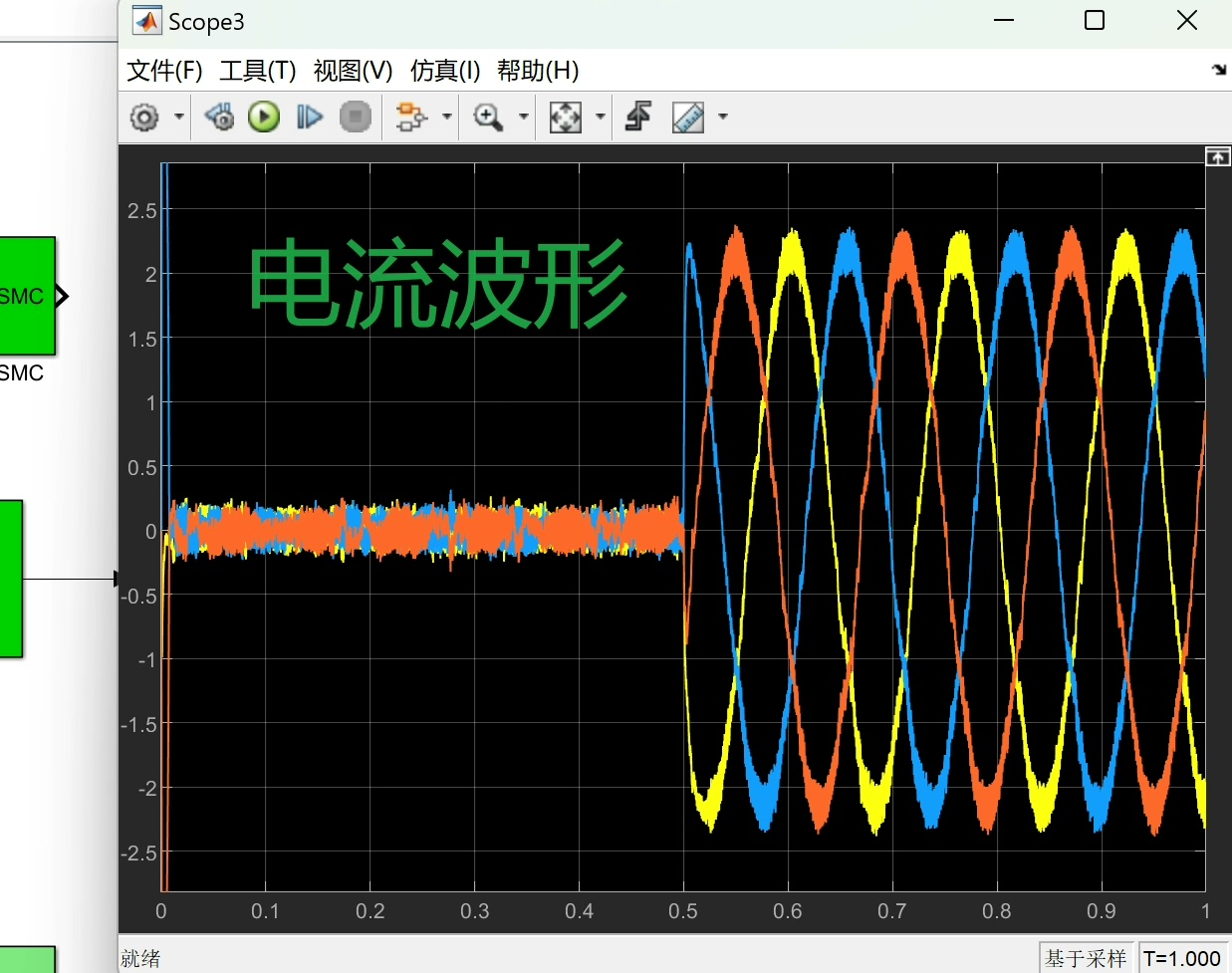
在永磁同步直线电机（PMLSM）的控制领域，滑模控制因其独特的优势而备受关注。今天咱们就来聊聊其中的两种滑模控制算法，传统的滑模算法（SMC）以及超螺旋法（STA - SMC）。

传统滑模算法（SMC）

传统的滑模控制（SMC）是一种变结构控制策略，它通过在系统状态到达滑模面后，迫使系统沿着滑模面滑动，从而实现对系统的有效控制。

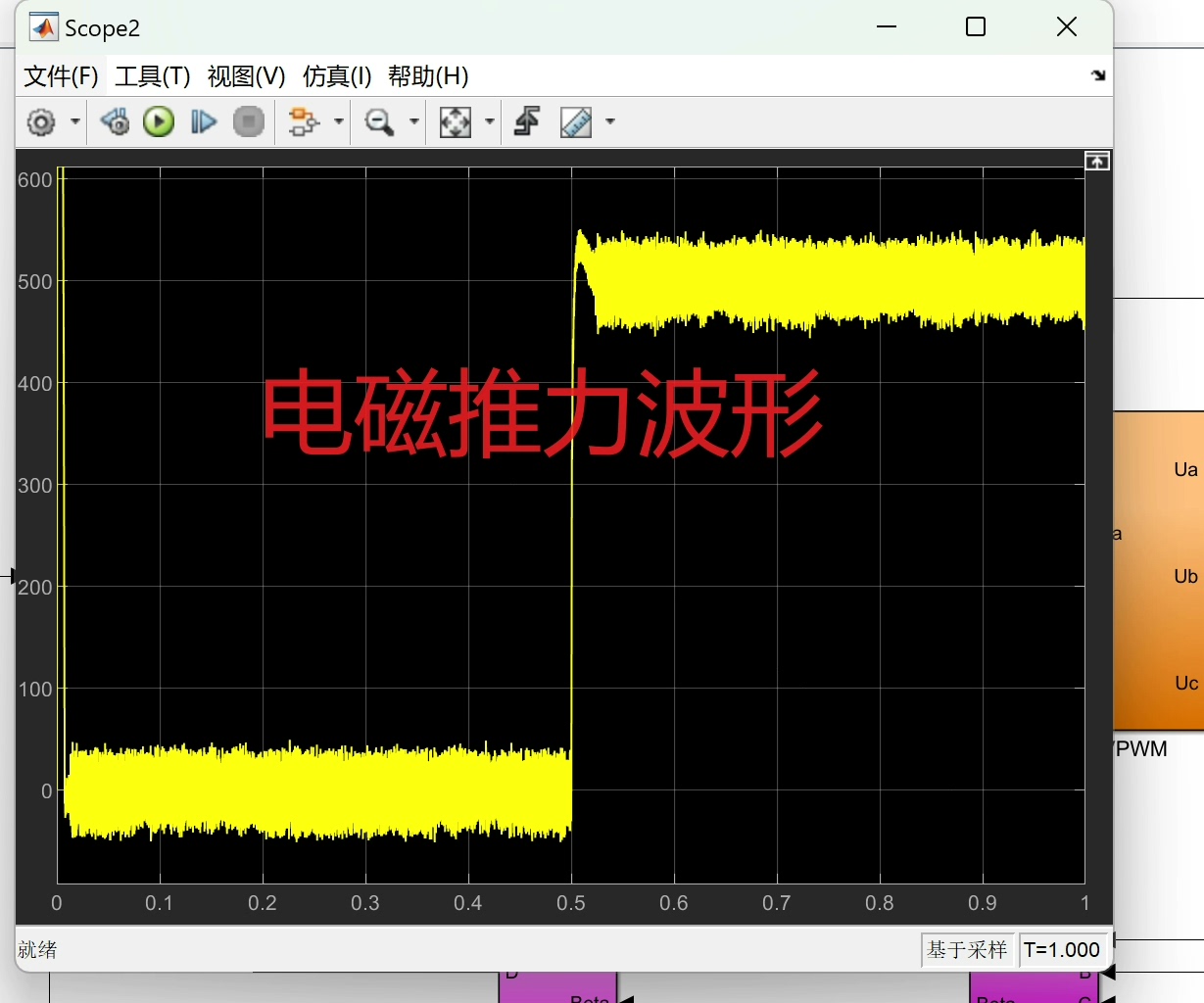
咱们来看看简单的代码示例（以Python为例，这里只是为了示意控制逻辑）：

python 复制代码

import numpy as np

# 系统参数设置
kp = 0.5
kd = 0.3
# 初始状态
x = np.array([0, 0])
# 目标状态
xd = np.array([1, 1])
# 滑模面系数
lambda_s = 1

def smc_control(x, xd):
    e = x - xd
    s = lambda_s * e[0] + e[1]
    if s > 0:
        u = -kp * np.sign(s) - kd * s
    else:
        u = kp * np.sign(s) - kd * s
    return u

在这段代码里，首先定义了系统参数 kp（比例系数）和 kd（微分系数），还有初始状态 x 和目标状态 xd 。smc_control 函数实现了滑模控制的核心逻辑。计算出状态误差 e 后，构建滑模面 s ，然后根据滑模面 s 的值来决定控制输入 u 。当 s 大于 0 时，采用一种控制策略，小于 0 时则采用另一种，通过这种切换来迫使系统状态趋向滑模面并沿着其滑动。

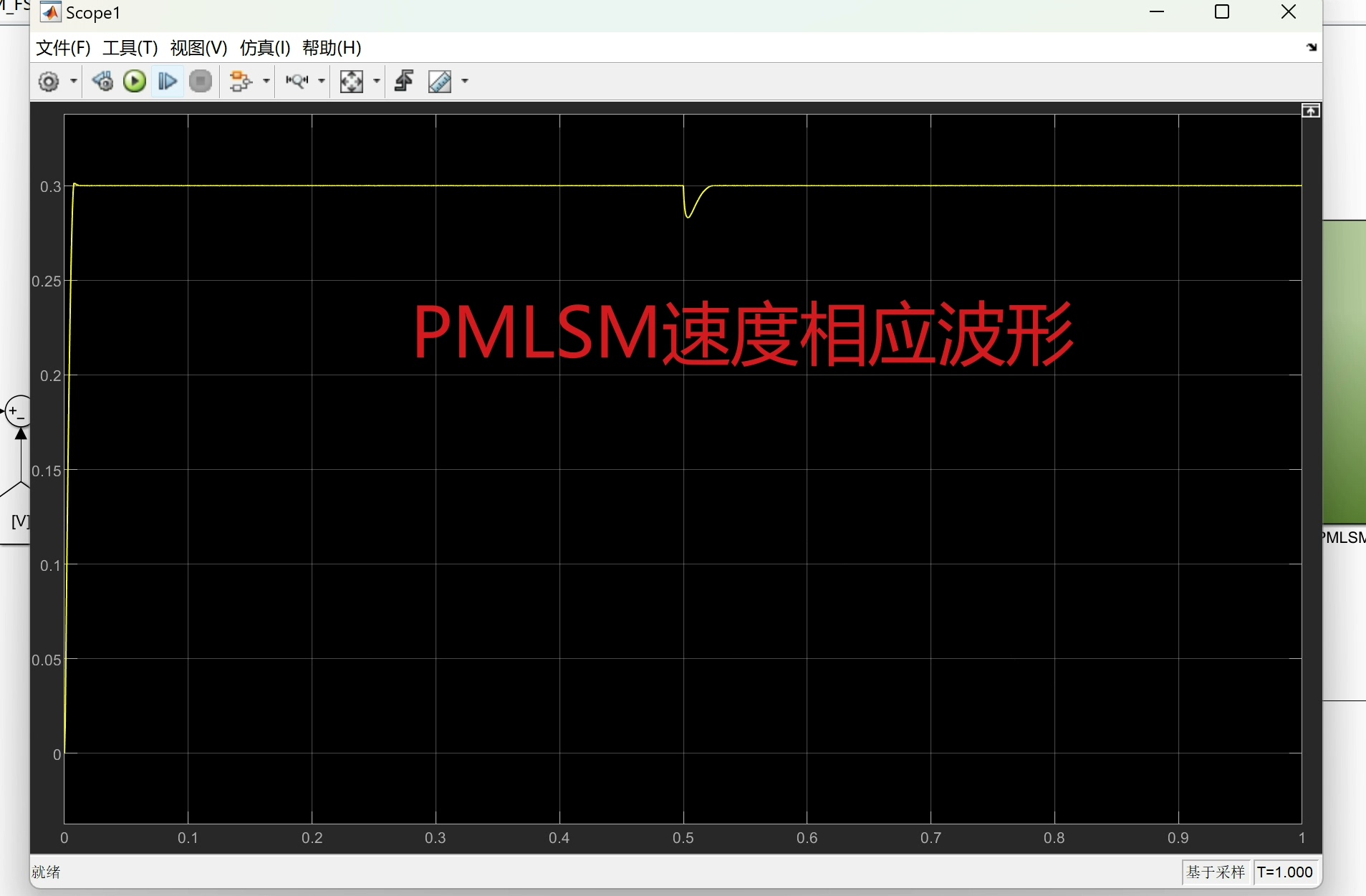
不过传统的SMC也有个小毛病，就是控制输入的高频切换会导致抖振现象，这对系统的实际运行可不太友好。

超螺旋法（STA - SMC）

超螺旋法（STA - SMC）就是为了解决传统SMC的抖振问题而诞生的。它通过引入积分项等方式，实现了连续的滑模控制，有效削弱了抖振。

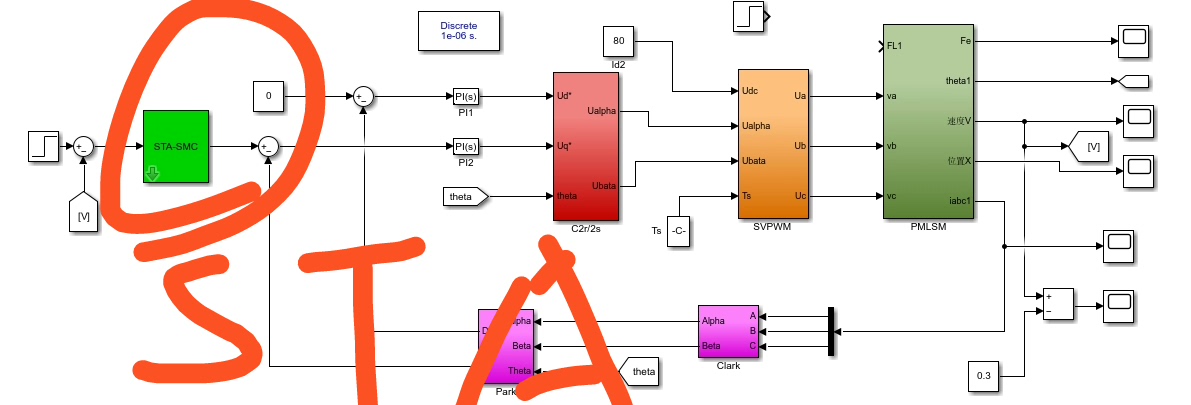
同样来看代码示例：

python 复制代码

import numpy as np

# 系统参数设置
alpha = 1.5
beta = 1
# 初始状态
x = np.array([0, 0])
# 目标状态
xd = np.array([1, 1])
# 初始化积分项
z = 0

def sta_smc_control(x, xd, z):
    e = x - xd
    s = e[0]
    u1 = -beta * np.abs(s) ** 0.5 * np.sign(s)
    z_dot = -alpha * np.sign(s)
    z = z + z_dot
    u = u1 + z
    return u, z

在这个STA - SMC的代码实现中，定义了参数 alpha 和 beta 。stasmccontrol 函数里，先计算状态误差 e ，构建滑模面 s 。这里控制输入 u 由两部分组成，u1 是和滑模面相关的一项，通过积分项 z 不断更新，最终组合成总的控制输入 u 。这种方式使得控制输入更加平滑，大大减轻了抖振现象，让永磁同步直线电机（PMLSM）能够更加稳定地运行。

通过对传统滑模算法（SMC）和超螺旋法（STA - SMC）在永磁同步直线电机（PMLSM）控制中的探讨，我们可以看到不同滑模控制策略的特点和优劣，这对于我们根据实际需求选择合适的控制算法提供了很好的参考。希望这些内容能给正在研究直线电机控制的小伙伴们一些启发！