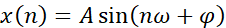
正弦序列的由来是对连续时间信号进行等间隔T的采样，得到正弦序列！
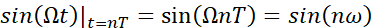
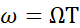
其中，ω 为数字角频率 rad ，Ω 为模拟角频率rad/s ，T为采样间隔，两个采样点之间间隔多少秒。模拟角频率Ω 是指信号每秒相位的变化，数字角频率ω 乘上了采样间隔T，指的是信号每个采样点相位的变化！也就是序列的最小单位是采样点，类别于模拟信号的秒。
举个例子：
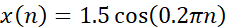
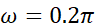
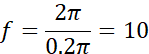
显然，数字角频率ω =0.2π ，也就是一个采样点相位变化了0.2π ，频率f=10 ，表示一个周期需要10个采样点！
对长度为N 的序列 xn 进行离散傅里叶变换，可以得到长度同样为N的复数Xk ！其中，0≤k≤N-1 。Xk 的物理意义是第k 个离散频率点 fk 上的复频谱系数：
注意**，这里的** k 是从 0 开始的，也就是 Xk 的第一个值是直流量！ Xk 可以表示为幅度和相角的形式。
其中，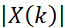
和频率为fk 的余弦函数的幅值A 的关系如下，具体的推导可以去看《对FFT输出结果的影响》信号分析（一）------FFT输出结果是什么？_fft变换出来直接是双边谱吗-CSDN博客
φ 是频率为fk 的余弦函数的相角，这里的谐波统一为余弦函数！