一、 问题定义与优化目标
- 工件材料: 440C不锈钢
特性: 高碳马氏体不锈钢,高硬度(HRC 58-60),高耐磨性,但导热性差,磨削时易产生:
磨削烧伤(热损伤)
残余拉应力
表面/亚表面微裂纹
轮毂堵塞
核心矛盾: 提高材料去除率(效率)与保证加工表面完整性(质量)之间的冲突。
- 关键磨削参数(输入变量)
工件速度 (Vw): rpm 或 m/min
砂轮线速度 (Vs): m/s
径向进给量/切深 (ap): mm/pass 或 µm
轴向进给速度 (f): mm/rev 或 mm/min
- 优化目标(输出响应)
通常为多目标,需同时优化:
目标1(质量 - 最小化): 表面粗糙度 - 衡量表面光洁度。
目标2(质量 - 最小化): 残余应力/或烧伤程度 - 衡量亚表面损伤。可用白光干涉仪、X射线衍射仪测量,或通过监测声发射、温度间接表征。
目标3(效率 - 最大化): 材料去除率 - 衡量加工效率。
- 约束条件
磨削温度 ≤ 材料相变临界温度(避免烧伤)
砂轮磨损在合理范围内
机床功率与刚度限制
表面粗糙度Ra ≤ 指定值(如Ra 0.4µm)三、 详细实施步骤
二、 详细实施步骤
阶段一:基于RSM的实验设计与建模
确定因素与水平: 基于预实验和文献,为四个关键参数(Vs, Vw, ap, f)确定合理的高低水平。
选择实验设计: 采用中心复合设计(CCD),它能高效地拟合二阶响应曲面模型。对于4因子,CCD通常需要约30次实验(包括中心点重复和轴向点)。
进行实验: 在精密外圆磨床上,按CCD设计的参数组合进行磨削实验。严格控制冷却液、砂轮修整等其他条件。
测量响应: 对每个实验样本测量表面粗糙度(Ra)、残余应力(或使用红外测温/声发射传感器间接监测热损伤信号),并计算材料去除率。
构建RSM模型: 使用最小二乘法拟合二阶多项式模型。例如,对于表面粗糙度Ra:
Ra = β₀ + ΣβᵢXᵢ + ΣβᵢⱼXᵢXⱼ + ΣβᵢᵢXᵢ² + ε
其中,Xᵢ 为编码后的磨削参数,β为回归系数。
模型验证: 进行方差分析(ANOVA),检查模型的显著性(P值<0.05)、失拟项和决定系数R²(通常>0.9)。若不满足,需考虑增加实验或引入更高阶模型。
阶段二:基于MOGWO的多目标优化
问题公式化:
决策变量: Vs, Vw, ap, f(编码值或实际值)。
目标函数:
Minimize: [f₁(Ra), f₂(热损伤指标), -f₃(MRR)]
。注意MRR需转换为最小化问题(即最大化MRR等价于最小化 -MRR)。
约束条件: 将模型预测值代入约束不等式(如 Ra ≤ 0.4, 温度 ≤ T_critical)。
MOGWO算法流程集成:
初始化狼群: 在参数可行域内随机生成一组灰狼(即参数组合)。
适应度评估: 对每只狼(每个参数组合),代入已建立的RSM模型,快速计算其对应的Ra、热损伤指标和MRR的预测值。这是RSM为MOGWO提供的高速、低成本"代理模型",避免了每次评估都进行耗时耗材的真实实验。
非支配排序与归档: 根据多目标适应度,对狼群进行帕累托支配关系排序,并更新外部归档集(储存当前找到的帕累托最优解)。
领导狼选择: 从归档集中选择三个最优解作为α、β、δ狼,引导种群更新。
位置更新: 模拟包围、狩猎等行为,更新灰狼位置(即探索新的参数组合)。
迭代: 重复评估、排序、更新步骤,直至达到最大迭代次数。
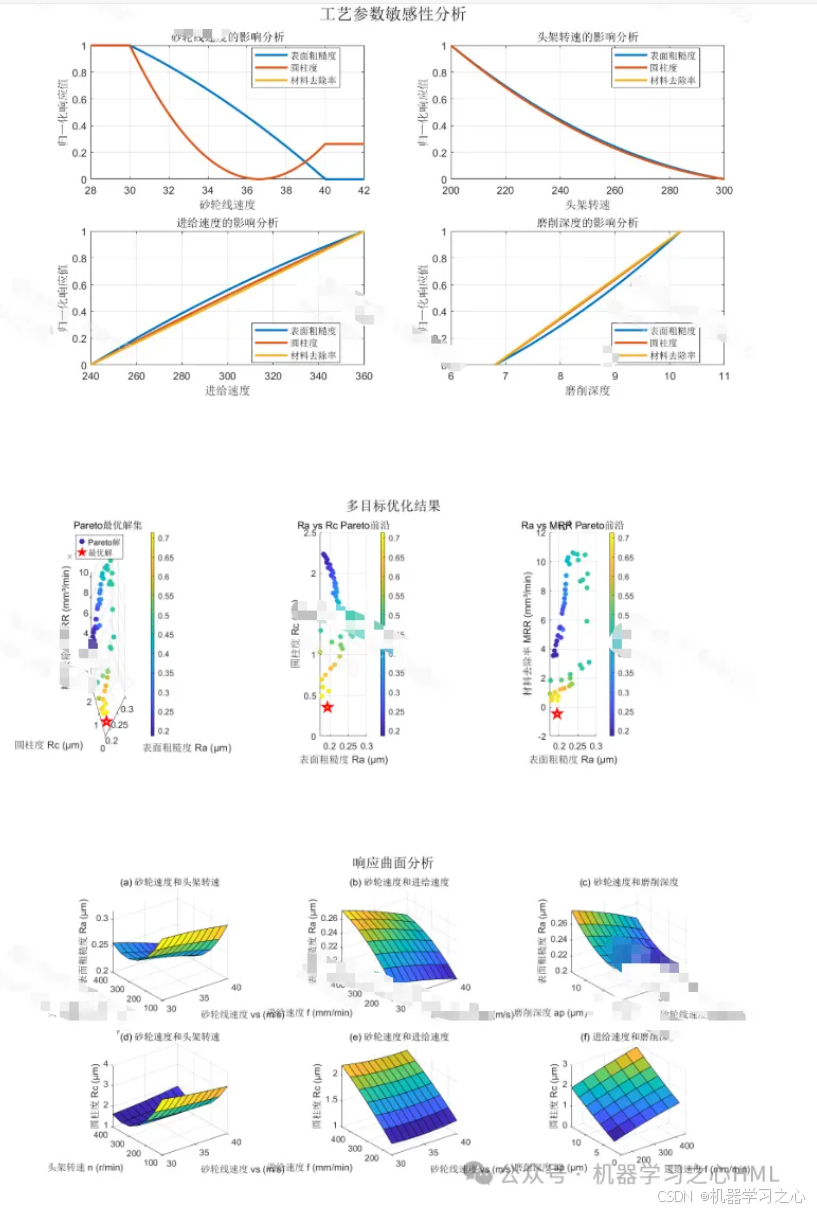
输出: 最终的外部归档集即为帕累托最优前沿------一组在多个目标间最佳折衷的参数解集。
阶段三:最优决策与实验验证
从帕累托前沿中决策: 根据实际生产偏好(例如,更侧重质量还是效率),使用TOPSIS、模糊决策等方法,从众多非支配解中选择一个"最佳折衷解"。
验证实验: 用决策出的最优参数组合进行验证性磨削实验,测量实际响应值。
对比分析: 将实测值与RSM-MOGWO的预测值对比,计算误差。若误差在可接受范围内(如<10%),则证明优化系统有效。
三、 总结
基于RSM和MOGWO的优化策略,为440C不锈钢外圆磨削工艺提供了一条"数据驱动"的智能化路径。 它首先通过RSM从实验数据中"学习"工艺规律,建立定量预测模型;然后利用MOGWO在这个模型构成的高维目标空间中,智能搜索全局最优的工艺参数组合。这套方法学具有通用性,可推广至其他硬脆材料的高性能磨削工艺开发中。