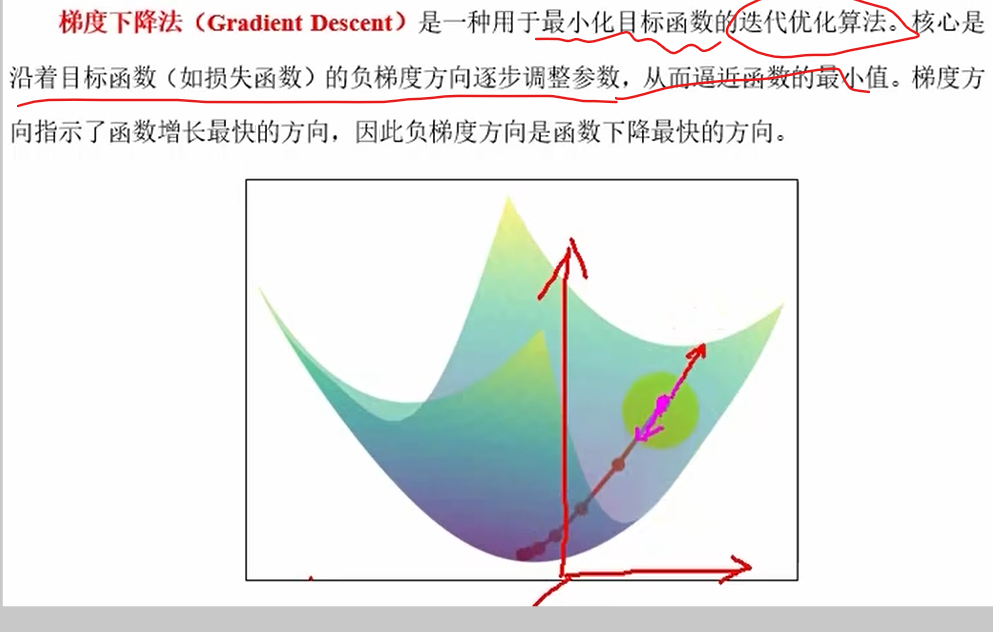
损失函数

常见损失函数
MSE均方误差
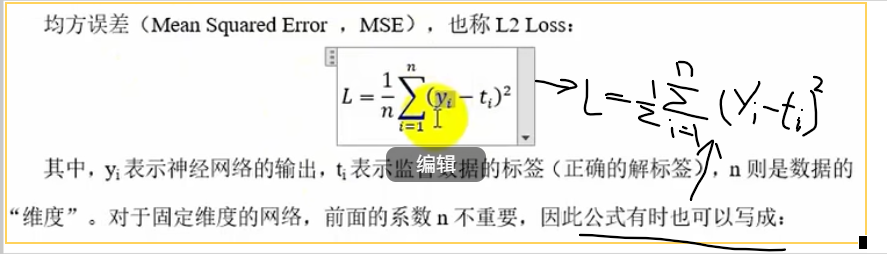
多用于回归,1/2求导用
L2 loss对异常值敏感,遇到异常值会发生梯度爆炸(求导时平方会将小的变更小,大的变更大)
# MSE y预测值,t真实值
# y,t n*1
def mean_squared_error(y,t):
return np.sum((y-t)**2)/2CEE交叉熵误差

下列代码输入y和t:
y(n*k):n个样本可能是k个类
t:有两种输入,若是(n*k)则是独热编码(one-hot)一行中除了最大概率为1,其他全为0
若是(n*1)则是顺序编码,存储每个样本对应的最大值概率的索引
# 交叉熵误差CEE
def cross_entropy(y,t):
# 若只有一个样本,将y转为二维
if y.ndim==1:
t=t.reshape(1,t.size)
y=y.reshape(1,y.size)
# 将t转化为顺序编码(类别标签)
if t.size==y.size: # t.size是所有维度乘积,若y和t维度一样,说明t是独热编码表达
t=t.argmax(axis=1) # 找出二维数组中跨列最大值对应的索引
n=y.shape[0]
'''
y[np.arange(n),t]是花式索引
他不是找所有行,所有t列的数据
而是找[1,2,..,n]行分别对应的t=(1,6,8,7..)'列的n个元素
t必须是一维n个数的索引数组
y[np.arange(n),t]:n*1
+1e-10 : 加一个微小误差,防止log计算=0
'''
return -np.sum(np.log(y[np.arange(n),t]+1e-10))分类损失函数
二分类交叉熵损失函数


多分类交叉熵损失函数

回归损失函数
MAE
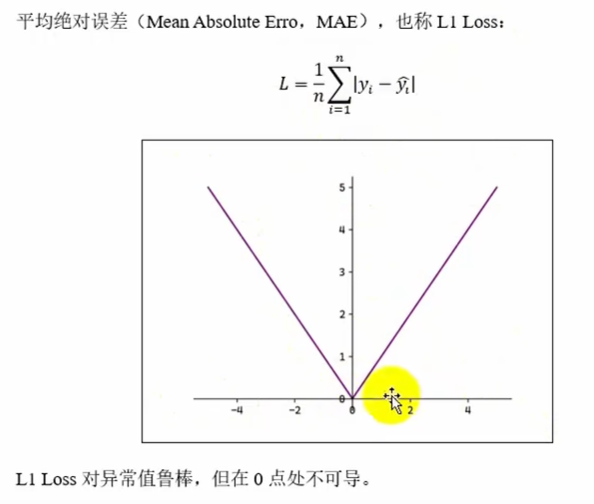
MSE
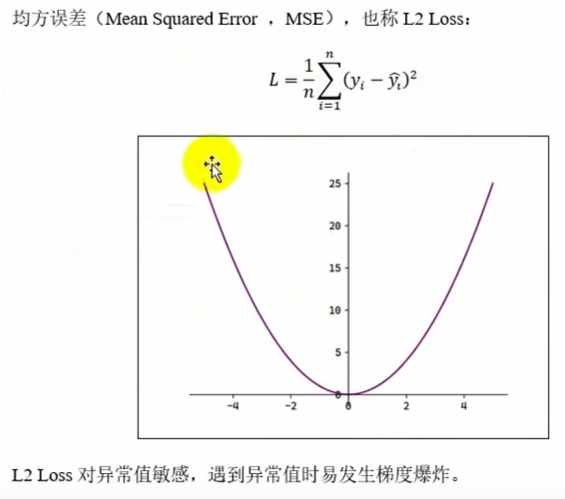
smooth L1
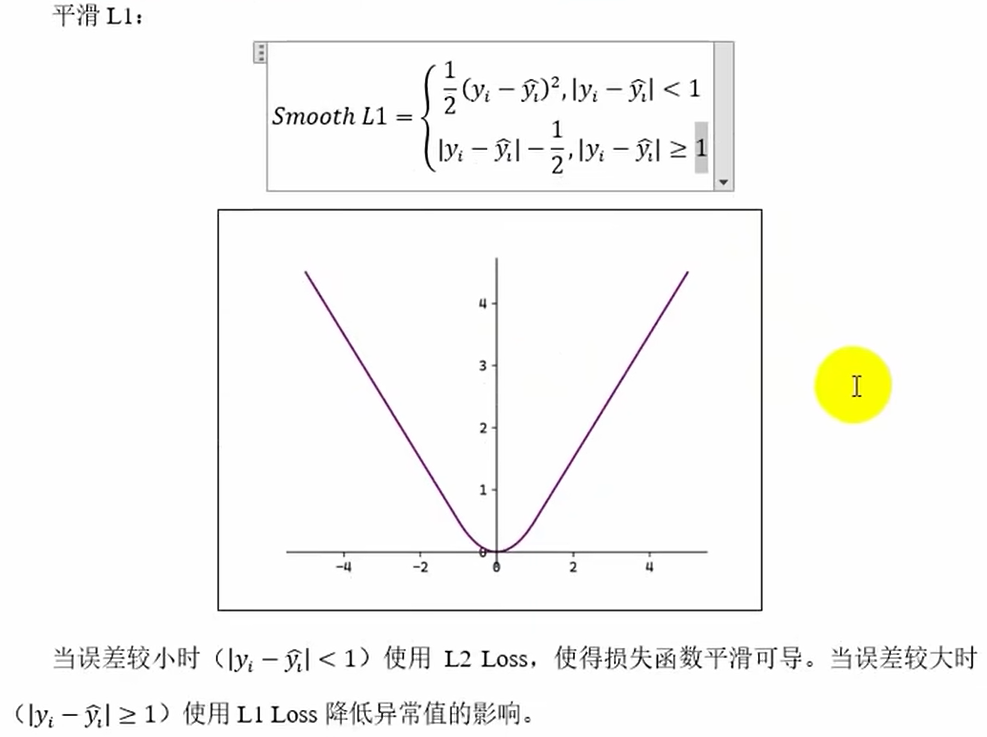
数值微分
数值微分求导
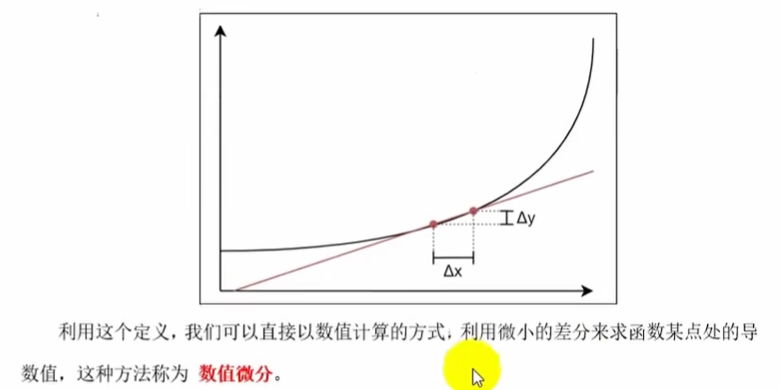
# 数值微分求导
def numerical_diff(f,x):
h=1e-4
return (f(x+h)-f(x-h))/(2*h)就是线性拟合
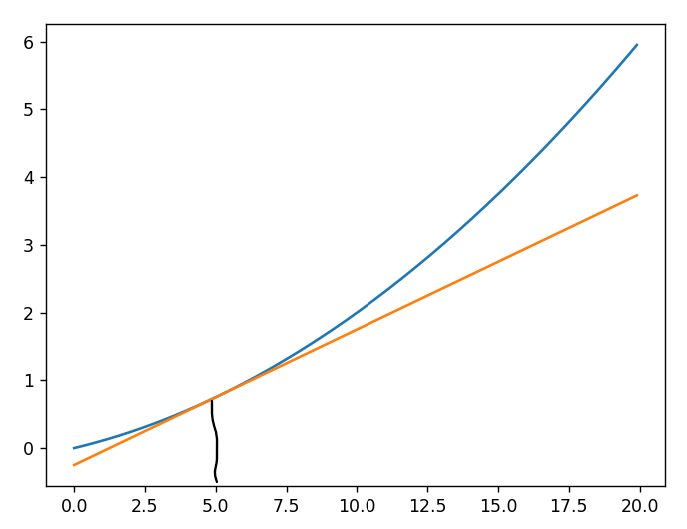
计算x点拟合切线
原函数y=0.01x^2+0.1x
import numpy as np
import matplotlib.pyplot as plt
from common.gradient import numerical_diff
# 设原函数y=0.01x^2+0.1x
def f(x):
return 0.01*x**2+0.1*x
# 切线方程函数,返回切线函数
def tangent_line(f,x):
y=f(x)
# 计算x处切线的斜率(利用数值微分计算x处导数)
a=numerical_diff(f,x)
b=y-a*x
return lambda x:a*x+b
# 定义画图范围
x=np.arange(0.0,20.0,0.1)
y=f(x)
# 计算x=5处切线方程,f_line是匿名函数
f_line=tangent_line(f,x=5)
y_line=f_line(x)
plt.plot(x,y) # 原函数曲线
plt.plot(x,y_line) # 切线
plt.show()运行结果:
计算梯度
import numpy as np
# 数值微分求导
def numerical_diff(f,x):
h=1e-4
return (f(x+h)-f(x-h))/(2*h)
# 数值微分求梯度,传入的x是一个向量
def _numerical_gradient(f,x):
h=1e-4
grad=np.zeros_like(x)
# 遍历x中的特征xi
for i in range(x.size):
temp=x[i]
x[i]=temp+h
fxh1=f(x)
x[i]=temp-h
fxh2=f(x) # 传的是x[i],or f(x[i])
# 利用中心差分公式计算偏导数
grad[i]=(fxh1-fxh2)/(2*h)
x[i]=temp
return grad
# 传入X是一个矩阵
def numerical_gradient(f,X):
# 判断维度
if X.ndim==1:
return _numerical_gradient(f,X)
else:
grad=np.zeros_like(X)
# 遍历X中的每一行数据,分别求梯度
for i,x in enumerate(X):
grad[i]=_numerical_gradient(f,x) # 这里grad[i]就是一个向量
return grad神经网络的梯度计算
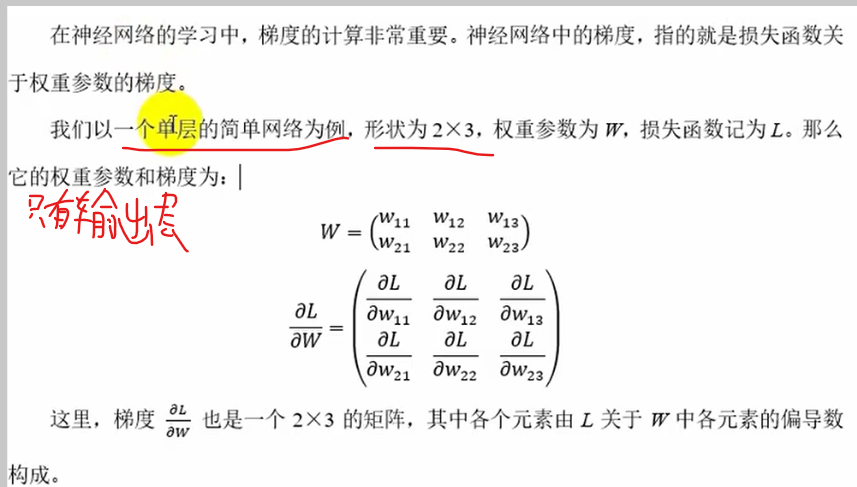
import numpy as np
from common.functions import softmax,cross_entropy
from common.gradient import numerical_gradient
# 定义一个简单神经网络类
class SimpleNet:
def __init__(self):
#输入2,输出3
self.W=np.random.randn(2,3)
# 前向传播
def forward(self,X):
a=X@ self.W # 没写偏置值
y=softmax(a)
return y # 1*3
# 计算损失值
def loss(self,x,t): # t是真实y
y=self.forward(x) # 预测y
loss=cross_entropy(y,t) # 求y用到了self.W
return loss
# 主程序
if __name__=='__main__' :
# 1.定义数据
x=np.array([0.6,0.9])
t=np.array([0,0,1]) # 独热编码
# 2.定义神经网络模型
net=SimpleNet()
# 3.计算梯度
f=lambda w:net.loss(x,t)
# 传入的f是运算逻辑,且lambda w: net.loss(x, t) 并没有使用传入的 w,
# f真正参数是net.W
gradw=numerical_gradient(f,net.W)
print(gradw)运行结果:
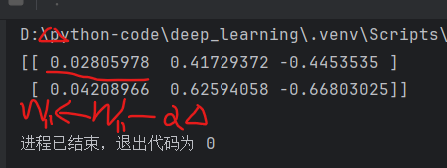
随机梯度下降法(SGD)
梯度下降法